The Power to Tax: Analytical Foundations of a Fiscal Constitution
By Geoffrey Brennan and James M. Buchanan
Publisher
none
- Foreword
- Ch. 1, Taxation in Constitutional Perspective
- Ch. 2, Natural Government
- Ch. 3, Constraints on Base and Rate Structure
- Ch. 4, The Taxation of Commodities
- Ch. 5, Taxation through Time
- Ch. 6, Money Creation and Taxation
- Ch. 7, The Disposition of Public Revenues
- Ch. 8, The Domain of Politics
- Ch. 9, Open Economy, Federalism, and Taxing Authority
- Ch. 10, Toward Authentic Tax Reform
- Epilogue
- Selected Bibliography
 The Disposition of Public Revenues
The Disposition of Public Revenues
**
Public services are never performed better than when their reward comes only in consequence of their being performed, and is proportional to the diligence in performing them.
—Adam Smith,
The Wealth
of Nations, p. 678
In the analyses of Chapters 3 through 6, we have been concerned primarily with ways in which the constitutional selection of tax institutions might be used to limit the overall
level of governmental activity, the withdrawal of resources from the private sector of the economy. In order to concentrate on this aspect of constitutional fiscal choice, we assumed that the
disposition of governmentally collected revenues was set exogenously, that is, independent of the tax system itself. By “disposition” here we refer to the mix between that share of revenues collected that is devoted directly to the production or provision of goods and services valued by taxpayers-consumers and that share directed to the provision of perquisites (pecuniary and nonpecuniary) to the politicians-bureaucrats. The
disposition of revenues, as defined, is clearly an important element in the efficiency of the fiscal system, an element that is not necessarily less important than the
level of revenues, previously analyzed.
*90 In this chapter, we shall focus primarily on the disposition-of-revenues issue.
The setting for analysis is the same as that introduced in preceding chapters. We are examining the choice calculus of an individual at the constitutional stage where he is confronted with a selection of tax or fiscal instruments that are to be applied throughout a sequence of periods. At this stage, the individual is presumed to be unable to predict what his own economic position will be during the relevant sequence. We presume, further, that the only controls upon the Leviathan-like proclivities of government are those that might be imposed constitutionally. Voters-taxpayers are essentially powerless to affect government’s fiscal activities in postconstitutional political settings.
Previous discussion has demonstrated how the potential taxpayer-beneficiary may seek to build constraints into the effective tax constitution that will limit the total revenue demands of government. But how may the potential taxpayer-beneficiary, at the same time, ensure that the revenues collected will be devoted to the financing of those goods and services that he values? Once given the taxing power, what is to prevent Leviathan from utilizing revenue to further its own particular purposes? At one period in history, monarchs used substantial revenues to equip and maintain lavishly appointed courts;
*91 in more recent times, excessive staff, high salaries, numerous perquisites, and congenial working conditions have characterized governmental establishments.
A variety of mechanisms may, of course, be conceived which might prevent undue diversion of revenues from the intended purpose of providing public services. In this chapter, however, we want to concentrate on those enforcement mechanisms that may be built into the tax structure itself. The particular virtue of tax constraints, as opposed to most of the obvious alternatives, is that they build into the very structure of Leviathan’s coercive power an automatic interest in wielding such power for the “common good”: the incentives are arranged so that the natural appetites of Leviathan are mobilized to ensure that, to a substantial degree, revenues are used as taxpayers desire them to be used. The fiscal constitution becomes, in this basic sense, self-enforcing. The central feature in such a constitution is a particular form of earmarking, which the analysis of this chapter will demonstrate.
7.1. The Model
Because the focus of analysis is somewhat different from that in preceding chapters, it will be useful to restate our basic model. The quantity of the public good (or public-goods bundle),
G, provided by the monopoly government (Leviathan) is defined as
| G = aR, |
(1) |
where, as before,
R is total tax revenue collected and
a is the share or proportion of that revenue devoted to outlay on the public good,
G. In earlier chapters, we examined limits on
R that might be exerted by appropriately chosen constitutional restrictions on tax bases and rate structures, with the value of
a assumed to be exogenously fixed. In such a context, it was appropriate to assign a revenue-maximizing objective to Leviathan (or value-maximizing in the case of inflationary finance). This objective function for a Leviathan government was invariant as between a Niskanen-type bureaucracy model, in which the value of
a is effectively unity, by virtue of constraints inherent in the political process,
*92 and a “pure surplus” model, in which the maximand is the excess of revenues collected over outlays on the public good. The fixity of
a implies revenue maximizing as a rational course of action in either case. [In the “pure surplus” model, the maximand becomes (1 –
a)
R, which for given
a, is maximized simultaneously with
R.]
The restrictive effects of assuming
a to be fixed should be clear. It is evident that the value of
a may depend on the tax institutions selected, and it is this relationship that we address directly in this chapter. Let us suppose that we envisage the constitutional process as one that establishes a “monarchy,” under which a “king” may be treated as a utility maximizer in the standard manner. Both the monarchy and the king here are, of course, artifacts constructed solely for convenience in exposition. The king becomes a shorthand expression for the appropriately chosen collection of politicians and bureaucrats whose behavior generates outcomes in postconstitutional political settings, or even the decisive majority in a context of revolving coalitions where that majority exploits the minority. In any case, this collection acts “as if” it were a utility-maximizing entity, or king.
We ascribe to this behavioral unit the maximand,
Y
k, where
| Y k = R – G, |
(2) |
| Y k = (1 – a) R. |
(3) |
Given (3), the king will aim to maximize
R and to minimize
a (i.e., to set
a at zero) if
R and
a are unrelated. If, however,
a can, in some way, be positively related to
R, the maximization of
Y
k may not involve the minimization of
a. Recognition of this facet of the king’s maximization problem provides the setting for the potential taxpayer-beneficiary’s constitutional strategy in choosing tax instruments to assign to the king in the first place.
Before explaining this strategy in some depth, it is necessary to specify carefully the relationship of the king to other members of the political community. If the goods and services expected to be provided by government,
G, are genuinely “public” in the nonexcludable sense, and, further, if the king shares in the benefits along with others,
a may not be reduced to zero, even if its value remains wholly within the control of the king. That is, if the king’s utility function,
U
k, contains an argument for
G as well as for privately divisible goods that may be enjoyed exclusively, a strict maximizing calculus would imply some provision of
G, and hence some value for
a, assuming the absence of lumpiness. Largely for purposes of simplifying our discussion here, we shall initially assume that the king is wholly external to the other members of the community in the sense that he does not secure any positive benefits from the provision of
G, even though the latter may be described as a collective-consumption good for all other persons. A somewhat more complex model which allows the king to be among the sharers of public-goods benefits and/or which allows for
G as a direct argument in the king’s own utility function is presented in Section 7.4. In Sections 7.2 and 7.3, we shall assume that the king does not benefit from public-goods supply and that the surplus that accrues to the king is pure loss to the society. Both assumptions can be considerably weakened without the central results being lost—but initially it is convenient to deal with the more extreme case.
7.2. Public-Goods Supply under a Pure Surplus Maximizer: Geometric Analysis
The characteristic feature of our Leviathan model is that, in the absence of any constraints that force him to act differently, the king will set
a at zero. That is, he will provide none of the public good,
G, valued by citizens. He will simply maximize tax revenues,
R, and he will utilize all of these for the funding of his own privately consumed goods and services. The question to be posed is as follows: Is there any way in which tax institutions may be selected, at the constitutional stage, so that
a will not be set at zero—so that at least some
G will be provided?
By our Leviathan-like assumptions about political process in postconstitutional periods, the potential taxpayers-beneficiaries have no direct control over the quantity of
G provided by government. How can the king be induced to supply some positive quantity as a part of his own utility-maximizing behavior? Such inducement may be introduced if, by supplying
G, total revenue collections are increased sufficiently to increase
Y
k. That is, an increase in
a, the proportion of revenue devoted to the financing of
G, may, in certain cases, increase the value of (1 –
a)
R, provided that there is a positive relationship between
a and
R.
Total revenues,
R, are a function of the tax base and rate structure. In order to generate the required positive relationship between
R and
a, therefore, the base and rate structure, the essential determinants of
R, must be variable and somehow related to the provision of
G. This suggests that the tax base, whether it be an expenditure item or an item of income, must be
complementary with the provision of
G, as reflected in the independent behavioral adjustments of the taxpayers-beneficiaries.
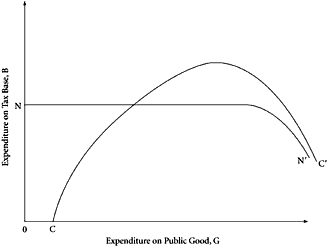 |
| Figure 7.1 |
The tax-base variable,
B, may be arranged so that it is subject to some direct control by the taxpayers-beneficiaries. The public-goods variable,
G, is, by our assumptions, under the direct control of government. Hence, we have a reaction-function sequence that may be illustrated in familiar diagrammatics. In Figure 7.1, we measure
G along the abscissa and
B along the ordinate, both in dollar units. Consider now the curve
NN‘, which is drawn to be horizontal over the range out to some production constraint. This represents the locus of equilibrium consumption levels of
B as the quantity of
G increases or, alternatively, the reaction curve (line of optima, ridge line) traced out by the utility-maximizing reaction of taxpayers-beneficiaries in “supplying”
B for each possible level of
G. Over the relevant range along
NN‘, note that the “supply” of taxable base,
B, is invariant with the provision of
G. In such a situation, the government would have no incentive at all to use any tax revenues collected to provide a positive quantity of
G. It can maximize
R by levying the highest allowable tax rate on
B, and then maximize
Y
k by using all of the
R to satisfy its own strictly private needs.
Contrast this situation with one in which
B is highly complementary with
G. The curve
CC‘ in Figure 7.1 depicts this case. Note that here the amount of taxable base “supplied” by the taxpayers-beneficiaries increases with the amount of
G provided by government, at least over a substantial relevant range. And as
CC‘ in Figure 7.1 suggests, there may be situations where any revenue collection is impossible without some positive provision of the public good: individuals will simply not spend money on
B unless there is some
G to consume with it.
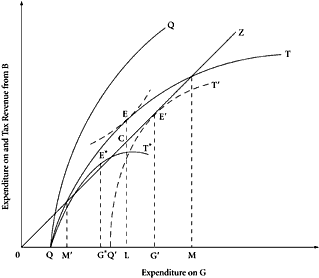 |
| Figure 7.2 |
In order to determine how much
G will be provided, it is necessary to specify the relationship between tax revenues and the tax base. For this purpose, we assume that the government is limited to a specific rate structure—which for ease of treatment we take to be proportional. This allows us, in Figure 7.2, to depict a relationship between the equilibrium amount of
B consumed by individuals and the level of
G, in the presence of the revenue-maximizing proportional tax rate,
t*, applied to the designated base,
B. This is shown by
QQ, which will in general differ from
C‘
C in Figure 7.1. The curve
QQ traces out the behavioral adjustments of taxpayers-beneficiaries in generating taxable base under the imposition of the maximum revenue tax. (
QQ may lie above, below, or be coincident with
CC‘ over any part of the relevant range, with the precise relationship being primarily dependent here on the income elasticity of demand for the base variable.) The curve
QT in Figure 7.2 relates the tax collections derived from the revenue-maximizing tax on
B to levels of
G provision. For each level of
G, the vertical distance from the abscissa to
QT represents total tax revenue. The vertical distance between
QT and
QQ represents net-of-tax expenditures on
B.
On the basis of the set of relationships indicated in Figure 7.2, what level of spending on
G will the surplus-maximizing king opt for? Given that he is restricted to tax base
B and a proportional rate structure, we can answer this question by constructing a 45° ray, 0
Z, from the origin. Since all variables are measured in dollar units, the location of a position on the 45° line implies that all revenues collected from the tax are required for spending on the provision of
G. There is no net surplus. (Here, as elsewhere, we assume that government has no access to revenue-raising instruments other than those being analyzed.) Clearly, if
B is the only tax source available, points to the left of
M‘ are infeasible: the maximum revenue that can be raised from taxing
B cannot, over this initial range, sustain the levels of
G that are required to generate such revenues in the first place. Positions to the right of
M‘ and below
M are feasible in the sense that the levels of outlay on
G required can be financed by levies on the designated tax base,
B. If the relationships are as depicted in Figure 7.2, the king’s surplus is maximized at
E, where the “marginal cost” of producing more
G is equal to the “marginal revenue” generated by that provision (where the slope of
QT is unity). At this point, spending on
G is measured by 0
L (equal to
LC), and total revenue collections are
LE, with a maximum surplus of
EC. The proportion of revenue spent on
G, the
a previously noted, is
LC/
LE. This illustration demonstrates that tax institutions—and specifically the selection of an appropriate tax base—may serve to ensure that the king (or, more generally, the monopoly government) will spend a share of tax revenues on financing valued output. He will do so to maximize his own utility, without any enforcing agency, in a setting where, if there were no such relation between the tax base and
G, spending on
G would be nil.
The surplus-maximizing solution for government or the king may, however, generate varying levels of
G, depending on the tax base selected and on the precise shape of the complementary relationship between the base and the public good. Suppose, for example, that a tax base,
B*, is selected such that
QT shifts to the shape shown by
QT* in Figure 7.2. Net surplus is maximized at
E*. But
G* may not be the predicted efficient level of outlay on the valued public good; such a constitutional arrangement may succeed in raising
a only to ensure that an unduly restricted level of outlay be undertaken by government.
The construction does suggest, however, that, if there should exist an unconstrained choice among possible tax bases, with varying degrees of complementarity between these and the public good, an optimum optimorum solution might be imposed constitutionally. This would require that the tax base be selected such that, when the king levies the allowable revenue-maximizing proportional tax rate on this base, the only viable budgetary position requires that virtually all funds collected be spent on providing the good and, further, that these funds will purchase precisely the efficient quantity, as predicted at the constitutional level. Such a solution is shown at
E‘, where
G‘ is the predicted efficient level of outlay on the public good, and where
Q‘
T‘ suggests that the position at
E‘ is the only possible position for viable budgetary behavior on the part of the government. In the limit, there is no surplus left over for exploitation by the revenue-maximizing, perquisite-seeking king. Under such constitutional “fine tuning” as this, the problem of ensuring the predicted efficient level of outlay is incorporated into the problem of ensuring that revenues collected will be disposed efficiently.
Possible criticism of the analysis at this point involves the unconstrained-choice assumption. Such fine tuning may not be possible, especially when it is recognized that the complementarity relationships for feasible tax-base usage may be severely restricted in number, and, even among the feasible set, the relationships may be narrowly confined. Constrained optimization for the potential taxpayer-beneficiary will in general require trade-offs between allowing the king additional surplus, on the one hand, and accepting levels of public-goods outlay which differ from that desired.
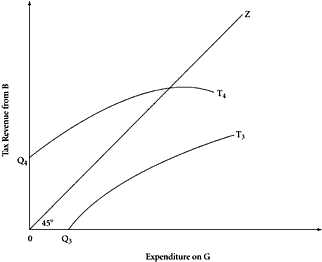 |
| Figure 7.3 |
Indeed, far from there being an unconstrained choice over tax base, each generating a different level of
G and amount of king’s surplus, we must face the possibility that there will be no tax base available that constrains the king to produce any
G at all. To demonstrate some of the effective limits on the central proposition, consider Figure 7.3. If a tax base selected is too narrow in relation to the public good in question, a viable budgetary solution may prove impossible. For example, consider a situation like that depicted by the curve
Q3T3 in Figure 7.3, which lies entirely below the 45° line. As an illustration, suppose that an attempt were made to finance highways exclusively by taxes on automobile air conditioners. It is probable that the revenue-maximizing tax on such a narrow base would generate far less revenue than would be required even to maintain a road network, much less construct it. A second possibility might be that the complementarity between a selected base and the public good might be insufficiently strong to offer any incentive for public-goods provision by the surplus-maximizing king. Consider a situation as depicted in the
Q4T4 curve in Figure 7.3, which, as drawn, has a slope less than unity over its entire range. Unless otherwise constrained, and despite the complementarity between the tax base and the public good, the king will maximize his own surplus by providing none of the good, by keeping
a at zero.
What is required for the disciplinary influence of selected tax-base constraints on governmental fiscal behavior in disposing of tax revenues is a tax base that exhibits a
strongly complementary relationship with the public good
and is sufficiently broad to finance its provision. It is not entirely obvious that such a tax base will be available for each of the public goods that the taxpayer-voter might demand. We can, however, think of some examples where the required relation does hold—and the highway-public road case is one such. In the absence of a road network, few automobiles would be privately purchased and used. In the presence of a road network, automobile usage is “supplied.” Hence, a general constitutional requirement that roads be financed exclusively by taxes levied on automobiles (perhaps along with other privately purchased road-using inputs—gasoline, oil, tires, etc.) will ensure that the government, even in the model of the pure surplus-maximizing king, will spend some part of its tax revenues on road construction and maintenance.
7.3. The Surplus Maximizer: Algebraic Treatment
The basic relationships inherent in our central proposition, along with the limits within which these relationships must operate, may be more fully captured in a simple algebraic model.
In our discussion, the king is taken to maximize
| Y k = R* – G, |
(4) |
where
R* is the maximum revenue that can be derived from the assigned tax base,
B.
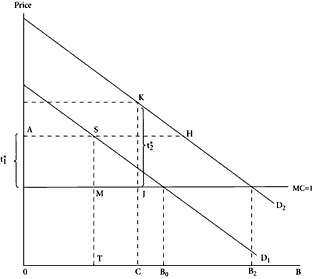 |
| Figure 7.4 |
When the maximum revenue rate
t* is applied to base
B, total expenditure on base
B, gross of tax, is depicted by
B*. For example, in Figure 7.4, when
D1 is the demand curve for
B,
B* is the area
ASTO. We can, on this basis, specify revenue
R* as
| R* = a · B*, |
(5) |
where
a is the proportion of gross of tax expenditure
B* represented by tax revenues.
The parameter
a in (5) can be rewritten as
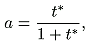 |
(6) |
where
t* is the revenue-maximizing tax rate, expressed as a proportion of net-of-tax expenditure (as in Chapters 3 through 6).
Now, we have specified that the tax base is chosen so as to depend on the level of public outlay on the public good,
G. So
| B* = B*( G), |
(7) |
and
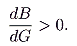 |
(8) |
In general, the revenue-maximizing tax rate,
t*, and hence the parameter,
a, will also depend on the level of public-goods supply. Consequently, we can rewrite (4) as
| Y k = a( G) · B*( G) – G. |
(9) |
We can now examine how
Y
k, the government’s maximand, responds to changes in expenditure on
G. Consider
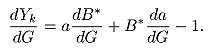 |
(10) |
If the selection of the tax base
B is to exert a constraining effect on the government’s disposition of revenues, then (10) must be greater than or equal to zero over the relevant range.
Complementarity between
B and
G in the relevant range implies that
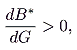 |
(11) |
but this is not sufficient, clearly, to ensure that (10) is positive. Since
a is always less than 1 [see equation (6)], we would seem to require both that
B* be very responsive to changes in
G and that
da/
dG also be positive. In fact, since
B* is potentially large, it does seem possible that the second term in (10) may predominate. Therefore, the sign of
da/
dG may be crucial.
In fact, under plausible assumptions, it seems as if
da/
dG will be positive. To see this, consider Figure 7.4. As the level of
G rises, the demand curve for
B depicted as
D1 in Figure 7.4 moves outward by virtue of the complementarity relation. Suppose that when there is a particular increase in
G, it moves in a parallel fashion to take up the position
D2. The new revenue-maximizing equilibrium will be at 0
C, which is half of 0
B2. The new revenue-maximizing tax rate,
t2*, is the distance
JK. We need to show that
JK exceeds
SM, that is, that the increase in
G has led to an increase in the revenue-maximizing tax rate and hence in the parameter
a. Now,
TC is exactly half of
B0B2 and hence exactly half of
SH. It follows that
K must lie on
D2 above and to the left of
H, so that
KJ must exceed
SM; that is,
t2* >
t1*.
If
t2* >
t1*, then
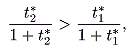 |
and
da/
dG > 0. We can examine nonparallel shifts in
D1 in response to increases in
G supply, but in all cases in which
D2 lies entirely above
D1, given our linearity assumptions, the revenue-maximizing tax rate will increase. Only in the special and somewhat implausible case in which
D1 and
D2 are coincident on the vertical axis will
t* not increase: in this special case,
t* and hence
a remain invariant with respect to
G (i.e.,
da/
dG = 0). If this is accepted, then both the first and second terms in (10) will be nonnegative when
B and
G are complementary: there is therefore some presumption that increases in
G may lead to increases in
Y
k, and hence be desired by Leviathan.
Let us suppose, however, that condition (10) is not satisfied. Is there a simple way of increasing the likelihood that it may be met? It would be possible to relate government’s (or the king’s) receipt of revenue from
general sources, unrelated to
B, to the amount of revenue raised from the single source, tax base
B, that is known to be tied to the provision of
G. In such a case,
R* could be set as any multiple,
b, of its value defined in (5). Hence, in lieu of (5), we have
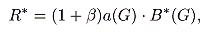 |
(12) |
where
b > 0 and
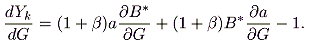 |
(13) |
Clearly, if both
dB*/
dG and
da/
dG exceed zero, (13) exceeds (10) for
b > 0, for a given value of
G in the relevant range; and there exists some value for
b which will guarantee that (13) is positive for positive values for
G. Moreover, the higher the value of
b, the larger the value of
G for which (13) is zero.
*93 Therefore, by increasing the value of
b, we can both ensure that the king will want to provide some
G, and increase the amount of
G thereby obtained (at least up to the point where the complementarity relationship ceases).
While accepting this emendation analytically, it may be challenged on the grounds that it seems inconsistent with the underlying institutional assumptions. While one can imagine the possibility that the king’s ability to raise general revenue might be tied to the revenue from base
B, it does seem as if, once he has been allowed access to some more general tax source, he would use that source exclusively and spend all the revenue on private goods. In a more realistic institutional setting, however, it may be possible to establish a bureau whose sole function is to raise revenue from some general source, under the constraint that it be handed over directly to other public-goods-supplying bureaus in direct relation to the latters’ revenue-raising activities from the assigned complementarity tax bases.
*94
If even this seems implausible, roughly the same effect might in any case be achieved by assigning several tax bases to government, all of which are complements to the public good,
G. Suppose that there should exist a whole set of potential bases,
B1,
B2, … ,
B
n. Consider assigning both
B1 and
B2 for usage as possible tax bases to the surplus-maximizing king. In this case,
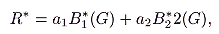 |
(14) |
and
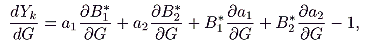 |
(15) |
where
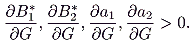 |
(16) |
As before, (15) exceeds (10) for values of
G in the relevant range, and the value of
G for which (15) is zero (if it exists) exceeds the comparable value of
G in (10). Hence, by adding bases to the government’s taxing retinue, all of which are complements to
G, we both increase the possibility that it will prove profitable to provide some public goods, some
G, and increase the level of
G that will be provided.
*95
7.4. The Nonsurplus Maximizer
Before turning to possible policy implications, it will be useful to modify the analysis in the direction of a more widely shared image of government. What effect will be exerted on rational constitutional choices among tax instruments if the model is changed so as to allow the institutions that supply public goods—be these kings, bureaucrats, politicians, or judges—to be somewhat less intractable than the earlier treatment makes them appear? The most selfish of kings or bureaucrats may supply some public goods, even from purely self-interested motivations, especially if they themselves secure shares in the nonexcludable benefits. Some law and order, some defense, some fireworks, will be supplied by a king for his own benefit; and the masses can then be expected to secure spillover benefits. Beyond this, political decision makers, even if unconstrained directly by the citizenry, may be honorable men and women motivated by a genuine sense of public duty; kings may care about their subjects.
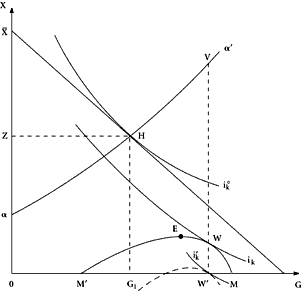 |
| Figure 7.5 |
We now want to allow for this, while retaining the assumption that the government will attempt to maximize revenues from any tax base or bases assigned to it. We want to examine a model in which some
G will be provided due to the king’s utility function. In Figure 7.5, assume that some arbitrarily chosen tax base yields a maximum revenue to the king of 0
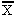 . If the king is a pure surplus maximizer as previously analyzed, he will, of course, retain all of this revenue for personal usage. If, however,
. If the king is a pure surplus maximizer as previously analyzed, he will, of course, retain all of this revenue for personal usage. If, however,
G is included as an argument in his utility function, he will want to provide some
G. The king’s preferences in this case may be represented in a set of indifference contours defined on
B and
G and exhibiting the standard properties. The rate at which a dollar’s worth of revenues in the “king’s” hands can be transformed into a dollar’s worth of outlay on public goods is, of course, unity. Hence, the “price line” faced by the king is the 45° line drawn southeasterly from
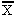 . Equilibrium is attained at
. Equilibrium is attained at
H; the amount of revenue “given up” to provide the public good is
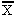 Z; the amount of revenue retained as surplus is 0
Z; the amount of revenue retained as surplus is 0
Z, with the ratio
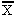 Z/0
Z/0
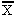 being the
being the
a previously discussed, although in this case its value is determined behaviorally rather than exogenously set, as previously assumed. This ratio is simply the king’s average propensity to consume
G out of revenues collected.
The curve
aa‘ in Figure 7.5 is the locus of equilibrium positions as the “king” is assigned more comprehensive bases for tax levies, all of which are independent of spending on
G. (Note that an
a of unity would imply that this curve lie along the abscissa.)
In the setting depicted in Figure 7.5, what is the effect of substituting a tax base that is complementary to
G for the independent tax bases assumed in tracing out the
aa‘ curve? To answer this question, we may transform Figure 7.2 into Figure 7.5 by relating surplus to levels of
G. Recall from Figure 7.2 that, at
M‘, there is no net surplus, and that this rises to a maximum at
E, while falling back to zero at
M. We simply translate these results into Figure 7.5 with the same labeling. The curve
M‘
EM now represents the transformation possibilities facing the king. He will attain equilibrium at
W, with
W‘ being the total outlay on
G made. Note that this solution involves more public goods and less surplus than the equilibrium at
E reached in the surplus-maximizing model.
The dramatic difference between this complementary tax-base constraint and its absence can now be indicated by comparing the costs (in terms of surplus retained by the king) of securing the amount of
G shown at
W‘. In the constrained model, these costs are measured by the vertical distance
W‘
W. But, for the same
G, these costs rise to
W‘
V in the unconstrained case. If the potential taxpayer-beneficiary is assumed to be confronted with an unlimited set of choice alternatives, he will conceptually be able to reduce the retained (wasted) surplus to zero in the limiting case, while ensuring that a predicted efficient level of outlay on public goods will be made. In Figure 7.5, if we assume that
W‘ is the efficient level desired, a tax base may be selected that exhibits the complementarity properties required to generate a curve like the dashed one drawn through
W‘. Note that, in contrast to the comparable curve in the surplus-maximizing model, this curve can lie above zero along a part of its range. Surplus is reduced to zero (assuming the required properties of the king’s utility function) because the king places an independent marginal valuation on
G.
7.5. Toward a Tax Policy
The analysis of this chapter indirectly supplies an efficiency argument for a particular form of behaviorally induced earmarking. There need be no constraint that explicitly directs government to use tax revenues for specific spending functions. Instead, the nature of the tax bases, in themselves, ensures that government will be induced to utilize revenues for the spending desired. The normative implication is that each activity of government, each budgetary component, should have assigned to it a specified tax instrument, or set of instruments, designed not merely to ensure a level of revenue adequate to and appropriate for a predicted desirable level of the activity, but more particularly to introduce complementarity between the tax base and the governmental activity. We have already referred to the most obvious real-world example: the financing of roads from gasoline and/or automobile taxes. Government broadcasting financed by taxes on receivers offers another. When possible, the argument suggests that fees and tolls should be used in the governmental sale of partitionable services, perhaps even at the cost of some underutilization of facilities; it is unlikely that there could be tax bases for a good more complementary than the good itself.
Less conspicuous examples are worth mentioning. Earl Thompson has argued for taxes on capital to finance defense on the grounds that capital accumulation leads to the threat of external aggression.
*96 A similar argument might be made as concerns internal law and order. Thompson’s argument is that there will be excessive accumulation of coveted capital in the absence of capital taxation. One implication is that capital and defense outlay are complementary. Leaving aside the major objections to capital taxes discussed in Chapter 5, our analysis could point toward a similar conclusion to Thompson’s, but for somewhat different reasons. A tax on new capital formation might be justified on the grounds that it would encourage outlay on defense against external aggressors and on internal provision of law and order.
*97
The analysis can also be employed normatively to identify perverse elements in observed fiscal arrangements, elements that tend to create incentive structures that oppose those which efficiency in revenue disposition would require. Once again, we can find a good example in transportation. Since 1974, a portion of the U.S. federal tax on gasoline (and indirectly on highway usage) has been allocated to the financing of urban mass transit systems (bus, rail, subway lines). In this case, the base of tax (highway usage) is a
substitute rather than a complement for the public good (transit facility) that the government is supposed to provide. It is clearly in the direct interest of the urban-transit bureaucrats to reduce rather than to increase the supply of public good (to reduce the value of
a) because in so doing they will be able to increase the amount of revenue available for disposition.
Our purpose in the discussion above was to suggest examples for possible application of our analysis. We have made no attempt to determine whether or not the norms suggested for tax policy can be extended to cover all components in the budgets of modern governments. And we have not examined the severe informational requirements necessary for rational choice in a genuine constitutional setting. However, the general institution of earmarked taxes is familiar. The conventional wisdom in normative public-finance theory has condemned earmarking essentially on the grounds that any restriction on revenue usage tends to reduce the flexibility of the budgetary decision maker who is charged with the responsibility of allocating total governmental outlay among activities. This normative argument against earmarked bases is conceived in a benevolent despot image of governmental process, one that envisages a centralized decision maker divorced from the citizenry but always motivated to act strictly in the interests of the latter, in the “public interest.” Such an image is not consistent either with models of democratic decision making or with models that allow some role for the self-interest of politicians and bureaucrats. Once the government is perceived in an institutional setting that bears any remote resemblance to reality, the role of earmarking as one means of securing more efficient fiscal outcomes must be reexamined.
An argument in support of earmarked taxes has been advanced in post-Wicksellian, public-choice theory,
*98 and it will be useful to compare this with that argument which emerges here. If decisions on public spending are assumed to be made democratically even at the postconstitutional level, there is a self-evident argument for requiring that benefits be tied directly to costs. Voters, or their representatives, are likely to choose outcomes more rationally, more efficiently, if they can compare costs and benefits for each separate activity rather than for a multicomponent budget. General-fund financing ensures that fiscal choices are made under almost maximal uncertainty.
Our analysis differs from the standard public-choice model in its basic assumption about postconstitutional political process. We explicitly drop the central assumption that budgetary spending and taxes are determined through an effectively democratic voting process in postconstitutional periods. The argument for the behaviorally induced earmarking that emerges is derived directly from the political model in which in-period fiscal decisions are made by revenue-maximizing politicians-bureaucrats who may have at least some power to secure a share of tax revenues as surplus for themselves. A constitutional utilization of the relations between tax bases and the provision of desired public goods becomes a means of exerting discipline on those who do make fiscal decisions. As such, it is not at all out of place in a democratic decision model, and it may be interpreted as reinforcing other arguments noted above. One plausible model of democracy involves attempts by rotating majority coalitions to maximize net fiscal transfers to their members at the expense of members of minorities. The disciplinary argument for earmarking applies equally well to this model as to the more cynical model of bureaucratic domination. All that is required is that the words “majority coalition” be substituted for the word “king” in the earlier parts of the chapter.
Our basic argument is indeed simple. Effectively designed earmarking may limit the extent to which government, any government, can exploit the taxpaying public; government may be given a positive incentive to provide the goods and services that taxpayers want. The decision makers, whoever these may be, can be kept “honest.”
Journal of Public Economics, 9 (June 1978), 301-18.
level and the
disposition, is the
composition of budgetary outlay as among separate components. We do not discuss this element explicitly, although our analysis does have implications that are relevant.
Pepys’s Diaries, a.d. 1666, Sept. 23 and Oct. 10.” Footnote in “Edinburgh Review and the ‘Greatest Happiness Principle,’ ”
Westminster Review, 22 (October 1829). Reprinted in
Utilitarian Logic and Politics, ed. Jack Lively and John Rees (Oxford: Clarendon Press, 1978), p. 184. The author of the
Westminster Review essay is presumably not known.
G. See William Niskanen,
Bureaucracy and Representative Government (Chicago: Aldine-Atherton, 1971). The model has been subjected to criticism precisely because it fails to allow for any diversion of revenues away from the financing of genuine public goods. See Jean Luc Migué and Gérard Bélanger, “Toward a General Theory of Managerial Discretion,”
Public Choice, 17 (Spring 1974), 27-42.
CC‘ and
NN‘ in Figure 7.1 (i.e.,
d2B*/
dG2 < 0).
Review of Economic Studies, 41 (April 1974), 119-28.
Journal of Political Economy, 82 (July-August 1974), 755-82.
Journal of Political Economy, 71 (October 1963), 457-69. Also see James M. Buchanan,
Public Finance in Democratic Process (Chapel Hill: University of North Carolina Press, 1967), especially chap. 6.

