The Economics of Welfare
By Arthur C. Pigou
WHEN a man sets out upon any course of inquiry, the object of his search may be either light or fruit—either knowledge for its own sake or knowledge for the sake of good things to which it leads. In various fields of study these two ideals play parts of varying importance. In the appeal made to our interest by nearly all the great modern sciences some stress is laid both upon the light-bearing and upon the fruit-bearing quality, but the proportions of the blend are different in different sciences. At one end of the scale stands the most general science of all, metaphysics, the science of reality. Of the student of that science it is, indeed, true that “he yet may bring some worthy thing for waiting souls to see”; but it must be light alone, it can hardly be fruit that he brings. Most nearly akin to the metaphysician is the student of the ultimate problems of physics. The corpuscular theory of matter is, hitherto, a bearer of light alone. Here, however, the other aspect is present in promise; for speculations about the structure of the atom may lead one day to the discovery of practical means for dissociating matter and for rendering available to human use the overwhelming resources of intra-atomic energy. In the science of biology the fruit-bearing aspect is more prominent. Recent studies upon heredity have, indeed, the highest theoretical interest; but no one can reflect upon that without at the same time reflecting upon the striking practical results to which they have already led in the culture of wheat, and upon the far-reaching, if hesitating, promise that they are beginning to offer for the better culture of mankind. In the sciences whose subject-matter is man as an individual there is the same variation of blending as in the natural sciences proper. In psychology the theoretic interest is dominant—particularly on that side of it which gives data to metaphysics; but psychology is also valued in some measure as a basis for the practical art of education. In human physiology, on the other hand, the theoretic interest, though present, is subordinate, and the science has long been valued mainly as a basis for the art of medicine. Last of all we come to those sciences that deal, not with individual men, but with groups of men; that body of infant sciences which some writers call sociology. Light on the laws that lie behind development in history, even light upon particular facts, has, in the opinion of many, high value for its own sake. But there will, I think, be general agreement that in the sciences of human society, be their appeal as bearers of light never so high, it is the promise of fruit and not of light that chiefly merits our regard. There is a celebrated, if somewhat too strenuous, passage in Macaulay’s Essay on History: “No past event has any intrinsic importance. The knowledge of it is valuable, only as it leads us to form just calculations with regard to the future. A history which does not serve this purpose, though it may be filled with battles, treaties and commotions, is as useless as the series of turnpike tickets collected by Sir Matthew Mite.” That paradox is partly true. If it were not for the hope that a scientific study of men’s social actions may lead, not necessarily directly or immediately, but at some time and in some way, to practical results in social improvement, not a few students of these actions would regard the time devoted to their study as time misspent. That is true of all social sciences, but especially true of economics. For economics “is a study of mankind in the ordinary business of life”; and it is not in the ordinary business of life that mankind is most interesting or inspiring. One who desired knowledge of man apart from the fruits of knowledge would seek it in the history of religious enthusiasm, of martyrdom, or of love; he would not seek it in the market-place. When we elect to watch the play of human motives that are ordinary—that are sometimes mean and dismal and ignoble—our impulse is not the philosopher’s impulse, knowledge for the sake of knowledge, but rather the physiologist’s, knowledge for the healing that knowledge may help to bring. Wonder, Carlyle declared, is the beginning of philosophy. It is not wonder, but rather the social enthusiasm which revolts from the sordidness of mean streets and the joylessness of withered lives, that is the beginning of economic science. Here, if in no other field, Comte’s great phrase holds good: “It is for the heart to suggest our problems; it is for the intellect to solve them…. The only position for which the intellect is primarily adapted is to be the servant of the social sympathies.”… [From the text]
First Pub. Date
1920
Publisher
London: Macmillan and Co.
Pub. Date
1932
Comments
4th edition.
Copyright
The text of this edition is copyright © 1932. This book is available through Transaction Publishers, Inc. Direct all requests for permissions and copyrights to Transaction Publishers, Inc.
- Preface to the Third Edition
- Note to the Fourth Edition
- Part I, Chapter 1
- Part I, Chapter 2
- Part I, Chapter 3
- Part I, Chapter 4
- Part I, Chapter 5
- Part I, Chapter 6
- Part I, Chapter 7
- Part I, Chapter 8
- Part I, Chapter 9
- Part I, Chapter 10
- Part I, Chapter 11
- Part II, Chapter 1
- Part II, Chapter 2
- Part II, Chapter 3
- Part II, Chapter 4
- Part II, Chapter 5
- Part II, Chapter 6
- Part II, Chapter 7
- Part II, Chapter 8
- Part II, Chapter 9
- Part II, Chapter 10
- Part II, Chapter 11
- Part II, Chapter 12
- Part II, Chapter 13
- Part II, Chapter 14
- Part II, Chapter 15
- Part II, Chapter 16
- Part II, Chapter 17
- Part II, Chapter 18
- Part II, Chapter 19
- Part II, Chapter 20
- Part II, Chapter 21
- Part II, Chapter 22
- Part III, Chapter 1
- Part III, Chapter 2
- Part III, Chapter 3
- Part III, Chapter 4
- Part III, Chapter 5
- Part III, Chapter 6
- Part III, Chapter 7
- Part III, Chapter 8
- Part III, Chapter 9
- Part III, Chapter 10
- Part III, Chapter 11
- Part III, Chapter 12
- Part III, Chapter 13
- Part III, Chapter 14
- Part III, Chapter 15
- Part III, Chapter 16
- Part III, Chapter 17
- Part III, Chapter 18
- Part III, Chapter 19
- Part III, Chapter 20
- Part IV, Chapter 1
- Part IV, Chapter 2
- Part IV, Chapter 3
- Part IV, Chapter 4
- Part IV, Chapter 5
- Part IV, Chapter 6
- Part IV, Chapter 7
- Part IV, Chapter 8
- Part IV, Chapter 9
- Part IV, Chapter 10
- Part IV, Chapter 11
- Part IV, Chapter 12
- Part IV, Chapter 13
- Appendix I
- Appendix II
- Appendix III
Part I, Chapter VI
THE MEASUREMENT OF CHANGES IN THE SIZE OF THE NATIONAL DIVIDEND
§ 1. THE discussion of the preceding chapter has provided us with a
criterion by which to decide whether the national dividend of one period is larger or smaller than the national dividend of another period from the point of view of one or other of the periods. But to provide a
criterion of increases and decreases in the size of anything is not to provide a
measure of these changes. We have now to study the problem of devising an appropriate measure.
§ 2. Our
criterion of increase from the point of view of any period being that, with the tastes and distribution of that period, the money demand for the things that have been added to the dividend exceeds the money demand for the things taken away from it, it is natural to suggest that we should employ as a
measure of increase, from the point of view of the period, the proportion in which the aggregate money demand for the things contained in the dividend of that period (in the sense of the amount of money that people would be willing to give rather than do without those things) exceeds the aggregate money demand for the things contained in the dividend of the other period. A measure of this kind would conform exactly to our criterion. We should have two figures, one giving the change from the point of view of the tastes and distribution of period I. and the other that from the point of view of the tastes and distribution of period II. Plainly, given the criterion decided upon in the last chapter, this is the measure that we should adopt if we were able to do so.
§ 3. Unfortunately, however, this type of measure is
altogether impracticable. In the way of it there stands, as a final obstacle, the fact that the aggregate money demand for the things contained in the dividend of any period, in the sense explained above, is an unworkable conception. It involves the money figure that would be obtained by adding together the consumers’ surpluses, as measured in money, derived from each several sort of commodity contained in the dividend. As Marshall has shown, however, the task of adding together consumers’ surpluses in this way, partly on account of the presence of complementary and rival commodities, presents difficulties which, even if they are capable of being overcome in theory by means of elaborate mathematical formulae, are certainly insuperable in practice.
*58 Even apart from these remoter complications, it is evident that no measure of the kind contemplated could be built up which did not embrace among its terms the elasticities of demand for the various elements contained in the dividend, or, more exactly, the forms of the various demand functions that are involved. These data are not, and are not likely, within any reasonable period of time, to become, accessible to us. Any type of measure which involves the use of them must, therefore, be ruled out of court.
§ 4. Continuing along the line of thought which this consideration suggests, we are soon led to the conclusion that the only data which there is any serious hope of organising on a scale adequate to yield a measure of dividend changes are the quantities and prices of various sorts of commodities. There is nothing else available, and, therefore, if we are to construct any measure at all, we
must use these data. Our problem then becomes: in what way, if at all, is it possible, out of them, to construct a measure that will conform to the definition of changes in the size of the dividend that was reached in the last chapter? An attempt to solve this problem falls naturally into three parts: first, a general inquiry as to what measure would conform most nearly to that definition if all relevant information about quantities and prices were accessible; secondly, a mathematical inquiry as to what practicable measure built up from the sample information
about quantities and prices that we can in fact obtain would approximate most closely to the above measure; thirdly, a mixed general and mathematical inquiry as to
how reliable the practicable measure, as an index of the above measure, is likely to be.
§ 5. In attacking the first and most fundamental of these issues we have to admit at once that complete success is unattainable. According to the definition of the last chapter, the national dividend will change in one way from the point of view of a period in which tastes and distribution are of one sort, and in a different way from that of a period in which they are of another sort. In order to conform with this, our measure of change would need to be double, being expressed in one figure from the point of view of the first period, and, if tastes and distribution were different in the two periods, in another figure from the point of view of the second period. A measure built up on quantities and prices only cannot possibly answer to this requirement. For, though we may know the quantities and prices that actually ruled in period I., when tastes and distribution were of sort A, and the quantities and prices that ruled in period II., when tastes and distribution were of sort B, we cannot possibly know either the quantities and prices which would have ruled in period I., if tastes and distribution had then been of sort B, or those which would have ruled in period II., if tastes and distribution had then been of sort A. Hence, the utmost we can hope for is a measure which will be independent of what the state of tastes and distribution actually is in either of the periods to be compared, but which will always increase when the content of the dividend has changed in such a way that economic welfare (as measured in money) would be increased whatever the state of tastes and distribution, provided only that this was the same in both periods. Even if the whole of the data about quantities and prices were accessible to us, it would be impossible to construct a measure, based on these data alone, conforming more closely than this to our definition; and, plainly, this degree of conformity is very incomplete.
§ 6. So much being understood, let us turn to the problem
of constructing from full data a measure—we may call it from henceforth the full-data measure—that will conform as closely as possible to the modest ideal specified in the preceding section. What is required is a measure which will show increases in the size of the dividend whenever its content is changed in such a way that, in terms of the money of either period,
*59 for a group of given size with constant tastes and distribution, the money demand for the items that have been added is greater than the money demand for those that have been subtracted;
*60 or, in other words, that the economic satisfaction (as measured in money) obtained by the group in the second period is greater than it was in the first period. It is not, of course, required that, if, when the excess of economic satisfaction (as measured in money) is E, our measure shows an increase of 1 per cent, it shall, when the excess of economic satisfaction (as measured in money) is 2E, show an increase of 2 per cent. This is not only not necessary, but, in the special case of a dividend consisting of one sort of commodity only, it would even lead to paradoxical results. It is required, however, that, when the excess of economic satisfaction (as measured in money) is E, our measure shall show
some increase, and that, when the excess of economic satisfaction (as measured in money) is more than E, it shall show a greater increase than it does when the excess is E. This is the framework within which our construction must be made. The problem is to discover what construction will best fulfil the purpose that has been specified.
*61
§ 7. In the first of any two periods that we wish to compare any group of given size expends its purchasing power upon one collection of commodities, and in the second on a different collection. Each collection must, of course, be so estimated that the same thing is not counted twice over, that is to say, it must be taken to include direct services rendered to consumers—
e.g. the services of doctors, finished consumable articles, and a portion of the finished durable machines produced during the year,
*62 but not the raw materials or the services of labour that are embodied in these things, and not, of course, “securities.” Let us, at this stage, ignore the fact that in one of the collections there may be some newly invented kinds of commodity which are not represented at all in the other. The first collection, which we may call C
1, then embraces
x
1, y
1, z
1,…units of various commodities; and the second collection, C
2, embraces
x
2, y
2, z
2,…units of the same commodities. Let the prices per unit of these several commodities be, in the first period,
a
1, b
1, c
1,…;
and, in the second period,
a
2, b
2, c
2,…Let the aggregate money income of our group, in the first period, be I
1, in the second I
2. The following propositions result:
1. If our group in the second period purchased the several commodities in the same proportion in which it purchased them in the first period, that is to say, if it purchased in both periods a collection of the general form C
1, its purchase of each commodity in the second period would be equal to its purchase of each commodity in the first period multiplied by the fraction
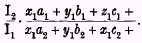
2. If our group in the first period purchased the several commodities in the same proportion in which it purchased them in the second period, that is to say, if it purchased in both periods a collection of the general form C
2, its purchase of each commodity in the second period would be equal to its purchase of each commodity in the first period multiplied by the fraction
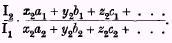
On the basis of these propositions, provided that a certain assumption is made, our problem can be partially solved.
§ 8. If in period II. a single man who had been purchasing a collection of the form C
2,
i.e. made up of elements in the proportions (
x
2, y
2, z
2,…), chose instead to purchase a collection of the form C
1, it is certain that his action would leave prices unchanged, so that he could buy the items in his new collection at prices
a
2, b
2, c
2,… An analogous proposition holds of a single man in period I. who should choose to shift from a collection of form C
1 to one of form C
2. But, when it is the whole of a group, or, if we prefer it, a representative man, who shifts his consumption in this way, it is no longer certain that prices would be unaffected. If the group in period II. shifted from a collection of form C
2 to one of form C
1, it would have to pay, let us suppose, prices
a
1‘, b
1‘, c
1‘ In like manner, if the group in period I. shifted from a collection of form C
1 to one of form C
2, it would have to pay prices
a
2‘, b
2‘, c
2‘ The assumption referred to at the end of
the preceding section is that {
x
1a
1‘ + y
1b
1‘ + z
1c
1‘ +…} is equal to {
x
1a
1 + y
1b
1 + z
1c
1 +…} and that {
x
2a
2‘ + y
2b
2‘ + z
2c
2‘ +…} is equal to {
x
2a
2 + y
2b
2 + z
2c
2 +…}. This means that the group in period II. could then, if it chose, buy as much of a C
1 collection, in spite of the shift of prices caused by its decision to do this, as it would have been able to do had that decision caused no shift of prices; and that an analogous proposition holds of the group in period I. If all the commodities concerned were being produced under conditions of constant supply price, the above assumption would conform exactly to the facts. In real life, with a large number of commodities, it is reasonable to suppose that the upward price movements caused by shifts of consumption would roughly balance the downward movements; so that, in general, our assumption will conform approximately to the facts. It is important to remember, however, throughout the following argument, that this assumption is being made.
§ 9. Let us begin with the case in which both the fractions set out in § 7 lie upon the same side of unity; they are either both greater than unity or both less than unity. If they are both greater than unity, this means that our group, if it wishes, can buy more commodities in the second period than in the first, whether its purchases are arranged in the form of collection C
1 or in that of collection C
2. Hence the fact that in the second period it chooses the form C
2 proves that the economic satisfaction (as measured in money) yielded by what it then purchases in the form C
2 is greater than the economic satisfaction (as measured in money) that would be yielded by a collection of the form C
1 larger than the collection of that form which it purchased in the first period.
*63A fortiori, therefore, it is greater than the economic satisfaction (as measured in money) that would be yielded by the actual collection of the form C
1 which it purchased in the first period.
But, since tastes and distribution are unaltered, the economic satisfaction (as measured in money) that would be yielded by the actual collection C
1 in the second period is equal to the economic satisfaction (as measured in money) that was yielded by the actual collection in the first period. Hence, if both our fractions are greater than unity, it necessarily follows that the economic satisfaction (as measured in money) yielded by the collection C
2 bought in the second period is greater than the economic satisfaction (as measured in money) yielded by the collection C
1 bought in the first period. By analogous reasoning it can be shown that, if both the above fractions are less than unity, the converse result holds good. In these circumstances, therefore, either of the two fractions
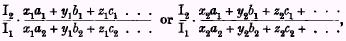
or any expression intermediate between them, will satisfy the condition, set out in § 6, which our measure is required to fulfil as a criterion of changes in the volume of the dividend.
§ 10. In the above circumstances, therefore, the condition we have laid down does not determine the choice of a measure, but merely fixes the limits within which that choice must lie. The width of these limits depends upon the extent to which the two fractions differ from one another. In some conditions there exists between them a relation of approximate equality. Thus, during the later nineteenth century, the dominant factor in the Englishman’s increased capacity to obtain almost every important commodity was one and the same, namely, improved transport; for a main part of what improvements in manufacture accomplished was to cheapen means of transport. In other conditions the difference between the two fractions is considerable. Illustrations that would be directly applicable might perhaps be found. I must content myself, however, with one drawn, not from an inter-temporary comparison of two states of the same group, but from a contemporary comparison of the states of two groups. This illustration is only relevant to the present purpose on the unreal assumption that English and German workmen’s tastes are the same and that their purchases differ solely on account of differences in
their income and in the prices charged to them. It is taken from the Board of Trade’s Report on the
Cost of Living in German Towns. The Report shows that, at the time when it was made, what an English workman customarily consumed cost about one-fifth more in Germany than in England, while what a German workman customarily consumed cost about one-tenth more in Germany than in England.
*64 If, then, the letters with the suffix 1 be referred to English consumption and prices, and those with the suffix 2 to German consumption and prices,
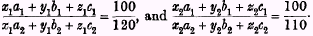
§ 11. Though our condition, in the class of problem so far considered, only fixes these two limits within which the measure of dividend changes should lie, considerations of convenience suggest even here the wisdom of selecting, though it be in an arbitrary manner, some one among the indefinite number of possible measures. When we proceed from this class of problem to another more difficult class, the need for purely arbitrary choice is narrower in range. It sometimes happens that one of the above two fractions is greater than unity and the other less than unity. Then it is clear that both of them cannot indicate the direction in which the economic satisfaction (as measured in money) enjoyed by the group has changed. In the second period, let us suppose, the group’s later income commands a larger amount of the collection of form C
2 than its earlier income commanded; but it commands a smaller amount of the collection of form C
1 than its earlier income commanded. In these circumstances common sense suggests that, if the fraction
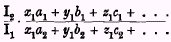
falls short of unity by a large proportion, while the fraction
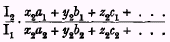
exceeds unity only by a small proportion, the economic
satisfaction (as measured in money) enjoyed by our group has
probably diminished; and that, if conditions of an opposite character are realised, it has probably increased. A like inference, it would seem, may be drawn, though with less confidence, when one fraction differs from unity in only a
slightly greater proportion than the other. If this be so, the economic satisfaction—it will be understood that we are speaking of satisfaction as measured in money—obtained by our group
probably decreases or increases in the second period according as either
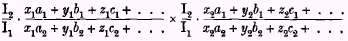
or any power of this expression, or any other formula which moves more or less as it does, is greater or less than unity. Any fraction constructed on these lines will, therefore,
probably satisfy the conditions required of our measure.
§ 12. In former editions of this work the above commonsense view was defended by direct analysis as follows. If
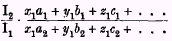
is less than unity by a large fraction, this means that, were our group to purchase in the second year a collection of the form C
1, its purchases of each item would be less by a large percentage than they were in the first year, and therefore—tastes and distribution being unchanged—it would probably enjoy an amount of satisfaction less than in the first year by a large amount, say by K
1. The fact that, instead of doing this, it purchases in the second year a collection of the form C
2 proves that the satisfaction yielded by its purchase of this collection in the second year does not fall short of that yielded by its purchase of the other collection in the first year by more than K
1. In like manner, if
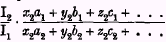
is greater than unity by only a small fraction, this means that, were our group to purchase a collection of the form C
2 in the first year, its purchases of each item would be less by only a small percentage than they are in the second year, and—tastes and distribution being unchanged—it would
probably enjoy an amount of satisfaction less than in the second year by only a small amount, say K
2. Hence, the satisfaction yielded by the collection actually purchased in the second year does not exceed that yielded by the collection actually purchased in the first year by more than K
2. Since, therefore, in view of the largeness of K
1 relatively to K
2, there are more ways in which the satisfaction from the second year’s purchase can be less, than there are ways in which it can be more, than the satisfaction from the first year’s purchase, and since, further, the probability of any one of these different ways is
prima facie equal to that of any other, it is
probable that the satisfaction from the second year’s purchase is less than that from the first year’s. This line of reasoning now seems to me to depend on a
priori probabilities in a manner that is not correct. It is necessary to look at the matter more closely. To this end let us write
q1 for the quantity of collection C
1 obtainable (and obtained) with the then income in period I.:
q2 for the quantity of collection C
1 obtainable with the then income in period II.:
r1 for the quantity of collection C
2 obtainable with the then income in period I.:
r2 for the quantity of collection C
2 obtainable (and obtained) with the then income in period II.: and φ(
q1), φ(
q2), F(
r1) and F(
r2) for the quantities of satisfaction (as measured in money) associated with these several actual and potential purchases.
We are given that
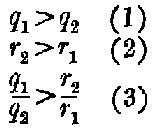
Then, since
q1 of C
1 is preferred in period I. to
r1 of C
2, we know that φ(
q1)>F(
r1). In like manner we know that F(
r2)>φ(
q2). Further, from (1) φ(
q1)>φ(
q2; and from (2) F(
r2)>F(
r1).
Write
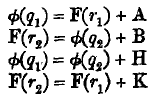
Thus A, B, H and K are all positive, and, by simple transposition, φ(
q1) – F(
r2) = ½(A-B+H-K). The inequality (3), at all events if the excess of
q1/
q2 over
r2/
r1 is considerable, permits us to say that
probably H>K. But we know nothing about the values of A and B. The so-called principle of non-sufficient reason does not entitle us to educe out of this nescience the proposition that
probably (B-A)<(H-K). It is only, however, with the help of some such proposition that we can infer that φ(
q1) is
probably > F(
r2). Hence no general proof of our common-sense view is possible. It is true that, the larger the excess of
q1/
q2 above
r2/
r1,
the more likely it is that satisfaction in the second period will be less than satisfaction in the first; but we cannot specify any values for these quantities in respect of which satisfaction in the second period is
more likely than not to be less than satisfaction in the first. As Mr. Keynes puts it, “We are faced with a problem in probability, for which in any particular case we may have relevant data, but which, in the absence of such data, is simply indeterminate.”
*65
§ 13. If this conclusion is correct it follows that, when of the expressions
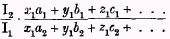
and
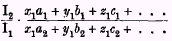
one is greater and the other less than unity, there is
no intermediate expression of which we can say in general terms that the economic satisfaction obtained by our group probably increases or decreases in the second period according as the expression is greater or less than unity. Nevertheless, when both our limiting expressions are on the same side of unity, so that there is no doubt as to whether economic satisfaction, as between the two periods, has increased or diminished, it is practically much more convenient to write down some single expression intermediate between the two limiting expressions rather than both of these. There are an infinite number of intermediate
expressions available. In making our choice among them, since there is no deeper ground of preference, we may, as Mr. Keynes writes, “legitimately be influenced by considerations of algebraical elegance, of arithmetical simplicity, of labour-saving, and of internal consistency between different occasions of using a particular system of short-hand.”
*66 It is thus, I suggest, proper to make use of the two fundamental tests of technical excellence in price index numbers—for, of course, the measure we are seeking is simply the reciprocal of a price index number multiplied by the proportionate change that has taken place in money incomes—which Professor Irving Fisher has brought into prominence. First, the formula chosen should be such that “it will give the same ratio between one point of comparison and the other point, no matter which of the two is taken as base.”
*67 If, calculated forward, it shows that in 1910 prices were double what they were in 1900, it must not, as a so-called unweighted arithmetical index number of the Sauerbeck type would do, show, when calculated backwards, that in 1900 prices were something other than half what they were in 1910. Secondly, the formula chosen should obey what Professor Fisher calls the factor-reversal test. “Whenever there is a price of anything exchanged, there is implied a quantity of it exchanged, or produced, or consumed, or otherwise involved, so that the problem of an index number of
prices implies the twin problem of an index number of quantities…. No reason can be given for employing a given formula for one of the two factors which does not apply to the other.”
*68 Hence, the formula chosen should be such that, assuming the aggregate money values of all the commodities we are studying to have moved between two years from E to (E+
e), then, if the formula, as applied to prices, gives an upward movement from P to (P+
p) and, as applied to quantities, an upward movement from Q to (Q+
q),
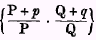
Besides conformity with these tests we may also properly
require in our measure simplicity of structure and convenience of handling. These various considerations taken together point, on the whole, to the formula
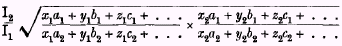
as the measure of change most satisfactory for our purpose. The portion of this expression to the right of
I2/
I1 is the reciprocal of that form of price index number to which Professor Fisher assigns the first prize for general merit, and which he proposes to call “the ideal index number.”
*69
§ 14. The formulae discussed so far, alike the limiting formulae and the intermediate formula, have been built up on the tacit assumption that no commodities are included in either of the collections C
1 and C
2, which are not included in both. If, therefore, a commodity is available for purchase in one of any two years but not in the other, the satisfaction yielded by this commodity in the year in which it is purchased is wholly ignored by these measures. So far then as “new commodities” are introduced between two periods which are being compared, the measures are imperfect. This matter is important, because new commodities, in the sense here relevant, embrace, not merely commodities that are new physically, but also old commodities that have become obtainable at new times or places, such as strawberries in December, or the wheat which railways have introduced into parts of India where it was formerly unknown. Obviously, we must not count December strawberries along with ordinary strawberries, and so make inventions for strawberry forcing raise the price of strawberries, but must reckon December strawberries as a new and distinct commodity. Since, however, new commodities seldom play an important part in the consumption of any group till some little while after they are first introduced, the imperfection due to this is not likely to be very serious for comparisons between two years that are fairly close together. We can
ignore the existence of the new commodities and confine our calculations to the old ones without serious risk of invalidating our results. As between distant years, however, in the later of which a great number of important commodities may be available that did not exist at all in the earlier ones, a measure that ignored new commodities would be almost worthless as a gauge of changes (as defined in the preceding chapter) in the size of the national dividend.
*70 Unless, therefore, some way can be found of bringing these things into account, the hope of making comparisons over other than very short intervals must, it would seem, be abandoned. A way out of this impasse is, however, available in the chain method devised by Marshall.
*71 On this method, the price level of 1900 is compared with that of 1901 on the basis of the commodities available in both those years, new commodities introduced and old commodities dropped out during 1901 being ignored; the price level of 1901 is then compared with that of 1902, the new commodities of 1901 this time being counted, but those of 1902 ignored; and so on. Thus we may suppose prices in 1901 to be 95 per cent of prices of 1900; those of 1902, 87 per cent of those of 1901; those of 1903, 103 per cent of those of 1902. On this basis we construct a chain, the price level of 1900 being put at 100. With the above figures the chain will be:
| 1900 | ·· | 100 |
| 1901 | ·· | 95 |
| 1902 | ·· | 82.6 ( i.e. 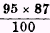 ) ) |
| 1903 | ·· | 85 ( i.e. 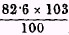 ). ). |
When the reciprocals of these price indices, which obviously
constitute indices of the purchasing power of £1, are put into our measure of the national dividend, we obtain an instrument by which years, too distant from one another to be effectively compared by any direct process, can be compared by a chain of successive stages. It is as though we were unable to construct any measuring rod capable of maintaining its shape if carried more than 100 miles. It would then be impossible to make any direct comparison between the height of the trees in places 1000 miles apart. But, by comparing the trees at the first mile with those at the 100th mile, these with those at the 199th mile, and so on continually, it would be possible to make an indirect comparison.
*72 It must, indeed, be conceded that, if the successive individual comparisons embodied in the chain method, each of which admittedly suffers from a small error, are likely for the most part to suffer from errors
in the same direction, the cumulative error as between distant years may be large. Were people equally likely to forget how to make things now in use as to
invent new things, a large cumulative error would be unlikely. But, in fact, we know that the great march of inventive progress is not offset in this way. Hence the errors introduced by the chain method are likely to be predominantly in one direction, in such wise that, if the method, as between two distant years, gives equal purchasing power for the £, it is
probable that the £ really brings more satisfaction to the representative man of given tastes in the later year that in the earlier. Consequently, if our chain measure in 1900 gave 90 as the index of a £’s purchasing power, and gave 100 as the index in 1920, even though meanwhile a large number of new commodities had been introduced and old commodities abandoned, we might confidently infer that, in the conditions postulated in § 5, the amount of economic satisfaction carried to our group by a £ was larger in 1920 than it had been in 1900. But, if these indices were reversed, we could not infer with equal confidence—indeed, unless the fall of the index were very great, we could not infer with
any confidence—that the sum of economic satisfaction carried by a £ was
smaller in 1920 than in 1900.
§ 15. We now turn to the second main problem of this chapter. The formula of § 13 is the one we should select if our choice was completely free. But it cannot be employed in practice because, in order to construct it, a great deal of information would be necessary which is never in fact available. It is, therefore, necessary to construct, from such information as we can obtain, a model, or representative, measure that shall approximate to it as closely as possible. Our full-data measure, apart from its multiplier
I2/
I1 representing change of income, is built up of two parts: the reciprocal of the price change of the collection C
1 (containing quantities of different commodities equal to
x
1, y
1, z
1,…) and the reciprocal of the price change of the collection C
2 (containing quantities equal to
x
2, y
2, z
2,…). Our approximate measure will, therefore, also be built up of two parts constituting approximations to the price changes of C
1 and of C
2 respectively. By what use of the method of sampling can these approximations best be made?
§16. Whatever be the collection of commodities with which we are concerned, whether it be that purchased at any time by people in general, or by artisans, or by labourers, or by any other body of persons, it is likely to contain commodities drawn from several different groups, the broad characteristics of whose price movements are different. A good sample collection should contain representatives of all the groups with different characteristics that enter into the national dividend, or of that part of it which we are trying to measure.
*73 Unfortunately, however, practical considerations make it impossible that this requirement should be satisfied, and even make it necessary that resort should be had to commodities that do not themselves enter into the purchases of ordinary people, but are, like wheat and barley, raw materials of commodities that do. For the range of things whose prices we are able to observe and bring into our sample collection is limited in two directions.
First, except for certain articles of large popular consumption, the retail prices charged to consumers are difficult to ascertain. Giffen once went so far as to say: “Practically it is found that only the prices of leading commodities capable of being dealt with in large wholesale markets can be made use of.” This statement must now be qualified, in view of the studies of retail prices of food that have been made by the Board of Trade and the late Ministry of Food, but it still holds good over a considerable field. Even, however, when the difficulty of ascertaining retail prices can be overcome, these prices are unsuitable for comparison over a series of years, because the thing priced is apt to contain a different proportion of the services of the retailer and of the transporter, and, therefore, to be a different thing at one time from what it is at another. “When fresh sea fish could be had only at the seaside, its average price
was low. Now that railways enable it to be sold inland, its average retail price includes much higher charges for distribution than it used to do. The simplest plan for dealing with this difficulty is to take, as a rule, the wholesale price of a thing at its place of production, and to allow full weight to the cheapening of the transport of goods, of persons, and of news as separate and most weighty items.”
*74
Secondly, it is very difficult to take account even of the wholesale prices of manufactured articles, because, while still called by the same name, they are continually undergoing changes in character and quality. Stilton cheese, once a double-cream, is now a single-cream cheese. Clarets of different vintages are not equivalent. A third-class seat in a railway carriage is not the same thing now as it was forty years ago. “An average ten-roomed house is, perhaps, twice as large in volume as it used to be; and a great part of its cost goes for water, gas, and other appliances which were not in the older house.”
*75 “During the past twelve years, owing to more scientific methods of thawing and freezing, the quality of the foreign mutton sold in this country has steadily improved; on the other hand, that of foreign beef has gone down, owing to the fact that the supply from North America has practically ceased, and its place has been taken by a poorer quality coming from the Argentine.”
*76 The same class of difficulty is met with in attempts to evaluate many direct services—the services of doctors, for example, which as Pareto pointedly observes, absorb more expenditure than the cotton industry
*77—for these, while retaining their name, often vary their nature.
It would thus seem that the principal things available for observation—though it must be admitted that the official Canadian Index Number and more than one index number employed in United States have attempted a wider survey—are raw materials in the wholesale markets, particularly in the large world markets. These things—apart, of course, from
the war—have probably of late years fallen in price relatively to minor articles, in which the cost of transport generally plays a smaller part; they have certainly fallen relatively to personal services; and they have probably risen relatively to manufactured articles, because the actual processes of manufacture have been improving. The probable tendency to mutual compensation in the movements of items omitted from our samples makes the omission a less serious evil than it would otherwise be. But, of course, the approximation to a true measure is
protanto worsened; and it is almost certain, since the value of raw materials is often only a small proportion of the value of finished products, so that a 50 per cent change in the former might involve only a 5 per cent change in the latter, that it will give an exaggerated impression of the fluctuations that occur.
Nor does what has just been said exhaust the list of our disabilities. For the samples wanted to represent the several “collections” is a list, not merely of prices, but of prices multiplied by quantities purchased: and our information about quantities is even more limited than our information about prices. There are very few records of annual output—still less of annual purchases—of commodities produced at home. Quantities of imports are, indeed, recorded, but there are not very many important things that are wholly obtained by importation. The difficulty can, indeed, be turned, for some purposes, by resort to typical budgets of expenditure. These make it possible to get a rough idea of the average purchases of certain principal articles that are made by particular classes of people. But this method can scarcely as yet provide more than rough averages. It will seldom enable us to distinguish between the quantities of various things which are embodied in the collections representative of different years fairly close together.
§17. Let us next suppose that these difficulties have been so far overcome that a sample embracing both prices and quantities at all relevant periods is available. The next problem is to determine the way in which the prices ought to be “weighted.” At first sight it seems natural that the weights should be proportioned to the quantities of the several commodities that are contained in the collection from which
the sample is drawn, But, in theory at all events, it is sometimes possible to improve upon this arrangement. For some of the commodities about which we have information may be connected with some excluded commodities in such a way that their prices generally vary in the same sense. These commodities, being representative of the others as well as of themselves, may properly be given weights in excess of what they are entitled to in their own right. Thus, ideally, if we had statistics for a few commodities, each drawn from a different broad group of commodities with similar characteristics, it would be proper to “weight” the prices of our several sample commodities in proportion, not to their own importance, but to that of the groups which they represent. This, however, is scarcely practicable. There may be certain commodities whose representative character is so obvious that a doctored weight may rightly be given to them, but we shall seldom have enough knowledge to attempt this kind of discrimination. To use our sample as it stands is, in general, the best plan that is practically available.
*78 Hence, the full-data measure of the price change of the collection C
1 being
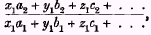
the best available approximation to this will be
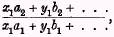
where the number of terms is limited to the number of articles contained in the sample. It follows that the best approximation to the full-data measure of dividend change set out at the end of § 13 is
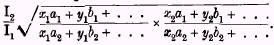
§ 18. In practice, as has already been hinted, we cannot usually find a reasonable sample set of articles, in regard to which the quantities of the same articles purchased in each of the two periods (or places) we are comparing are known. In these circumstances we may have to content ourselves with a sample in which quantities are given only for one of the years in our comparison. In this case we are forced to truncate our formula and adopt the form
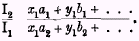
This is the type of formula (inverted) employed by the British Board of Trade in the cost of living index number. Obviously a sample of this truncated sort is inferior to a full sample. But Professor Fisher’s investigations show that it does not usually yield results very widely divergent from those given by the full sample. We need not, therefore, attack the very difficult question whether there may not be some other formula founded on the same data that would give a closer approximation to the full sample.
§ 19. It is, however, desirable at this point to make plain the exact relation between the above formula and that implicit in a so-called “unweighted” index number such as Sauerbeck’s. In that type of index number a certain year or average of years is taken as base, the prices of all commodities for this base year or base-period are put at 100, and the prices for other years at the appropriate fractions of 100. If
a
1, b
1, c
1, are the actual prices in the base-year, and
a
2, b
2, c
2, the actual prices in the other year, the index of a £’s purchasing power for this other year will be
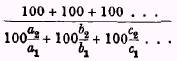
This is equivalent to the formula given in the preceding section if and only if
x
1, y
1, z
1,… in that formula have values proportioned to
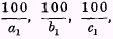 …
…That is to say, the Sauerbeck formula measures the changes that take place in the aggregate price of a collection made up of such quantities of each sort of commodity as would, in the base-year or base-period, have sold for equal multiples of £100. It is extremely improbable that, as a matter of fact, those quantities were the quantities actually sold in the base-year or base-period. Therefore, it is only by an extraordinary accident that a formula constructed on the Sauerbeck plan with any given year or period as base will coincide with a formula modelled on the plan of the preceding section and designed to display the changes that occur in the aggregate price of the collection that was actually sold in the base-year or base-period.
§20. To what has just been said an obvious corollary attaches. We have seen that an index number on the Sauerbeck plan is built up with any year or period R as base; it measures changes in the aggregate price of a collection made up of such quantities of each commodity as in the year R would have sold for £100. It follows that, when the base is shifted from the year R
1 to the year R
2, the collection whose aggregate price movements are being measured is, in general, altered. Since, then, a different thing is being measured, it is to be expected that a different result will be attained; and there is no reason why the results should not differ so far that an index number on base R
1 shows a rise in the purchasing power of money, while a similar number (of the Sauerbeck type) on the base R
2 shows a fall. Thus, if we have to do with two commodities only, one of which doubles in price while the other halves, this type of index number will show a 25 per cent rise in the price of the two together if the first year is taken as base and a 20 per cent fall if the second year is taken. An excellent practical illustration of this type of discrepancy is afforded by certain tables in the Board of Trade publications concerning the cost of living in English and German towns respectively. In the Blue-book dealing with England the real wages of
London, the Midlands and Ireland are calculated by means of index numbers, in which London (corresponding in our time index, say, to the year 1890) is taken as base, and the price of consumables and the rents prevailing there are both represented by 100. On this plan, prices of consumables and rents being given weights of 4 and 1 respectively, the Board of Trade found real wages in London to be equal to those of the Midlands, and 3 per cent higher than those of Irelands. If, however, Ireland had been take as base, the indices of real wages would have been in London 98, in the Midlands 104, in Ireland 100. A similar difficulty emerges in the Blue-book on German towns. The Board of Trade, taking Berlin as base, found real wages higher in that city than in any place save one on their list.
*79 “If the North Sea ports, instead of Berlin, had been taken as base, Berlin would have appeared fourth on the list instead of second, and the order of the other districts would have been changed; and, by taking Central Germany as base, even greater changes in the order would have been effected.”
*80 It is true, no doubt, that
large discrepancies of this sort are not likely to occur, except when there are large differences, or, as between different times, large fluctuations, in the prices of commodities that are heavily weighted. But that fact, though practically interesting, is not relevant to my present point.
§21. It may happen in some circumstances that we have no knowledge of, and no data for guessing, quantities for any of the years we wish to compare, and are, therefore, forced back, for the price index number involved in our measure, on a sample of price relatives alone without any weights at all. In these circumstances the preceding discussions make one thing quite clear. We must not construct our index by combining the price relatives in a simple arithmetical average, after the manner of Sauerbeck. The paradoxes to which that method leads are avoided if either the simple geometric mean—this will not work if the price of any of our commodities is liable to become nothing!—or the median of the price relatives is taken. Professor Fisher has an
interesting discussion of the comparative advantages of these two forms.
*81 Both are plainly inferior to the weighted formula of § 18, where the data required for that formula are available.
§ 22. In conclusion we have to consider the
reliability of the various practicable measures which are available as representatives of the full-data measure. Let us first suppose that we can obtain a sample of the same general form as the full-data measure, quantities as well as prices being available for both (or all) of the periods that we wish to compare. Five general observations may then be made. First, when the sample is drawn from most of the principal sets of commodities included in the full-data collection, which have characteristic price movements, the probable error of our measure will be less than it is when a less representative field is covered. Secondly, when the sample is large, in the sense that the expenditure upon the items included in it comprises a large part of the aggregate expenditure of our group upon the whole collection, the probable error is less than it is when the sample is small. With random sampling in the strict technical sense, the reliability increases as the square root of the number of items contained in the sample. Thirdly, when each of the items constituting the full-data collection absorbs individually a small part of the aggregate expenditure upon that collection, the probable error is less than when some of the items absorb individually a large part of the total expenditure. Fourthly, when the items included in the sample exhibit a small “scatter,” the various prices changing as between the years we are comparing in very similar degrees, the probable error is less than it is when the items exhibit a wide scatter. From this consideration it follows that the magnitude of the error to which our measure is liable is greater—apart altogether from the difficulty of “new commodities” referred to in § 14—as between distant years than as between years that are close together. The reason is, as Professor Mitchell, on the basis of a wide survey of facts, has shown, that the distribution of the variations in wholesale prices as between one year and the next is highly
concentrated,—more concentrated than the distribution proper to the normal law of error,—but the distribution of variations as between one year and a somewhat distant year is highly scattered. “With some commodities the trend of successive price changes continues distinctly upwards for years at a time; with other commodities there is a constant downward trend; with still others no definite long-period trend appears.”
*82 Finally, if we are unable to obtain a sample of the same general form as our full-data measure, and have to be content with one of the truncated form described in § 18, our measure will, of course, be less reliable than one of equal range of the better type. If we have to do without quantities altogether, and must use the simple geometric mean or the median of price relatives, the measure will be less reliable still. But, it is important to notice, the damage done to reliability by the use of an inferior index formula, like the damage done by the use of a small sample, is not very great when the scatter of price movements between the years we are comparing is small or moderate, but may be very great when the scatter is large.
h units means, not {(
x+
h)φ(
x+
h)-
xφ(
x)}, but
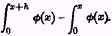
The Making of Index Numbers, appears to take the view that there is a way of making measures of this sort which is right in an absolute sense, and not merely in the sense that it will yield a measure consonant with the particular purpose which we want the measure to serve. Having examined a great many different sorts of index numbers, he found that, after those suffering from definite defects of a technical sort had been eliminated, the remainder, though formed on widely different plans, gave approximately equivalent results, and concluded: “Humanly speaking, then, an index number is an absolutely accurate instrument” (p. 229). Now, the close consilience of the results reached by different methods undoubtedly suggests to the mind that there exists somewhere an absolutely right result to which they are all approximating. But there is, so far as I can see, no real ground for accepting this metaphysical suggestion. Consider the analogy of a measure designed to ascertain the average height of a group of trees. It is easy to find the arithmetical, the geometrical, or any other average of their heights. In many conditions all ordinary forms of average will work out very nearly the same. But this is no proof that there is stored up in heaven an ideal average height different from these and, in an absolute sense, more accurate or truer than any of them. There is a true arithmetical average, a true geometrical average, a true harmonic average; but the concept of an archetypal avenge right in an absolute sense is, as it seems to me, an illusion. When we want to satisfy a given purpose it is proper to ask: will the arithmetical or the geometrical average best serve our purpose? If the two averages happen to be nearly the same, we are in the happy position that it does not much matter should we accidently choose the wrong one. But we cannot properly say more than this, There is some reason to believe, however, that, when Professor Fisher claims that the choice of the formula for a price index number is independent of the purpose to be served, he is using the term purpose in a narrower sense than mine, and would not disagree with what is here said.
minus an allowance for the part of the value of this machinery and plant that is used up in producing consumable goods during the year itself.
able to buy at the ruling price the quantity of any commodity which it wishes to buy at that price. When official maximum prices have been fixed, and people’s purchases at those prices are restricted, either by a process of rationing or by the fact that at those prices there is not enough of the commodity to satisfy the demand, this condition is, of course, not realised. During the Great War the situation was further complicated by the fact that the legal prices were often departed from—at least in Germany—in practice.
e.g. a tropical as against a polar region) than it is that one of the two neigbhouring places will purchase commodities that are not known in the other. As between distant places the chain method, about to be described, could theoretically be applied
via a chain of intermediate places; but practically this method of comparison would probably prove unworkable.
Contemporary Review, March 1887, p. 371, etc.
The Review of Economic Statistics, May 1921, p. 110.) But if, say, half the expenditure in 1920 is on commodities that did not exist in 1900, a chain comparison is no longer an inferior substitute for a direct comparison: it is the only sort of comparison that it is possible to make at all. For this reason it seems to me on the whole best that, in constructing
a series of index numbers, we should employ the chain method, and not the method of calculating a number for each year relative to one (the same) base year. In the absence of new commodities the issue would be balanced, because, whereas the chain method gives perfectly correct results only as between successive years, the other method—except with constant weight formulae, which are inadmissible on other grounds—gives perfectly correct results only as between the base year and each other year. But the argument from new commodities tips the scale in favour of chain series. Of course, if, having constructed a chain series, we desire a more special comparison between two years (other than successive years) covered by it, and if, as between those years, the “new commodity” trouble happens to be unimportant, it will be well to calculate a new number directly for this purpose instead of using the series number. (For Fisher’s view compare
The Making of Index Numbers, p. 308, etc.)
Bulletin of the U.S.A. Bureau of Labour Statistics, No. 173, pp. 66-7). This is quite correct as it stands, but it must not be interpreted to imply that both finished products and the raw materials embodied in
those same finished products should be included.
Contemporary Review, March 1887, p. 374.
Money, Credit, and Commerce,, p. 33.
Economic Journal, 1913, pp. 622-3.
priori expectations, coupled with the general form of our sample, show that the original distribution, from which the sample is taken, obeys some ascertained law of error. Whether they do this or not will often be hard to decide. It should be added that the practical effect of omitting extreme observations is only likely to be important when the number of commodities included in our sample is small; and that it is just when this number is small that adequate grounds for exclusion are most difficult to come by.
Economic Journal, 1908, p. 473.
The Making of Index Numbers, p. 211, etc., and p. 260, etc.
Part I, Chapter VII
