The Theory of Interest
By Irving Fisher
THE tremendous expansion of credit during and since the World War to finance military operations as well as post-war reparations, reconstruction, and the rebuilding of industry and trade has brought the problems of capitalism and the nature and origin of interest home afresh to the minds of business men as well as to economists. This book is addressed, therefore, to financial and industrial leaders, as well as to professors and students of economics.Inflation during and since the War caused prices to soar and real interest rates to sag in Germany and other nations far below zero thus impoverishing millions of investors. In all countries gilt-edge securities with fixed return became highly speculative, because of the effect of monetary fluctuations on real interest rates. After the War the impatience of whole peoples to anticipate future income by borrowing to spend, coupled with the opportunity to get large returns from investments, raised interest rates and kept them high. Increased national income has made the United States a lender nation. At home, real incomes have grown amazingly because of the new scientific, industrial, and agricultural revolutions. Interest rates have declined somewhat since 1920, but are still high because the returns upon investments remain high. Impatience to spend has been exemplified by the organization of consumers’ credit in the form of finance companies specially organized to accommodate and stimulate installment selling and to standardize and stabilize consumption…. [From the Preface]
First Pub. Date
1930
Publisher
New York: The Macmillan Co.
Pub. Date
1930
Comments
1st edition.
Copyright
The text of this edition is in the public domain.
- Dedication
- Errata
- Preface
- Suggestions to Readers
- Part I, Chapter 1
- Part I, Chapter 2
- Part I, Chapter 3
- Part II, Chapter 4
- Part II, Chapter 5
- Part II, Chapter 6
- Part II, Chapter 7
- Part II, Chapter 8
- Part II, Chapter 9
- Part III, Chapter 10
- Part III, Chapter 11
- Part III, Chapter 12
- Part III, Chapter 13
- Part III, Chapter 14
- Part IV, Chapter 15
- Part IV, Chapter 16
- Part IV, Chapter 17
- Part IV, Chapter 18
- Part IV, Chapter 19
- Part IV, Chapter 20
- Part IV, Chapter 21
- Appendix to Chapter I
- Appendix to Chapter X
- Appendix to Chapter XII
- Appendix to Chapter XIII
- Appendix to Chapter XIX
- Appendix to Chapter XX
- Appendix to Chapter XX
§ 1 (to Ch. X, § 2)
[Geometric representation of incomes for three years]
APPENDIX TO CHAPTER X
IF we proceed from the consideration of two years to that of three, we may still represent our problem geometrically by using a model in three dimensions. Let us imagine three
mutually perpendicular axes from an origin
O called respectively
OX‘,
OX”,
OX”’, and represent the income combination or income stream for the particular individual by the point
P, whose coördinates
c‘,
c”, and
c”’ are the three years’ income installments with which the individual is initially endowed. Then through the point
P draw, instead of the straight line in the previous representation, a
plane ABC cutting the three axes in
A,B, and
C. This plane has a slope with reference to the two axes
OX‘ and
OX” of
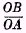 equal to
equal to
1 +
i‘ (unity or 100 per cent plus the rate of interest connecting the first and second years), and has a slope with reference to the axes
OX” and
OX”’ represented by
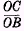 equal to
equal to
1 +
i” (unity plus the rate of interest connecting the second and third years). Now suppose the space between the axes to be filled with willingness
surfaces laminated like the coats of an onion, such that for all points on the same surface, the total desirability or wantability of the triple income combination or income position represented by each of those points will be the same. These surfaces will be such as to approach the three axes and the planes between them, and also such that the attached numbers representing their respective total wantabilities shall increase as they recede from the origin. The plane
ABC drawn through
P at the slope fixed by the rates of interest just indicated will now be tangent to some one of the willingness surfaces at a point
Q, which is the point at which the individual will, under these conditions, fix his income situation, for every point on the plane
ABC will have the same present value, and every point on this plane is available to him by borrowing and lending (or buying and selling) at the rates
i‘ and
i”, but not all of them will have the same desirability, or wantability. He will select that one which has the maximum wantability, and this will evidently be the point
Q, at which the plane is tangent to one of the family of willingness surfaces. This point will be such that the rates of time preference will be equal to the rate of interest.
So much for the individual. The market problem determining the rate of interest is here solved by finding such an orientation for the various
planes through the given points called
P‘s as will bring the center of gravity of the tangential points, the
Q‘s, into coincidence with the fixed center of gravity of the
P‘s.
To proceed beyond three years would take us into the fourth dimension and beyond. Such a representation cannot be fully visualized, and therefore has little meaning except to mathematicians.
