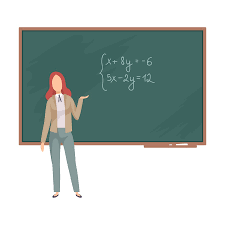
Some brief but straightforward algebra.
The part of my post yesterday that dealt with deadweight loss from taxes was a little brief. Even if you go to the original article in Defining Ideas, you won’t find the actual computation. So here it is.
DWL is is proportional to t^2, where t is the tax rate. (t^2 means t-squared)
Original tax rate for our high-income Californian is 54.1%.
New tax rate for our high-income Californian is 56.7%.
This 2.6-percentage-point increase is a 4.8% increase. (2.6/54.1 = 0.048, which is 4.8%.)
So why doesn’t the DWL increase by just 4.8%? Because of the square relationship I referred to in the article and above.
Let original DWL be DWL1. Because of the proportionality property, we can lump all the other components of DWL into C. C is the same whether we are dealing with the original tax rate or the new higher tax rate.
So DWL1 = C*t1^2, where t1 is the original tax rate.
DWL2 = C*t2^2, where t2 is the new tax rate.
To get the percent increase in DWL, first divide DWL2 by DWL1.
DWL2/DWL1 = C*t2^2/C*t1^2 = t2^2/t1^2.
t1 = 0.541; t2 = 0.567.
So DWL2/DWL1 = 0.567^2/0.541^2
= 0.321/0.293
= 1.096.
Therefore DWL increases by 9.6%. QED.

READER COMMENTS
William Connolley
Apr 5 2021 at 1:08pm
But *why* is DWL prop t^2? Is it empirical or theoretical?
David Henderson
Apr 5 2021 at 2:57pm
Theoretical and easy to derive. Check almost any public finance text.
Alan Goldhammer
Apr 5 2021 at 1:29pm
If California taxes are so onerous, why are you still living there? You are retired and not tied down to a job. Move to Texas like a lot of other Californians.
David Henderson
Apr 5 2021 at 3:00pm
Because life is about more than taxes.
I’ve successfully fought off increases in various earmarked taxes over the last 20 years because in order to pass, they must get 66.7 percent of the vote. I work to get the opposition from the low 30s to the high 30s. I’ve always realized that I didn’t need to win because I could handle any plausible tax increase they throw my way. I then realized that I’m working to help lower- and middle-income people, which is fine.
What gets to me about California more than taxes is the whole political environment. I do think Texas would be better. I don’t, however, want a divorce: I’m still madly in love with my wife.
Thomas McKay
Apr 5 2021 at 4:45pm
Here’s to along and happy marriage for you and your madly loved wife!
David Henderson
Apr 7 2021 at 10:50am
Thanks, Thomas.
Michael Rulle
Apr 6 2021 at 10:32am
“life is about more than taxes” ——True.
Is the DWL of taxes an accepted theory in economics? Or is it controversial. I have never heard of it—-one would have thought that would be an excellent political argument. T^2 seems huge. Why would we want any taxes? Does that apply only at the margin relative to a given tax rate?
Todd Moodey
Apr 6 2021 at 10:41am
DWL from taxation is mentioned in every introductory microeconomics textbook. You typically see a triangle representing the loss, which grows in nonlinear fashion as both the base and height of the triangle expand with a larger tax.
Michael Rulle
Apr 6 2021 at 10:52am
Thanks Todd. I never heard of it—-or forgot that I did! Question still is, how controversial is the idea—-for example, what are the mitigating arguments against no taxes?
David—-just read your other essays—-as I implied to Todd, it would seem to me that every economist would have this high on their list as to why we should eliminate taxes. I can imagine some equality or fairness arguments——I suppose. But for sure I have not read about this (even if I should have learned it in school) or ever heard about this in any public forum——before you wrote about it.
It does not matter if I ever heard of it—-what I really am asking is how is this not a major topic of policy discussions?
David Henderson
Apr 6 2021 at 11:37am
Todd answers your first question well.
So no, it’s not controversial.
As your second question–how is this not a major topic of policy discussions–I don’t have a good answer although it should be.
I do have a confession, though. When I put together The Fortune Encyclopedia of Economics, which later became The Concise Encyclopedia of Economics, I wanted an article that was a good overall mainstream treatment of taxation. I commissioned this one by Joe Minarik, who at the time was a major player on the Democratic side of the House of Representatives. I looked back at the article recently and was surprised that Joe didn’t even devote a paragraph to DWL. He implicitly mentions it with his treatment of efficiency and the importance of not distorting behavior, but he doesn’t mention DWL. That’s a failing on my part as the editor.
Todd Moodey
Apr 6 2021 at 11:41am
Michael–
I’ll defer to David of course, but the way I think about DWL is that it’s foregone economic activity in which the parties would have preferred to engage but for the imposition of the tax. In that sense, I don’t think it’s controversial. Whether such activity is worth sacrificing for whatever the tax funds is probably the controversial matter.
Todd
RRC
Apr 7 2021 at 9:07am
It is only proportional in a specific case, e.g. if the government imposes a tax rate of t and then they buy a lot of things with that which gets destroyed, then the welfare losses are not O(t^2), they are O(t).
In the other case, if the government, say, redistributes (e.g they tax one thing and subsidize another), then your welfare loss is O(t^2).
You’re implicitly assuming that the tax revenues are redistributed to the consumers and producers when saying proportional to t^2.
Comments are closed.