I hesitate to join the ranks of the abundant newly-minted amateur epidemiologists out there. But here goes.
I’ve heard many people claim that a population can’t reach herd immunity to any disease until 60-70% of the population has been infected. This is a grave overgeneralization; as this primer explains, the critical value for herd immunity directly depends on how contagious the disease is:
The critical value, or threshold, in a given population, is the point where the disease reaches an endemic steady state, which means that the infection level is neither growing nor declining exponentially. This threshold can be calculated by taking R0, the basic reproduction number, or the average number of new infections caused by each case in an entirely susceptible population that is homogeneous, or well-mixed, meaning each individual can come into contact with every other susceptible individual in the population,[9][29][42] multiplying it by S, the proportion of the population who are susceptible to infection, and setting this product to be equal to 1:
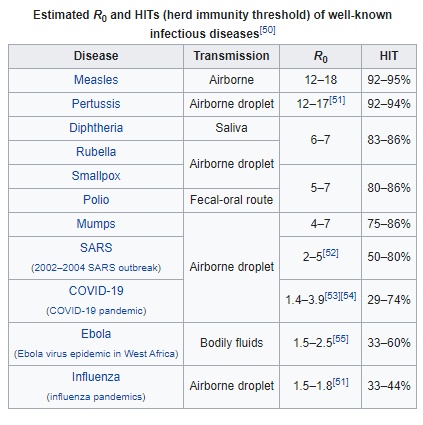
Thus, since measles is ultra-contagious, you don’t reach herd immunity until over 90% of the population is immune. The critical value for flu, in contrast, is barely one-third of that. Estimates of the critical value for COVID-19 range from 29-74%. Check out this table.

The standard way of boosting immunity, of course, is vaccination. As vaccination goes up, S goes down – and society moves toward herd immunity. Yet in principle, anything that reduces susceptibility to contagion has the same effect. If people wash their hands more, that effectively reduces S. If people socialize less, than reduces S. If people stop shaking hands, that reduces S. If people live in a low-density area, that reduces S.
Critically, all of these defensive factors multiply. If washing your hands more, socializing less, ending handshakes, and living in West Virginia each reduces S by 2%, then doing all four reduces S to .98^4=92.2% of its original value. It’s the same as the logic of contraception. Suppose you use birth control pills, condoms, withdrawal, and 50% abstinence. Your probability of pregnancy equals your base probability, multiplied by the failure rates of all four methods.
Some of my friends overrate R0, imagining that getting R0<1 prevents full infection of the population. But with a finite population (i.e., any actual population), you can infect everyone with an R0 far below 1. Suppose your society has 15 people, and 10 are already sick. Then even with R0=.34, all 15 people eventually catch the disease. After all, the infinite sum of 10 + .34*10 + .34^2*10+…=10/(1-.34)>15.
That’s the bad news. The good news is that infection and vaccination are only the two best-known ways to effectively shrink S. An endless list of behaviors are not only on the shelf, but are already in play. Paid voluntary human experimentation would help us find the low-hanging behavioral fruit in a matter of weeks, but at least almost everyone today bases their precautions on germ theory rather than witchcraft.
Additional good news: Fatality rates vary dramatically by age and even more dramatically by health status. So once you multiply the effect of all forms of mitigation to figure out when we’ll hit herd immunity, you shouldn’t mechanically multiply that by the average infection mortality rate to estimate total deaths. As Dan Klein puts it:
Let’s look at Wikipedia’s definition of herd immunity. It is based on a threshold condition where the still-susceptible proportion of the population multiplied by R0 equals 1.
What is R0? It is “the average number of new infections caused by each case in an entirely susceptible population that is homogeneous, or well-mixed” (Wikipedia, italics added).
Well-mixed is what we strive to prevent! We strive to separate the vulnerable from the rest of the population.
I’m not so optimistic about the “we” part. But you can definitely do so. If you’re vulnerable, take high precautions. If you’re not vulnerable, give the vulnerable their space.
P.S. Yes, you could just as easily say that behavior affects R0 rather than S, but I thought my way was a bit clearer.


READER COMMENTS
Philo
May 21 2020 at 11:53am
It seems that the R0 and S concepts are not very useful except when the population is, in fact, homogeneous and well-mixed, which the U.S. population and the population of the whole world are not.
Greg Hamer
May 21 2020 at 1:36pm
The arithmetic and the English check out but it does not leave the impression that four factors that indecently reduce susceptibility 2% result in a susceptibility reduction of 7.8%. That result does not sound like it is worth all the words. Instead on first reading it sounds like you are claiming a 92.2 percent reduction.
mark
May 25 2020 at 8:54am
It does matter more the more factors we have and the higher their probabilities are. Hand-washing, wearing masks, living in a village, no-longer-going in restaurants or other closed room with many persons, taking the recommended dose of Zinc and vitamin D (not more), vaping nicotine, living alone, driving alone, home-officing, online-shopping – see, the lists can go long. And some of those factor reduce the chance for infection (or mortality) by much more than 2%, I hope. If you add them up, they may reach easily over 100%. But multiplying may leave you with just a 60% reduction. Or 20%. Real trouble is, we have not much an idea what percentage to apply to each factor. Normal masks may be just decorative, Nicotine a fluke (France: 28% smokers, but just 8% of covid-cases smokers , source The Economist ), Hand-washing and even 6-foot-distacing much less important (Prof. Drosten ) as mostly via airborne infection in rooms, buses, hospitals – aerosoles.
John Alcorn
May 21 2020 at 2:03pm
The standard phrase, “herd immunity,” muddies the waters, insofar as non-experts naturally—but mistakenly—take the phrase to mean:
(a) The group is immune;
or
(b) Uninfected persons in the group can’t get infected if x% of individuals in the group have been infected, have recovered, and have acquired immunity.
My intuition is that experts should use the technical term, “endemic steady state.” Bryan Caplan reminds us that adaptation is one of the factors that set the threshold of a group’s endemic steady state.
A colloquial translation for this adaptive steady state might be, “stable percentage of immune persons, given our policies, practices, technologies, and demographics.”
People in a group (say, a nation) are keen to know:
(1) Given such-and-such policies, practices, technologies, and demographics, what percentage of individuals must have immunity for the group to have a stable percentage of immune persons?
(2) What are the residual risks of infection for those who are still susceptible?
Libertarians and Swedes are keen to rely on mostly voluntary (private) adaptation, along with excellent public-health information, strong norms of self-isolation (with temporary stipend) for symptomatic persons, and keyhole solutions for the vulnerable (esp. the elderly or frail). Robin Hanson and other advocate also experiments in voluntary variolation with temporary isolation and medical supervision.
Bryan writes:
Well, “anything” includes also lockdown (shelter-in-place), shutdown (closures), and surveillance-and-quarantine regimes (screen-test-trace-isolate).
Many experts, authorities, and citizens believe that coercion and suspension of privacy can and should be part of a stable regime of policies and practices until effective treatments or vaccines will be developed.
In principle, New Zealand and Taiwan might achieve a stable percentage of immune persons at close to zero.
I’m not making predictions. And I favor Sweden’s policy. (I have skirmished repeatedly with Scott Sumner.) My point is that the concept of an adaptive steady state doesn’t preclude coercive or invasive policies. It’s an empirical question, which adaptations (policies, practices, technologies) achieve stable prevalence, at what level.
Speed
May 21 2020 at 5:51pm
Caution! R0 is not an easily measured value like the freezing point of distilled water at pressure. Rather …
Complexity of the Basic Reproduction Number (R0)
https://wwwnc.cdc.gov/eid/article/25/1/17-1901_article
A Country Farmer
May 22 2020 at 10:40am
Latest metastudy on fatality rates: https://www.medrxiv.org/content/10.1101/2020.05.13.20101253v1.full.pdf
John Alcorn
May 23 2020 at 4:20pm
Compare a new study of thresholds of “herd immunity” (endemic steady state) in Stockholm county, Sweden: P. V. Brennan & L. P. Brennan (U. College London), “Susceptibility-adjusted herd immunity threshold model and potential R0 distribution fitting the observed Covid-19 data in Stockholm” (19 May 2020). The authors write:
The authors emphasize two mechanisms—(a) individual and social heterogeneity in R0 and (b) incomplete mixing—that lower the threshold of an endemic steady state, i.e., the threshold of a stable ratio of immune persons to susceptible persons in the populace.
In the case of Stockholm County, I would emphasize also another set of mechanisms that lower the threshold of an adaptive endemic steady state; namely, behavioral adaptations in light of trusted communications from public-health authorities. Hygiene (hand-washing), self-isolation of symptomatic persons, and voluntary social distancing have been key private adaptations in Stockholm County. These mechanisms modify heterogeneity and mixing, and thereby help to lower the threshold of an endemic steady state.
Jose Pablo
May 24 2020 at 4:49pm
I will be very careful when talking about an “average value” for R0. With all the risks of “joining the ranks of newly-minted amateur epidemiologists”, very likely the R0 of an individual has a probability distribution. If this distribution has fat tails (which could be the case), the “average” R0 is meaningless and what we should be worried about is the full probability function and, in particular, the very size of this fat tails.
Mark Z
May 24 2020 at 5:19pm
It’s often said these days that the average R0 is meaningless, which isn’t really true. If 9 out of 10 people who get a disease don’t pass it on, while 1 out of 10 passes it on to 5 people, then the disease will gradually disappear as it would if each of the 10 passed it on to 0.5 people. The fat tail of the distribution has severe implications about what the best ways (or what ways are possible) to reduce the average rate, which isn’t really the same as rendering it meaningless as a measure.
Jose Pablo
May 30 2020 at 3:49pm
Not quite Mark. For any value of R0, even below zero, you still have probabilities of having major outbreaks and the probability of this being the case, depends on the complete “shape” of the Ro distribution and, in particular, the presence of “superspreaders” (both people and events) that configure this R0 “fact tail”.
Having a R0 distribution with a lower average but a higher kurtosis can be “worse” (has a significant probability of being worse) that having an Ro distribution with a higher average but a lower kurtosis.
R0 can have a distribution that is not properly capture by its average value (not even close to it).
Comments are closed.