The Power to Tax: Analytical Foundations of a Fiscal Constitution

Constraints on Base and Rate Structure*

In constraining any system of government, and fixing the several checks and controls of the constitution, every man ought to be supposed a knave, and to have no other end, in all his actions, than private interest.

—David Hume, "Of the Independency of Parliament,"
Essays, Moral, Political and Literary, pp. 117-18

As we have noted, traditional normative tax theory applies external criteria for economic efficiency and equity to evaluate alternative taxing arrangements. In the standard comparisons among alternatives, the problem is posed in equi-revenue terms. Government is presumed to require some exogenously determined amount of revenue per period, with the analysis having as its purpose the identification of that taxing arrangement that will generate such revenue most effectively as measured against the criteria chosen. In all essential respects, the standard analysis is institutionally vacuous. No attention is paid to possible feedback effects that specific tax instruments may exert on government itself in determining how much revenue it seeks to raise. By contrast, such possible interdependencies between the form of tax instruments and the behavior of governments in demanding revenues become central to any constitutional approach, including specifically one in which a Leviathan model of governmental process is adopted.*33

To emphasize the dramatic difference that the change in assumptions about political process makes, it will be useful to summarize the "principles" for tax structure that emerge from the orthodox analysis. As noted, government is implicitly assumed to require a fixed amount of revenue per budgetary period, an amount that presumably will finance some efficient or optimal quantity of public goods and services, considered independent of the spending side of the account. In this framework, the ideally efficient tax is taken to be the lump-sum levy which, by definition, exerts no behavioral influence.*34 Since persons do not adjust their behavior in any way in response to the tax, there can be no excess burden, no inefficiency that is tax-induced. Furthermore, within groups of taxpayers that are biologically homogeneous (with respect to features that cannot be modified by behavioral adjustment, features such as age, sex, race, and measured natural capacities and skills), the lump-sum tax must be uniform over separate persons. Hence, the central criterion of horizontal equity, equal treatment for equals, is satisfied along with that of economic efficiency.

The lump-sum tax serves as an analytical benchmark in the orthodox normative theory despite the widespread acknowledgment that it does not exist in practical reality. When it is recognized that all taxes must exert some behavioral influence, efficiency and equity criteria may come into conflict in the evaluation of alternative arrangements. On strict efficiency grounds, separate persons should be taxed in accordance with their separately predicted behavioral responses. Overall, excess burden is minimized only when the least responsive persons are taxed more heavily than are those who are more responsive. In such a case, however, equals, as measured by pretax situations, may not be treated equally, and equity considerations dictate uniformity of treatment regardless of behavioral response. Similarly, equity considerations may suggest relative differences in the tax treatment of "unequals" that run counter to the requirements for strict economic efficiency. If, for example, persons at lower ranges of the income or wealth scales should prove to be less responsive to tax than persons at the upper ranges, efficiency norms would suggest regressive rate schedules. Only such schedules would minimize excess burdens in this setting. However, equity norms might indicate that regressive rate schedules should be rejected out of hand and that persons should be confronted with rates that are at least proportional or possibly progressive in relation to pretax measures of tax base.

This orthodox normative evaluation of the characteristics of tax structures depends critically on the equi-revenue postulate, one that is untenable when we substitute a revenue-maximizing government for the passively benevolent politics implicitly assumed in the standard treatment. At the constitutional stage of decision in the Leviathan model, potential taxpayers will recognize that government may be held back in its fiscal appetites only by limits on tax bases and on allowable rate structures. Even the analytical benchmark, the idealized and abstract lump-sum tax, loses its "efficiency" features in constitutional perspective.*35 If indeed a tax could be located that exerts no behavioral influence, and if a revenue-maximizing government should be granted access to such a source of funds, all persons would be totally vulnerable to the fiscal authority, with all potential economic value subject to overt confiscation in the taxing process.

As actual tax institutions rather than the idealized models are evaluated, the constitutionally derived efficiency ranking becomes quite different from that which emerges from the orthodox equi-revenue comparison. By contrast, the constitutional perspective tends to be consistent with and hence to reinforce the equity norms that emerge from the more limited, and more naive, orthodox discussion. The principle of horizontal equity, equal treatment for equals, or, put simply, uniformity of treatment for similarly situated persons, becomes a feature of any tax structure that can begin to constrain Leviathan's exactions. If government is constitutionally required to follow precepts of generality in its fiscal dealings with citizens, the revenue potential that could possibly be derived from sophisticated discrimination among separate persons and groups of taxpayers is foreclosed.

Much the same conclusion arises with respect to rate schedules that confront the potential generators of tax base. If we make the plausible assumption that the potential taxpayer secures diminishing relative marginal utility from generating taxable base, whether this base be money income, money outlays, or specified items of spending or earnings, it follows that government can maximize revenue collections only by imposing an ideally regressive tax-rate schedule. Hence, a constitutional constraint against regressive schedules can serve to limit government's taxing power, defined in gross revenue terms. Note that the requirement for uniformity or generality in tax treatment among persons as well as the possible requirement that rate schedules be nonregressive become possible characteristics of an efficient "tax constitution," quite apart from any explicit introduction of external norms for tax equity or tax justice.

Over and beyond constitutional constraints on rate schedules, some limitations on the allowable bases for tax may be desired. In the orthodox normative theory, comprehensiveness in the actual bases of a tax is a highly ranked attribute of a fiscal structure. The logical support for such comprehensiveness is straightforward. To the extent that individuals, as potential taxpayers, are allowed to shift from taxable to nontaxable options, excess burden arises which represents deadweight loss to the community. Furthermore, to the extent that some potential taxpayers shift into nontaxable options while others do not, inequities seem to be created. Within an equi-revenue frame of reference, the argument for comprehensiveness in tax base is valid. But in the constitutional perspective taken in our analysis, the traditional support for tax-base comprehensiveness disappears.

Our purpose in this chapter is to examine in somewhat more formal terms the revenue-maximizing model of government and to analyze possible tax-base and tax-rate constraints that will serve to keep fiscal excesses within tolerable limits.

3.1. Government as Revenue Maximizer Subject to Constitutional Tax Constraints

As Knut Wicksell noted, no persons would approve the imposition of taxes, either at a constitutional or a postconstitutional stage of decision, unless they anticipate securing some benefits from the goods and services that they expect government to finance with the tax revenues collected. Taxes are coercive instruments that allow governments to levy charges on persons without any corresponding expression of current willingness to pay. Furthermore, even in the most effective models of political democracy, the consent of only a majority of the members of a representative assembly is needed for tax legislation.

Perhaps at one period in history it may have seemed reasonable to rely on the operation of majority rule in legislatures to hold governmental fiscal activities in bounds. And, of course, majority-rule models remain in formal theories of collective decision making and in popular discussions of democracy. However, confronted with public sectors of modern scope and bureaucracies that demonstrably possess power quite apart from specifically legislated authority, the democratic-limits model of governmental fiscal restraint becomes increasingly naive. Some of the reasons for questioning the efficacy of electoral constraints were discussed in Chapter 2. A more acceptable model for rational constitutional choice would seem to be one in which the political-bureaucratic process, as it is predicted to operate postconstitutionally, involves the maximization of revenues within tax constraints that are imposed through the fiscal constitution.

Such a model of political process, one that may be termed a model of Leviathan, has been introduced in Chapter 2. The citizenry has no effective control over government, once established, beyond the constraints that are imposed constitutionally. It is assumed that such constraints are binding, but that postconstitutional or in-period fiscal decisions within these constraints are made entirely by the budget-maximizing or revenue-maximizing politicians-bureaucrats.*36

Our stylized constitutional choice setting is characterized by the further and familiar assumption that each person has well-defined predictions about the aggregate level and the distribution of incomes and consumption patterns in all postconstitutional periods, but that he possesses no knowledge about his own future position within the distribution or about the characteristics of his own taste pattern.*37 The general, nonindividualized knowledge is sufficient to allow the person to make some estimate, within broad limits, both of the "efficient" levels of budgetary outlay on public goods, and of the aggregate revenues that might be obtained under alternative tax arrangements. Since the individual remains ignorant concerning his own predicted income or tastes, he cannot identify a cost share for himself under any particular tax system. He cannot, therefore, predict whether, postconstitutionally, he might prefer a larger or a smaller public-goods quantity than that which he predicts would be "efficient" for the whole community. Hence, each individual, rationally, will prefer institutions that generate roughly the "efficient" quantity, 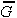, given an independent estimate of the costs of provision. The actual outlay on desired public goods and services is defined by

G = aR,

(1)

where a is the predicted proportion of tax revenue spent on actually providing goods and services desired and R is aggregate tax collections or revenues. Throughout the analysis of the model to be discussed in this chapter, the value for a will be taken to be exogenous, by which we mean that it is fixed by the operation of constraints other than those here analyzed.*38 As we have indicated, a is such that

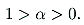(2)

Hence, the outlay on desired public goods and services is some direct function of total revenue raised, and the problem that the individual faces at the constitutional stage is to organize tax arrangements so that the revenue raised, when adjusted by a, will yield the quantity of public goods and services estimated to be "efficient" at the given estimated new costs—costs that will, of course, be dependent on the value of a.*39 Thus, R will be chosen so that

aR = .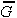

(3)

The characteristic assumption of the Leviathan model is that, in each postconstitutional budgetary period, government will attempt to maximize total revenue collections (and hence total spending) within the constitutionally appointed tax regime. That is, government will make

R = R*(b,r),

(4)

where R* is the maximum revenue that can be raised from the tax regime and is a function of b, the tax base, and r, the allowable rate structure to be imposed on this base. Formally, the problem facing the individual at the stage of constitutional choice is to select b and r so that

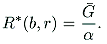(5)

3.2. Tax-Base and Tax-Rate Constraints in a Simple Model

Initially, we restrict the analysis to a single individual who is assumed to be exercising his constitutional choice between only two potential definitions of the tax base—one that is fully "comprehensive" and another which falls short of this limit. We shall relax these assumptions later, but at this point the simplification is convenient. It is immaterial for our argument precisely what the noncomprehensive base is and whether the tax is levied on the "uses" or the "sources" side (i.e., whether it might be an income tax or an expenditure tax). Let us consider a simple model in which labor is the only factor of production. Suppose, further, that the noncomprehensive tax base is money income derived from labor effort in the market, and that the comprehensive base includes such money income and also the imputed money equivalent of the individual's nonmarket production of valued end products, including leisure; in other words, the comprehensive base is full income or potential income. The question to be examined is whether the person would prefer a tax constitution that embodies the comprehensive base over the one that restricts the base of tax to money income.*40

Figure 3.1

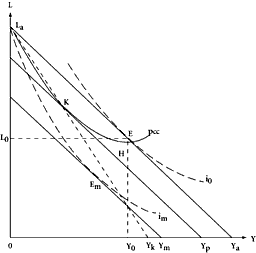
The situation may be depicted as shown in Figure 3.1. The indifference curves, labeled with i's, indicate the individual's preferences as between money-income-earning activity, Y, and, say, leisure activity, L. These preferences exhibit the standard properties.*41 As is customary in orthodox tax analysis, in this introductory discussion we ignore income-effects feedbacks generated by the provision of public goods. The pretax situation is characterized by a relative trade-off between L and Y that reflects the productivity of income-earning activity. The initial pretax equilibrium is at E (Y₀, L₀) on i₀.

Consider next the prospect that the individual would face if the government acquires access to the fully comprehensive tax base. In such an event, the individual would be exploitable up to the full limits of his potential income-earning ability over and beyond some minimal subsistence. Apart from this minimum, all of the "income equivalent," 0Y_a, is potentially available for governmental use. The government bent on maximizing revenue could levy a tax that expropriated the individual's maximum potential earnings beyond the allowed subsistence level.*42

Since it is inconceivable that anyone could ever anticipate an "efficient" public-sector-private-sector mix that would require all potential income above subsistence for governmental purposes, it seems clear that a potential taxpayer-beneficiary would not select the comprehensive tax base if he predicts postconstitutional governmental behavior of the type that we have postulated. He will seek instead to impose constitutional constraints on the fisc, on the ability of government to tax. He can do so, in our simple case, by allowing the government to levy an income tax only on the ordinary sources of earnings—only on money incomes. The maximum revenue that can be secured from this narrowed tax base is depicted by Y_mY_a in Figure 3.1. Clearly, if the government imposes a tax on money income with revenue in excess of Y_mY_a, the individual would be better off by ceasing to earn income at all; he would improve his position by switching to position L_a. If limited to the money-income base, therefore, the government can secure revenues only up to this new maximum limit, Y_mY_a, and it can secure this amount only if it levies an "ideally" structured regressive tax, in which the rate for each level of Y is equal to the slope of i_m. This would involve creeping down i_m to the maximum revenue equilibrium shown in the limit at E_m, allowing the taxpayer a minute slice of surplus to ensure that his final equilibrium in the neighborhood of E_m is preferred to L_a.

Recognizing this prospect, the potential taxpayer may wish to impose the further constitutional constraint that the rate schedule should not exhibit regressivity. This choice would clearly emerge if the money-income base, together with the predicted value for a and the revenue-maximizing regressive rate schedule, should be predicted to generate outlays on desired public goods and services in excess of predicted efficient levels of provision. If, for example, the government should be required to stay within the confines of a rate structure that exhibits proportionality, at the least, it would effectively be confronted with a locus of potential equilibria along the individual's "price-consumption" curve for varying "prices" of Y, depicted by L_aKE in Figure 3.1. The revenue-maximizing arrangement in this case is shown where a line drawn parallel to L_aY_a is tangent to the price-consumption curve, indicated at K, with the associated revenue-maximizing proportional rate of tax on Y being Y_kY_a/0Y_a, and the revenue collected being Y_pY_a. The precise characteristics of this case and the analytic resemblance to familiar results in price theory can be isolated by appeal to the corresponding partial equilibrium diagram shown in Figure 3.2.*43

Figure 3.2

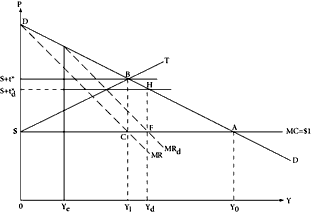
Curve DD in Figure 3.2 indicates the individual's demand for the income-yielding activity; this curve might be derived from a preference mapping exhibiting the properties depicted in Figure 3.1. Confronted with the requirement that it must levy a proportional tax, what tax rate will the revenue-maximizing government select? The question is clearly analogous to that asked about the behavior of the monopoly firm that seeks to maximize profits, with the same answer. We derive a "marginal revenue" curve, MR, in Figure 3.2, and the quantity of Y at which revenue is maximized is determined by the intersection of this curve with the horizontal dollar-price line (which is marginal cost), indicating a posttax equilibrium level of money income at Y₁ and a revenue-maximizing tax rate of t*. (Note that, when evaluated in the money-income numéraire, the cost of earning a dollar of income is simply a dollar. The "consumer's surplus" area between the demand curve and the cost curve in Figure 3.2 measures the utility value of money income relative to that of leisure, again evaluated in the numéraire, over and above that of leisure.)

The construction reveals the precise analogy between our model of postconstitutional governmental process and monopoly theory—in an analytic as well as a conceptual sense our model is appropriately designated a "monopoly theory of government." The revenue-maximizing tax rate, t*, can be derived algebraically as follows. We know that R = tY₁, where t is the proportional tax rate and R is tax revenue. Further,

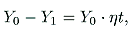
since

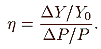(6)

and DP/P = t. Therefore,

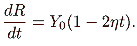(7)

and differentiating,

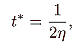(8)

Setting (8) at zero, we have

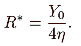(9)

and substituting t* in (7), we have

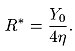(10)

Hence, as we might expect, maximum revenue is directly related to the initial size of the taxable base and inversely related to the value of the elasticity coefficient.

As we have indicated, the revenue raised from the given base under a proportional tax is less than that which might be raised under an ideally regressive rate structure. We are then led to ask what might be the influence of a progressive rate structure on revenue. In its dealings with a single taxpayer, the revenue-maximizing government will have no incentive to shift from the equilibrium proportional rate to any rate structure that embodies progression, since this latter would imply increasing rather than declining marginal rates of tax with income. The revenue effect can be demonstrated most easily by thinking of the simplest of all progressive rate structures, one that involves only two marginal rates, with the first being zero. Consider such a structure, sometimes called a degressive one, where income over some initial range, Y_e, is wholly exempted from tax. With this additional constraint, the revenue-maximizing proportional rate on remaining units of income falls and total revenue collections fall correspondingly.

Diagrammatically, this result can be indicated by drawing the new marginal revenue curve, MR_d, over the range where the nonzero proportional rate is to be applied—as in Figure 3.2, with the maximum rate being t_d*, with equilibrium total income at Y_d. Observation of Figure 3.2 reveals that the revenue-maximizing degressive structure generates less total revenue than under the strict proportional tax and, also, that the excess burden is smaller. Under proportionality, the excess burden is measured in Figure 3.2 by the area ABC. Under the postulated degressive structure, excess burden falls to AHF.

Not all forms of progression yield this result for the change in excess burden. For example, a linear progressive rate schedule (of the form shown by line ST in Figure 3.2) will yield a revenue-maximizing marginal rate, t*, that is equal to the revenue-maximizing proportional rate, with the same posttax equilibrium income at Y₁. Note that, in this case, the total revenue obtained under progression is a constant share of that which would be obtained under proportionality where the marginal rate levied at income Y₁ would be applied over the entire income range. Hence, under the rate structure, ST, total revenue raised under progression is one-half that raised under proportionality. Note that the excess burden in the two cases is identical.

It may be useful to summarize the basic arguments of this section. We have observed that the constitutional decision-making calculus of the taxpayer-beneficiary, operating under the expectation of a Leviathan-like postconstitutional fiscal process, involves his opting for institutional devices that will limit the revenue-raising potential of the tax system. We have explored in some detail two ways that might accomplish this purpose. One is by limiting the size of the tax base—increasing the size of the tax base will be, beyond a point, clearly undesirable. The other is by imposing constitutional constraints on allowable rate structures on any given base. These constraints may rule out the imposition of regressive rate schedules. The argument stems, of course, both from the constitutional perspective within which our whole analysis is developed, and from the unconventional, but uncomfortably plausible assumptions that we have made about the predicted working properties of the political process.

3.3. One among Many

In the simple model analyzed in the preceding section, attention was focused on the single individual's choice calculus. This model need not be nearly so restrictive as it might appear, since we have examined choice in a constitutional setting, where the chooser is not expected to know just what his own position will be in subsequent postconstitutional periods. Nonetheless, we have neglected the problems that arise when the individual recognizes that, regardless of what his own position might be, he will be one among many taxpayers, with differences in public-goods preferences and in tax-base characteristics.

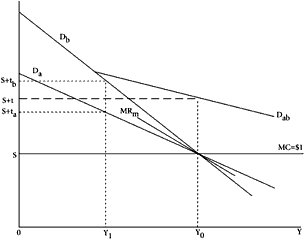Figure 3.3

We may first consider whether or not our earlier results concerning tax-base limitations will hold in this setting. We may look at a highly simplified two-person illustration. In Figure 3.3, we assume that two persons, A and B, will earn identical amounts of money income in some pretax or no-tax equilibrium, in the amount Y₀. (Recall that, under our constitutional-stage assumptions, the individual will know only that the two persons will have the characteristics depicted; he will not know which of the two positions he will personally occupy.) The two persons are predicted to differ substantially in their response to the imposition of a tax on the limited or money-income base, with leisure (and/or other valued end products) exempted from tax. This differential responsiveness is indicated by the slopes of the "demand curves" for money income, as shown by D_a and D_b.

The first point to be noted here is that so long as any responsiveness at all is predicted, the argument for the noncomprehensive base developed earlier holds without qualification. Each of the two persons whose preferences are depicted in Figure 3.3 will be protected against the exploitation potential of government that would be present under the full income as opposed to the money-income tax scheme.

Let us now examine the revenue-maximizing government's predicted taxing behavior in this two-person situation. If the government could treat A and B differently, and separately, and if it could levy a proportional tax on the money income of each person (we assume that a regressive schedule is not allowed), it would impose a tax rate of t_a on A and a rate of t_b on B. This sort of differential treatment would, under almost all circumstances, allow scope for the extraction of more revenue from the community than would be possible if the government were constitutionally required to levy the same proportional rate on each person, or, stated more generally, to confront each person with the same rate structure or schedule.

On the assumption that positive revenue is extracted from both persons in the uniform-rate case, that uniform rate will lie strictly between t_a and t_b (t_b > t > t_a). The revenue-maximizing uniform proportional rate, t, is determined in Figure 3.3, where the "market" marginal revenue curve, MR_m, cuts the dollar-price line, with "price" set at the intercept of the vertical drawn from this intersection and the aggregate "demand curve," D_ab.

As suggested in the introduction to this chapter, the requirement that all persons in the community be confronted with the same tax-rate schedule, or, in other words, that persons be treated uniformly, becomes an institutional means of reining the revenue-seeking proclivities of Leviathan. Such an argument for uniformity, which is related to but different from the more familiar "horizontal equity" norm, has not, to our knowledge, been developed in normative tax theory. With respect to horizontal equity, it is perhaps interesting to note that no constitutional rationalization for this principle, per se, emerges from our analysis.

The construction in Figure 3.3 can also be used to illustrate a proposition that seems at variance with that reached in models that assume institutional fixity. In the latter conventional framework, the behavior of individuals within the structure of given tax institutions is analyzed, and any attempt on the part of one person or group of persons to avoid or to reduce tax payments, through recourse to nontaxable sources or uses of income, is interpreted as imposing an external cost or diseconomy on less responsive taxpayers and/or on public-goods beneficiaries.*44 Behavior in reducing tax liability generates costs for others in the community by making higher rates of tax and/or lower rates of public spending necessary than would otherwise be required.

But now consider the same issue in our constitutional framework. An individual seeks to limit the revenue potential of Leviathan, while remaining uncertain as to his own position. In such a case, he is benefited by the fact that at least some taxpayers in the community will be able to reduce tax liabilities by shifting into nontaxable options because this will lead to a lower revenue-maximizing uniform tax rate. This result may be shown easily, as in Figure 3.3. Compare the revenue-maximizing uniform rate, t, with that rate which would be revenue-maximizing if the two taxpayers were predicted to be equally responsive in the manner indicated by D_b. The uniform rate would rise to t_b, with higher revenue collections by government. Therefore, B benefits by virtue of the fact that A responds along D_a rather than D_b, thereby ensuring that the tax rate is t, not t_b. To the extent, therefore, that a person in constitutional choice predicts that some members of the whole set of taxpayers will be able to shift to nontaxable sources or uses of income in postconstitutional periods, his own concern about the fiscal exploitation of Leviathan is correspondingly reduced.

As a final point in this section, we want to consider whether or not our earlier result concerning the relationship among progression, proportionality, and maximum revenue holds in the many-person setting. Recall that, in the one-person setting, the introduction of any progressive features into the tax-rate schedule would tend to reduce the potential maximum revenue that government might extract from the single taxpayer. The problem in the many-person setting becomes much more complex because both the differing behavioral responses and the differing pretax levels of income must be taken into account, within the requirement that uniformity in tax treatment be preserved. Recall that, in the simple two-person setting depicted in Figure 3.3, t_b > t > t_a, where t_a and t_b were revenue-maximizing proportional rates upon the two persons treated in isolation from each other, and where t was the revenue-maximizing proportional rate uniformly imposed on both persons. Can total revenues be increased above those raised by rate t if government is allowed to or required to introduce progression? By lowering the rate over some initial ranges of income, revenue collections from A, the most responsive person, will increase. But offsetting this increase in collections from A, there must be, over this range of incomes, a reduction in collections from B, who must be treated uniformly. Beyond this limit, however, collections from B may be increased by setting some rate above t. Whether or not the increase in revenue collections exceeds or falls short of the decrease clearly depends on the relative elasticities of the two persons' "demand curves" where they cut the horizontal at s + t, the revenue-maximizing proportional rate of tax. If the person designated as A in Figure 3.3 is much more responsive to the reduction in tax below t than B is to the increase in tax above t over the higher income ranges, progression may increase revenues above those raised by uniform proportionality. In other cases, this increase may not be possible.*45 The limitations imposed by dealing with a two-person model should be stressed here. What is of importance is the tax-adjustment elasticities of different groups of taxpayers. In terms of the representation in Figure 3.3, the addition of a third person equivalent to A would increase the likelihood that progression would be revenue-enhancing. On the other hand, adding a third person equivalent to B would reduce such a prospect. This result suggests that the relative revenue-generating properties of revenue-maximizing proportional and progressive rate structures depend critically on the distribution of taxpayers among the separate response groups, with separate levels of taxable income.

3.4. Tax Limits and Tax Reform

We have argued that the bases for taxation, as well as the rate structure, will be constrained constitutionally by the person empowered to choose among tax arrangements who does not know his own position and who adopts a revenue-maximizing model for the behavior of government in postconstitutional periods. Our analysis provides support for the noncomprehensiveness of the allowable tax base. To the extent that activities which yield value to taxpayers remain outside the allowable reaches of the fiscal authority, the appetites of Leviathan are checked. Persons may resort to nontaxable options, and in the knowledge that they will do so, government necessarily curbs its revenue extraction.

The danger of allowing government access to revenue-raising instruments that generate budgets in excess of those necessary for financing some roughly efficient levels of public goods and services has been central to our model. We should, however, recognize that constitutional tax constraints might, through time, prove to be overly restrictive. In this case, postconstitutional pressures will surely arise for escape through constitutional-style adjustments designed to widen the bases and to allow for more flexible rate structures, to move generally from specificity to comprehensiveness. Empirically, it will always be difficult to distinguish between genuine constituency demands for a relaxation of such constraints and the ever-present demands of the revenue-seeking politicians-bureaucrats. For the latter group, and for their spokesmen, efforts will tend to be directed toward widening bases, toward increasing the number of sources upon which taxes may be imposed. "Tax-reform" advocacy on the part of the "bureaucratic establishment" will tend to be centered on "tax-base erosion." Indeed, one indirect test of the empirical validity of our model of the political process lies in the observed lack of reformist concern about relative rates of tax within tax-law limits that currently exist.

In the discussion of proposed tax-base changes, the attitudes of the traditional normative tax theorist and the members of the taxpaying public differ more sharply than anywhere else. Our analysis is helpful in "explaining" the attitudes of the taxpayers. For example, they are likely to react negatively and emphatically to proposals to move toward taxation on the basis of full income, as, for example, by including the imputed rental values of owned residences in the base for personal income tax. The normative tax theorist, who advocates such inclusion from reasoning based on equi-yield comparisons, responds to taxpayers by arguing that overall rates of tax may be lowered simultaneously with the widening of the base. But the taxpayers may be implicitly, but correctly, rejecting the equal yield postulate, in their predictions that any widening of the tax base must open up further taxing possibilities for a revenue-seeking government.

Illustrations might easily be drawn from American fiscal experience. For example, in late 1979, a proposal was widely discussed aimed at the introduction of a broad-based value-added tax with offsetting reductions in payroll taxes and individual and corporate income taxes. If such a proposal is adopted, it may be predicted that, ultimately, the value-added tax would be used to generate revenues greatly in excess of the revenue reductions under other taxes. In fact, of course, almost any widely advocated tax change tends to be justified in terms of its greater "efficiency," or its greater "fairness," springing from the extension of the tax base. As our analysis indicated, if our perception of postconstitutional political process bears any relation to reality at all, it is precisely on such grounds that the change should be rejected.

Appendix: Progression in the Multiperson Setting

The question of interest here is this: Can a progressive tax system raise more revenue than the revenue-maximizing proportional system, when there are many taxpayers? We have already shown that the revenue-maximizing proportional system always gives more revenue in the single-taxpayer case, or equivalently in the many-taxpayer case when all taxpayers are identical. Is this true more generally?

To investigate this question, we examine a simple two-person example, denoting the two individuals by A and B. We shall assume that B is "richer" than A—that Y_b exceeds Y_a at all tax rates. We further assume, for analytic convenience, that the individuals' demand curves for nonleisure activity have constant elasticities. We can therefore write

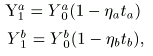(1)

where

Y₀ⁱ is i's pretax income
Y₁ⁱ is i's posttax income (expressed in dollars net of tax)
t_i is i's tax rate expressed as a rate on net income
h_i is i's elasticity of demand for "income,"

so that

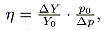and Dp = t, p₀ = 1, by assumption. The individually revenue-maximizing proportional rates, t_i*, can be derived by maximizing t_iY₁ⁱ in each case by simple calculus. On this basis, we obtain

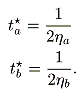(2)

The uniform proportional tax rate that maximizes revenue, t*, is obtained by maximizing the expression

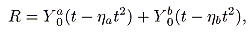(3)

which yields

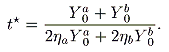(4)

From (4), it is clear that t* is a weighted average of sorts of t_a* and t_b* and must lie between t_a* and t_b*.

In fact, recalling that Y^b exceeds Y^a by assumption, a necessary condition for progression to yield more revenue than the revenue-maximizing proportional rate is that

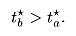(5)

If this is not so, a departure from t* by lowering the rate for earlier units of income or raising the rate on later units of income (to B) must reduce revenue. From this it follows directly, using (2), that

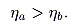(6)

To derive sufficient conditions, consider the revenue-maximizing "progressive" rate structure, which consists of two rates: t₁ over the range in which both pay tax and t₂ in the range where B only pays tax. Any additional progression must lose revenue. We can examine aggregate revenue in this case and determine the conditions that must hold for t₂ to exceed t₁. Accordingly, we examine

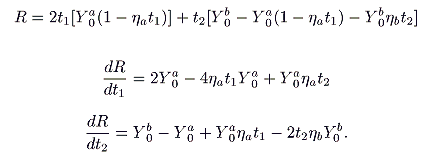(7) (8) (9)

Setting (8) and (9) at zero, we have the equation system

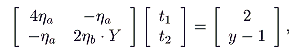(10)

where y = Y₀^b/Y₀^a (> 1). Thus, we have

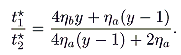(11)

For t₂* > t₁*, therefore, we require that

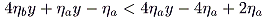or

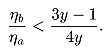(12)

Since 1 < y < ∞ (by construction), (12) requires that h_b/h_a be less than three-fourths, or that h_a be at least one-third larger than h_b.

We should note that if h_a is too large relative to h_b, then the revenue-maximizing arrangement in the proportional tax case may ignore A entirely and simply levy t_b*, and the progressive tax system becomes "proportional" anyway. That is, we require that t* < 1/h_a (since at t = 1/h_a, individual A ceases to pay tax entirely). In other words, we require that

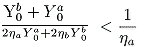or

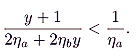(13)

That is,

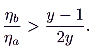Combining (12) and (13), we can specify the general requirement on h_b and h_a as

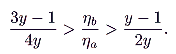(14)

For y in the neighborhood of unity, we require h_a to be more than twice as large as h_b. As y becomes very large, we require only that h_a be more than one-third larger than h_b—but not more than twice as large, since then the tax system will force A to earn no taxable income at all.

It is however clear that, for any value of y, there is a value of h_b/h_a that satisfies (14). Progression can therefore yield more revenue than proportionality, under the appropriate relative values of h_b and h_a.

Figure 3.4

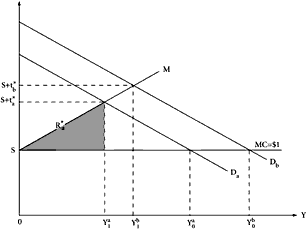
It is interesting at this point to contrast the results under the simple two-tier rate structure with those that emerge under a progressive tax system in which the marginal tax rate is a linear function of Y₁. Such a "linear" progressive tax is depicted in Figure 3.4 by the line SM. Now, under such a rate structure, the largest amount of revenue in the two-person case that could conceivably be obtained is exactly one-half of the maximum revenue obtainable under a regime in which the revenue-maximizing proportional rates, t_a* and t_b*, are imposed on A and B, respectively. This situation is depicted in Figure 3.4—the revenue obtained from B is at most ½R_b*, from A at most ½R_a*.

Let the revenue under this "linear progressive" rate structure be R_L. Then

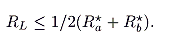(15)

Let the revenue derived from the revenue-maximizing uniform proportional rate structure be R_p. Then we know that B can be treated as if he were identical with A, so that R_p must be greater than or equal to 2R_a*; and A could be ignored entirely, so that R_p must be at least as great as R_b*. In other words,

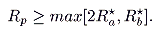(16)

Suppose that 2R_a* 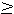R_b*. Then

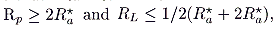so that

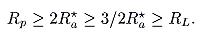(17)

If, on the other hand, R_b* 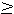2R_a*, then

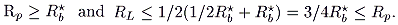In the two-person case, then, the linear progressive tax derives unambiguously smaller revenue than the revenue-maximizing uniform proportional system.

We can add a third party, C, where R_c* > R_b* > R_a* by construction. Then, by analogous reasoning,

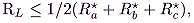and

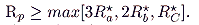Let 3R_a* 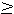2R_b* 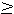R_c*. Then

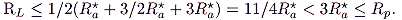And similarly, if R_c* 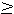3R_a*, 2R_b*, or 2R_b* 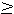3R_a*, R_c*. More generally, it can be shown by induction that

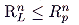(where R_Lⁿ is the linear progressive rate for n taxpayers). Assume that R_Lⁿ < R_pⁿ. Then

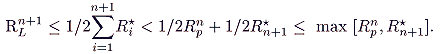Now, R_pⁿ⁺¹ must exceed R_pⁿ, since R_pⁿ is feasible (one could simply ignore individual n + 1). Moreover, R_pⁿ⁺¹ must exceed R_n+1*, since R_n+1* is feasible. Therefore,

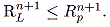So 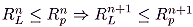; and since the result is true for n = 2, and n = 3 it is true for all n, by induction. Thus, the "linear progressive" schedule always derives less revenue than the revenue-maximizing proportional rate structure.

A third variety of progression is worth mentioning here. This is the degressive system mentioned in Chapter 3. Any such system, combining a flat exemption with a uniform proportional rate, must raise less revenue than the revenue-maximizing uniform proportional rate structure, since less revenue is obtained from each and every taxpayer.