The Power to Tax: Analytical Foundations of a Fiscal Constitution
By Geoffrey Brennan and James M. Buchanan
Publisher
none
- Foreword
- Ch. 1, Taxation in Constitutional Perspective
- Ch. 2, Natural Government
- Ch. 3, Constraints on Base and Rate Structure
- Ch. 4, The Taxation of Commodities
- Ch. 5, Taxation through Time
- Ch. 6, Money Creation and Taxation
- Ch. 7, The Disposition of Public Revenues
- Ch. 8, The Domain of Politics
- Ch. 9, Open Economy, Federalism, and Taxing Authority
- Ch. 10, Toward Authentic Tax Reform
- Epilogue
- Selected Bibliography
 Money Creation and Taxation
Money Creation and Taxation
There is no subtler, no surer means of overturning the existing basis of society than to debauch the currency.
—John Maynard Keynes,
The Economic Consequences
of the Peace, p. 236
Money creation can be and frequently has been used by government as a device for raising revenue. In this chapter, we wish to examine money creation as a revenue instrument, broadly conceived, from within our constitutional perspective, and with our characteristically monopolistic assumptions about the behavior of government. In some ways, this involves a simple extension of the analysis of the taxation of wealth undertaken in Chapter 5. We have, in particular, consistently noted the analogy between assigning some tax base,
X, to government and assigning to government a monopoly franchise in the provision of
X. At one level, we could simply reverse the analogy and assert that assigning to government a monopoly franchise in the creation of money is equivalent to permitting government to levy a tax on money holdings. Since money holdings are a subset of aggregate wealth, the relevance of our earlier discussion of wealth taxation is clear.
There is, however, enough that is unusual about money creation to justify a somewhat more detailed discussion. The analysis of money issue in the context of our basic perspective on politics turns out to be both intrinsically interesting and potentially significant in an empirical sense. The peculiarities of inflation as a revenue device will emerge in the ensuing discussion. There is, however, one aspect of money creation that sets it apart from anything we have discussed so far and which merits mention at the outset.
Previously when we have discussed the power to tax as analogous to a corresponding monopoly franchise, we have done so on the assumption that the sole function of the arrangement is to raise revenue. There has been no implication that in the absence of the exercise of the taxing power, the competitive market structure could not or would not provide the tax-base goods in a tolerably efficient and acceptable manner. There is no plausible argument that the supply and provision of goods that might be potential tax bases need be socialized. With money creation the case is not so clear. Monetary theorists engage in a long and continuing debate over whether competition in the supply of monetary instruments would be reasonably efficient or even whether competitive organization is at all feasible. The justification for the government’s possession of a monopoly franchise in the creation of money normally found in the literature is not based primarily on the implications for revenue raising: the revenue implications emerge as an incidental feature, to the extent that they are treated explicitly at all.
We do not ourselves wish to take sides in the debate over the possible efficacy of a free market in money. What we do wish to point out are the revenue implications of assigning to government a monopoly franchise in money creation, implications that emerge emphatically in our Leviathan model of politics. Our analysis concentrates on predictions as to how such a monopoly franchise will be exploited. Even if the market provision of money should be grossly inefficient in the standard economic sense, the costs of the predicted government alternative are relevant in any constitutional choice between possible institutional settings. And even if the market alternative should be rejected after careful institutional comparison, predictions about likely outcomes when government is assigned the power to create money remain crucial in setting the terms of the constitutional restrictions that the rational citizen-taxpayer might desire to impose on government in the exercise of that power.
Our argument in this chapter is organized in several stages. In Section 6.1, we develop some simple propositions about the revenue significance of the power to create money. In Section 6.2, we turn to the discussion of inflation specifically. We do so by appeal to an analogy between money and a durable physical asset, “land.” Our aim in this section is to point up the crucial role of expectations in determining the revenue significance of inflation and the monopoly money franchise. In Section 6.3 we consider the question of inflation and money creation more directly, using the analogy of Section 6.2. Section 6.4 attempts to indicate the sorts of expectations of government action that the citizen-taxpayer might be expected to hold. In Section 6.5, we contrast the tax on money balances with other forms of wealth taxation, and in Section 6.6, we attempt to indicate where our discussion diverges from the orthodoxy, and why. Section 6.7 offers some comments about the timing of revenue streams under alternative monetary constitutions. The relation between inflation and income-tax revenues is considered briefly in Section 6.8. We conclude in Section 6.9 with a broad methodological comment on the connection between existing literature on the “monetary constitution” and our own exercise of establishing an analytical basis for a “fiscal constitution.”
6.1. The Power to Create Money
Despite the widespread reference to inflation as a means of raising revenue, inflation is not the only aspect of government’s power to create money that has revenue significance. Even under a zero-inflation regime, the granting to government of a monopoly franchise in the creation of fiat money is worth something because this franchise carries with it the power to create at essentially zero cost an asset upon which individuals place economic value. In what follows, we offer a brief discussion of the nature of money in some very simple settings in order to establish elementary propositions about the revenue significance of the money-creation monopoly. This discussion also serves to set the analytic stage for the ensuing, and more detailed, discussion of inflation as a tax. Initially, however, we abstract from inflation entirely. We also abstract from the host of questions that have occupied the attention of monetary theorists relating to the issue of how money might emerge in a barter economy. We simply assume, for the purposes of our argument, that the government is to be assigned its monopoly franchise in money creation
ab initio. We shall restrict the analysis to an economy that is stationary; there is no growth and the basic parameters (wants, resources, technology) are assumed to be unchanging through time. The basic analysis could, of course, be readily extended to allow for economic growth and, hence, for increasing demands for money. For simplicity and economy in exposition, we shall forgo this extension here. As elsewhere in our book to this point, we assume the economy to be closed. In this setting, the government can, if authorized to create money, ignore any constraints that are imposed on its behavior by the presence of competing monies.
*72
We consider initially a simple two-period model. In period 1, a set of transactions among individuals occurs in which a set of buyers,
B, exchange cash for a set of goods initially in the possession of a group of sellers,
S. In period 2, these sellers,
S, must be able to exchange that cash for goods which they value, since the cash has no intrinsic value. If this were not so, the sellers would not accept cash for goods in period 1. The creation of money then requires that in the second period the money-creating authority must be in a position to replace cash with goods or their equivalent.
*73 If the money-creating authority is the government, how can this be done? There are two means:
1. The government can return to individuals the resources it acquired from them in return for cash at the beginning of period 1. Those individuals would have forgone interest on their money stocks in return for the transaction services of money. Government would have obtained an interest-free loan of an amount of assets equal to the money stock—which is worth
r ·
M, where
r is the rate of interest and
M is the real value of the money stock.
*74
2. The government can permit the cash to be “paid” in lieu of taxes. In this case, the government forgoes (part of) the real goods and services that it would otherwise have obtained in period 2, because it accepts cash in lieu of those real tax resources in that period.
It seems clear, from either perspective, that money is rather like a form of debt. Money creation permits the government to reallocate the fruits of its taxing power intertemporally: government can by virtue of its money-creation (and taxing) powers shift the period 2 tax revenues to period 1. In addition, however, because it needs to pay no interest on its implicit loan, government obtains from its power to create money the equivalent of the interest on the money stock. Government could invest the resources it obtains in return for cash in period 1, and “repay” an amount equal to the same absolute value of those resources in period 2, keeping the interest.
The power to create money therefore assigns to government the market value of the transactions services of money for revenue purposes. In this simple model, that power is contingent on the government’s preparedness to accept money as payment of tax liabilities, or equivalently on government’s preparedness not to use up the resource base that money creation initially provides. Here and throughout the subsequent discussion, we neglect the deposit banking: government fiat issue is the only money.
Let us now extend this model by removing the simplifying assumption of two periods. In the case with infinite time horizons, the value of the money stock to government is the present value of the infinite stream of transactions services it provides to citizens. In other words, the value to government of a perpetual interest-free debt is equal to the principal—the real value of the money stock itself, in this case. If government obtains
r ·
M per period forever, the capitalized value of this is 1/
r ·
rM, or
M.
It is quite clear therefore that, even in the absence of inflation, the power to create money is of revenue significance. The question we must ask here, however, relates to whether a Leviathan government could be expected to be content with the zero-inflation regime. What pattern of inflation (or deflation) might we predict Leviathan to choose? And what is the significance of this for the assignment of an unconstrained money-creation authority to government?
In order to answer these questions, we need to focus on inflation per se. In our discussion, we aim to do several things. First, we seek to establish the connection between inflation and the tax on money balances. Second, on the basis of this connection, we shall be able to reiterate the main conclusions of Chapter 5 concerning wealth taxes in specific application to inflation.
6.2. Inflation and the Taxation of Money Balances: A “Land” Analogy
To establish the connection between inflation and the taxation of money balances, and to illustrate the crucial role of expectations, we find it helpful to introduce an analogy. We shift attention to “land,” assumed here to be an infinitely durable resource.
*75 Suppose that government monopolizes the supply of this land, defined in normalized homogeneous units, but that the total supply is more than sufficient to meet the needs of the population. These conditions ensure that some units of land would remain unoccupied even if land were made freely available. The efficiency-generating price would, of course, be zero.
 |
| Figure 6.1 |
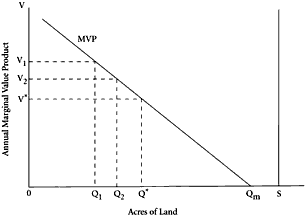
Consider, now, a sequence of periods. Suppose that, in period 1, the monopoly government decides to sell some amount of land, in a setting in which no land has been sold. There are two elements that will enter into the price which the market is prepared to pay for the quantity of land offered for sale: the rental value of that land given the quantity released; and individuals’ expectations about the level of land supply, and hence the market value of land, in future periods. Consider Figure 6.1. In this diagram, we depict the annual marginal value product per unit of land on the vertical axis, and the quantity of land measured in homogeneous physical units (acres) on the horizontal axis. The
MVP curve illustrates the way in which this annual marginal value product declines as the quantity of land in use increases. It indicates the price per acre that emerges in a market with free competition among buyers for an annual lease on the services of land, given the quantity of land released. For example, at quantity
Q1 the price of an annual lease of 1 acre of land is
V1. The aggregate supply of land is given by 0
S, and is by construction such that
MVP is zero at or before the quantity of land in use reaches 0
S.
 |
| Figure 6.2 |
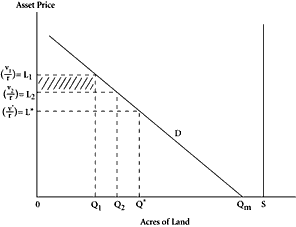
In our model, however, purchasers do not acquire annual leases but rather buy the right to permanent use. If the quantity of land
Q1 is released for sale in period 1 and if
Q1 is believed to be the quantity of land that will prevail indefinitely (i.e., if this is believed to be the only sale of land there will ever be), then the price per acre will be the capitalized value,
L1 (depicted in Figure 6.2), of the annual marginal value products; that is,
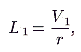 |
(1) |
where
r is the real rate of return on alternative assets. Suppose, however, that buyer expectations turn out to be wrong—that the government releases an additional (
Q2 –
Q1) units onto the market in period 2, making the aggregate supply
Q2 units. Suppose further that purchasers once again believe this release of land to be the last. Then the new price for land,
L2, will be the present value of the annual marginal value products obtained when
Q2 acres of land are in use; that is,
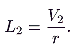 |
(2) |
The decline in land prices from
L1 to
L2 inflicts capital losses onto period 1 purchasers. In this setting, the release of additional units of land for sale acts as a wealth tax on all period 1 purchasers.
Given that all buyers expect the quantity in each period to be that which will prevail forever, we can show the price per unit of land in Figure 6.2 as
V/
r with
V determined from Figure 6.1. The curve
D shows how the price per acre of land changes as the quantity in use changes, and is the same as the
MVP curve with the vertical axis denominated in prices,
L, for a perpetual flow of annual rentals,
V, or
V/
r. In Figure 6.2, the loss to period 1 purchasers can be depicted as the shaded area (
L1 –
L2)
Q1: this is the additional revenue that government has obtained from being able to “fool” period 1 purchasers.
Of course, if the precise timing of the release of land for sale is known beforehand, each “generation” of buyers will pay for rights to ownership of land only the capitalized value of the future rental streams that the land makes possible. Hence, “generation 1” buyers would be prepared to pay for each unit of land a price,
P1, which is
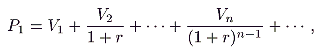 |
(3) |
where
V
i is the marginal value product of land in period
i and is a function of the aggregate supply of land,
Q
i, in use in period
i.
In this case, where the time pattern of release of land for sale is fully known by all purchasers, no capital losses will be sustained by any buyer: each buyer will earn a normal rate of return on land. Obversely, the government cannot obtain additional revenue from unanticipated land sales. In this case of perfect expectations, what would be the government’s (monopolist’s) revenue-maximizing strategy?
Since the time pattern of release is known, the revenue-maximizing arrangement is to maximize the rental value of the land stock in each period. This maximum is depicted in Figure 6.1 as
V*, prevailing when the supply of land is
Q*, and is derived from
MVP in exactly the same way as we derived the maximum revenue solution in the single-period cases analyzed in Chapters 3 and 4 (with the special consideration that here “marginal cost” is zero). Geometrically, with
MVP linear,
Q* is half
Q
m. This revenue maximum depends of course on our assumptions that the total quantity of land is more than sufficient to satiate all demands, and that the resource is infinitely durable. The government will release the entire revenue-maximizing supply,
Q*, all in the first period. To fail to release any part of that quantity in period 1 would involve an unnecessary sacrifice of revenue in that period.
This revenue-maximizing solution, analogous to the single-period case, depends crucially on the assumption that the future course of land release is completely and accurately predicted by purchasers. But precisely as with the capital tax discussed in Chapter 5, the purchasers of land in this example can only be secure in their predictions about government’s future release of land for sale if government undertakes a binding commitment that purchasers consider to be effectively constraining. If individuals do not really believe that any sale of land will be the final one as long as any land is held by government, they may not purchase land at any price. In this case, we are back in the dilemma-type situation discussed in Chapter 5; both individuals and Leviathan can be made better off by a mutually binding agreement. In the land example, a visible destruction of some part of the total supply might suffice.
Suppose, however, that individuals are not fully “rational” in this expectational sense and that they simply predict that the supply of land in each period will prevail indefinitely without any guarantee to that effect. What is the government’s revenue-maximizing strategy in this imperfect expectational setting? Here, government can obtain the full surplus to be derived from land. By adding an additional unit of land in each period, a set of prices for land will be traced out which follows
D in Figure 6.2 exactly—aggregate government revenue will be the area under
D.
*76
6.3. Inflation and the Taxation of Money Balances
Comparison of money and the land analogy. In some ways, money is similar to the land in our simple example, but in other ways it is profoundly different. It is similar in the sense that the time profile of supply determines the “price” in each period: all future releases onto the market will be taken into account in determining current prices. To the extent that individuals’ expectations about those future releases are in error, individuals will bear capital losses and government can increase its revenue acquisitions from sale above the “maximum revenue yield,”
L*
Q*. In much the same way, the demand for money depends on expectations about the future quantity of money that government may release. If those expectations are wrong, the government might obtain revenue significantly in excess of the maximum revenue yield when expectations about the future course of the money supply are completely accurate.
 |
| Figure 6.3 |
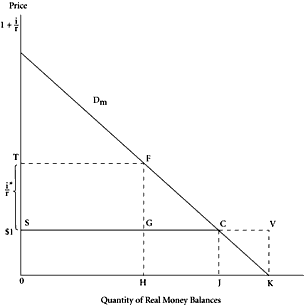
It will be useful to try to conceptualize the problem so as to make it as closely analogous as possible to the simpler land example introduced above. We can depict, in Figure 6.3, a “demand curve” for real money balances,
D
m. Care must be taken, however, in defining the units to be measured, along both the abscissa and the ordinate. Along the abscissa, we measure the quantity of real money balances, but it is useful to define these in units of initial period dollars,
M0. Along the ordinate, we want to measure the “prices,” or current capitalized costs, that individuals face in holding differing quantities of real balances, so measured, in perpetuity.
In this conceptualization, the demand curve for real money balances in Figure 6.3 becomes analogous to that for land in Figure 6.2. But there is an extremely important distinction between land and money that emerges here. As noted earlier, with land the supply or stock is measured in units of physical quantity directly (in acres, square miles, or square feet). The number of such physical units expected to be in productive use determines the prices that persons are prepared to pay for rights to permanent usage. The monopoly supplier can determine this price, or value, by changing the physical quantity offered for sale.
Money is dramatically different in this respect. It matters not at all whether money is denominated in dollars, dimes, or cents. The quantity of the nominal units of money, the parameter over which government may be allowed to exercise direct control, does not determine directly the value persons place on any given stock. The monopoly issuer of nominal money can determine the value that persons place on any given regime offering monetary services only by varying the rate of inflation—the rate of increase in the stock of nominal units. In a stationary or no-growth economy, the zero-inflation regime would yield to government an initial-period capital value, defined in units of initial-period money,
M0, precisely equal to the number of units created in that period. The price per unit placed on this money stock, and hence on the permanent “rights” to the quantity of real money balances indicated by the appropriate point along the demand curve, would be, quite simply,
$1. In this noninflationary regime, therefore, the capitalized value of the monopoly franchise to government is measured either by the area 0
JCS or by the distance 0
J in Figure 6.3.
In an inflationary regime, however, measurement of the capitalized value of a unit of real money balances becomes considerably more complex. In order to maintain a unit of real money balances in perpetuity, a person must reckon on suffering a current capitalized “cost” that is
larger than the number of initial-period dollars held in the form of monetary assets. Hence, the “price” for a unit of real money balances, defined in
M0, must exceed $1. Obversely, the value of the monopoly franchise to government must be larger per unit of real money balances under regimes with positive than with zero rates of inflation.
The “price” of a unit of real money balances, defined as a dollar’s worth of
M0, to be maintained in perpetuity may be computed more precisely as follows:
1. The current or initial-period portion of the “price,” which is simply the initial-period $1 held in the form of monetary assets; plus
2. The present value of the increments to the initial allocation of resources to money balances that will be required in order to maintain the same real (and desired) stock of real balances. (Since no increments need be added in the noninflationary regime, this second term becomes zero; hence, as noted above, the capital value of a dollar’s worth of real balances in perpetuity is $1.)
In a regime with a preannounced and permanent positive inflation rate,
i, invariant as among periods, there must be an increment in resource requirements in each period. To get a current capitalized value, these increments must, of course, be appropriately discounted. The aggregate cost of these increments in present-value terms is given by
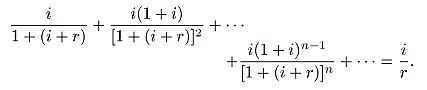 |
(4) |
Hence, the “price” for a dollar’s worth of real money balances, in
M0 dollars, is
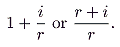 |
The revenue-maximizing government will select that rate,
i*, which given the demand for money,
D
m, will maximize
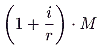 |
(5) |
because money is costless to produce.
*77 This maximum is obtained when
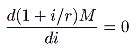 |
(6) |
or when
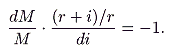 |
(7) |
a familiar condition requiring that the price elasticity of the
D
m curve in Figure 6.3 be unity. Note that this problem is again almost equivalent to that confronting the land monopolist discussed above. The one difference is that the value placed on any stock of real money balances can only be altered by changing
i, rather than some independently measurable physical quantity.
With linear demand curves, the revenue-maximizing solution will be determined at that quantity of real money balances where marginal revenue equals marginal cost (in this case, zero), indicated by
H in Figure 6.3. Note that the quantity of real money balances in this solution will always be precisely
one-half that quantity which would be dictated by an “optimum” regime, where the negative rate of inflation must offset the positive real rate of interest.
*78
Quite apart from considerations relating to revenue-maximizing government, the formulation here is helpful in any assessment of the genuine opportunity costs of any regime of permanent and continuing inflation. By utilizing the formula
M0 (1 +
i/
r), and by selecting values for
i and for
r, we can define the capitalized costs for a unit of real money balances under differing regimes. Consider, for example, an
i of 10 percent, with an
r of 2 percent, chosen as plausibly descriptive for the United States in 1980. In this case, the capitalized cost of a dollar’s worth of real balances, defined in the
M0numéraire, is $6. This says, quite simply but dramatically, that the cost of maintaining a unit of resource value in the form of monetary assets in a continuing regime described by these parameters is
six times the cost of maintaining a unit in a noninflationary regime. Even if the positive rate of inflation only matches the real rate of interest, the cost of maintaining real money balances doubles over that incurred in the zero-inflationary setting.
The foregoing analysis is applicable only to those settings where the government is presumed able to select one from among a set of alternative permanent inflationary regimes with rates of inflation stable through time, a selection that both individuals and the government treat as binding. In our land example, we noted that the government monopolist could guarantee against further exploitation by destroying a part of the total stock. Even in the absence of this sort of demonstrated protection, however, additional releases of land for sale, beyond the revenue-maximizing quantity offered in the initial period, would drive the incremental gains to government toward zero. Money is also quite different from land in this respect. Government can add to the nominal stock of money without limit and without necessarily driving the value of additional increments to zero. For example, if the population systematically believes that each current addition to the money stock is the last that will ever be made, the real revenue that the government can obtain approaches 0
JCS (Figure 6.3)
in each period. By an appropriately large increase in the number of units of nominal money, the government can reduce the value of all previously existent units to insignificance. On each occasion all individuals believe the increase in the money stock to be a once-and-for-all denumeration of the currency; but such a “once-and-for-all” denumeration occurs each period. Of course, no such set of expectations is in the least plausible, but the point remains that with an analogous set of expectations the same outcome could not emerge in the land case.
The crucial question in all this is clearly the delineation of a set of expectations that is plausible. What would it be reasonable for the taxpayer-money holder to believe about government monetary strategy? What expectations are “rational” in this setting? The answer clearly depends on the maximand which the taxpayer-money holder attributes to government, and the severity of the constraints (electoral and otherwise) which he believes to apply—that is, on the particular “public-choice” model which implicitly informs taxpayer-money holder-citizen actions. In keeping with our discussion elsewhere in this book, we wish to explore the implications of one particular model of “public choice”—the Leviathan model—which we believe to have considerable relevance, both potential and actual, to the real political world.
6.4. Inflationary Expectations under Leviathan
In order to explore more fully the question of what expectations concerning inflation individuals might rationally adopt under Leviathan government,
*79 we shall examine three simple cases:
1. A three-period model, with permanent Leviathan.
2. An infinite-time-horizon model, with permanent Leviathan.
3. An infinite-time-horizon model, with probabilistic Leviathan.
In each case, the assumption is made that fiat money is acceptable by the government in payment of taxes so that the implicit resource base of the money stock is validated. We also assume that other taxes exist of such magnitude as to ensure that liabilities more than absorb the payback requirements of fiat money issue.
Permanent Leviathan: the three-period case. Suppose in period 1 that the government releases an initial money stock of 100 units and that taxpayers believe that no increase in the supply of money will occur in the second period. They will then exchange for that money stock a certain quantity of real goods and services—$100’s worth at period 1 prices. When period 2 comes, the revenue-maximizing government has a clear incentive to inflate to the maximal extent possible. If, for example, it increases the money stock to 1000 units, and individuals believe that no further inflation will occur, there will simply be a denumeration of the currency so that new prices are 10 times the old ones. By this period 2 inflation, the government obtains a further quantity of real goods and services equal to nine-tenths of the quantity that it obtained initially. In the third period (and final period in this model), the government simply allows individuals to use cash to pay off their tax liabilities at second-period prices—a real payment of $100’s worth at period 1 prices, or $1000’s worth in period 2 prices. The government has gained
additional revenue here equal to nine-tenths of the value of the money stock (when inflation is expected to be zero). What has happened is that the initial “loan” of real resources made by individuals to government when they accepted money (interest-free debt) is effectively denumerated in money terms. Those individuals can in period 3 only “buy back” tax relief at
period 3 prices. Inflation enables government to organize for itself a capital gain worth virtually the full amount of the real value of initial money stock. We should note that this incentive toward maximum inflation is independent of individuals’ inflationary expectations. If citizens believe that a tenfold increase in the money stock will occur, they will be prepared to hold money only up to the point where the capital losses due to the inflation are compensated by the transactions virtues of money. Period 1 prices (i.e., the relative values of goods and money) will be such as to be equal to period 2 prices minus the marginal benefits of holding money per se. Whatever initial price level obtains, however, it is always in Leviathan’s interests to inflate to the maximum possible extent.
Recognizing that maximum inflation—independent of inflationary expectations and hence of initial prices—is the dominant strategy for Leviathan,
the rational citizen will not hold any cash balances at all. The taxpayer-government interrelation is precisely identical to that which occurs with a tax on wealth,
*80 and can be depicted in the game matrix as shown in Table 6.1. The taxpayer will recognize that if he holds cash, the government will maximize the rate of inflation, hence imposing a cost larger than that consequent upon holding no cash balances at all. The predicted outcome is the lower row, with zero payoffs to both parties, whereas both could secure positive payoffs in the upper right-hand cell.
| Table 6.1 | ||
|
|
||
| Government
|
||
| Taxpayer | (1) Maximum inflation |
(2) Restraint |
|
|
||
| (1) Hold cash | [- a, + c] |
[+ a, + b] c > b |
| (2) Zero money balances | [0,0] | [0,0] |
|
|
||
Permanent Leviathan: unbounded time horizons. Games of the sort depicted above are, as is well known, more likely to have socially superior solutions when played over long periods, particularly if there is no end point. Even in the absence of an explicit monetary constitution, government may rationally refrain from inflicting maximum inflation in every period in the expectation that individuals may be induced to hold positive cash balances. Since a necessary condition for holding positive cash balances is that citizens believe that government will not maximally inflate, it is in government’s interest to establish an environment in which citizens hold those beliefs. To do this, Leviathan needs to play a strategy of restraint.
It is, however, clear that any outcome of this type, in which individuals hold positive cash balances and Leviathan exercises voluntary restraint in new money creation, is inherently precarious. If such an “equilibrium” can be achieved, it seems reasonable to suggest that it may also be achievable
after implicit agreement has broken down. In that case, the cost to Leviathan of departing from the “equilibrium” is determined by the number of periods (noninfinite) in which individuals will aim to hold zero money balances, until confidence in government restraint is reestablished. Periodic departure from the policy of restraint may therefore be in Leviathan’s interests.
*81
A very simple form of the playing of such a game is described in a short note by Harry Johnson.
*82 In Johnson’s discussion, he assumes (Cournot-like) that citizens believe that government will in each period inflate at the rate applying in the previous period. In this rather simplistic case, he shows that it is rational for Leviathan to depart from a stable inflationary equilibrium and “play” alternately high and low rates of inflation. In other words, the constant rate of inflation strategy is dominated by the policy of alternate high inflation and low inflation.
As Johnson himself observes, the expectations imputed to citizens in this model seem highly questionable. But it is of the essence that, in situations of this type, expectations are difficult to model. A small increase in inflation rates may lead individual money holders to unload cash very quickly, if it leads citizens to believe that larger inflation rates are imminent. Alternatively, quite substantial variations in the money stock may lead to little change in real money balances or inflation rates. The adjustment of desired real money balances (and therefore prices) to changes in the money stock seem impossible to predict here, but seem likely to be extremely volatile. Needless to say, in this setting, the “revenue-maximizing inflation rate” as derived in a world of perfect foresight is totally inapplicable—and indeed must be under anything other than a fixed predetermined monetary rule, because it is only with such a rule that perfect foresight is possible. In much the same way, the extent of revenue that may be obtained from the money-creation power must remain somewhat doubtful. The level of money balances individuals would be prepared to hold in the absence of a given money rule is presumably quite different from that which they would hold in the world of perfect foresight. Whatever the influence on revenue potential, it seems clear that the welfare costs in terms of surplus forgone will be much higher in the absence of a fixed money rule. As we have shown in Chapter 5 in relation to wealth taxes more generally, if governments have discretion over effective rates welfare losses seem certain to be higher than in the case where tax rates are known with certainty
ex ante.
Probabilistic Leviathan. In what ways would the foregoing model be altered if governments only assume Leviathan attributes occasionally? One of the interesting features of the perpetual Leviathan model is that it seems likely that government would
not be motivated to act so as to maximize aggregate revenue in each period. Leviathan-like attributes will not always be in evidence. This is because the cost in revenue forgone in future periods exceeds the benefit in current revenue obtained—at least over some range.
With a Leviathan government operative in fact only occasionally, these prospects of lost revenue in future periods are hardly relevant. These costs will not be borne by the revenue-maximizing government itself. Hence, when and if such a revenue-maximizing government does come into power, it could be expected to inflate to the maximum extent possible. As long as notes have value, it will continue to print them.
In one sense, this model introduces an additional element of volatility into taxpayer-citizen expectations. If a government is recognized to have Leviathan-like properties, a very rapid inflation may ensue as individuals try to dump cash on the market—and this sort of inflation could be substantially independent of any increase in the money stock as such. The modest built-in constraints in the perpetual Leviathan model are not operative in this situation, and taxpayers-citizens will recognize this fact. Even the risk of massive exploitation through inflation will not necessarily be sufficient to prevent individuals from holding any cash at all. But such risk will rationally be taken into account in determining the desired quantities of real money balances. It is interesting to note here that the taxpayer-citizen may gain virtually nothing from the relative frequency of “good” government. If government has the power to create money, the citizen who holds cash remains open to exploitation by the occasional revenue-maximizing Leviathan who may obtain office, and the costs of potential exploitation may not be much different from those that would be incurred under a continuous revenue-maximizing Leviathan.
6.5. Inflation, Wealth Taxation, and the Durability of Money
Since we have, in the foregoing analysis, provided what is essentially an application of our earlier discussion of wealth taxation, it may be useful here to indicate one sense in which the taxation of money balances differs from the taxation of most other assets. Suppose, for example, that at time
t1 government announces a future increase in the money stock, say at time
t3, of some magnitude, say
x percent. In what way would this be different from a tax on whiskey stocks, or some other physical asset, at an equivalent rate, with identical advance warning? The answer is that it would be different in that, whereas whiskey can be drunk, and physical capital can depreciate, money has no intrinsic value and does not physically decay. The only possible response to the anticipated inflation for the money holder is to trade money for other things. The original nominal money stock remains, and prices adjust totally to allow for its anticipated depreciated value. The extent of the advanced warning of the increase in the money stock is therefore immaterial in a way that it is not in the case of most other capital assets.
In the standard literature, this absence of adjustment prospects is a desirable feature of a tax. Real money balances will adjust subsequent to the announcement of the future inflation; but, since someone in the community must continue to hold all of the nominal money units in existence, there is no net “escape” or “evasion” from the burden of the inflation tax. In this highly restricted sense, the welfare loss is minimal. But precisely because of this feature, note that the money-creation power may offer greater scope for fiscal exploitation of the taxpayer than that offered by the standard form of wealth tax.
6.6. The Orthodox Discussion of Inflation as a Tax
It may be useful at this point to contrast our own discussion of inflation as a tax with the prevailing orthodoxy—that essentially follows the approach taken in Martin Bailey’s influential 1956 article.
*83 A brief review of that paper seems appropriate here. The central element in the Bailey discussion is a diagram similar to that of our Figure 6.3. However, whereas our construction embodies capitalized values for permanently available units of real money balances, Bailey’s basic diagram is constructed in a single-period or time-rate dimension. Bailey’s objective is to measure the welfare cost of inflation in a manner “which is fully analogous to the welfare cost or ‘excess burden’ of an excise tax on a commodity.”
*84 He does this by considering an increase in the rate of inflation from zero to
i*, so as to produce a shift from
S to
T in Figure 6.3 where individuals expect the inflation rate
i* to prevail over the indefinite future. Bailey measures the resultant welfare loss as area
FGC, and by appeal to certain of Cagan’s results on European hyperinflations, he attempts to indicate the magnitude of the welfare loss per dollar of revenue raised from inflation at various levels. He also attempts to identify plausible maximum revenue rates of inflation for certain countries.
Subsequent criticism has succeeded in refining the Bailey analysis. As Tower
*85 points out, Bailey implicitly assumes that a zero-inflation regime is optimal, and he calculates welfare losses by reference to the zero-inflation “price,”
r in his model, $1 in our construction. For example, Bailey measures the welfare loss involved in the move from an inflation rate of zero to
i* as
FCG, rather than
FHK, the correct measure. This zero-inflation base has implications also for Bailey’s calculations of revenue-maximizing inflation rates. He derives the revenue-maximizing inflation rate as that rate which maximizes the revenue increment over and above the zero-inflation rate, rather than that rate which maximizes the total present value of the money-creation power.
*86
So much for a sketch of the prevailing theory of inflation as a tax. Our differences with this orthodoxy should be obvious. As we have been at pains to point out in the previous discussion, there is a fundamental distinction between the world in which a fixed monetary constitution (a money rule, perhaps) prevails, and the world in which there is no such constraint on government’s monetary behavior.
Given plausible assumptions about the behavior (or possible behavior) of government, it is only in the former world that the rational citizen’s monetary expectations are stable. When government has discretion to determine the money supply, the citizen’s expectations must be highly volatile. Any slight departure from the status quo may with equal plausibility be interpreted either as a minor anomaly or as evidence that major recourse to the printing press for revenue purposes is in the offing. The rational citizen’s response is, however, quite different according to which interpretation he adopts. The basic point is that, in the absence of a genuinely binding monetary constitution, any monetary equilibrium must be inherently precarious.
If the relevance and importance of this expectational difficulty is accepted, several conclusions follow. First, the Bailey model, essentially translated into our own construction in Figure 6.3, is only applicable in the strict sense to a world in which a binding monetary constitution is operative. The model can be used to determine the welfare implications of one monetary rule rather than another: one for example that involves a predicted inflation rate of
i0 rather than
i*. But it cannot be used to examine the welfare implications of an increase in inflation rates in-period, because such an increase is only possible when a binding monetary constitution is not in being. In the same way, the Bailey model, like our own, can be used to define that monetary rule from among the set of all possible rules that would maximize to government the present discounted value of the real money stock. Such a calculus might be relevant if government were required to select a binding rule and stick to it. But the basic Bailey model cannot be used to specify the revenue-maximizing monetary strategy of a government when no such money rule prevails, where no such precommitment need be made. One of the interesting anomalies of the Bailey analysis is the fact that in European hyperinflations to which he draws attention, actual rates of inflation were in many cases grossly in excess of those which seemed revenue maximizing in terms of the parameters of his model. Why governments might choose to inflate beyond revenue-maximizing limits becomes the obvious question. Were government decision makers malevolent, stupid, or irrational? One obvious answer is that they need have been none of these. They may, in fact, have been aiming to maximize revenue. Bailey’s calculations of revenue-maximizing strategy may have been inappropriate to the setting in which those governments were operating. The derivation of a revenue-maximizing monetary
rule is irrelevant to the understanding of revenue-maximizing monetary
strategy when no binding rule prevails. More generally, the “monetary-rule” analytics are, and can be, only marginally relevant to explaining what we observe in a world where no such rule prevails—and this particularly in relation to hyperinflationary situations. Equally, these “monetary-rule” analytics are of little use in deriving the welfare costs of inflationary finance in a setting where the monetary authority is not effectively constrained.
It can be seen therefore that our discussion and the orthodox inflation-as-a-tax discussion are addressed to different issues. We have been concerned to specify the implications of assigning to government constitutional authority to create money in the same way we have discussed the implications of assigning government the power to raise revenue from other sources, in Chapters 3 through 5. We have specifically examined this issue in a setting in which government has discretion to determine the use of its assigned money-creation power. The orthodox inflation-as-a-tax discussion, however, implicitly assumes that such discretion is precluded by some additional constitutional constraint that imposes a money rule, and seeks to derive the welfare implications of alternative money rules in this setting. Insofar as credibly binding money rules are not in practice operative, this orthodox discussion is dubious as a guide either to positive explanation of what we observe or to normative policy conclusions.
6.7. The Monetary Constitution
The Leviathan exploitation of the revenue potential of the money-creation power is a possibility that will be among those to be reckoned with in the constitutional deliberations of the citizen when he considers the possible efficacy of granting independent powers of money creation to government. As the analysis is intended to suggest, it is difficult, if not impossible, to construct an argument that could offer coherent logical support for such a delegation of power in any open-ended sense. Equally, the analysis suggests that
constitutional rules for money creation may be among the alternatives considered in any efficient set of fiscal-monetary arrangements. If, on the one hand, conventional tax instruments are chosen that will generate an approximately efficient level of public-goods supply when exploited to their maximum revenue potential, the citizen will wish to guard against additional revenue raising through money creation. Government franchise in money creation may be constitutionally prohibited. Alternatively, the individual may deny government access to standard tax arrangements sufficient to finance desired public expenditure levels and instead allow government access to the inflationary financing option. Whereas with most taxes the assignment of the
base is sufficient, however, it seems likely here that rate limitations will also be desirable, probably even to Leviathan itself. In this sense, the monetary constitution, embodying some set of rules relating to the extent of monetary expansion, is necessarily more restrictive than the fiscal limitations we have been discussing heretofore—both base
and (maximum) rate limits are involved.
A constitutionally selected and enforced rate of inflation that would provide government with funds sufficient to finance an estimated desired quantity of public goods would not run into the confidence dilemma previously discussed. But this difference emerges precisely because the rate of inflation is chosen constitutionally, as a rule to be enforced on government, rather than an announcement of intent by government. In this context of a constitutionally selected institution for financing governmental outlays, inflation does become a simple tax on money balances, and, as such, it might be considered along with other taxes on capital stocks, which would also have to be designed to embody constitutionally designated rates to prove at all acceptable.
Our purpose in this book is not to discuss properties of an optimal or desired monetary constitution, which may or may not include a constitutionally designated rate of inflation as a viable alternative for consideration. Our more limited purpose here has been to consider, even if briefly, inflation as a tax and to determine the prospects of reconciling this sort of fiscal instrument with the choice calculus of the citizen who models government in Leviathan terms.
However, in the light of our earlier discussion of wealth taxes more generally, there is one aspect of the “monetary constitution” that Bailey’s analysis and indeed all the relevant literature seems to have overlooked and that is important in the setting outlined here. Bailey’s analysis and the subsequent literature focus solely on the welfare losses attributable to different rates of inflation. But it is clear that inflation—of the steady, totally preannounced, and legally binding type—not only distorts asset choices and not only determines the magnitude of government revenues; it also determines the timing of the revenue stream which the money-creation power makes possible.
For example, assuming a stationary economy, a zero-inflation monetary constitution implies that the full revenue value of the money-creation power under this constraint, 0
JCS in Figure 6.3, accrues in the initial period when the money supply is introduced. By contrast, the less constrained monetary constitution embodying a positive fixed inflation rate of
i* increases the total present value of the money-creating power to the capitalized value 0
HFT in Figure 6.3. But only a portion of this present value can be secured by government in period 1. The additional value accrues in equal annual increments, as inflation proceeds, and the present value of those increments in real terms is the area
SGFT. Analogously, the “optimal” rate of inflation in the Friedman analysis involves an initial value of the money stock of 0
SVK but annual interest payments which in present-value terms are exactly equal to that initial value.
If the money-creation power is to be used for financing desired public goods and services under a Leviathan government or the possibility of one, this timing pattern is clearly of some account in its own right. To provide the desired time stream of public goods, one presumably requires continuous spending. Under a continuous benevolent government, we might conceive of a situation in which the “sale” of money in the initial period serves to establish a sinking fund, the interest from which is used to finance ongoing spending. Once one allows the possibility of revenue-maximizing Leviathan, however, this possibility seems unlikely to be feasible: any sinking fund would surely not survive beyond the period in which Leviathan is in office. Since inflation involves spreading revenue over time, the problem of lumpiness in the time stream of revenues becomes less severe under a monetary rule with a positive inflation rate. For example, as the constitutionally specified rate of inflation rises from zero to
i* in Figure 6.3, the initial real value of the money stock in period 1 falls from 0
SCJ to 0
HGS, but the present value of the revenue attributable to future inflation rises from zero to
SGFT. To equalize the revenue stream in every period would require an inflation rate of 100 percent: the proportionate increase in the nominal money stock in every period would be the same.
Consequently, the timing characteristics of the revenue flows become more desirable as the constitutionally appointed rate of inflation increases, over the range up to 100 percent. On the other hand, welfare losses increase and beyond some point the aggregate revenue may decline as the rate of inflation embodied in the monetary rule rises. Some trade-off here is presumably required. What seems clear is that the Friedman “optimal” money rule may not be optimal, even in the restricted limits of the model used, once these timing problems are confronted. Negative or zero inflation rates may not be preferred: moderately high rates of inflation may be.
One implication here is that there is no way that the power to create money can be divested of its revenue implications by a money rule alone. This may be viewed as a persuasive argument for relying on possibly imperfect market alternatives, and denying government the power to create money under any circumstances at all.
6.8. Inflation and Income Tax Revenue
Throughout this chapter, we have focused on the direct effects of money creation as a revenue device in its own right. We have ignored the possible indirect effects of inflation on revenue arising from its intersection with income taxation, a topic that is probably more familiar to mainstream public-finance specialists than those we have dealt with here. These indirect effects are of two types. The first and most obvious is that inflation, in the absence of any countervailing measures, increases real rates of progressive income taxation by pushing taxpayers into higher tax brackets.
To the extent that these apparently gratuitous effects of inflation are less conspicuous than explicit tax-rate increases, it follows that inflation presents government with a discreet and unobtrusive means of raising additional revenue. Such a possibility hardly fits neatly into our analytic framework. We have not introduced “fiscal illusion” at any other point: the entire discussion so far has proceeded in the bright glare of full taxpayer rationality. Leviathan is unashamedly exploitative, and taxpayers are completely aware of this. The revenue-maximizing rates for a given degree of progression will be arrived at, and beyond some point at least, increases in those rates can only reduce revenue. Discussion of this problem properly belongs to an analysis of fiscal illusion, and we have not included any such analysis in this book for obvious reasons of economy.
*87
The second aspect of the interaction between inflation and income taxation does not depend on progression at all, but rather on the extent to which income taxation, by virtue of taxing property income as well as labor income, involves an element of wealth taxation. As mentioned in Chapter 5, the extent of this tax on wealth can be increased by increasing the rate of inflation, given that nominal property returns are taxed. For example, if the rate of inflation is 9 percent and the real rate of return 3 percent, a nominal income tax rate of 25 percent becomes equivalent to an effective rate of 100 percent on property income. By setting the rate of inflation at the required level, it becomes possible for a single income tax to obtain maximum revenue both from labor income and from wealth without any overt discrimination, even though the demand elasticities between leisure and effort on the one hand, and between present and future consumption on the other, are quite different. This possibility would not of course be present if the “income tax” were levied solely on consumption expenditure.
6.9. Monetary Rules and Tax Rules
Two separate features emerge in a consideration of monetary rules that warrant more discussion, even if that discussion is brief. The first involves the notion of “efficiency” or “optimality” in monetary rules; the second involves the underlying presuppositions about the workings of government. These features combine to suggest that, at least in some respects, the monetary-rule discussion provides a plausible lead-in or bridge to our basic model of analysis.
As the analysis of this chapter has indicated, the welfare economics of “inflation as a tax” almost necessarily draws attention to the
rate of inflation through a sequence of periods. It would be analytically meaningless to refer to an “optimal” rate of inflation in a strict one-period model. “Optimality” or “efficiency” in the monetary context, therefore, must refer to a policy that embodies some multiperiod dimension.
In present-value computations, such as those embodied in the construction of Figure 6.2, the multiperiod dimensionality of the model necessarily emerges. One of the reasons for the ambiguities in the application of the Bailey-type analysis may stem from the single-period or flow model, which may have obscured the fact that the model’s relevance is limited to alternative permanent regimes. The multiperiod setting is in sharp contrast to the single-period setting assumed for most of the equi-revenue models for determining “optimality” in the allocation of tax shares. In a real sense, the discussion of monetary rules must be quasi-
constitutional simply because a “rule” by its nature must remain operative over an indefinite future.
The definition of the optimal monetary rule or the optimal rate of inflation that has emerged from the welfare analysis of inflation as a tax is, however, somewhat bizarre when looked at in comparison with familiar tax norms. As enunciated most clearly by Friedman, and, as noted above, in the standard model, the “optimal” rate of inflation is the negative offset of the positive real rate of interest. If the real rate of interest in the economy is 2 percent, the “optimal” monetary rule involves deflation at 2 percent per period. The logical basis for such an attribution of optimality lies in the zero (or near-zero) cost of creating nominal money. To prevent persons from economizing uneconomically on the use of money, it is necessary that money be made available at its genuine marginal cost, defined in opportunity-cost terms as the risk-free rate of yield on assets in the economy. Only if money itself is made to yield a positive return will such efficiency in individual portfolio adjustment be ensured. To implement such a monetary rule, however, government will necessarily be required to generate budgetary surpluses sufficient to allow for the reduction in the money stock period by period.
In this setting, there is no excess burden, no efficiency loss, from the monetary sector. The full value of the “money-users’ surplus,” the value of money for transactions purposes, is captured by the users themselves. No part of this value is captured by
government: government is not allowed to secure any of the rent that is implicit in possession of money-creating power.
This notion of “optimality” seems straightforward enough until it is placed alongside the standard tax analysis. In commodity taxation, for example, an equivalent “theorem” could readily be derived, and proved, to the effect that the “optimal” rate of tax for any commodity is
zero. In such a case, no excess burden is generated; efficiency losses are zero; and the full rent of commodity production, under competitive conditions, accrues to consumers. And since the result can apply to any commodity taken in isolation, it must also apply to every commodity and, indeed, to any and all conceivable bases of tax. But it would mean very little to say that optimality in taxation involves zero rates on all potential bases.
*88
Since, by presumption of the whole analysis, government must collect some revenues, we are necessarily in a regime where some excess burden must be anticipated. Once this situation is recognized, the implicit tax on money balances that any departure from the so-called optimal monetary rule introduces is to be compared with taxes on other possible bases, and some overall optimality in taxation may then be defined. All of this follows directly from within the frame of orthodox tax analysis; this critique does not in any way depend on either our constitutional or our Leviathan perspective.
From the latter perspective, the rational selection of some monetary rule is not determinate a priori, at least not independently of the effects of taxing alternative bases and of the demands for governmentally provided services. The optimal tax on money balances cannot be determined in isolation any more than could an optimal tax on beer.
A second feature of the monetary-rule discussion concerns the implicit assumptions made about the workings of the political process. Many economists have lived with the contradiction that government can, in some way, be “trusted” to allocate tax shares benevolently in accordance with criteria for efficiency and equity, but that the same government cannot be comparably trusted to keep monetary creation within desired limits. These economists have tended to support monetary rules, as if these are to be constitutionally enforced, while they neglect tax rules and may even oppose any introduction of such constraints.
*89 The anomaly here may stem from the observed rates of inflation, which seem to be out of line with any model of “responsible benevolence” on the part of government and its arms and agencies. By contrast, increases in the levels of taxation beyond desired limits are less readily observable, and these intrude less directly on the consciousness of citizens.
Nonetheless, the familiar tendency to model government behavior nonbenevolently with respect to monetary policy actions does seem to offer a plausible bridge to an acceptance of the generalization of such a model offered in this book, and specifically the extension to tax actions by government. To the extent that the rules side in the “rules versus discretionary authority” debate in monetary policy circles wins adherents, the prospects for serious examination of “constitutional tax rules” in lieu of “discretionary tax policy” surely must improve.
The Denationalization of Money: An Analysis of the Theory and Practice of Concurrent Currencies (London: Institute of Economic Affairs, 1976).
Money, Wealth and Economic Theory (London: Macmillan, 1967).
rM. There are some interesting aspects to a regime of annual monies, not the least of which is that it seems to deprive government of any possible benefits from inflation. However, money as we know it is a durable asset—a stock, not an annual flow of transactions services—and all our discussion here is predicated on that fact.
Q* compensates government for the interest it forgoes in postponing the receipt of revenue from the sale of extra units. For example, in period 1, Leviathan could either release
Q1 units at price
L1, aiming to release an extra (
Q2–
Q1) units next period, or could release all
Q2 units at price
L2. In the former case, it obtains
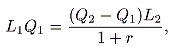
Q2–
Q1) units. In the latter case it obtains
L1 –
L2 > r (
L2Q2 –
L1Q1).
L*, the right-hand side of (3′) is positive and may exceed the left-hand side. If so, Leviathan will move instantly to (
L*,
Q*) and proceed to add successive units beyond
Q*. In this range, the right-hand side of (3′) is negative, so that (3′) always holds.
i, if the real money stock held each period is
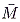 ? Now
? Now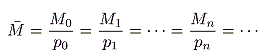
numéraire. The real revenue that government obtains in each period is
rM by virtue of interest on
M that it does not have to pay, plus
iM by virtue of deflating the real liability that money represents. This revenue stream is in terms of some real
numéraire and must be capitalized by the real rate of return to yield to
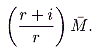
The Optimum Quantity of Money and Other Essays (Chicago: Aldine-Atherton, 1969), pp. 1-50.
Journal of Monetary Economics, 2 (April 1976), 169-83; and R. E. Lucas, “Econometric Testing of the Natural Rate Hypothesis,” in O. Eckstein, ed.,
The Econometrics of Price Determination Conference (Washington, D.C.: Board of Governors of the Federal Reserve System, 1972). Like economic orthodoxy generally, these models do not contain a specific objective function for government, although implicitly, government is considered to be interested in promoting the standard macroeconomic policy goals. The models concentrate attention on the prospect that the individual will be able to act on the same information that is available to government; hence, government cannot independently influence behavior in a way that is not subsequently validated. Government cannot “fool the people.” Our revenue-maximizing Leviathan does have a specific maximand, and the fully “rational” citizen-taxpayer may know what this is, but such knowledge cannot eliminate the strategic aspects of the interaction between the individual and government, as our analysis indicates. For example, if the individual predicts that Leviathan will adopt the revenue-maximizing permanent rate of inflation and acts on this prediction, Leviathan will find it to its own interest to inflate beyond such limits. To our knowledge, the only specific critique of the rational-expectations literature that concentrates on these strategic aspects is that by Gerald P. O’Driscoll and Andrew Schotter, who do not, however, model government in Leviathan terms. See Andrew Schotter and Gerald O’Driscoll, “Why Rational Expectations May Be Impossible: An Application of Newcomb’s Paradox,” Discussion Paper, Center for Applied Economics, New York University, November 1978.
Inflation in the World Economy, ed. Michael Parkin and George Zis (Manchester, England: Manchester University Press, 1976), pp. 73-86.We should note that a shift from a high rate to a low rate of inflation may, for a short period, increase rather than decrease government’s revenue-raising potential in money creation. If the shift causes persons to expect higher values of the money unit, they will seek to increase money balances. Government may, temporarily, gain more from the increased money creation dictated by a response to this demand than it loses by the initial shutdown or slowdown of the presses. On this point, see Gordon Tullock, “Can You Fool All of the People All of the Time?”
Journal of Money, Credit and Banking, 4 (May 1972), 426-30.
Journal of Monetary Economics, 3 (July 1977), 375-77.
Journal of Political Economy, 64 (April 1956), 93-110; P. Cagan, “The Monetary Dynamics of Hyperinflation,” in Milton Friedman, ed.,
Studies in the Quantity Theory of Money (Chicago: University of Chicago Press, 1956), pp. 25-117; and Edward Tower, “More on the Welfare Cost of Inflationary Finance,”
Journal of Money, Credit and Banking, 9 (November 1971), 850-60.
Dm is tangential to a rectangular hyperbola that has as its vertical and horizontal axes the ordinate and zero-inflation or $1 line, respectively, in Figure 6.3. The true revenue-maximizing rate is determined where
Dm is tangential to a rectangular hyperbola that has as its vertical and horizontal axes the ordinate and abscissa, respectively, in Figure 6.3. The latter rate must lie below Bailey’s, since the latter hyperbola lies everywhere below the former.
Public Finance in Democratic Process (Chapel Hill: University of North Carolina Press, 1967), chap. 10.
Swedish Journal of Economics, 75 (March 1973), 67-82; and Jeremy J. Siegel, “A Note on Optimal Taxation and the Optimal Rate of Inflation,”
Journal of Monetary Economics, 4 (April 1978), 297-305.

