Empirics of Economic Growth

Since the late 1980s, economists have done extensive work on the determinants of economic growth. As yet, however, there are few widely agreed-on results. The lack of consensus is unfortunate because increasing the growth rates of the world’s many poor countries is a primary global policy goal. We do have at least two natural experiments in which a single nation was bisected by very different forms of governments: the two Germanys from the end of World War II to reunification in 1991, and the two Koreas. In both cases, the government that allowed private property and free (at least compared with its counterpart government) enterprise oversaw an economic “miracle,” while the more totalitarian governments in the pairings each produced decades of stagnation and poverty. Because, in each case, the people and their situations were so similar before the change that split them up, we get as close as we can ever get in the real world to a laboratory experiment without a laboratory—a fact that makes these findings significant. Economists know that there is some level of government intervention so great that it stifles economic growth, causing economies under it to do poorly.

But when economists use statistical analysis on large samples, other differences between countries that are hard to measure (e.g., culture) can be relevant, and the results are not as straightforward. We can show that factors such as private property rights and lack of corruption (or, as it is sometimes called, the “rule of law”) are strongly correlated with high income, but it is difficult to show that they are correlated with current growth. More on that later.

What do economists know about the causes of growth? Begin by looking at the world income distribution in the year 2000. Here, countries are the unit of analysis, which means that Uganda counts as much as China, despite China’s much greater population. Most economists take this approach, although some look at either population weighted distributions or worldwide distributions of individuals’ incomes.1

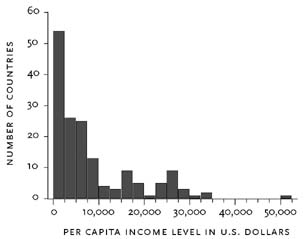
Figure 1 displays the distribution of per capita national income in U.S. dollars adjusted for deviations from purchasing power parity for 185 countries in the year 2000. The data are from the World Bank’s “World Development Indicators” online database. Ignoring the extreme outlier of Luxembourg (the $51,000 observation), the income ratio between the second-highest-income country (the United States) and the lowest-income country is about 77. There are 31 countries in the sample whose incomes are less than 5 percent of U.S. income, and 70 countries with incomes less than 10 percent of U.S. income. Income gaps this large are unprecedented in history; that is to say, the cross-country pattern of per capita incomes is diverging over time. In 1870, the corresponding income ratio was around 9, while in 1960 it was around 50.2

More specifically, the twenty-two highest-income countries in 1960 saw their average incomes relative to the United States rise slightly, from 69.4 percent of the U.S. level to 72.1 percent, a gain of almost 4 percent. A sample of forty-one sub-Saharan African countries saw their average relative income fall from 12 percent of the U.S. level in 1960 to 7.2 percent of the U.S. level in 2000, an average decline of 40 percent.3 In a sample of twenty-two Latin American countries, the average country income relative to the United States fell from 27.4 percent in 1960 to 17.4 percent in 2000, about a 35 percent decline. Even Chile, a success story in the region, saw its relative level fall slightly, from 31.4 percent to 29.8 percent.4 Only a sample of sixteen Asian countries shows catch-up, with their relative average income levels more than doubling, from 11.4 percent of the U.S. level to 26.4 percent.

Consider an illustration of the importance of raising growth rates. In 1960, Bolivia ($2,354) and Malaysia ($2,120) had roughly equal per capita incomes. Over the next forty years, however, Malaysia grew at an average annual rate of about 9 percent while Bolivia’s growth rate was a mere 0.5 percent. The result is that in 2000, Malaysia ($9,920) had a per capita income more than 3.5 times that of Bolivia ($2,724). Given the large number of poor countries in the world that are not currently growing much, knowing what a country can do to grow faster is vital.

At first blush, finding the determinants of growth seems simple. We simply need to figure out what the Asian countries did that Latin American and sub-Saharan African countries failed to do. Yet this task has not been easy because not all fast-growing countries have identical policies, and high-growth and low-growth countries sometimes have similar policies.

Before discussing numbers and results, though, let us examine the policy advice one would get from the most well-known and widely used theoretical model of economic growth, the neoclassical growth model (often called the Solow model after Nobel laureate Robert Solow’s fundamental work). The Solow model implies that if a country’s national saving rate rises, growth will temporarily rise above its long-run rate as the economy shifts to its new equilibrium. However, long-run equilibrium growth is independent of the saving rate or the population growth rate. If all countries have access to the same technology, all should have the same steady-state (long-run) growth rate.5 If a country raises its investment rate, it will experience a period of higher-than-normal growth as the economy adjusts to its new, higher growth path; but once the adjustment has occurred, growth will revert to the steady-state level. The model, then, has two predictions. First, countries with better policies should be richer; second, countries that, for whatever reason, are far away from their steady-state income level will grow faster than countries closer to their own (possibly different) steady-state income levels.

N. G. Mankiw, David Romer, and David Weil (1992) modified the neoclassical model by adding human capital as another input into the production of national income. In this so-called augmented Solow model, equilibrium income depends on the rate of investment in education as well as the physical capital investment rate. This opens another avenue for policy to affect wealth, as policies that increase educational investments will also make a country permanently richer and will temporarily raise its growth rate in the transition period to the new equilibrium.

Mankiw, Romer, and Weil also provided a statistical test of their model, measuring human capital investment by secondary-school enrollment rates. In their sample, this variable, a physical investment variable, and a variable related to population growth explained more than 80 percent of the cross-country variation in income. They also calculated that the rate at which a country approaches its steady state is fairly slow; only about 2 percent of the gap between the initial equilibrium and the new one is eliminated per year. This rate is generally referred to as the speed of convergence, though we should remember that the convergence concept here is conditional (relative to a country’s individual steady state) rather than absolute (catching up to the richest countries). In a series of empirical papers, Robert Barro and Xavier Sala-I-Martin (1992) obtained a 2 percent convergence rate in a wide variety of samples, but even this finding has been challenged on the grounds that the studies are done with “time averaging.” A numerical example illustrates the problem. Suppose that country A’s annual growth rate over twenty years averages 3.5 percent and its investment rate averages 15 percent. Suppose that country B’s annual growth rate over the same twenty years averages 5 percent and its investment rate averages 20 percent. Then a study of these countries will find a positive relationship between investment and growth. But what if we look beneath the averages and find that for the first ten years in country A, growth was 5 percent and the investment rate was only 10 percent and that for the next ten years, growth was down to 2 percent while the investment rate was up to 20 percent? Similarly, in country B, for the first ten years growth was 8 percent and the investment rate was 15 percent and for the next ten years, growth was down to 2 percent and the investment rate was up to 25 percent. Then for each country there would be a negative relationship between the investment rate and economic growth and “time averaging” would hide this true relationship. Most of the work finding 2 percent convergence is, unfortunately, based on time averaging.

Empirical studies of countries’ growth over time—that is, studies that avoid the time-averaging problem—have shown two main differences from the work described above. First, education is generally not found to be a significant determinant of growth. This was shown first by Nazrul Islam (1995) and well documented by Lant Pritchett (2001). Second, the convergence rate is generally estimated to be much higher than 2 percent. Islam calculated convergence rates of 4 to 6 percent, while F. Caselli, G. Esquivel, and F. Lefort (1996) obtained rates above 10 percent.

Besides potential inappropriate time averaging, there is another problem with studying countries at a point in time. Using only one observation per country in a statistical analysis requires including a large number of countries. Yet, many studies have shown that the parameters of empirical growth models vary widely across groups of countries.6 This can cause serious problems for studying a cross section of countries at a point in time. Perhaps the most serious problem is that once the rich countries are removed from a sample, there is very little evidence of conditional convergence for the rest of the countries when one allows a time dimension in the model.

A third statistical issue that makes empirical growth research problematic is the problem of reverse causality: we are seldom sure whether the variables expected to cause growth actually do so or are themselves caused by growth. For example, some economists claim that financial development helps growth, but others argue that economic growth itself causes financial development. The same argument could be made for variables like investment, political turmoil, and even international trade. While there are statistical techniques for addressing this issue, they are especially difficult to employ in growth models, where it is hard to determine that a particular variable can legitimately be excluded.

If one ignores all three of these issues—that is to say, if one estimates cross-sectional regressions on a wide range of disparate countries and makes no allowance for the possibility of reverse causality—a few variables seem to have a significant effect on growth. Sala-I-Martin (1997) undertakes this experiment in “I Just Ran Two Million Regressions.” He considers sixty-three variables that might potentially explain growth. He finds higher growth in countries that have been open to trade (as measured by the Sachs and Warner [1995] index) longer, that abide by the “rule of law,” and that are more capitalistic. On the other side, he finds growth to be negatively associated with revolutions, coups, and wars. However, it is difficult to take these results at face value. Consider the finding on capitalism. Sala-I-Martin’s variable for growth is the average per capita growth rate from 1960 to 1992. But his variable for capitalism is from a 1994 Freedom House document (Freedom House is an organization that rates the freedom of various countries). Literally, then, we are being told that being capitalist in the early 1990s affected a country’s growth rate in the 1950s, 1960s, and 1970s. The same type of difficulty arises in the use of the Sachs-Warner trade measure, which is constructed with data collected from 1950 to 1990. To make policy recommendations, we need to know that being open to trade today, or being capitalistic today, will increase growth in future years, and the empirical work so far does not clearly establish that claim.

All that being said, the policy variables that seem most robustly related to growth are sound macroeconomic policies (mainly stable and reasonably low inflation), openness to trade, institutional quality (i.e., little government corruption), and financial development.

One of the most interesting recent approaches to understanding what causes sustained increases in economic growth is the work by Ricardo Hausmann, Lant Pritchett, and Dani Rodrik (2004), who studied eighty-three cases in which a country rapidly increased its growth rate and sustained the increase for at least eight years. Their most statistically significant results are that a financial liberalization raises the probability of a growth increase by around 7 percent, and that a political regime change toward autocracy (from democracy or less-strict autocracy) raises the probability of increased growth by almost 11 percent. Most growth increases (which they call “growth accelerations”) are unpredictable, however, and as they put it, “the vast majority of growth accelerations are unrelated to standard determinants such as political change and economic reform, and most instances of economic reform do not produce growth accelerations.”7

Two popular candidates for factors important to economic growth are property rights and political rights. A good measure of property rights is available from the Heritage Foundation’s Index of Economic Freedom, which ranks countries from one (excellent property rights, fast enforcement, no corruption, no expropriation) to five (little to no secure private property, high corruption, mostly state-owned resources, frequent expropriation).8 A measure of political rights is taken from Freedom House’s survey of freedom in the world, which ranks countries from one (free and fair elections, a competitive opposition, respect for minority political groups) to seven (political rights largely absent, oppressive regime).9

We can take these rankings for 2000 and merge them with real per capita GDP data (again adjusted for deviations from PPP) from the Penn World Tables. This creates a sample of 120 countries for the growth rate and 123 for the 2000 income level. Doing so shows two main things: (1) for economic well-being, secure property rights are more important than political rights; and, (2) these variables explain income levels but not growth rates.

The simple correlation between the property rights variable and per capita income is −.78, while the correlation between the political rights variable and per capita income is −.59. (The negatives occur because for both measures, whether of political rights or property rights, higher numbers mean less respect for rights.) A zero would indicate no correlation between the variables, and −1 indicates perfect negative correlation. Both the correlations are sizable and significantly different from zero, but the two explanatory variables are also significantly correlated with each other (the property rights − political rights correlation is .71). A basic multiple regression can sort out the independent effects of the two variables on income. The results are as follows:

The numbers below the coefficients are their estimated standard errors; they imply that property rights is a highly significant variable, and, when it is included in the model, political rights is not significantly partially correlated with income. This simple equation accounts for about 61 percent of the variation in incomes across countries. Taken literally, every step of improvement in the secure property rights scale raises a country’s per capita income by more than $5,000.10

For growth, as opposed to income level, the picture is quite different. The correlation between property rights and average annual growth from 1995 to 2000 is .02, and the political rights–average growth correlation is .06. In a multiple regression of income growth on the two variables, both variables are completely insignificant, either jointly or individually. Property rights do seem to matter, but mainly for being rich and not for causing higher-than-average current growth. Note that this is exactly what the neoclassical growth model would predict, in that a policy that raises savings and investment (improving property rights) raises equilibrium income but not the long-run growth rate.

Finally, for those looking for further reading on this topic, a good starting point is the work of economists such as Stephen Durlauf, Peter Klenow, Lant Pritchett, and Dani Rodrik.11