Principles of Economics
By Alfred Marshall
Economic conditions are constantly changing, and each generation looks at its own problems in its own way. In England, as well as on the Continent and in America, Economic studies are being more vigorously pursued now than ever before; but all this activity has only shown the more clearly that Economic science is, and must be, one of slow and continuous growth. Some of the best work of the present generation has indeed appeared at first sight to be antagonistic to that of earlier writers; but when it has had time to settle down into its proper place, and its rough edges have been worn away, it has been found to involve no real breach of continuity in the development of the science. The new doctrines have supplemented the older, have extended, developed, and sometimes corrected them, and often have given them a different tone by a new distribution of emphasis; but very seldom have subverted them…. [From the Preface to the First Edition]
First Pub. Date
1890
Publisher
London: Macmillan and Co., Ltd.
Pub. Date
1920
Comments
8th edition
Copyright
The text of this edition is in the public domain.
- Preface
- Bk.I,Ch.I
- Bk.I,Ch.II
- Bk.I,Ch.III
- Bk.I,Ch.IV
- Bk.II,Ch.I
- Bk.II,Ch.II
- Bk.II,Ch.III
- Bk.II,Ch.IV
- Bk.III,Ch.I
- Bk.III,Ch.II
- Bk.III,Ch.III
- Bk.III,Ch.IV
- Bk.III,Ch.V
- Bk.III,Ch.VI
- Bk.IV,Ch.I
- Bk.IV,Ch.II
- Bk.IV,Ch.III
- Bk.IV,Ch.IV
- Bk.IV,Ch.V
- Bk.IV,Ch.VI
- Bk.IV,Ch.VII
- Bk.IV,Ch.VIII
- Bk.IV,Ch.IX
- Bk.IV,Ch.X
- Bk.IV,Ch.XI
- Bk.IV,Ch.XII
- Bk.IV,Ch.XIII
- Bk.V,Ch.I
- Bk.V,Ch.II
- Bk.V,Ch.III
- Bk.V,Ch.IV
- Bk.V,Ch.V
- Bk.V,Ch.VI
- Bk.V,Ch.VII
- Bk.V,Ch.VIII
- Bk.V,Ch.IX
- Bk.V,Ch.X
- Bk.V,Ch.XI
- Bk.V,Ch.XII
- Bk.V,Ch.XIII
- Bk.V,Ch.XIV
- Bk.V,Ch.XV
- Bk.VI,Ch.I
- Bk.VI,Ch.II
- Bk.VI,Ch.III
- Bk.VI,Ch.IV
- Bk.VI,Ch.V
- Bk.VI,Ch.VI
- Bk.VI,Ch.VII
- Bk.VI,Ch.VIII
- Bk.VI,Ch.IX
- Bk.VI,Ch.X
- Bk.VI,Ch.XI
- Bk.VI,Ch.XII
- Bk.VI,Ch.XIII
- Appendix A
- Appendix B
- Appendix C
- Appendix D
- Appendix E
- Appendix F
- Appendix G
- Appendix H
- Appendix I
- Appendix J
- Appendix K
- Bk.App,Ch.L
- Bk.App,Ch.M
THE THEORY OF MONOPOLIES.
BOOK V, CHAPTER XIV
§ 1. It has never been supposed that the monopolist in seeking his own advantage is naturally guided in that course which is most conducive to the wellbeing of society regarded as a whole, he himself being reckoned as of no more importance than any other member of it. The doctrine of Maximum Satisfaction has never been applied to the demand for and supply of monopolized commodities. But there is much to be learnt from a study of the relations in which the interests of the monopolist stand to those of the rest of society, and of the general conditions under which it might be possible to make arrangements more beneficial to society as a whole than those which he would adopt if he consulted only his own interests: and with this end in view we are now to seek for a scheme for comparing the relative quantities of the benefits which may accrue to the public and to the monopolist from the adoption of different courses of action by him.
In a later volume a study will be made of the Protean shapes of modern trade combinations and monopolies, some of the most important of which, as for example “Trusts,” are of very recent growth. At present we consider only those general causes determining monopoly values, that can be traced with more or less distinctness in every case in which a single person or association of persons has the power of fixing either the amount of a commodity that is offered for sale or the price at which it is offered.
§ 2. The
primâ facie interest of the owner of a monopoly is clearly to adjust the supply to the demand, not in such a way that the price at which he can sell his commodity shall just cover its expenses of production, but in such a way as to afford him the greatest possible total net revenue.
But here we meet with a difficulty as to the meaning of the term Net revenue. For the supply price of a freely-produced commodity includes normal profits; the whole of which, or at all events what remains of them after deducting interest on the capital employed and insurance against loss, is often classed indiscriminately as net revenue. And when a man manages his own business, he often does not distinguish carefully that portion of his profits, which really is his own earnings of management, from any exceptional gains arising from the fact that the business is to some extent of the nature of a monopoly.
This difficulty however is in a great measure avoided in the case of a public company; where all, or nearly all, the expenses of management are entered in the ledger as definite sums, and are subtracted from the total receipts of the company before its net income is declared.
The net income divided among the shareholders includes interest on the capital invested and insurance against risk of failure, but little or no earnings of management; so that the amount by which the dividends are in excess of what may fairly be allowed as interest and insurance, is the
Monopoly Revenue which we are seeking.
Since then it is much easier to specify exactly the amount of this net revenue when a monopoly is owned by a public company than when it is owned by an individual or private firm, let us take as a typical instance the case of a gas company that has the monopoly of the supply of gas to a town. For the sake of simplicity the company may be supposed to have already invested the whole of its own capital in fixed plant, and to borrow any more capital, that it may want to extend its business, on debentures at a fixed rate of interest.
§ 3. The demand schedule for gas remains the same as it would be if gas were a freely-produced commodity; it specifies the price per thousand feet at which consumers in the town will among them use any given number of feet. But the supply schedule must represent the normal expenses of production of each several amount supplied; and these include interest on all its capital, whether belonging to its shareholders or borrowed on debentures, at a fixed normal rate; they include also the salaries of its directors, and permanent officials, adjusted (more or less accurately) to the work required of them, and therefore increasing with an increase in the output of gas. A
monopoly revenue schedule may then be constructed thus:—Having set against each several amount of the commodity its demand price, and its supply price estimated on the plan just described, subtract each supply price from the corresponding demand price and set the residue in the monopoly revenue column against the corresponding amount of the commodity.
Thus for instance if a thousand million feet could be sold annually at a price of 3
s. per thousand feet, and the supply price for this amount were 2
s. 9
d. per thousand feet, the monopoly revenue schedule would show 3
d. against this amount; indicating an aggregate net revenue when this amount was sold, of three million pence, or £12,500. The aim of the company, having regard only to their own immediate dividends, will be to fix the price of their gas at such a level as to make this aggregate net revenue the largest possible
*130.
§ 4. Now suppose that a change takes place in the conditions of supply; some new expense has to be incurred, or some old expense can be avoided; or perhaps a new tax is imposed on the undertaking or a bounty is awarded to it.
First let this increase or diminution of the expenses be a fixed sum, bearing on the undertaking as one undivided whole and not varying with the amount of the commodity produced. Then, whatever be the price charged and the amount of the commodity sold, the monopoly revenue will be increased or diminished, as the case may be, by this sum; and therefore that selling price which afforded the maximum monopoly revenue before the change will afford it afterwards; the change therefore will not offer to the monopolist any inducement to alter his course of action. Suppose for instance that the maximum monopoly revenue is got when twelve hundred million cubic feet are sold annually; and that this is done when the price is fixed at 30
d. per thousand feet: suppose that the expenses of production for this amount are at the rate of 26
d., leaving a monopoly revenue at the rate of four pence per thousand feet, that is £20,000 in all. This is its maximum value: if the company fixed the price higher at, say, 31
d. and sold only eleven hundred million feet, they would perhaps get a monopoly revenue at the rate of 4.2 pence per thousand feet, that is £19,250 in all; while in order to sell thirteen hundred millions they would have to lower their price to, say, 28
d. and would get a monopoly revenue at the rate of perhaps 3×6
d. per thousand feet, that is £19,500 in all. Thus by fixing the price at 30
d. they get £750 more than by fixing it at 31
d., and £500 more than by fixing it at 28
d. Now let a tax of £10,000 a year be levied on the gas company as a fixed sum independent of the amount they sell. Their monopoly revenue will become £10,000 if they charge 30
d., £9,250 if they charge 31
d., and £9,500 if they charge 28
d. They will therefore continue to charge 30
d.
The same is true of a tax or a bounty proportioned not to the gross receipts of the undertaking, but to its monopoly revenue. For suppose next that a tax is levied, not of one fixed sum, but a certain percentage, say 50 per cent. of the monopoly revenue. The company will then retain a monopoly revenue of £10,000 if they charge 30
d., of £9,625 if they charge 31
d., and of £9,750 if they charge 28
d. They will therefore still charge 30
d.*131
On the other hand a tax proportional to the amount produced gives an inducement to the monopolist to lessen his output and raise his price. For by so doing he diminishes his expenses. And the excess of total receipts over total outlay may therefore be now increased by a diminution of output; though before the imposition of the tax it would have been lessened. Further, if before the imposition of the tax the net revenue was only a little greater than that which would have been afforded by much smaller sales, then the monopolist would gain by reducing his production very greatly; and hence in such cases as this, the change is likely to cause a very great diminution of production and rise of price. The opposite effects will be caused by a change which diminishes the expense of working the monopoly by a sum that varies directly with the amount produced under it.
In the last example, for instance, a tax of 2
d. on each thousand feet sold would have reduced the monopoly revenue to £10,083 if the company charged 31
d. per thousand feet and therefore sold eleven hundred millions; to £10,000 if they charged 30
d. and therefore sold twelve hundred millions, and to £8,666 if they charged 28
d. and therefore sold thirteen hundred million feet. Therefore the tax would induce the company to raise the price to something higher than 30
d.; they would perhaps go to 31
d., perhaps somewhat higher; for the figures before us do not show exactly how far it would be their interest to go.
On the other hand, if there were a bounty of 2
d. on the sale of each thousand feet, the monopoly revenue would rise to £28,416 if they charged 31
d., to £30,000 if they charged 30
d., and to £30,333 if they charged 28
d.: it would therefore cause them to lower the price. And of course the same result would follow from an improvement in the method of making gas, which lowered its cost of production to the monopolist company by 2
d. per 1000 feet
*132.
§ 5. The monopolist would lose all his monopoly revenue if he produced for sale an amount so great that its supply price, as here defined, was equal to its demand price: the amount which gives the maximum monopoly revenue is always considerably less than that. It may therefore appear as though the amount produced under a monopoly is always less and its price to the consumer always higher than if there were no monopoly. But this is not the case.
For when the production is all in the hands of one person or company, the total expenses involved are generally less than would have to be incurred if the same aggregate production were distributed among a multitude of comparatively small rival producers. They would have to struggle with one another for the attention of consumers, and would necessarily spend in the aggregate a great deal more on advertising in all its various forms than a single firm would; and they would be less able to avail themselves of the many various economies which result from production on a large scale. In particular they could not afford to spend as much on improving methods of production and the machinery used in it, as a single large firm which knew that it was certain itself to reap the whole benefit of any advance it made.
This argument does indeed assume the single firm to be managed with ability and enterprise, and to have an unlimited command of capital—an assumption which cannot always be fairly made. But where it can be made, we may generally conclude that the supply schedule for the commodity, if not monopolized, would show higher supply prices than those of our monopoly supply schedule; and therefore the equilibrium amount of the commodity produced under free competition would be less than that for which the demand price is equal to the monopoly supply price
*133.
One of the most interesting and difficult applications of the theory of monopolies is to the question whether the public interest is best served by the allotment of a distinct basin to each great railway, and excluding competition there. For the proposal it is urged that a railway can afford to carry two million passengers, or tons of goods, cheaper than one million: and that a division of the public demand between two lines will prevent either of them from offering a cheap service. It must be admitted that, other things being equal, the “monopoly revenue price” fixed by a railway will be lowered by every increase in the demand for its services, and
vice versâ. But, human nature being what it is, experience has shown that the breaking of a monopoly by the opening out of a competing line accelerates, rather than retards the discovery by the older line that it can afford to carry traffic at lower rates. There still remains the suggestion that after a while the railways will combine and charge the public with the expense wasted on duplicating the services. But this again only opens out new matters of controversy. The theory of monopolies starts rather than solves practical issues such as these: and we must defer their study
*134.
§ 6. So far we have supposed the owner of a monopoly to fix the price of his commodity with exclusive reference to the immediate net revenue which he can derive from it. But, in fact, even if he does not concern himself with the interests of the consumers, he is likely to reflect that the demand for a thing depends in a great measure on people’s familiarity with it; and that if he can increase his sales by taking a price a little below that which would afford him the maximum net revenue, the increased use of his commodity will before long recoup him for his present loss. The lower the price of gas, the more likely people are to have it laid on to their houses; and when once it is there, they are likely to go on making some use of it, even though a rival, such as electricity or mineral oil, may be competing closely with it. The case is stronger when a railway company has a practical monopoly of the transport of persons and goods to a sea-port, or to a suburban district which is as yet but partly built over; the railway company may then find it worth while, as a matter of business, to levy charges much below those which would afford the maximum net revenue, in order to get merchants into the habit of using the port, to encourage the inhabitants of the port to develop their docks and warehouses; or to assist speculative builders in the new suburb to build houses cheaply and to fill them quickly with tenants, thus giving to the suburb an air of early prosperity which goes far towards insuring its permanent success. This sacrifice by a monopolist of part of his present gains in order to develop future business differs in extent rather than kind from the sacrifices which a young firm commonly makes in order to establish a connection.
In such cases as these a railway company though not pretending to any philanthropic motives, yet finds its own interests so closely connected with those of the purchasers of its services, that it gains by making some temporary sacrifice of net revenue with the purpose of increasing consumers’ surplus. And an even closer connection between the interests of the producers and the consumers is found when the landowners of any district combine to make a branch railway through it, without much hope that the traffic will afford the current rate of interest on the capital which they invest—that is, without much hope that the monopoly revenue of the railway, as we have defined it, will be other than a negative quantity—but expecting that the railway will add so much to the value of their property as to make their venture on the whole a profitable one. And when a municipality undertakes the supply of gas or water, or facilities for transport by improved roads, by new bridges, or by tramways, the question always arises whether the scale of charges should be high, so as to afford a good net revenue and relieve the pressure on the rates; or should be low, so as to increase consumers’ surplus.
§ 7. It is clear then that some study is wanted of calculations by which a monopolist should govern his actions, on the supposition that he regards an increase of consumers’ surplus as equally desirable to him, if not with an equal increase of his own monopoly revenue, yet with an increase, say, one-half or one-quarter as great.
If the consumers’ surplus which arises from the sale of the commodity at any price, is added to the monopoly revenue derived from it, the sum of the two is the money measure of the net benefits accruing from the sale of the commodity to producers and consumers together, or as we may say the
total benefit of its sale. And if the monopolist regards a gain to the consumers as of equal importance with an equal gain to himself, his aim will be to produce just that amount of the commodity which will make this total benefit a maximum
*135.
But it will seldom happen that the monopolist can and will treat £1 of consumers’ surplus as equally desirable with £1 of monopoly revenue. Even a government which considers its own interests coincident with those of the people has to take account of the fact that, if it abandons one source of revenue, it must in general fall back on others which have their own disadvantages. For they will necessarily involve friction and expense in collection, together with some injury to the public, of the kind which we have described as a loss of consumers’ surplus: and they can never be adjusted with perfect fairness, especially when account is taken of the unequal shares that different members of the community will get of the benefits for the sake of which it is proposed that the government should forego some of its revenue.
Suppose then that the monopolist makes a compromise, and reckons £1 of consumers’ surplus as equivalent to say 10
s. of monopoly revenue. Let him calculate the monopoly revenue to be got from selling his commodity at any given price, and to it let him add one half the corresponding consumers’ surplus: the sum of the two may be called the
compromise benefit; and his aim will be to fix on that price which will make the compromise benefit as large as possible
*136.
The following general results are capable of exact proof; but on a little consideration they will appear so manifestly true as hardly to require proof. Firstly, the amount which the monopolist will offer for sale will be greater (and the price at which he will sell it will be less) if he is to any extent desirous to promote the interests of consumers than if his sole aim is to obtain the greatest possible monopoly revenue; and secondly, the amount produced will be greater (and the selling price will be less) the greater be the desire of the monopolist to promote the interests of consumers;
i.e. the larger be the percentage of its actual value at which he counts in consumers’ surplus with his own revenue
*137.
§ 8. Not many years ago it was commonly argued that: “An English ruler, who looks upon himself as the minister of the race he rules, is bound to take care that he impresses their energies in no work that is not worth the labour that is spent upon it, or—to translate the sentiment into plainer language—that he engages in nothing that will not produce an income sufficient to defray the interest on its cost
*138.” Such phrases as this may sometimes have meant little more than that a benefit which consumers were not willing to purchase at a high price and on a large scale, was likely to exist for the greater part only in the specious counsels of those who had some personal interest in the proposed undertakings; but probably they more often indicated a tendency to under-estimate the magnitude of that interest which consumers have in a low price, and which we call consumers’ surplus
*139.
One of the chief elements of success in private business is the faculty of weighing the advantages and disadvantages of any proposed course, and of assigning to them their true relative importance. He who by practice and genius has acquired the power of attributing to each factor its right quantity, is already well on the way to fortune; and the increase in the efficiency of our productive forces is in a great measure due to the large number of able minds who are devoting themselves ceaselessly to acquiring these business instincts. But unfortunately the advantages thus weighed against one another are nearly all regarded from one point of view, that of the producer; and there are not many who concern themselves to weigh against one another the relative quantities of the interests which the consumers and the producers have in different courses of action. For indeed the requisite facts come within the direct experience of only a very few persons, and even in the case of those few, only to a very limited extent and in a very imperfect way. Moreover when a great administrator has acquired those instincts with regard to public interests which able business men have with regard to their own affairs, he is not very likely to be able to carry his plans with a free hand. At all events in a democratic country no great public undertaking is secure of being sustained on consistent lines of policy, unless its advantages can be made clear, not only to the few who have direct experience of high public affairs, but also to the many who have no such experience and have to form their judgment on the materials set before them by others.
Judgments of this kind must always be inferior to those which an able business man forms, by the aid of instincts based on long experience with regard to his own business. But they may be made much more trustworthy than they are at present, if they can be based on statistical measures of the relative quantities of the benefits and the injuries which different courses of public action are likely to cause to the several classes of the community. Much of the failure and much of the injustice, in which the economic policies of governments have resulted, have been due to the want of statistical measurement. A few people who have been strongly interested on one side have raised their voices loudly, persistently and all together; while little has been heard from the great mass of people whose interests have lain in the opposite direction; for, even if their attention has been fairly called to the matter, few have cared to exert themselves much for a cause in which no one of them has more than a small stake. The few therefore get their way, although if statistical measures of the interests involved were available, it might prove that the aggregate of the interests of the few was only a tenth or a hundredth part of the aggregate of the interests of the silent many.
No doubt statistics can be easily misinterpreted; and are often very misleading when first applied to new problems. But many of the worst fallacies involved in the misapplications of statistics are definite and can be definitely exposed, till at last no one ventures to repeat them even when addressing an uninstructed audience: and on the whole arguments which can be reduced to statistical forms, though still in a backward condition, are making more sure and more rapid advances than any others towards obtaining the general acceptance of all who have studied the subjects to which they refer. The rapid growth of collective interests, and the increasing tendency towards collective action in economic affairs, make it every day more important that we should know what quantitative measures of public interests are most needed and what statistics are required for them, and that we should set ourselves to obtain these statistics.
It is perhaps not unreasonable to hope that as time goes on, the statistics of consumption will be so organized as to afford demand schedules sufficiently trustworthy, to show in diagrams that will appeal to the eye, the quantities of consumers’ surplus that will result from different courses of public and private action. By the study of these pictures the mind may be gradually trained to get juster notions of the relative magnitudes of the interests which the community has in various schemes of public and private enterprise; and sounder doctrines may replace those traditions of an earlier generation, which had perhaps a wholesome influence in their time, but which damped social enthusiasm by throwing suspicion on all projects for undertakings by the public on its own behalf which would not show a balance of direct pecuniary profit.
The practical bearings of many of the abstract reasonings in which we have recently been engaged will not be fully apparent till we approach the end of this treatise. But there seemed to be advantages in introducing them thus early, partly because of their close connection with the main theory of equilibrium of demand and supply, and partly because they throw side lights on the character and the purposes of that investigation of the causes which determine distribution on which we are about to enter.
§ 9. So far it has been assumed that the monopolist can buy and sell freely. But in fact monopolistic combinations in one branch of industry foster the growth of monopolistic combinations in those which have occasion to buy from or sell to it: and the conflicts and alliances between such associations play a rôle of ever increasing importance in modern economics. Abstract reasoning of a general character has little to say on the subject. If two absolute monopolies are complementary, so that neither can turn its products to any good account, without the other’s aid, there is no means of determining where the price of the ultimate product will be fixed. Thus if we supposed, following Cournot’s lead, that copper and zinc were each of them useless except when combined to make brass: and if we supposed that one man,
A, owned all the available sources of supply of copper; while another,
B, owned all those of zinc; there would then be no means of determining beforehand what amount of brass would be produced, nor therefore the price at which it could be sold. Each would try to get the better of the other in bargaining; and though the issue of the contest would greatly affect the purchasers, they would not be able to influence it
*140.
Under the conditions supposed,
A could not count on reaping the whole, nor even any share at all of the benefit, from increased sales, that would be got by lowering the price of copper in a market in which the price of zinc was fixed by natural causes rather than strategical higgling and bargaining. For, if he reduced his price,
B might take the action as a sign of commercial weakness, and raise the price of zinc; thus causing
A to lose both on price and on amount sold. Each would therefore be tempted to bluff the other; and consumers might find that less brass was put on the market, and that therefore a higher price could be exacted for it, than if a single monopolist owned the whole supplies both of copper and of zinc: for he might see his way to gaining in the long run by a low price which stimulated consumption. But neither
A nor
B could reckon on the effects of his own action, unless the two came together and agreed on a common policy: that is unless they made a partial, and perhaps temporary fusion of their monopolies. On this ground, and because monopolies are likely to disturb allied industries it may reasonably be urged that the public interest generally requires that complementary monopolies should be held in a single hand.
But there are other considerations of perhaps greater importance on the other side. For in real life there are scarcely any monopolies as absolute and permanent as that just discussed. On the contrary there is in the modern world an ever increasing tendency towards the substitution of new things and new methods for old, which are not being developed progressively in the interests of consumers; and the direct or indirect competition thus brought to bear is likely to weaken the position of one of the complementary monopolies more than the other. For instance if there be only one factory for spinning and only one for weaving in a small isolated country, it may be for the time to the public interest that the two should be in the same hands. But the monopoly so established will be much harder to shake than would either half of it separately. For a new venturer might push his way into the spinning business and compete with the old spinning mill for the custom of the old weaving sheds.
Consider again a through route, partly by rail and partly by sea, between two great centres of industry. If competition on either half of the route were permanently impossible, it would probably be to the public interest that the ships and the railway line should be in the same hands. But as things are, no such general statement can be made. Under some conditions it is more to the public interest that they should be in one hand; under others, and those perhaps the conditions that occur the more frequently, it is in the long run to the public interest that they should remain in different hands.
Similarly the
primâ facie arguments in favour of the fusion of monopolistic cartels, or other associations, in complementary branches of industry, though often plausible and even strong, will generally be found on closer examination to be treacherous. They point to the removal of prominent social and industrial discords; but at the probable expense of larger and more enduring discords in the future
*141.
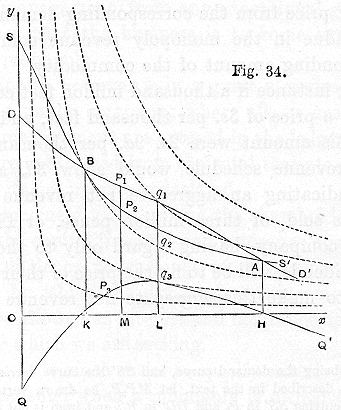 Thus
ThusDD‘ being the demand curve, and
SS‘ the curve corresponding to the supply schedule described in the text, let
MP2P1 be drawn vertically from any point
M in
Ox, cutting
SS‘ in
P2 and
DD‘ in
P1; and from it cut off
MP3 =
P2P1, then the locus of
P3 will be our third curve,
QQ‘, which we may call the
monopoly revenue curve. The supply price for a small quantity of gas will of course be very high; and in the neighbourhood of
Oy the supply curve will be above the demand curve, and therefore the net revenue curve will be below
Ox. It will cut
Ox in
K and again in
H, points which are vertically under
B and
A, the two points of intersection of the demand and supply curves. The maximum monopoly revenue will then be obtained by finding a point
q2 on
QQ‘ such that
Lq3 being drawn perpendicular to
Ox, OL ×
Lq3 is a maximum.
Lq3 being produced to cut
SS‘ in
q2 and
DD‘ in
q1, the company, if desiring to obtain the greatest immediate monopoly revenue, will fix the price per thousand feet at
Lq1, and consequently will sell
OL thousand feet; the expenses of production will be
Lq2 per thousand feet, and the aggregate net revenue will be
OL ×
q2q1, or which is the same thing
OL ×
Lq3.
The dotted lines in the diagram are known to mathematicians as rectangular hyperbolas; but we may call them
constant revenue curves: for they are such that if from a point on any one of them lines be drawn perpendicular to
Ox and
Oy respectively (the one representing revenue per thousand feet and the other representing the number of thousand feet sold), then the product of these will be a constant quantity for every point on one and the same curve. This product is of course a smaller quantity for the inner curves, those nearer
Ox and
Oy, than it is for the outer curves. And consequently since
P3 is on a smaller constant revenue curve than
q3 is,
OM ×
MP3 is less than
OL ×
Lq3. It will be noticed that
q3 is the point in which
QQ‘ touches one of these curves. That is,
q3 is on a larger constant revenue curve than is any other point on
QQ‘; and therefore
OL ×
Lq3 is greater than
OM ×
MP3, not only in the position given to
M in the figure, but also in any position that
M can take along
Ox. That is to say,
q3 has been correctly determined as the point on
QQ‘ corresponding to the maximum total monopoly revenue. And thus we get the rule:—If through that point in which
QQ‘ touches one of a series of constant revenue curves, a line be drawn vertically to cut the demand curve, then the distance of that point of intersection from
Ox will be the price at which the commodity should be offered for sale in order that it may afford the maximum monopoly revenue. See Note XXII. in the Mathematical Appendix.
fixed amount than that on which it lies. Therefore the maximum revenue point on the new monopoly revenue curve lies vertically below that on the old: that is, the selling price and the amount produced remain unchanged, and conversely with regard to a fixed bounty or other fixed diminution of aggregate working expenses. As to the effects of a tax proportional to monopoly revenue, see Note XXIII. in the Mathematical Appendix.
It should however be noticed that if a tax or other new additional expense exceeds the maximum monopoly revenue, it will prevent the monopoly from being worked at all; it will convert the price which had afforded the maximum monopoly revenue into the price which would reduce to a minimum the loss that would result from continuing to work the monopoly.
Much instruction is to be got by drawing diagrams to represent various conditions of demand and of (monopoly) supply, with the resultant shapes of the monopoly revenue curve. A careful study of the shapes thus obtained will give more assistance than any elaborate course of reasoning in the endeavour to realize the multiform action of economic forces in relation to monopolies. A tracing may be made on thin paper of the constant revenue curves in one of the diagrams; and this, when laid over a monopoly revenue curve, will indicate at once the point, or points, of maximum revenue. For it will be found, not only when the demand and supply curves cut one another more than once, but also when they do not, there will often be, as in
fig. 35, several points on a monopoly revenue curve at which it touches a constant revenue curve. Each of these points will show a true maximum monopoly revenue; but one of them will generally stand out pre-eminently as being on a larger constant revenue curve than any of the others and therefore indicating a larger monopoly revenue than they.
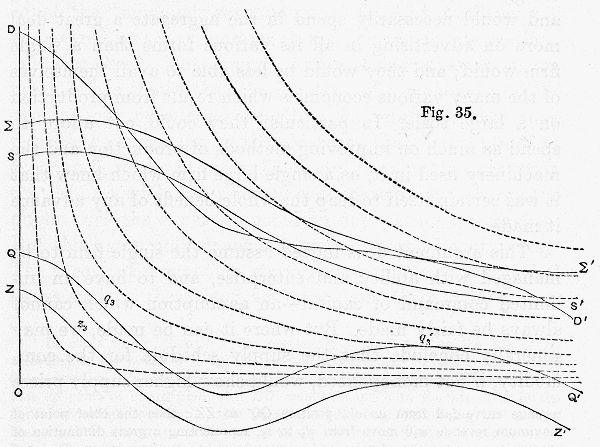
If it happens, as in fig. 35, that this chief maximum
q‘
3 lies a long way to the right of a smaller maximum
q3, then the imposition of a tax on the commodity, or any other change that raised its supply curve throughout, would lower by an equal amount the monopoly revenue curve. Let the supply curve be raised from
SS‘ to the position
SS‘; and in consequence let the monopoly revenue curve fall from its old position
QQ‘ to
ZZ‘; then the chief point of maximum revenue will move from
q‘
3 to
z3, representing a great diminution of production, a great rise of price and a great injury to the consumers. The converse effects of any change, such as a bounty on the commodity, which lowers its supply price throughout and raises the monopoly revenue curve, may be seen by regarding
ZZ‘ as the old and
QQ‘ as the new position of that curve. It will be obvious on a little consideration (but the fact may with advantage be illustrated by drawing suitable diagrams), that the more nearly the monopoly revenue curve approximates to the shape of a constant revenue curve, the greater will be the change in the position of the maximum revenue point which results from any given alteration in the expenses of production of the commodity generally. This change is great in fig. 35 not because
DD‘ and
SS‘ intersect more than once, but because two parts of
QQ‘, one a long way to the right of the other, lie in the neighbourhood of the same constant revenue curve.
L lies necessarily a good deal to the left of
H, according to the notation in
fig. 34; yet the supply curve for the commodity, if there were no monopoly, might lie so much above the present position of
SS‘ that its point of intersection with
DD‘ would lie much to the left of
A in the figure, and might not improbably lie to the left of
L. Something has already been said (IV. XI., XII.; and V. XI.), as to the advantages which a single powerful firm has over its smaller rivals in those industries in which the law of increasing return acts strongly; and as to the chance which it might have of obtaining a practical monopoly of its own branch of production, if it were managed for many generations together by people whose genius, enterprise and energy equalled those of the original founders of the business.
Giornale degli Economisti for Oct. 1897. But an inspection of
fig. 34 will show that a uniform raising of
DD‘ will push
L much to the right; and that the resulting position of
q1 will probably be lower than before. If, however, a new class of residents come into the district, who are so well to do, that their willingness to travel is very little affected by the railway charges, then the shape of
DD‘ will be altered; its left side will be raised more in proportion than its right; and the new position of
q1 may be higher than the old.
fig. 36DD‘,
SS‘, and
QQ‘ represent the demand, supply, and monopoly revenue curves drawn on the same plan as in
fig. 34. From
P1 draw
P1F perpendicular to
Oy; then
DFP1 is the consumers’ surplus derived from the sale of
OM thousand feet of gas at the price
MP1. In
MP1 take a point
P4 such that
OM ×
MP4 = the area
DFP1: then as
M moves from
O along
Ox,P4 will trace out our fourth curve,
OR, which we may call the
consumers’ surplus curve. (Of course it passes through
O, because when the sale of the commodity is reduced to nothing, the consumers’ surplus also vanishes.)
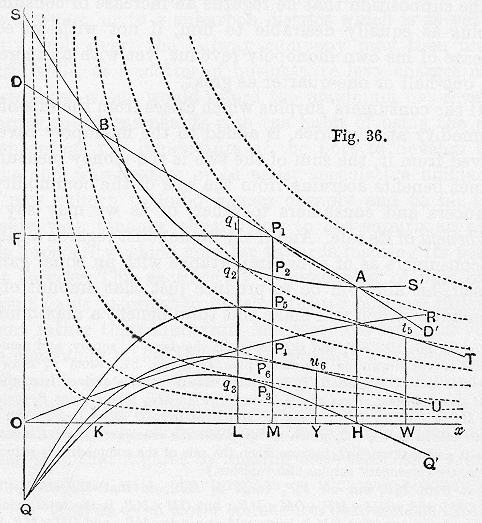
Next from
P3P1 cut off
P3P5 equal to
MP4, so that
MP5 =
MP3 +
MP Then
OM ×
MP5 =
OM ×
MP3 +
OM ×
MP4: but
OM ×
MP3 is the total monopoly revenue when an amount
OM is being sold at a price
MP1, and
OM ×
MP4 is the corresponding consumers’ surplus. Therefore
OM ×
MP5 is the sum of the monopoly revenue and the consumers’ surplus, that is the (money measure of the) total benefit which the community will derive from the commodity when an amount
OM is produced. The locus of
P5 is our fifth curve,
QT, which we may call the
total benefit curve. It touches one of the constant revenue curves at
t5, and this shows that the (money measure of the) total benefit is a maximum when the amount offered for sale is
OW; or, which is the same thing, when the price of sale is fixed at the demand price for
OW.
n of monopoly revenue,
n being a proper fraction, let us take a point
P6 in
P3P5 such that
P3P6 =
n·
P3P5, or, which is the same thing,
nMP4. Then
OM ×
MP6 =
OM ×
MP3, +
nOM ×
MP4; that is, it is equal to the monopoly revenue derived from selling an amount
OM of the commodity at the price
MP1, +
n times the consumers’ surplus derived from this sale: and is therefore the compromise benefit derived from that sale. The locus of
P6 is our sixth curve,
QU, which we may call the
compromise benefit curve. It touches one of the constant revenue curves in
u6; which shows that the compromise benefit attains its maximum when amount
OY is sold; or which is the same thing, when the selling price is fixed at the demand price for the amount
OY.
OYfig. 36 is always greater than
OL; and secondly, the greater
n is, the greater
OY is. (See Note XXIII.
bis in the Mathematical Appendix.)
The Times for July 30, 1874: they fairly represent a great body of public opinion.
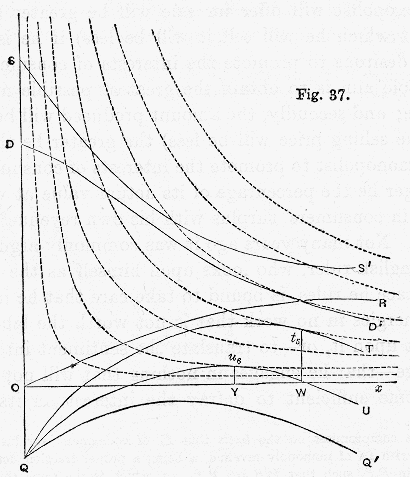 Fig. 37 may be taken to represent the case of a proposed Government undertaking in India. The supply curve is above the demand curve during its whole length, showing that the enterprise to which it refers is unremunerative, in the sense that whatever price the producers fix, they will lose money; their monopoly revenue will be a negative quantity. But
Fig. 37 may be taken to represent the case of a proposed Government undertaking in India. The supply curve is above the demand curve during its whole length, showing that the enterprise to which it refers is unremunerative, in the sense that whatever price the producers fix, they will lose money; their monopoly revenue will be a negative quantity. ButQT the total benefit curve rises above
Ox; and touches a constant revenue curve in
t5. If then they offer for sale an amount
OW (or, which is the same thing, fix the price at the demand price for
OW), the resultant consumers’ surplus, if taken at its full value, will outweigh the loss on working by an amount represented by
OW ×
Wt5. But suppose that, in order to make up the deficiency, Government must levy taxes, and that taking account of all indirect expenses and other evils, these cost the public twice what they bring in to the Government, it will then be necessary to count two rupees of the consumers’ surplus as compensating for a Government outlay of only one rupee; and in order to represent the net gain of the undertaking on this supposition, we must draw the compromise benefit curve
QU as in
fig. 36, but putting
n = ½. Thus
MP6 =
MP3 + ½
MP4. (Another way of putting the same thing is to say that
QU is drawn midway between the monopoly revenue (negative) curve
QQ‘ and the total benefit curve
QT.)
QU so drawn in fig. 37 touches a constant revenue curve in
u6, showing that if the amount
OY is offered for sale, or, which is the same thing, if the price is fixed at the demand price for
OY, there will result a net gain to India represented by
OY ×
Yu6.
Recherches sur les principes mathématiques des Richesses, Ch. IX. p. 113. Here, as elsewhere, he opened up new ground, but overlooked some of its most obvious features. Prof. H. L. Moore (
Quarterly Journal of Economics, Feb. 1906), basing himself partly on the work of Bertrand and Prof. Edgeworth, lays down clearly the assumptions which are appropriate to monopoly problems.
Industry and Trade is occupied with a study of problems akin to those which have been sketched in this chapter.
