The Economics of Welfare
By Arthur C. Pigou
WHEN a man sets out upon any course of inquiry, the object of his search may be either light or fruit—either knowledge for its own sake or knowledge for the sake of good things to which it leads. In various fields of study these two ideals play parts of varying importance. In the appeal made to our interest by nearly all the great modern sciences some stress is laid both upon the light-bearing and upon the fruit-bearing quality, but the proportions of the blend are different in different sciences. At one end of the scale stands the most general science of all, metaphysics, the science of reality. Of the student of that science it is, indeed, true that “he yet may bring some worthy thing for waiting souls to see”; but it must be light alone, it can hardly be fruit that he brings. Most nearly akin to the metaphysician is the student of the ultimate problems of physics. The corpuscular theory of matter is, hitherto, a bearer of light alone. Here, however, the other aspect is present in promise; for speculations about the structure of the atom may lead one day to the discovery of practical means for dissociating matter and for rendering available to human use the overwhelming resources of intra-atomic energy. In the science of biology the fruit-bearing aspect is more prominent. Recent studies upon heredity have, indeed, the highest theoretical interest; but no one can reflect upon that without at the same time reflecting upon the striking practical results to which they have already led in the culture of wheat, and upon the far-reaching, if hesitating, promise that they are beginning to offer for the better culture of mankind. In the sciences whose subject-matter is man as an individual there is the same variation of blending as in the natural sciences proper. In psychology the theoretic interest is dominant—particularly on that side of it which gives data to metaphysics; but psychology is also valued in some measure as a basis for the practical art of education. In human physiology, on the other hand, the theoretic interest, though present, is subordinate, and the science has long been valued mainly as a basis for the art of medicine. Last of all we come to those sciences that deal, not with individual men, but with groups of men; that body of infant sciences which some writers call sociology. Light on the laws that lie behind development in history, even light upon particular facts, has, in the opinion of many, high value for its own sake. But there will, I think, be general agreement that in the sciences of human society, be their appeal as bearers of light never so high, it is the promise of fruit and not of light that chiefly merits our regard. There is a celebrated, if somewhat too strenuous, passage in Macaulay’s Essay on History: “No past event has any intrinsic importance. The knowledge of it is valuable, only as it leads us to form just calculations with regard to the future. A history which does not serve this purpose, though it may be filled with battles, treaties and commotions, is as useless as the series of turnpike tickets collected by Sir Matthew Mite.” That paradox is partly true. If it were not for the hope that a scientific study of men’s social actions may lead, not necessarily directly or immediately, but at some time and in some way, to practical results in social improvement, not a few students of these actions would regard the time devoted to their study as time misspent. That is true of all social sciences, but especially true of economics. For economics “is a study of mankind in the ordinary business of life”; and it is not in the ordinary business of life that mankind is most interesting or inspiring. One who desired knowledge of man apart from the fruits of knowledge would seek it in the history of religious enthusiasm, of martyrdom, or of love; he would not seek it in the market-place. When we elect to watch the play of human motives that are ordinary—that are sometimes mean and dismal and ignoble—our impulse is not the philosopher’s impulse, knowledge for the sake of knowledge, but rather the physiologist’s, knowledge for the healing that knowledge may help to bring. Wonder, Carlyle declared, is the beginning of philosophy. It is not wonder, but rather the social enthusiasm which revolts from the sordidness of mean streets and the joylessness of withered lives, that is the beginning of economic science. Here, if in no other field, Comte’s great phrase holds good: “It is for the heart to suggest our problems; it is for the intellect to solve them…. The only position for which the intellect is primarily adapted is to be the servant of the social sympathies.”… [From the text]
First Pub. Date
1920
Publisher
London: Macmillan and Co.
Pub. Date
1932
Comments
4th edition.
Copyright
The text of this edition is copyright © 1932. This book is available through Transaction Publishers, Inc. Direct all requests for permissions and copyrights to Transaction Publishers, Inc.
- Preface to the Third Edition
- Note to the Fourth Edition
- Part I, Chapter 1
- Part I, Chapter 2
- Part I, Chapter 3
- Part I, Chapter 4
- Part I, Chapter 5
- Part I, Chapter 6
- Part I, Chapter 7
- Part I, Chapter 8
- Part I, Chapter 9
- Part I, Chapter 10
- Part I, Chapter 11
- Part II, Chapter 1
- Part II, Chapter 2
- Part II, Chapter 3
- Part II, Chapter 4
- Part II, Chapter 5
- Part II, Chapter 6
- Part II, Chapter 7
- Part II, Chapter 8
- Part II, Chapter 9
- Part II, Chapter 10
- Part II, Chapter 11
- Part II, Chapter 12
- Part II, Chapter 13
- Part II, Chapter 14
- Part II, Chapter 15
- Part II, Chapter 16
- Part II, Chapter 17
- Part II, Chapter 18
- Part II, Chapter 19
- Part II, Chapter 20
- Part II, Chapter 21
- Part II, Chapter 22
- Part III, Chapter 1
- Part III, Chapter 2
- Part III, Chapter 3
- Part III, Chapter 4
- Part III, Chapter 5
- Part III, Chapter 6
- Part III, Chapter 7
- Part III, Chapter 8
- Part III, Chapter 9
- Part III, Chapter 10
- Part III, Chapter 11
- Part III, Chapter 12
- Part III, Chapter 13
- Part III, Chapter 14
- Part III, Chapter 15
- Part III, Chapter 16
- Part III, Chapter 17
- Part III, Chapter 18
- Part III, Chapter 19
- Part III, Chapter 20
- Part IV, Chapter 1
- Part IV, Chapter 2
- Part IV, Chapter 3
- Part IV, Chapter 4
- Part IV, Chapter 5
- Part IV, Chapter 6
- Part IV, Chapter 7
- Part IV, Chapter 8
- Part IV, Chapter 9
- Part IV, Chapter 10
- Part IV, Chapter 11
- Part IV, Chapter 12
- Part IV, Chapter 13
- Appendix I
- Appendix II
- Appendix III
APPENDIX II
THE MEASUREMENT OF ELASTICITIES OF DEMAND
§ 1. WITH the information at present available it is not possible to lay down any propositions about the elasticity of demand for different commodities beyond those general propositions that are set out in Part II. Chapter XIV. As has been pointed out by Marshall,
*46 attempts to determine the elasticity of demand for any commodity in any market by a direct comparison of the prices and the quantities consumed at different times are exposed to very great difficulties. If it could be presumed that the reactions exercised by price-changes upon quantity demanded came about immediately, if the association of actual price-changes with people’s expectation of connected future price-changes in the same or the opposite direction could be eliminated, and if allowance could be made for those upward and downward shiftings of demand schedules, for which movements of confidence and alterations in the supply of monetary purchasing power are responsible, a comparison of the percentage changes of price between successive years with the percentage changes in consumption between the same years might, for commodities about which adequate statistics exist, yield a rough numerical measure of elasticity for amounts of consumption in the neighbourhood of the average actual consumption.
*47 It seems that for certain commodities the above presumption can reasonably be made. On the basis of it Professor Lehfeldt calculated, immediately before
the war, that the elasticity of the aggregate demand for wheat in the United Kingdom was about -0.6.
*48 But there is little hope that many elasticities will lend themselves to calculation in this direct way. It is, therefore, important to inquire whether any indirect method of calculation is available for overcoming difficulties due to the slowness with which reactions work themselves out.
*49
§ 2. Some years ago I devised a method, the basis of which is a comparison of the amounts of a commodity consumed by persons of different incomes at a given price, instead of a comparison of the amounts consumed by persons of given incomes at different prices.
Statistical data needed for this method are found in family budgets. Considerable attention has been paid both by State Departments and by private persons to the study of these budgets; and a number of tables have been printed to show the proportion of their income which families in different income groups expend upon the various principal sorts of commodities. It is possible so to manipulate these data as to derive from them information about certain elasticities of demand.
§ 3. Let us suppose that the data are better than they are, and that our tables give the expenditure of the group of workpeople whose wages lie between 30s. and 31s., of the group whose wages lie between 31s. and 32s., and so on continually for all wage levels. With this close grouping we may fairly assume that the tastes and temperament of the people in any two adjacent groups are approximately the same. That is to say, the desire for the
xth unit of any commodity (or group of commodities), the demand for which is not markedly correlated with the demand for other commodities, is equal for typical men in the 30s. to 31s. group and in the 31s. to 32s. group. Let the quantity of desire for the
xth unit of the commodity be φ(
x): or, in other words,
y being the desire for the
xth unit, let the desire curve for the commodity be represented by
y = φ(
x). We are entitled to assume further, in the absence of special knowledge as to the existence of correlation, that the desire curve of both groups for the commodity is independent of the quantity of other commodities consumed and, therefore, of the marginal desiredness of money. Let this marginal desiredness to the lower and higher income groups respectively be
µ1 and
µ2, and the quantities of the commodity consumed by these groups
x1 and
x2. Then, since the price paid for the commodity must be the same for both groups, we know that this price
p is equal both to
 and to
and to
 . These two expressions are, therefore, equal to one another. But, if, as it is reasonable to suppose when the incomes of the two groups are close together,
. These two expressions are, therefore, equal to one another. But, if, as it is reasonable to suppose when the incomes of the two groups are close together,
x2 differs only slightly from
x1, φ(
x2) may in general be written φ(
x1) + (
x2—
x1)φ'(
x1);
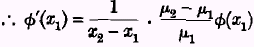
But the elasticity of the desire curve in respect of any consumption
x1 is known to be equal to
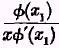 . Let this elasticity be written η
. Let this elasticity be written η
x1. It follows that
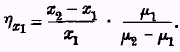
But, since a small change in the consumption of any ordinary commodity, on which a small proportion of a man’s total income is spent, cannot involve any appreciable change in the marginal desiredness of money to him,
*50 the elasticity of the desire curve in respect of any consumption
x1 is equal to the elasticity of the demand curve in respect of that consumption. Therefore the elasticity of demand, as well as the elasticity of desire, of the lower income group, in respect of its consumption of
x1 units, may be represented by η
x1, when:
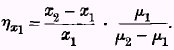 .
.§ 4. If we knew the relative values of
µ1 and
µ2, this equation would enable us to determine the elasticity of demand of the lowest income group for any commodity, the demand for which is not markedly correlated with the demand for other commodities, in respect of such quantity of the commodity as that group is consuming. Similar equations would enable us to determine the corresponding elasticities of each of the other income groups. If it is objected that our result would in practice be impaired by the fact that the higher income groups are apt to consume a better quality of commodity, and not merely a greater quantity, than the lower income groups, the difficulty is easily overcome by substituting in our formula for the quantities of the commodity that are consumed by the different groups figures representing their
aggregate expenditures upon it. This device escapes the suggested objection by treating improved quality as another form of increased quantity. In order to obtain the elasticity of demand for the commodity as a whole, it would be necessary to calculate the separate elasticities for all income groups and to combine them on the basis of the quantity of purchases to which they respectively refer.
§ 5. Unfortunately we do not know, and cannot ascertain, the relative values of
µ1 and
µ2. Consequently we are estopped from using the above analysis to determine the elasticity of the demand for any commodity in absolute terms.
*51 But this does not block
our investigation. For, by the process indicated above, the elasticities of demand in any income group can be determined, for all the things consumed in that income group, in expressions into which
µ1 and
µ2 enter in exactly the same way, namely, as the term
 . If, then, the several elasticities be η
. If, then, the several elasticities be η
x, η
y, η
z, and so on, any one of them can be expressed in terms of any other without reference to
µ1 and
µ2. These unknowns are eliminated, and we obtain the formula
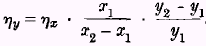
This result, it should be observed, only follows directly from the preceding argument, provided that the commodities concerned are both such that only a small part of a typical man’s income is normally spent upon them. In general, however, though the absolute formula for elasticities, from which the result is derived, is only valid on this assumption, the above comparative formula is approximately valid also for two commodities on which a large part of a typical man’s income is spent, so long as the part spent on the one does not differ greatly from that spent on the other. The reason for this is that the errors in the two formulae for absolute elasticities, which have to be combined, will tend to balance one another. Our comparative formula is seriously suspect only when it is used to obtain the relative elasticities of the demands of a group for two things, on one of which that group spends a large proportion, and on the other a small proportion, of its income. Apart from this, the formula, when applied to the statistics of quantities of, or expenditures upon, different commodities by neighbouring income groups, enables us to determine numerically the ratio of the elasticity of demand of any income group for any
one commodity (in respect of the quantity of the commodity actually consumed by it) to the elasticity of demand of the group for any other commodity. This information will often be valuable in itself. It is important to know whether the demand of workers with 35s. a week for clothes is about twice, or about ten times, as elastic as their demand for food. But the information is also valuable indirectly. For, if we can in some other way—through the examination of shopkeepers’ books or otherwise—determine the elasticity of demand of any income group, or collection of income groups, for one thing, we have here a bridge along which we may proceed to determine the elasticity of their demand for all other things.
§ 6. In explaining the above method I have, as indicated at the outset, assumed that our data are better than they are. This, I think, is legitimate, because there is no reason in the nature of things why these data should not be improved; and, indeed, there is little doubt that they will be improved. Even then, of course, any one attempting a detailed application of the method is certain to encounter serious difficulties, among which, perhaps, not the least will be that of deciding how far to treat different commodities separately and how far to group them together according to the purpose which they jointly serve. When put to the test, these difficulties may, no doubt, in some applications, prove insurmountable. From the results of an experiment made upon figures given in the second Fiscal Blue-book (pp. 215 and 217), I am, however, tempted to hope for better things. The figures refer to the expenditure upon “food” and “clothing” of groups of workpeople whose wages were respectively under 20s., between 20s. and 25s., between 25s. and 30s., between 30s. and 35s., and between 35s. and 40s. My method gave the ratio of the elasticity of demand for clothes to that for food for the several groups as follows:
| Workmen under 20s…. | 1.16 |
| From 20s. to 25s…. | 1.31 |
| From 25s. to 30s…. | 1.62 |
| From 30s. to 35s…. | 1.25 |
| From 35s. to 40s…. | 2.46 |
Apart from the drop in the ratio for workpeople earning from 30s. to 35s.—and it may be remarked in passing that the instances from which the average in this group is made up are only half as numerous as those in the two adjacent groups—these figures are continuous and in no wise incompatible with what we should expect from general observation. It is natural that among the very poor the demand for clothes should be nearly as inelastic
as the demand for food, and that, as we proceed to groups of greater wealth, its relative elasticity should grow. This small experiment, therefore, is not discouraging, and it is much to be desired that some economist should undertake a more extended study along similar lines.
*52
et seq.
Economic Cycles (chapters iv. and v.), makes calculations of the “elasticity” of demand for certain commodities without resort to the allowances stipulated for in the text. But, as he himself fully recognises, the elasticity, which his method enables him to measure, is not the same thing as, and is not, in general, equal to, the elasticity of demand as defined by Marshall and employed here. Marshall’s elasticity, if known, would make it possible to predict how far the introduction of a new cause modifying supply in a given manner would
affect prices; Professor Moore’s to predict with what price-changes changes in supply coming about naturally, in company with such various other changes as have hitherto been found to accompany them, are likely to be
associated. That this distinction is of great practical importance is shown by the fact that, whereas the elasticity of the demand for pig-iron, in Marshall’s sense, is, of course, negative—that is to say, an increase in supply involves a fall in price—the elasticity in Professor Moore’s sense, as calculated from his statistics, is positive. The reason for this is that the principal changes in the price of pig-iron that have in fact occurred are mainly caused by expansions of demand (general uplifts in the demand schedule), and not by changes in supply taking place while the demand schedule is unaltered. In certain conditions it might be possible to
derive Marshall’s elasticity from Professor Moore’s elasticity, provided that the reactions exercised by supply changes upon prices could be presumed to take place very rapidly. Apart from this presumption derivation would be impossible, however ample the statistical material.
et seq.
p per cent, and that this rise is the direct and sole cause of a fall in consumption of
a per cent. We cannot infer that the elasticity of demand either for consumption A or for consumption
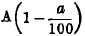 is equal to
is equal to unless
unlessp is small—strictly unless it is infinitesimal. If
p is not small, some assumption as to the relation of neighbouring elasticities must be made before any inference can be drawn. One possible assumption is that the demand curve is a straight line. On this assumption the elasticity of demand in respect of consumption A will be
 : and in respect of consumption
: and in respect of consumption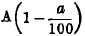 it will be
it will be . Another possible assumption is that the elasticity of demand is constant for all amounts of consumption from A to
. Another possible assumption is that the elasticity of demand is constant for all amounts of consumption from A to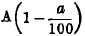 . On this assumption it can be proved, as Dr. H. Dalton has pointed out to me, that the said elasticity is not
. On this assumption it can be proved, as Dr. H. Dalton has pointed out to me, that the said elasticity is not but
but
This must lie between
 and
and
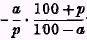 : and is probably not far from
: and is probably not far from

some alteration in the marginal desiredness of money, unless the demand for the commodity in question has an elasticity equal to unity. If the elasticity is anything other than this, a change in the consumption of the commodity will be accompanied by a transference of money from expenditure upon it to expenditure upon other things, or
vice versa. This must affect the marginal desiredness of money spent on these things, and its marginal desiredness, if affected in one field, is, since it must be the same in all, affected in all.
L’ elasticità dei consumi, suggests that the method described above can be extended to yield an absolute measure of elasticity by reference to the distinction between nominal and real prices. The money price paid by the higher income group is the same as that paid by the lower income group. But the real price is, he holds, less than this, in the proportion in which the income of the higher income group exceeds that of the lower. Thus, if the higher income group has 10 per cent more income, an equal money price paid by it implies a real price 10/11ths as great; and the elasticity of demand is obtained by dividing a virtual price difference of 1/11th into whatever fraction represents the associated consumption difference (
loc. cit. p. 22). This procedure is, however, illegitimate, because, on the assumptions taken, the virtual price of
all commodities to the higher income group is 10/11ths of what it is to the lower income group. Consequently, the difference in the consumption of
any particular commodity is not due solely to the difference in price of that commodity, and cannot, therefore, in general, be inserted in the formula for elasticity of demand. Professor Vinci has, in fact, tacitly assumed that the marginal desiredness of money is equal for the two groups—an assumption which would only be warranted if the demand of both for the sum of commodities other than the particular one under investigation had an elasticity equal to unity.
Economic Journal of December 1910.
Appendix III
