“How much do students learn in school?” The question is harder than it seems. You get one answer if you measure their knowledge at the end of the school year or right before graduation. You’ll probably get a very different answer, however, if you measure their knowledge a year, five years, or twenty years after graduation.
The latter measure is clearly more important. What good is “knowledge” that melts in your mouth like cotton candy? As you’d expect, however, we rarely measure long-term learning. Instead, we look for our keys under the streetlight because it’s brighter there. Our obsession with student achievement ends with graduation.
Fortunately, there are a few noble exceptions. My favorite: Bahrick and Hall’s “Lifetime Maintenance of High School Mathematics Content” (Journal of Experimental Psychology, 1991). The authors assembled a large sample of current students and adults (ages 19-84). They collected detailed information on their mathematics coursework, IQ, and other variables. And they reached some remarkable discoveries.
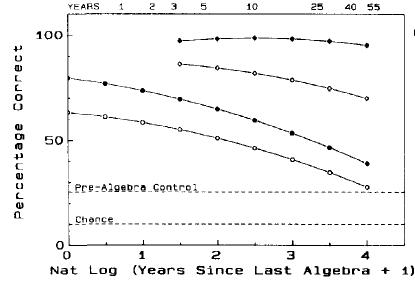
Here’s how knowledge of algebra decays over a lifetime. The lines (top to bottom) show the fitted scores for (1) people who studied more than calculus, (2) people who studied calculus, (3) people who didn’t study calculus but took another algebra course, and (4) people who didn’t study calculus and only took one algebra course.

If you’re a cheerleader for education, you’ll fix your gaze on the top two lines. People who go beyond calculus don’t just master algebra; they know algebra almost perfectly for the rest of their lives. People who stop with calculus do almost as well, their average score slowly declining from 90% to 75% over the course of fifty years. Wow!
If you’re someone like me, however, you’ll fix your gaze on the bottom two lines. After all, most students never take calculus. What benefit does this vast majority get out of higher mathematics? Not only is their proficiency low, but it decays fairly rapidly. Ten years roughly halves their edge over pre-algebra controls.
Non-economists will probably interpret this as an argument for making everyone take calculus. But what about the cost? Does it really make sense to torture everyone with four years of advanced mathematics to ensure that they don’t forget their first year?
Before you answer, consider one more finding from the paper. Bahrick and Hall constructed a measure of how much subjects “rehearsed” – i.e., used – algebra in their daily lives:
Those who reported no rehearsals were assigned zero on the scale; those who reported only activities or occupations of low or intermediate relevance were assigned a 1; those who reported highly relevant activities were assigned a 2 if they engaged in these activities 5 or fewer hours per year, a 3 for 6 to 100 hours per year, and a 4 for more than 100 hours per year. Those whose profession involved the continuous performance of highly relevant activities were assigned a 5.
Survey says:
The vast majority of subjects rarely use algebra no matter how proficient they are. Look at the fractions with rehearsal scores of 0 or 1: 89% for people who studied less than calculus, 91% for people who studied calculus, and 70% for people who studied more than calculus. If the students who already take calculus don’t use it in real life, why on earth should we push weaker students to match their achievement?
P.S. Today, October 17, GMU will be hosting a “flash debate” on government support for higher education between me and Pulitzer-prize winner Steve Pearlstein. The time: 1:30 PM. The place: GMU Fairfax campus, North Plaza, by the big clock tower.

READER COMMENTS
Daniel R. Grayson
Oct 16 2012 at 10:09pm
Hmm, it may not be that taking calculus solidifies your knowlege of algebra, but that mastering algebra enables and encourages you to take calculus. Or there’s a third factor that causes both.
secret asian man
Oct 16 2012 at 10:24pm
Learning calculus is not what teaches algebra.
Those who are capable of remembering algebra are also capable of learning calculus.
Those who are not capable of remembering algebra are incapable of learning calculus.
Thus, completion of a calculus class is merely a filter for ability. If you were to hold IQ constant, there would likely be only a very low correlation between calculus completion and algebra retention.
Kevin Dick
Oct 16 2012 at 10:25pm
@Daniel. Here’s an obvious common factor. People who like math take calculus. People who like math remember algebra.
Cameron Mulder
Oct 16 2012 at 11:10pm
I have always though we should move towards teaching more statistics and probability in high school.
Is there a more recent research on this? I get the impression that math is more critical to jobs today.
Scott Murphy
Oct 16 2012 at 11:20pm
This is Bryan’s attempt at bringing more communications and journalism majors into the fold.
steven
Oct 17 2012 at 1:03am
Cameron says teach more statistics in school…
I took statistics in college. I cannot remember anything about that course even though I did well in it. It was much more forgetable than algebra.
Jehu
Oct 17 2012 at 1:37am
The act of taking Calculus, and the differential equations classes post-Calculus gives you a tremendous amount of experience and reinforcement in your algebra skills. A lot of students only REALLY master Algebra by the time they take Calculus and only actually master Calculus by taking the various differential equations courses. By master, I mean that a reasonable fraction of the knowledge of that lower level of mathematics becomes available to the gut.
Algebra, in particular, available to your gut is tremendously useful, and not just for engineers, scientists, or the like. Questions like, where should I shop for my typical basket of groceries, given costs for visiting multiple stores, are very good exercise for one’s mathematical ‘gut’.
Your gut will also tell you frequently when something with a mathematical underpinning just LOOKS wrong.
Ken P
Oct 17 2012 at 1:53am
This ignores the problem solving capability that comes with math education as well as the ability to see the world mathematically in general.
Tracy W
Oct 17 2012 at 7:02am
In NZ, at least when I went through, nearly everyone started learning calculus at age 15 (if you were very poor at maths you could take Math With Applications instead, or as we called it, veggie-math, which was things like reading timetables).
And interestingly, note that in your table over a quarter of people who never took calculus make up the bulk of those using it. I wonder how many of those are skilled tradespeople?
Jack
Oct 17 2012 at 8:05am
Prof. Caplan: You are right, but most people (educators, parents, politicians) find tracking distasteful. We don’t want “smart-kid” and “dumb-kid” tracks. Hence the one-size-fits-all algebra class.
I think at least 50 percent of kids could do well without high school algebra. But it is seen as elitist to suggest different tracks.
Scott Wentland
Oct 17 2012 at 8:26am
@Caplan
I am curious, what do you think about the proposed homework ban in France?
Brandon Berg
Oct 17 2012 at 8:45am
As Jehu says, there’s definitely a causal mechanism at play. Calculus involves application and practice of algebra, and these improve retention and deepen understanding. Likewise, I got a 5 on the AP Calculus BC test, but I was just memorizing formulas. It wasn’t until I took electromagnetic physics in college that I really understood integral calculus. If I hadn’t, I probably would have almost completely forgotten calculus by now.
That said, Bryan’s right. I never use this stuff as a software engineer (though I might in certain types of software engineering, such as game programming, simulations, or financial programming). Ironically, the one job where I did use it was a college job selling vinyl siding–they needed a projection of cost savings customers might expect over different time periods. In retrospect, I probably should just have used Excel.
Brandon Berg
Oct 17 2012 at 8:48am
By the way, Bryan, with all the things you want to cut from the standard high school curriculum, what exactly do you want to keep, or add in replacement? Or do you think that secondary education in general fails cost-benefit analysis for most students?
Francis
Oct 17 2012 at 8:48am
There is also the general moral argument against forcing people to study things (or to pretend to study them).
Brandon Berg
Oct 17 2012 at 8:51am
Jack:
My high school (late ’90s) had four tracks for most academic subjects. Is that no longer the norm? Was it not the norm then?
Jeff
Oct 17 2012 at 8:58am
How many people who only took algebra would even be able to determine if they are using algebra on a daily basis? The woman next to me is the type that agrees with Barbie (“Math is hard!”), and would doubtless say she never uses algebra, but that is just because she associates algebra with x’s and y’s, not everyday decisions like how figuring out how much gas she can get for $40. Basically, I’d be more sceptical than Bryan about what Table 2 tells us.
Alan Cole
Oct 17 2012 at 10:06am
I don’t believe 14-year-olds have particularly valuable time. They might as well spend some of it accumulating human capital.
egd
Oct 17 2012 at 10:52am
“Does it really make sense to torture everyone with four years of advanced mathematics to ensure that they don’t forget their first year?”
More importantly: can we reasonably expect people who take four years of calculus to remember their first year of algebera?
I suspect “algebera retention” is self selecting. This is born out in the table: people just starting out in calculus (3 years since algebera) have a higher algebra retention than those not taking calculus. Interestingly, people just starting out in post-calc. (3 years since algebera) have a higher algebra retention than those not taking higher math.
I think it would be informative to know when the students took algebera and when they took calculus, or post-calculus courses.
Finch
Oct 17 2012 at 10:53am
Related article in the Boston Globe:
http://www.boston.com/news/nation/2012/10/11/report-links-earning-power-college-degree-engineers-top-list/JY9ft22NbkppcgoFOHhPYK/story.html
Based on these census reports:
http://www.census.gov/prod/2012pubs/acsbr11-04.pdf
and
http://www.census.gov/prod/2012pubs/acsbr11-10.pdf
Cliffs: (1) Let your children grow up to be engineers, and (2) the idea that less technical fields will let them earn more later in life is a myth.
My attempt at interpretation: The more numerate your profession, the more you will earn over your life. The key question for Bryan’s algebra data is whether we are making children more numerate, or discovering which children are more numerate.
Michael D
Oct 17 2012 at 11:14am
I agree with Brandon and Jehu. I’ve been learning math my whole life, got an undergraduate degree in math and am now working in a math related field and their assessments mirror my own experiences.
I did well in Algebra in middle school, but I didn’t really have a deep understanding of it until high school when we began doing pre-calc and trig, both of which require applying Algebraic concepts.
Similarly, I did well in Calculus in high school, but I didn’t have anywhere near the deep understanding I have now until I took higher level math classes in college that required applying Calculus concepts.
I am pretty confident in saying that I will retain most of the algebra and calculus knowledge I have now for the rest of my life. If I hadn’t spent the last ~6 years practicing and reinforcing these skills that would definitely not be the case. The point Bryan seems to be trying to make here is that forcing everyone to take 1 year of college is wasteful and pointless, and I agree with him.
MG
Oct 17 2012 at 11:48am
@Scott Wentland
Thanks for that gem of a link. Whenever I calm myself into thinking that “Harrison Bergeron” was just a work of fiction…
Hopaulius
Oct 17 2012 at 12:12pm
The purpose of a general education is to train children/youth in a range of skills that they may or may not “use” later in life. For better or worse, American youth are immature. They don’t know yet what is going to ignite their passion later in life. If they do not learn math skills such as algebra while they are young, they will find it nearly impossible to catch up later. I got as far as one calculus course in high school, but my memory of it is zero, and algebra is hazy. But I remember the precise moment when my passion for math died. My geometry teacher had claimed that a point on a wheel rolling on a surface would make a loop. This seemed intuitively wrong to me, since no part of the wheel was reversing direction. So I set out to construct a proof. I presented it to the teacher, who looked at it for a moment, and then said, “I don’t understand this” and handed it back to me. Who knows? If that teacher had taken my attempt seriously and pointed out its flaws or praised its success, my passion for math might have grown into a career. Instead, it withered.
jseliger
Oct 17 2012 at 12:50pm
The vast majority of subjects rarely use algebra no matter how proficient they are.
On the other hand, those who do use algebra may be doing very important things for society as a whole—and the economy—like writing the software that I’m using to post this comment.
We probably can’t predict in advance who these people are likely to be, so we teach everybody, even if we’re only hoping to reach them.
Maximum Liberty
Oct 17 2012 at 1:16pm
@secret asian man:
While you might be right about ability, I would have said:
Max
Hana
Oct 17 2012 at 1:37pm
I am surprised by the table illustrating use of algebra. On a daily basis most people make decisions requiring elementary algebra.
I want to go to a movie with my spouse. The movie tickets are $12.00 each. A baby sitter will cost $4.00 an hour for 3 hours. We want one large popcorn at $7.00, one Milk Duds for $3.00, and two sodas for $3.50 each. I have $60. Do I need to stop at the ATM before we go to the movie?
Whether it is planning a party, working at your job, scheduling your day, purchasing groceries, or cooking a meal, people handle algebraic problems all of the time. The relative ease that we have in accomplishing those calculations does not mean that we don’t do them. It seems the problem is people’s understanding of the survey question, not the use of algebra.
Bostonian
Oct 17 2012 at 2:47pm
People faced with the problem described by Hana may do it in their heads or write an expression such as
12*2 + 4*3 + 7 + 3 + 2*3.5
on a piece of paper and compute the result. They probably regard it as an arithmetic problem. I wonder if taking an algebra course helps people solve such arithmetic problems. I doubt that even 10% of the population knows and uses basic algebra formulas, such as a^2 – b^2 = (a+b)*(a-b) to solve problems in their daily lives or at work.
It is not politically correct to give IQ tests to filter out job candidates, because this has a “disparate impact”. Filtering using a college degree that required some algebra serves a similar purpose and is more politically palatable. Math instruction and testing may serve as a quasi-IQ test.
Methinks
Oct 17 2012 at 3:20pm
I agree with the commenters who point out that our understanding of algebra deepens when we move on to calculus. In fact, I found that I understood the previous level of math much better when I took the subsequent level (and there’s a difference between being able to do well on a test and REALLY understanding something).
I do wish that basic statistics were taught in high school. We are sorely lacking in basic understanding of statistics.
Bostonian,
I think you’re right that hana’s is an arithmetic problem, but upthread someone pointed out a daily basic algebra problem: figuring out how many gallons of gas you can buy for $40.
I don’t think that an IQ test is going to tell you what you think it will. I’ve interviewed a lot of candidates in my life and, in my experience, you can determine pretty quickly during the interview process if they’re intelligent or not. Whether or not they’ll be a good fit is a more difficult thing to determine in an interview. I have found that a lot of people who have taken a lot of math classes are just not as brilliant as I’d hoped they would be.
MingoV
Oct 17 2012 at 5:19pm
That may be the wrong question. Teaching algebra in school has more utility than providing sustained knowledge of algebra. Algebra is a conceptual leap from arithmetic, and it is vastly different from language skills. Students who learn algebra, even if they forget it a few years later, may still have gained something. They successfully used their brains in a different way, and that may give them confidence and help them accomplish other new and different mental tasks.
The college course that most closely correlated with success in medical school (in the 1980s and 1990s) was calculus (which is not used or needed in medical school). The ability to master calculus correlates with the ability to master complex aspects of medicine such as renal physiology, nervous system function, homeostatic systems, bone maintenance and metabolism, pharmacology, etc. I suspect that ability to master algebra has similar correlations with mastering other seemingly unrelated subjects.
Steve Sailer
Oct 17 2012 at 9:19pm
It’s not unreasonable to force everybody to try to get through Algebra I, since we’ll discover a few kids who are smarter than they thought they were that way.
But, there are big diminishing returns to demanding that everybody pass Algebra II to be a high school graduate, as the Gates Foundations has been trying to bribe and bully school districts into doing.
steven
Oct 17 2012 at 10:34pm
“I think you’re right that hana’s is an arithmetic problem, but upthread someone pointed out a daily basic algebra problem: figuring out how many gallons of gas you can buy for $40.”
This is a basic math problem. Not algebra.
Methinks
Oct 17 2012 at 10:56pm
Steven, don’t American schools call it “algebra” the minute variable equations are introduced?
Brad
Oct 17 2012 at 11:34pm
Shouldn’t we let the free market determine who receives mathematical training? If labor demands advanced training in math, and current supply cannot meet that demand, wages will respond accordingly. This will compel many folks, probably the ones who are more mathematically-inclined, to get more advanced training.
Portland math tutor
Oct 18 2012 at 1:34am
Why teach History? Geography?
Literature? Composition? Anything at all?
Education is not torture. It is a privilege that many have fught and died for. To act as though the teaching of abstract problem solving is tortorous or a waste of time is both short-sighted and silly. It is no wonder the U.S. is in decline in both education and economics.
Societies who value the power of education will surpass and absorb this one.
Bostonian
Oct 18 2012 at 8:18am
I would like to see a source for the interesting statement made by MingoV,
“The college course that most closely correlated with success in medical school (in the 1980s and 1990s) was calculus.”
Finch
Oct 18 2012 at 9:06am
> I would like to see a source for the interesting
> statement made by MingoV,
> “The college course that most closely correlated
> with success in medical school (in the 1980s and
> 1990s) was calculus.”
Assuming it’s true it’s consistent with both (1) calculus is just a great IQ test, so people who do well in calculus are smart and will do well in an arbitrary subject, and (2) learning calculus is an experience that makes you better at learning other things. Although I’m not familiar with the literature, Bryan often states that transferability of learning is weak at best and that that is well supported in the literature. So assuming MingoV an Bryan are correct, I’d bet on (1).
Arpan
Oct 18 2012 at 11:08am
Grr, I’d love to attend (or simply watch) that debate.
Brian B
Oct 18 2012 at 1:54pm
“If you’re someone like me, however, you’ll fix your gaze on the bottom two lines.”
Bryan,
Sounds like confirmation bias to me. What your post didn’t say, and should, is what the paper actually concluded. According to the abstract, the results shown in the first graph are for people “who performed equally well in the high school course!” Moreover, they found that indicators such as the SAT and grades had “trivial effects” on the performance decline. In other words, these results are NOT due to IQ or other measures of mathematical ability and not primarily selection effects.
What is going on, as alluded to above, is the strengthening of algebra knowledge through repeated transfer of skills to new contexts. As is true of any subject, lasting memory of the skill or information requires its integration into our conceptual schemes. This only happens when the concepts are used in diverse contexts.
The data, then, DO provide compelling evidence for the validity of calculus as a reinforcer of more basic math skills.
But should students bother learning it at all if they never use it? You suggest no, but I think you are overlooking the sizable opportunity costs in not learning basic skills (I would consider algebra to be a basic skill of abstract reasoning). People who are easily intimidated by the use of these mathematical skills simply avoid situations where they come up. Out of fear, not rational choice or preference, they restrict what they choose and how they behave. In the end, these self-restrictions are costly for everyone and represent a genuine threat to individual liberty.
MingoV
Oct 18 2012 at 5:35pm
Bostonian writes:
I don’t remember the source. It probably came from data collated by the Association of American Medical Colleges. Grades in calculus correlated with medical school grades better than grades in organic chemistry, mean grades in all science courses, overall college GPA, and MCAT scores. I doubt that the correlation still holds. Medical school education was revamped in the 1990s and early 2000s: it is less rigorous and has much less emphasis on basic sciences.
MingoV
Oct 18 2012 at 5:41pm
Finch wrote:
I don’t believe that is the answer, because IQ has too many components. Example: Alice and Brenda both have IQs of 125, but Alice struggles with calculus while Brenda easily aces it. I think that ability to master calculus correlates well with the aspects of intelligence needed to master complex medical sciences.
Hana
Oct 18 2012 at 7:13pm
The example I had given is elementary algebra. The variables are a=tickets, b=baby sitting, etc. For those without textbooks handy, go to wikipedia.
I repeat my assertion that people engage in algebra and even calculus all the time, while, admittedly, not being aware of it. Driving to SFO during rush hour or late night from my home covers the same distance. But, the variables change. We could plot the entire trip. A rush hour trip would have a much different graph obviously than the late night trip. (Part of the equation is the 5 minute long light on El Camino, and the 10 minutes to get onto 101, neither of which are part of the equation late night). The polynomial equations are of course different(I know this is not actually true, just that many values become zero when the trip is just a simple time distance problem), but the resultant first derivatives(the distance of the trip) are equal.
People use algebra and calculus, they are just perfectly content being blissfully unaware of it.
Methinks
Oct 18 2012 at 8:10pm
So, I was just over at Cafe Hayek, where I saw this brand new post by Don Boudreaux where he quotes from an Alvin Roth paper:
“The National Bioethics Advisory Commission (2001), writes that paying subjects to participate in medical experiments may be coercive. They go on to say that, if an institutional review board is concerned that the subjects in an experiment may be economically disadvantaged, it may require that the researchers reduce the payments they make to participants. The concern here is … to protect low-income participants from being faced with such a high participation fee that they would feel coerced to participate.”
Well, so much for math (which I’m assuming the members of the committee were pretty good at) weeding out the logic challenged.
Neeraj Krishnan
Oct 21 2012 at 3:35pm
What would you say about teaching Shakespeare? Or Keats? What percentage of people use Shakespeare or Keats in their daily lives? None? They should still be taught. We should teach fundamental/profound human achievements in all areas (mathematics, literature, natural sciences), its part of what makes humans civilized! Training people to be productive members of an industrial workforce is only part of the reason for education.
ajv
Oct 23 2012 at 8:11pm
High school algebra is very valuable to all students as a required course. Taking algebra in high school ensures that students have the necessary mathematics skill to perform at a competent level if they decide to enroll in college after graduation. College requires completion of at least 1 math course just as a liberal studies requirement however every major will have varying additional levels of mathematics as required courses. Preparing students with algebra in high school ensures that they will not be lost in these higher level courses and will not have to take remedial math courses in most cases. Even if ones grasp of algebra fades quickly with age it is a valuable skill to have learned and even if someone is reduced to just the basics it can be the difference between struggling to comprehend a simple math based task and instinctively being able to figure it out. Many subjects may not use mathematics often but grasping even the basics of algebra while in high school ensures that a student has at least had competent instruction in the subject. If algebra was not mandatory in high school many students would never even set foot in a math class unless they were forced to. Having it as both a mandatory course and in many cases as a graduation requirement ensures that every high school student should theoretically leave with a basic understanding of algebra that they can either use to pursue more math courses in the future or simply fall back on when the occasion requires it.
Tibor Mach
Oct 28 2012 at 10:28am
Well, I study maths at a university (finnishing my Ms degree in probability theory this year and hopefully continuing in a PhD programme) and I have quite a strong opinion (based on personal experience) on the question of the article.
My answer is definitely NO, it does NOT.
The way “mathematics” is taught at secondary schools is just abysmal. I am from the Czech republic, but from reading for example this essay by Lockhart plato.asu.edu/LockhartsLament.pdf I conclude the situation is in no way different e.g. in the US. By the way I reccomend that one to anyone who wants to know what mathematics is actually about and what is so wrong with the way it is taught. I will try to briefly summarize.
First of all, secondary schools “mathematics” is not mathematics at all. It is some sort of a twisted accountant’s dream. Mathematics is about being creative, about actual thinking and coming up with ideas of your own. This secondary school “mathematics” is quite the opposite. It mostly consists of teaching algorithms and “rules” how things are done without any insight and any deeper explanation, without the students having any chance to develop their own thoughts.
The facts secondary school “mathematics” can teach you are irrelevant for I would say 95 percent of the students. It is the process of thinking that matters, but sadly that is not really present at all. The result is not only a waste of time, but a developing misunderstanding of what mathematics is about and fewer people considering studing actual mathematics.
In the essay i mentioned, Lockhart says that it is quite possible that the most brilliant mathematician of our time may be a waitress in a motel in Arizona who always thought she sucked at maths. I could not agree more.
I myself had a 4 (in CZE primary and secondary schools there are marks from 1 to 5, 1 being excellent and 5 being unsatisfactory) from mathematics in the fourth year of my grammar school (after witch I changed the school) and this year I had a stipendium with straight A at what is considered the most difficult maths school in our country. My choice of that school however was rather accidental (I am really glad I did it though) and had I stayed at that grammar school, I would probably have not chosen it.
There are likely much better minds than my own who made the mistake (by little fault of their own) of confusing mathematics with what it is claimed to be at secondary schools and who did not go for what might be the best for them because of that.
All that said, I think the only solution to that problem is to get rid of the state in education. Apart from other benefits, it opens possibilities of alternative way of teaching mathematics (algebra being a part of it), or better yet of actually teaching mathematics and not accountancy painted as such.
sarenzalando
Oct 30 2012 at 5:20pm
Get into‘t test drive so difficult, the best points go in case you extremely are expecting it to.
sarenzalando http://www.soyoyoso.com/
Comments are closed.