The Calculus of Consent: Logical Foundations of Constitutional Democracy
By James M. Buchanan and Gordon Tullock
This is a book about the
political organization of a society of free men. Its methodology, its conceptual apparatus, and its analytics are derived, essentially, from the discipline that has as its subject the economic organization of such a society. Students and scholars in
politics will share with us an interest in the central problems under consideration. Their colleagues in
economics will share with us an interest in the construction of the argument. This work lies squarely along that mythical, and mystical, borderline between these two prodigal offsprings of political economy. [From the Preface]
First Pub. Date
1958
Publisher
Indianapolis, IN: Liberty Fund, Inc.
Pub. Date
1999
Comments
Foreword by Robert D. Tollison.
Copyright
The text of this edition is copyright: Foreword, coauthor note, and indexes ©:1999 by Liberty Fund, Inc. Content (including Preface) from The Calculus of Consent, by James M. Buchanan and Gordon Tullock, ©: 1962 by the University of Michigan. Published by the University of Michigan Press. Used with permission. Unauthorized reproduction of this publication is prohibited by Federal Law. Except as permitted under the Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a data base or retrieval system, without prior permission of the publisher. For more information, contact the University of Michigan Press: http://www.press.umich.edu. Picture of James M. Buchanan and Gordon Tullock: File photo detail, courtesy Liberty Fund, Inc.
- Foreword
- Ch. 1, Introduction
- Ch. 2, The Individualistic Postulate
- Ch. 3, Politics and the Economic Nexus
- Ch. 4, Individual Rationality in Social Choice
- Ch. 5, The Organization of Human Activity
- Ch. 6, A Generalized Economic Theory of Constitutions
- Ch. 7, The Rule of Unanimity
- Ch. 8, The Costs of Decision-Making
- Ch. 9, The Structure of the Models
- Ch. 10, Simple Majority Voting
- Ch. 11, Simple Majority Voting and the Theory of Games
- Ch. 12, Majority Rule, Game Theory, and Pareto Optimality
- Ch. 13, Pareto Optimality, External Costs, and Income Redistribution
- Ch. 14, The Range and Extent of Collective Action
- Ch. 15, Qualified Majority Voting Rules, Representation, and the Interdependence of Constitutional Variables
- Ch. 16, The Bicameral Legislature
- Ch. 17, The Orthodox Model of Majority Rule
- Ch. 18, Democratic Ethics and Economic Efficiency
- Ch. 19, Pressure Groups, Special Interests, and the Constitution
- Ch. 20, The Politics of the Good Society
- Appendix 1, Marginal Notes on Reading Political Philosophy
- Appendix 2, Theoretical Forerunners
 The Bicameral Legislature
The Bicameral Legislature
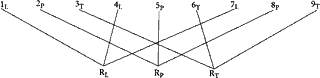
The two-house or bicameral legislative assembly is a common institution in Western democracies. This institution represents a particular configuration of the constitutional variables discussed in Chapter 15, and it may be analyzed, up to a point, in terms of our models. We shall proceed first to postulate an extreme case. Let us assume that a social group is composed of 9 persons, whom we shall designate by numbers 1 to 9. Further, we assume that these persons may be easily classified into three distinct interest or pressure groups, which, for convenience, we shall call: Labor, Property, and Trade. We shall use the subscripts L, P, and T to classify the numbered individuals.
Let us assume that the group has adopted a political constitution. All constitutional decisions have been made. (After analyzing the operation of the two-house system, we shall return to discuss the constitutional issue concerning the “efficiency” of this system.) The constitution calls for a bicameral legislature. There are to be three representatives in each house, and simple majority decision is required for action in each house. Final collective decision requires the approval of both houses.
Representatives to the first house, which we shall call the “House,” are to be elected on a functional basis. The three interests are each allowed to elect a single representative by simple majority vote. We may diagram the constituents of each representative to the House in the following way:
 |
In the second house of the legislature, which we shall call the “Senate,” the basis of representation is fully randomized, that is, each constituency includes within it each of the defined interest groups. We may diagram the constituents of each representative to this house as follows:
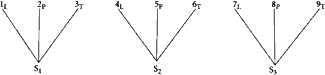 |
The question is that of determining how this two-house legislature will work in producing collective decisions. To carry decision, a majority of each house is required. The minimum effective coalition would be composed of four members, two from each house. Let us initially confine our attention to a single, isolated issue. Suppose that RL and RP form a majority in the House, and S1 and S2 form a majority in the Senate. Let us look carefully at the combined coalition: RL, RP, S1, S2. No difficulty arises when we consider the first two members. These representatives will try to further the interests of Labor and Property, which, for current purposes, we assume to be well-defined and homogeneous over individuals in the groups represented. The interests represented by S1 and S2, however, will depend on the effective voting coalitions that have been successful in local elections. In order for the two-house legislature to yield results similar in nature to the single-house legislature, both S1 and S2 must represent coalitions of Labor and Property interests. In specific terms, S1 must be elected by the coalition of 1L and 2P, and S2 must be elected by the coalition of 4L and 5P. Under these highly restricted conditions, collective action would tend to promote the interests of Labor and Property at the expense of Trade. This result is identical to that which would arise from the operation of a single legislative body operating under the same decision-making rules. To be generally true, however, this requires that a majority of the representatives in the randomized-basis house, the Senate, be elected by the same coalition of interests that forms the majority in the functional-basis House. This requirement would appear to be rarely met, especially as we move beyond the abstract models and consider a world in which interests are many, changing, and ill-defined.
Returning to the coalition RL, RP, S1, S2, now assume that either S1 or S2 should be elected by a majority that includes a voter from the Trade group. In this case no legislation could find majority support in both houses unless it was genuinely to the “general” interest of the whole social group. “Class” or “discriminatory” legislation, such as that which could be predicted to arise under the previously discussed configuration, is no longer possible. If, in order to pass both houses, the “representative” of each interest group must participate in an effective coalition, the two-house system introduces a qualified rule of unanimity into the collective-choice process.
It seems clear that the two-house system of representation introduces an element of uncertainty that was not present in our other models. Whereas we could not, in the analysis of a single group, predict the identity of the members of the winning and the losing coalitions in single issues, we were able to indicate the size of the minimum effective coalition that would be required to carry legislation. Moreover, from this limited amount of information some predictions could be made about the degree of minority exploitation and the degree of possible social waste. This is no longer possible under the two-house system, even when we continue to employ the same basic behavioral assumptions. As our examples have shown, the two-house legislature may produce results ranging from those equivalent to simple majority voting in a single house to those equivalent to the operation of the unanimity rule in a single house. The precise results will depend in each case on the overlapping of the interest-group coalitions in each house.
A few points seem worth noting. It is evident that the two-house system will involve considerably higher decision-making costs than the single-house system, given the same rules for choice under each alternative. From this it follows that, unless the two-house system is expected to produce some offsetting reduction in external costs, there is little reason for its rational support. Translated into more practical terms, this means that unless the bases for representation are significantly different in the two houses, there would seem to be little excuse for the two-house system. On the other hand, if the basis of representation can be made significantly different in the two houses, the institution of the bicameral legislature may prove to be an effective means of securing a substantial reduction in the expected external costs of collective action without incurring as much added decision-making costs as a more inclusive rule would involve in a single house. For example, to produce the same results in a single-house legislature, a rule of three-fourths majority might be required under certain circumstances. However, the decision-making costs involved in the operation of this majority might be significantly greater than those involved in the two-house legislature with each house acting on simple majority-voting principles. A priori, it does not seem possible to make such comparisons readily.
Vote-trading will, of course, take place in the two-house legislature, as we all must recognize. The process of vote-trading through logrolling becomes somewhat more complex and its analysis considerably more difficult. In order to undertake this analysis, let us consider briefly a group of 49 voters who have organized themselves in 7 constituencies of 7 voters each for the purpose of electing one house of a legislature, and in another set of 7 constituencies of 7 each for the purpose of electing the other. Let us suppose the constituencies consist, respectively, of the columns and rows of the following square (Figure 20).
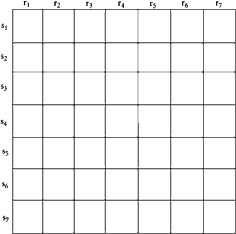 |
Figure 20 |
This is a system which follows the organizational principle which we may call “complete diversity.” Although complete diversity is unknown in political practice, it provides an excellent starting point for further analysis. The system, of course, is not limited to a group of 49 members. The 9-man electorate discussed above was also organized according to this rule, and a group that may be shown by a square of 199 by 199 will be used later in the chapter. Nor is it necessary that the illustrative diagram be a square; an oblong rectangle, with more representatives in one house than in the other, would be perfectly acceptable. Finally, our reasoning would not be changed if there were more than one voter reflected in each square of the diagram. Thus, we can consider a situation in which each square contains, say, 10,000 voters as one of complete diversity. The only requirement for complete diversity is that the members of the constituency of a representative in one house be distributed evenly among all of the constituencies for the other house.
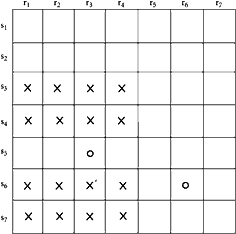 |
Figure 21 |
The smallest bargain which could enact a group of measures in this type of legislature would involve a coalition of 16 voters, arranged generally like the X’s in Figure 21. The coalition must include 4 voters in each of 4 constituencies of each legislative chamber. At first glance, it might appear that voting under a two-house legislative system leads to the same results as a one-house legislature, since this coalition is also that necessary to get a measure through a one-house legislature.*52 In fact, this coalition would get a measure through either of the two houses which are elected by the completely diverse electorates shown on our diagram. A little further consideration, however, indicates that this form of bargaining would not be feasible.
Suppose, for example, that voter X’ on the diagram decided that he was not being fairly treated and asked for a change which would lead to higher compensation for himself. The remaining members of the coalition would either have to give in or else construct a radically different bargain. If X’ were left out of the bargain, it would be necessary to drop either the row s6 or the column r3 and substitute another row or column for it. In other words, any member of such a coalition can be replaced only by radically changing the form of the coalition. In the mathematically convenient 199 by 199 square, a coalition of 10,000 voters organized like the X’s in Figure 21 could control the votes of both houses. However, if one member of the coalition demanded more compensation, then his coalition partners would have the choice of either giving in to his demands or of dropping him and 99 other members of the coalition. This situation is one in which substantial unanimity among a specified group is required to form the coalition, and the difficulties of getting unanimity in practice have been previously discussed. For each individual member of the coalition, investment of resources in strategic bargaining with the objective of getting much more than an equal share of the total returns from the coalition would be rational. In situations where large investments in strategic bargaining are rational, the cost of bargaining becomes prohibitively high. Thus we have an interesting situation in which, in essence, there are two costs-of-higgling functions. In addition to the decision-costs curve associated with changing voting rules, there is also a cost-of-higgling curve associated with the type of bargain to be struck. Although a minimum-membership bargain of the sort shown in Figure 21 would be the most economical from the standpoint of its members, the bargaining costs involved in making it up are prohibitive and this type of coalition can, therefore, be ruled out.
If X’ decides that he is not receiving favorable enough consideration from his coalition partners, they have yet another alternative to paying him what he asks or radically reconstructing the organization of the bargain. They could replace X’ by two other voters, who are located like the two O’s in Figure 21. A coalition constructed by this method, however, will be larger than one composed of people in the arrangement of the X’s and will also be composed of two classes of voters: those whose favorable consideration of the bargain is necessary to obtain approval in each one of both chambers, and those like the O’s whose vote is necessary only to obtain a majority in one or the other of the two chambers.
Leaving aside, for the time being, the question of the size of the new coalition, let us consider the bargaining problems raised by the existence of two classes of members of the coalition. There are two possible ways of dealing with the matter. Leaders may try to treat all members of the coalition equally, or they may choose to “compensate” the members of the two classes differently. The first leads to impossible difficulties. For example, if a policy were adopted of compensating the O’s equally with the X’s, then any X would know that the cost of replacing him would be two times the current “payment” received by the members of the coalition. It would only be rational for him to insist on receiving, say, 1.9 times the amount that others were receiving. If this offer were refused by the other members of the coalition, then they would have to obtain two replacements, and this is even more expensive than meeting his offer. Thus, each voter whose vote is required for approval of the measure in two houses would, if he were rational, hold out for about twice the standard “rate” of compensation. However, it is obviously impossible for a coalition to pay all of its members equally and at the same time pay some of them twice as much as others. The result would be that coalitions which attempted to stick to the system of making equal payments would find themselves, once again, confronted with members who invested sizable amounts in strategic bargaining, and the costs of bargaining would be too high for such a system to be feasible.
The contrary system of “paying” the members of the two classes differently does not raise this kind of problem. If each member of the coalition whose vote is necessary in both houses gets twice what a member whose vote is necessary in only one house does, then members of the coalition should get merely the marginal value of their votes. Any member withdrawing from the coalition can be replaced readily by one or two other voters, and there is, therefore, no incentive to invest excessive resources in strategic bargaining. However, if this two-category system is adopted, then there is no particular reason why coalition managers should favor voters whose votes are necessary in two houses, and who cost twice as much, over voters whose votes are necessary in only one house. The coalition can be made up just as “cheaply” from one type or from the other. This being so, there is no particular reason to expect that people trying to make up such a coalition will concentrate on voters who are necessary in both houses. Moreover, if they do not follow a conscious policy of trying to get such voters into the coalitions, then there would be only a random overlap between the voters in the coalitions which control the majority in each house.
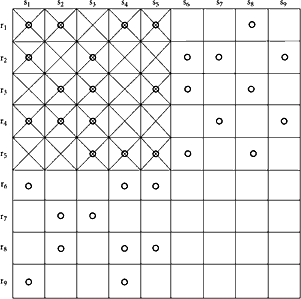 |
Figure 22 |
This may be illustrated in Figure 22. The crosshatched squares represent the minimum-sized coalition (5 by 5 in the 81-voter group with two houses of 9 constituencies each) that would be necessary to secure a majority in both houses. This coalition, however, would be no more likely to arise than that shown by the squares marked “O” if the support of the “less powerful” voters (those marked “O” which fall outside the 5 by 5 crosshatched matrix) can be secured at a lower bargaining “price” than the “more powerful” voters. This suggests that in the two-house system the minimum-sized coalition (in terms of numbers) need not arise, even on the assumption of fully rational behavior on the part of all members. Instead, the agreement finally reached will represent the minimum number of voters required to form that effective coalition which involves a minimization of bargaining costs.
We have no historical experience with systems which involve representation through two houses that are completely diverse in their constituencies, and therefore we cannot check our conclusions by examining data from the real world. However, it is possible to get the same general result by another line of reasoning, which may serve as a partial check. In representative government the negotiating is done by the representatives. Each representative should vote for any measure or combination of measures which will be approved by a majority of his constituents and should attempt to arrange bargains satisfactory to such a majority. Given the arrangements of the constituencies with complete diversity, this simple policy on the part of each representative would lead to the same result that we obtained by analyzing the coalition formation in the two-house legislature. This is because the constituents for a single representative in each house include members of all constituencies in the second house, randomly distributed. The end result, in a system in which the representation is like that shown in Figure 21 but in which the square is 199 by 199, would be that in the mean case approximately 17,500 out of the 39,601 voters would have to approve a measure before it was passed. Of these about 2500 would be situated so that their votes would be necessary in both houses, and these voters would tend to be suitably rewarded for their luck.
Compared with the 10,000 voters necessary to control a one-house representative assembly, 17,500 is a distinct “improvement”—although it is still less than a majority of the voters; 17,500, in fact, is the number of voters that would be needed to pass a measure through a one-house legislature if a 7/8 legislative majority were required. Requiring a ¾ legislative majority in both houses would mean that a little over 24,000 voters would be necessary to pass a measure, of whom almost 6000 would be required in both houses. This is more than a majority and better than could be obtained by requiring unanimity in one house. That is to say, the over-all result would reflect a more inclusive “rule” than would the requirement of legislative unanimity in a one-house legislature, where each representative is elected by a simple majority of constituents.
In Chapter 9 it was stated that the bicameral legislative system automatically discriminates between measures in which the intensities of the desires or antipathies of the voters are equal and measures in which the minority has stronger feelings than the majority. We have thus far been discussing the latter case; let us now turn to the equal-intensity situation. The reader will remember from the discussion in Chapter 9 that, although equal intensities of feelings are most unlikely, the situation could arise if the differences in intensities among the voters were to be symmetrically distributed among subgroups of voters. Studies of the equal-intensity situation, therefore, are useful for such issues as were involved in the traditional idea of general legislation. In matters concerned with foreign policy, the criminal code, and promotion of scientific discovery, etc., it is possible that differences of opinion may well exist, and there is no reason to believe that all opinions will be held with equal intensity, but there is also no particular reason to expect the differences in intensity to be systematically distributed among particular groupings. Although such matters are a relatively minor part of the activities of most modern governments, they are of considerable importance and may well deserve special handling.
In this chapter we have thus far been discussing the intense-minority case; let us now turn to an equal-intensity case. Suppose that in a representative government which uses a single-house legislature, the members of which are elected by simple majority vote from separate constituencies, some issue comes up in which the intensities of the feelings of the voters are equal. Given that the electorate in each constituency is large and that there are quite a number of constituencies (which is the situation in real life), it is highly likely that a majority of the constituencies will have a majority reflecting a majority of the whole electorate. If this is so, then the representative assembly should vote in accordance with the wishes of the majority of the people, which is the “correct” decision in this case. In those cases (and they would be much less common) where the majority was concentrated in a minority of the constituencies, the representatives of those constituencies would be motivated to enter into bargains with the representatives of other districts with the result that the measure would still be disposed of as the majority wished. All of this follows from the fact that, in the equal-intensity case, minorities are unable to compensate members of the majority for changing their votes, while the members of the majority can readily compensate the minority for such changes.
If we consider the changes in this picture which would result from a bicameral legislature with complete diversity of representation, they turn out to be small. Again, if the number of voters is very large and the number of constituencies quite large, the laws of combinations and permutations would result in a majority of constituencies in both houses being in agreement with the majority of the whole population, so in most cases the two houses would simply enact the will of the majority. Cases in which the voters were distributed in such a way that they failed of a majority in one house or the other would be commoner than with a one-house legislature, but still relatively uncommon. As in the one-house system, bargains would not be particularly hard to arrange in such a case. Thus the switch from single-house to two-house representative government makes only a very slight difference in the way that equal-intensity issues are treated. There is a small increase in the cost of higgling, but that is all.
This contrasts sharply with the results for cases where the minority is more intense in its desires than the majority. As we have seen, in such cases logrolling leads to only a little more than ¼ of the voters being able to control a one-house legislature, while over 7/16 are necessary to control a two-house legislature. A rule which required the organizers of a logrolling coalition to obtain the approval of 7/16 of the voters in a one-house legislative system of representative government would require that the legislature, if it were elected by simple majority in individual constituencies, operate on a 7/8 majority rule, i.e., pass only bills which are approved of by 7/8 of its members. The 7/8 rule, however, would impose quite a heavy bargaining cost on equal-intensity measures. The two-chamber legislature, by automatically distinguishing between the two cases and imposing much greater restraints on the erection of coalitions by members of intense minorities than on majorities in equal-intensity cases, can perform a very valuable function.
The advantage gained by the use of the two-house legislature, however, is rather dissipated by the simple majority method of voting. Even in the two-house legislature the intense minority can pass its measures with less popular support than can an equal-intensity majority. This appears the opposite of what should be the case, but given the simple-majority voting rule nothing can be done about it. Departures from the simple majority rule, however, can improve the situation. For example, if methods of election of the representatives should insure that each house represents the whole people, not just a majority in each constituency, then a two-house legislature with simple majority voting in each house would require ¾ of the people to approve bargains of intense minorities, while still permitting passage of equal-intensity measures which were approved of by only simple majorities. This sounds utopian, but conceivable practical arrangements to obtain comparable results would be possible.
So far we have been discussing a two-house legislature in which there is “complete diversity” in the constituencies of the representatives in the two houses. In practice this situation is never found; however, partial diversity is almost universal in governments which use the two-house system. Partial diversity takes many forms, and for purposes of analysis we shall divide it into two subtypes: “arrangement” and “number” diversity. Number diversity is fairly common in its pure form in the real world (the United States legislative branch is an example), while arrangement diversity is almost never found in its pure form. In most cases the two are intermixed in two-house legislatures. We shall examine them in their pure form largely for simplicity, and we shall start with “arrangement” diversity for the same reason.
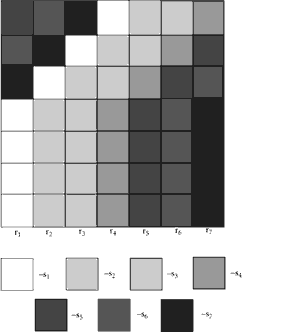 |
Figure 23 |
We have covered a completely diverse system of constituencies for a two-house legislature. At the other extreme we can easily imagine a completely nondiverse system. If the members of each house were elected from the same constituencies (that is, if each constituency sent a representative to each house), then the two houses would be identically constituted, and the situation, from our present standpoint, would not differ from a one-house legislature.*53 Using our diagram, it is possible to construct systems of representation which form a continuum from complete diversity to complete nondiversity. To illustrate “arrangement” diversity, see Figure 23. In this square matrix representing 49 voters, the columns denote constituencies in one house. A particular configuration can then be chosen to represent each constituency in the second house. Each senator shares 2, 3, 4, … 7 voters with some given representative. In Figure 23 we have chosen to give each senator 4 constituents in common with some single representative. For example, the blank squares represent the first senate constituency. Here the senator shares 4 voters with r1 and 1 voter each with r2, r3, and r4.
Obviously, as we proceed by small steps from complete diversity to complete nondiversity, the features of completely diverse systems which we have discussed gradually fade away. Semidiverse systems, however, have a special feature which neither completely diverse nor completely nondiverse systems share. Such systems, in effect, classify the voters into categories. For example, in Figure 23 the voters in the bottom four rows are represented in the Senate and in the House by representatives elected from the same constituencies, while the voters in the upper three rows are represented by diversely based legislators. The result is that it is much easier to work out coalitions which will benefit the people in the lower four rows than in the upper three. The costs of bargaining are lower because part of the bargain is already implicitly made by the arrangement of constituencies. Further, bargains involving only voters in the lower four rows will operate on a basis similar to that of the single-house legislature, while those involving voters in the top three rows will have to operate on the same basis as in a completely diverse system. Clearly, this system greatly favors the voters who are so arranged as to have the advantage of a sort of prefabricated bargain.
Although this situation is never exactly duplicated in real-life political organizations, something very like it is quite common. The American farmers, for example, possess what amounts to a built-in coalition in the two houses of our legislature. This gives them a great advantage over less fortunately situated groups.
Our second type of partial diversity is “number” diversity. Under the American constitution many Western voters are much more heavily represented in the Senate than the inhabitants of the more populous states. In the House, on the other hand, people from different parts of the country are more or less equally represented. This situation arises from the fact that each state has two senators, regardless of how sparse its population, while the representatives are distributed among the states according to population. The system has been criticized for giving the voters in the thinly populated states an unfair advantage. This “unfairness,” however, is not intrinsic in number diversity as a concept. It is easy to conceive of a system under which area A elects 5 representatives to the “House” and 1 to the “Senate,” while area B elects 1 to the “House” and 5 to the “Senate,” thus obtaining the advantages of number diversity without giving any voter more power than any other.
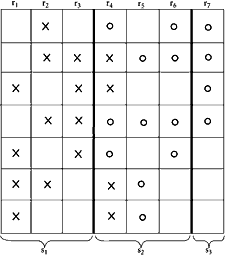 |
Figure 24 |
The system to which we are accustomed, however, does give the voters in some states an advantage over those in others. In the American system the constituency of most senators “includes” the constituencies of a number of representatives. As illustrated in Figure 24, the constituency for senator s1 includes the constituencies of representatives r1, r2, and r3. This type of diversity also leads to some improvements over the single-chamber legislature. Many coalitions which would pass in the House will fail in the Senate. For example, the voters marked X in Figure 24 could maneuver their bill through the House, but it would fail in the Senate. On the other hand, there would still be some bills that would be passed by this type of two-chamber legislature which would require only the very minimum of voter support in a one-chamber legislature, e.g., the one shown by the O’s on the diagram.
Two chambers differing from each other only in this way offer much less of a safeguard against the imposition of excessive “external cost” on the citizen than organization in accordance with what we have called “arrangement” diversity. Further, if the number of constituents varies from “senator” to “senator,” it may introduce an element of discrimination among the voters. Those who are in small constituencies have an advantage over those who are in large ones. Nevertheless, the device does, to some extent, improve the operating characteristics of a system of representative government.
There is also another phenomenon in the real world which can be regarded as an extreme version of number diversity. The President of the United States and many other “executives” are equipped with the veto power. This, in effect, constitutes them as a third house of the legislature. In this case, however, the “third house” represents the entire body of voters in one grand constituency. The President should, insofar as he uses his veto power as a simple legislative tool, follow the preferences of the majority of the voters. Therefore, he would accept only bargains which meet the approval of the majority of the populace, and hence could considerably raise the minimum size of the logrolling coalitions. Normally, of course, the President tends simply to sign most bills, and vetoes only a minority. Nevertheless, he has the power to constitute himself as a third legislative house, and the exercise of this power, whether explicit or implicit, materially improves the functioning of the American Constitution.

