The Calculus of Consent: Logical Foundations of Constitutional Democracy
By James M. Buchanan and Gordon Tullock
This is a book about the
political organization of a society of free men. Its methodology, its conceptual apparatus, and its analytics are derived, essentially, from the discipline that has as its subject the economic organization of such a society. Students and scholars in
politics will share with us an interest in the central problems under consideration. Their colleagues in
economics will share with us an interest in the construction of the argument. This work lies squarely along that mythical, and mystical, borderline between these two prodigal offsprings of political economy. [From the Preface]
First Pub. Date
1958
Publisher
Indianapolis, IN: Liberty Fund, Inc.
Pub. Date
1999
Comments
Foreword by Robert D. Tollison.
Copyright
The text of this edition is copyright: Foreword, coauthor note, and indexes ©:1999 by Liberty Fund, Inc. Content (including Preface) from The Calculus of Consent, by James M. Buchanan and Gordon Tullock, ©: 1962 by the University of Michigan. Published by the University of Michigan Press. Used with permission. Unauthorized reproduction of this publication is prohibited by Federal Law. Except as permitted under the Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a data base or retrieval system, without prior permission of the publisher. For more information, contact the University of Michigan Press: http://www.press.umich.edu. Picture of James M. Buchanan and Gordon Tullock: File photo detail, courtesy Liberty Fund, Inc.
- Foreword
- Ch. 1, Introduction
- Ch. 2, The Individualistic Postulate
- Ch. 3, Politics and the Economic Nexus
- Ch. 4, Individual Rationality in Social Choice
- Ch. 5, The Organization of Human Activity
- Ch. 6, A Generalized Economic Theory of Constitutions
- Ch. 7, The Rule of Unanimity
- Ch. 8, The Costs of Decision-Making
- Ch. 9, The Structure of the Models
- Ch. 10, Simple Majority Voting
- Ch. 11, Simple Majority Voting and the Theory of Games
- Ch. 12, Majority Rule, Game Theory, and Pareto Optimality
- Ch. 13, Pareto Optimality, External Costs, and Income Redistribution
- Ch. 14, The Range and Extent of Collective Action
- Ch. 15, Qualified Majority Voting Rules, Representation, and the Interdependence of Constitutional Variables
- Ch. 16, The Bicameral Legislature
- Ch. 17, The Orthodox Model of Majority Rule
- Ch. 18, Democratic Ethics and Economic Efficiency
- Ch. 19, Pressure Groups, Special Interests, and the Constitution
- Ch. 20, The Politics of the Good Society
- Appendix 1, Marginal Notes on Reading Political Philosophy
- Appendix 2, Theoretical Forerunners
 Majority Rule, Game Theory, and Pareto Optimality
Majority Rule, Game Theory, and Pareto Optimality
At several points in this book we have found, and shall find again, occasion to relate our analysis to that of modern welfare economics. This seems to be particularly useful following our application of elementary game theory to the operation of majority voting rules. By examining our results in comparison with the criteria of efficiency or optimality employed by the welfare economist, a somewhat better appreciation of the constitutional-choice problem may be achieved. To this point we have, in several instances, made reference to the Paretian criteria for efficiency. In Chapter 7 we discussed these criteria briefly. Additional discussion is wholly unnecessary for some readers, but even at the risk of introducing some redundancy, we shall first try to clarify the meaning of the fundamental Paretian construction.
Pareto Optimality
The criterion that the modern welfare economist employs in determining whether or not a given situation is “efficient” or “optimal” and whether or not a given move or change is “efficient” or “optimal” was developed by Vilfredo Pareto. We shall first define this criterion carefully, and we shall then distinguish two separate applications of the criterion.
The underlying premise of the modern Paretian construction is the purely individualistic one. The individual himself is assumed to be the only one who is able to measure or to quantify his own utility or satisfaction. No external observer is presumed able to make comparisons of utility among separate individuals. It is possible, however, even within these limits, to develop a means of evaluating either “situations” or “changes in situations” in terms of their “efficiency.” To do this, a very weak ethical postulate is advanced. The “welfare” of the whole group of individuals is said to be increased if (1) every individual in the group is made better off, or (2) if at least one member in the group is made better off without anyone being made worse off. Clearly this postulate must be accepted by those who accept any form of individualistic values, that is, those who consider the individual rather than the group to be the essential philosophical entity. The ambiguities in the terms “better off” and “worse off” are removed by equating these to the individual’s own preferences. If an individual shifts to position A from position B when he could have freely remained in B, he is presumed to be “better off” at B than at A.
On the basis of this construction, it becomes possible to define the property of a “social state” or “situation” that is necessary to insure its qualification as a Paretian P-point, that is, a point on a conceptual “optimality surface,” a surface that will contain an infinity of such points. If, in any given situation, it is found to be impossible to make any change without making some individual in the group worse off, the situation is defined as Pareto-optimal or Pareto-efficient. On the other hand, if, in a given situation, it is found possible to make at least one individual better off by a change while making no individual in the group worse off, this situation is defined as nonoptimal. The first use of the Pareto norm is, therefore, to provide a means of classifying all possible social states or situations into the Pareto-optimal set and the nonoptimal set. Central to this approach is the idea that no single “most efficient” situation can be located or defined.
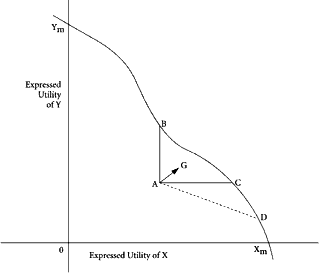 |
Figure 13 |
The second application of the Paretian construction lies in the development of a rule for classifying changes in social situations. A change is defined to be Pareto-optimal if, in the transition from one situation to another, either (1) every individual in the group is made better off, or (2) at least one individual in the group is made better off and no one is made worse off. It is important to note carefully just what this rule states, since much confusion has arisen in its application. It does not state that any shift from a nonoptimal to a Pareto-optimal situation is itself Pareto-optimal. The rule describes the characteristics of a change and does not relate directly to the characteristic of a situation or state either before or after change. A change away from an established Pareto-optimal situation cannot be itself Pareto-optimal, by definition. However, any other change may or may not be Pareto-optimal in itself. A change from one nonoptimal position to another may be Pareto-optimal, and a change from a nonoptimal position to a Pareto-optimal position may not be itself Pareto-optimal. These points can be easily illustrated in a simple diagram (see Figure 13). On the ordinate and the abscissa is measured the “welfare” or “utility” of individuals Y and X, measured in terms of their own expressions of preference. Any point along the frontier curve YmXm represents a Pareto-optimal situation or state. Any movement from such a point to another point on or inside the frontier must reduce the expressed utility of one of the two individuals. Assume an initial position at A. A change from A to any point on the frontier between B and C is clearly Pareto-efficient since both parties are made better off. However, a change from A to D is not itself Pareto-efficient since Y is made worse off in the process, even though the change represents a shift from a nonoptimal position A to a Pareto-optimal position D. On the other hand, a change from A to G is Pareto-optimal in itself, although it represents a shift from one nonoptimal position to another.*33
This very elementary review of the Pareto criterion has been developed here because it will prove helpful to us in subsequent stages of our analysis. In the remaining parts of this chapter we shall use the Paretian conceptual apparatus in examining the results of the application of game theory to majority voting rules.
Imputations and Pareto Optimality
Let us recall the initial three-person game of Chapter 11, which involved the sharing of a fixed-sum external grant among three separate road-repair projects. The solution set of imputations was:
Note that all of the imputations in F are Pareto-optimal: this is to say, there is no imputation outside the set which dominates any imputation in the set for all three individuals; there is no change from one of the imputations in F which could be made on the approval of all members of the group. This Pareto-optimality condition is imposed through the definition of the characteristic function which makes the return to the whole group,
along with that to any two-person majority coalition, such as
In more general terms, the condition required for an imputation to exhibit Pareto optimality is that the sum of the gains to all individuals be at least as much as the whole group could gain if the members chose to act as a grand all-inclusive coalition. In more formal terms, Pareto optimality is insured by
 |
(4) |
where xi is the return to an individual member of the group in a “solution” imputation, and v(In) is the expression for the return to all individuals acting jointly as an all-inclusive coalition.*34 In our particular example, Pareto optimality is guaranteed by the assumption that a positive-valued grant is received from some outside agency. The game here consists wholly of dividing this fixed-sized gain, and, unless wastage is involved in the process, the whole amount must be disposed. Therefore, any imputation, whether in the F set or not, is Pareto-optimal. Once divided, there is no way that side payments or compensations could possibly be arranged so as to move all members of the group to preferred or indifferently valued positions. This reflects the familiar point that the Pareto-optimality surface contains an infinity of points, each reflecting a separate distribution of “welfare” among members of the group.
In this initial example, the playing of the game is also Pareto-optimal, as distinct from the characteristic of the final solution: that is to say, the change in situation represented by the shift from the position prior to “play” to that after “play” is also Pareto-optimal. The preplay imputation is (0, 0, 0); thus, any final imputation represents individual positions which are either improvements or no worse than initial positions. The assumption that the grant is received from external sources also insures that the game itself will be Pareto-optimal. The individual-rationality condition,
 xi for every i in In,
xi for every i in In,as we have interpreted it in Chapter 11, is satisfied.
If we now modify the game and consider that one introduced in the last part of Chapter 11 in which road-repair funds are to be raised from general taxes, the individual-rationality condition no longer holds. The majority-rule game under these circumstances is no longer Pareto-optimal. The initial imputation in this case is (1/3, 1/3, 1/3), and, in any final imputation after “play,” one member of the group is moved to a less preferred position. Hence, the change represented by the game itself is nonoptimal in Pareto terms.
The solution imputation will continue to be Pareto-optimal, however, so long as condition (4) holds: that is, so long as the sum of the individual gains in any solution imputation is as much as the whole group could gain by acting through an all-inclusive coalition. However, so long as the solution imputation qualifies as a Pareto-optimal point, the playing of the game itself, in an expectational sense, may be considered “optimal.” That is to say, this restriction on the solution insures that the payoffs to the winners of the majority-rule game are at least equal to the losses incurred by the losers. Therefore, the expected payoffs to each individual, at the start of play, must be at least equal to the value of the initially held assets. Although the game itself, as finally played, must reduce the utility of some of the players and hence be nonoptimal, the game does not involve the reduction in the expected utility of any player at the time of the participation decision, provided only that the solution imputation qualify as Pareto-optimal. We are neglecting here the possible utility or disutility from play itself, as well as the possibility of diminishing marginal utility of income.
Need Solution Imputations Be Pareto-Optimal?
The results to this point are perhaps obvious, especially after the analysis of Chapter 11. The more interesting question is the following: Does a “solution” to the majority-rule game embody only imputations that are Pareto-optimal?
The game theorists seem to be rather unhappy about imposing this restrictive requirement on any solution to n-person games.*35 We may be able to shed some light on this question by a re-examination of our simple models. Suppose that the initial endowment is, as before assumed, (1/3, 1/3, 1/3). Further, let us assume that there exists no spending opportunity through which the group can increase its net real income. There are no “productive” public investments, and, in the private sector, opportunities are equalized at the appropriate margins of expenditure. In other words, the local roads simply do not need further repair, and, considered in additive cost-benefit terms, any repair project will yield less in benefits than it costs. To be specific, let us assume that the benefits yielded by repairing a road amount to only 5/6 of the costs. We shall assume full symmetry in benefit schedules: that is, public investment is equally productive on every road.
As we have put the problem, the initial imputation is Pareto-optimal. Will the group remain at this imputation? Or will majority voting move the group from an optimal to a nonoptimal position? Or from one optimal position to another?
Consider now the imputation (5/12, 5/12, 0) used before. Clearly, a shift to this imputation brings the group below the Pareto-optimality surface, but the imputation also dominates the initial one for the effective majority coalition, (1, 2) in this case. For the time being, let us label as D the set of imputations:
This set seems to yield “solution” imputations although no single imputation in the set is Pareto-optimal. By proposing the imputation (0, 7/12, 3/12), the third man can form a new coalition with the second, and they could carry decision. However, as in our earlier discussion, one and three may then combine and shift to (5/12, 0, 5/12) which is in D. The stability properties of imputations in D seem to be identical to those in F.
Luce and Raiffa state that the D set, which does not contain Pareto-optimal imputations, does not represent a set of stable imputations. They argue that only that set containing Pareto-optimal imputations will exhibit the required stability of solutions. Their argument seems worth examining in some detail.
They suggest that group rationality (Pareto optimality), expressed in condition (4), is immaterial since all solutions that are stable must lie within the set of Pareto-optimal imputations. Basing their discussion on the work of Shapley and Gillies, they isolate four classes of n-tuples of payments:
 is the set of n-tuples in X such that is the set of n-tuples in X such that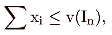 i in In |
(5) |
This states that 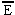 is the set of imputations for which the aggregate gains resulting from an all-inclusive coalition are greater than or equal to the summation of the gains received by the separate individuals through participation in the game, that is, in the imputations in X. In our numerical example here, the imputations listed fall within
is the set of imputations for which the aggregate gains resulting from an all-inclusive coalition are greater than or equal to the summation of the gains received by the separate individuals through participation in the game, that is, in the imputations in X. In our numerical example here, the imputations listed fall within 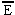 since, by hypothesis, the aggregate real income of the group is lowered by the action taken. In numerical units, the value of the left-hand side of condition (5) would be 5/6 and the value of the right-hand side would be 1.
since, by hypothesis, the aggregate real income of the group is lowered by the action taken. In numerical units, the value of the left-hand side of condition (5) would be 5/6 and the value of the right-hand side would be 1.
E is the set of n-tuples in X such that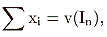 i in In |
(6) |
which is the same as condition (4) above. This is the set of Pareto-optimal imputations. The first three-person game yielded imputations that necessarily fell within E, regardless of their location within or without F. Games that are purely redistributional must yield imputations in E.
 is the set of n-tuples in is the set of n-tuples in 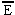 such that such thatxi 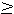 v({i}) for all players in In v({i}) for all players in In |
(7) |
This is the subset of 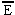 which represents final imputations in which all individuals have either improved their position by participating in the game or have not been made worse off. This is the condition of individual rationality, as interpreted, which we have discussed earlier. In slightly different terminology, this condition, if satisfied, insures that the game itself is Pareto-optimal, even though a position on the optimality surface may not be achieved.
which represents final imputations in which all individuals have either improved their position by participating in the game or have not been made worse off. This is the condition of individual rationality, as interpreted, which we have discussed earlier. In slightly different terminology, this condition, if satisfied, insures that the game itself is Pareto-optimal, even though a position on the optimality surface may not be achieved.
|
I is the set of n-tuples in E such that xi 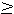 v({i}) for all players in In v({i}) for all players in In |
(8) |
This is a subset of the Pareto-optimal set of imputations. In particular, it is the subset of the Pareto-optimal set that may be attained in a Pareto-optimal manner from the initial no-play position. In other words, this set of imputations, on the Pareto frontier, can be reached by playing only “optimal” games.
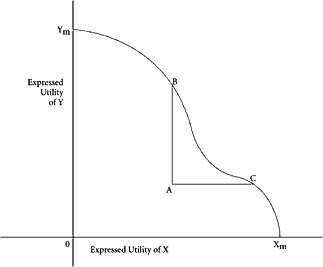 |
Figure 14 |
In a two-person model, which can be represented on a two-dimensional surface, each set of these n-tuples can be shown readily. Refer to Figure 14, which is similar to Figure 13.  is represented by the whole area enclosed by the two axes and the frontier YmXm. Any point along the frontier or inside the frontier satisfies the weak requirements of condition (5). E, the Pareto-optimal set, is represented by the set of points along YmXm, that is, on the frontier. Note that E is a subset of
is represented by the whole area enclosed by the two axes and the frontier YmXm. Any point along the frontier or inside the frontier satisfies the weak requirements of condition (5). E, the Pareto-optimal set, is represented by the set of points along YmXm, that is, on the frontier. Note that E is a subset of  . If A is defined to be the initial position, then
. If A is defined to be the initial position, then  includes the set of points enclosed by the area ABC. I is that set of points falling along the frontier between B and C, being a subset of
includes the set of points enclosed by the area ABC. I is that set of points falling along the frontier between B and C, being a subset of  .
.
Luce and Raiffa (pp. 216-18) accept a proof by Shapley to the effect that a stable solution in E must lie within E. Hence, they conclude that no real restriction is placed on the results by assuming group rationality (Pareto optimality) in the first place. A commonsense approach may reveal the reasoning here. Why are the imputations
suggested as “solutions” to the particular problem considered, unstable? No element in this set, which we have called D, dominates any other element; but is every imputation not in D dominated by one in D? This second requirement is the crucial one, and D clearly does not satisfy it. Consider the imputations
which we recognize as the F set. One of the elements or imputations in this set dominates each imputation in D, yet no element in D dominates all of the imputations in F. This suggests that D could not represent a set of stable imputations.
Let us consider the real-world implications of this proof. Note that the imputations in F are Pareto-optimal. However, in order to attain an imputation in this set, the playing of the game must result in a shift that is equivalent to a purely redistributive transfer of real income among individual members of the group. That is to say, the game must be constant-sum, as defined by condition (6). However, given the requirement that collective decisions must involve the employment of general tax revenues to finance public services, this constant-sum restriction disappears. Moreover, when this happens, the F set of imputations remains as the solution only if full side payments are allowed. If both purely redistributive transfers and side payments are excluded, the game is severely constrained. There is no need whatever for the solution to exhibit the Pareto-optimality property. Condition (6) need not be met. The conclusion here is clearly that, if a majority is to exploit a minority, the most “efficient” means of so doing is the imposition of simple redistributive transfers (lump-sum taxes) instead of the indirect means of general-tax financing of special public-service benefits (or, conversely, special-tax financing of general-benefit public services), which may, as in our example here, involve a net cost for the group considered as a unit.
In the more constrained game without side payments, the imputations in F cannot be said to dominate those in D. Dominance has meaning only if the coalition is effective in shifting from one imputation to another. The set of imputations, F, simply does not exist in the constrained model. The D set embodies the solution with the same stability properties as the F set in the more general model, unless the human proclivities to make side payments are considered to be so strong as to rule out meaningful discussion of such constrained games.
Geometrical Illustration
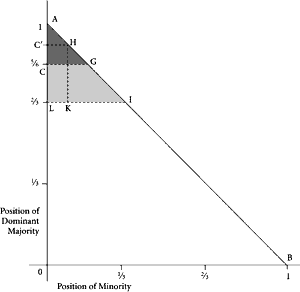 |
Figure 15 |
The essential points may be clarified by geometrical illustration. In Figure 15 below we measure on the ordinate the position of the dominant or the effective majority. The gains are added over the two members since we must use two-dimensional surfaces. On the abscissa we measure the position of the minority member of the three-man group. In the restricted model that we have been discussing, we assume that no investment in the public sector is productive. This makes the initial imputation Pareto-optimal; this imputation is (1/3, 1/3, 1/3), which becomes the point (2/3, 1/3) when plotted on the two-dimensional diagram as point I, which is, by definition, on the Pareto frontier. Since any division of one unit is also, by definition, on the frontier, the line AB in Figure 15 represents the whole set of Pareto-optimal points. Since we do not identify the members of the majority in the diagram and since the benefit schedules are symmetrical, if we allow individuals to shift from membership in the majority to membership in the minority, all points that are Pareto-optimal in the three-person model can be represented on AB. The set of imputations, F, the solution to the generalized game, is shown at A. At this point the member of the minority is deprived of all assets, and the two members of the majority coalition symmetrically share the gains, which are equivalent to the whole product. Again, by shifting separate individuals, A can be taken to represent all three of the imputations in F. As we have noted, if purely redistributive transfers should be allowed, a majority would immediately shift the group from I to A. Nothing would be modified except the distribution of the fixed-sum among the members of the group.
If redistributive action is excluded, the majority might still find it advantageous to take action, even though, by hypothesis, such action will be unproductive for the whole group. The point C represents the set of imputations D, defined as the solution to the more constrained model. Here the combined “gains” of the majority are 5/6, while the assets of the minority are confiscated. C is clearly beneath the optimality frontier. This suggests that, conceptually, all of the members of the group could be made better off by some change. The range of such changes is shown by the heavily shaded area in Figure 15. A shift or change from C to any point in this area would itself be Pareto-optimal. If side payments are allowed, the minority member of the group could, for example, “afford” to offer the majority IK, valued at KH by the majority, in order to allow all the group to shift to H instead of undertaking the action shown at C. The majority would, if allowed, accept this offer, but they need not stop there. They could, instead, try to outbargain the minority member and to force him to concede sufficient side payments to allow the group to move to A. The precise outcome of the actual bargaining process is unimportant; the relevant point is that such payments will insure that a final solution somewhere along the frontier will be reached. Under the specific conditions of this example, where the public project yields a total benefit value of 5/6, the relevant range on the frontier is AG. Side payments will be paid to the majority to prevent the investment from being undertaken.
The limits to resource wastage discussed in the last chapter can also be shown readily in this diagram. If all redistributive transfers and side payments are ruled out, any collective project that yields more than 2/3 to the effective majority will be selected. Any position on the vertical axis above L becomes a possible solution to the constrained game of majority rule.
Symmetry in Benefit Schedules
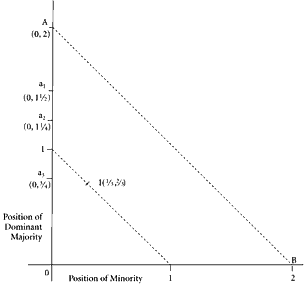 |
Figure 16 |
We have demonstrated clearly that majority voting rules may result in a shift of the group from a Pareto-optimal to a nonoptimal position in the constrained form of the game. It will now be useful to demonstrate geometrically that, if the initial position is nonoptimal and if an optimal position can be attained by collective action, majority voting will move the group to a Pareto-optimal position only if the benefit schedules are symmetrical over the whole group. Benefit schedules were assumed to be symmetrical in the previous example, where it was demonstrated that majority voting may shift the group off an initial position on the Pareto frontier. Symmetry in benefit schedules may be at most, therefore, a necessary condition for attaining a Pareto-optimal position. It can never be sufficient to insure the attainment of such a position. Refer to Figure 16. As before, we assume an initial (before play) position at I. However, let us assume that public investment in all three roads is equally productive, and highly productive. An investment of $½ on each road is assumed to yield a benefit value of $1. In this case the F set becomes
represented in Figure 16 as the single point A. Majority decision will tend to shift the group to A, which is on the Pareto frontier. The majority-rule game, as actually played, is not, of course, Pareto-optimal, since the minority member of the group is shifted to a lower utility level in the process of paying taxes to support the public projects beneficial to other members of the social group. In an expectational sense, however, the game is “optimal,” provided, of course, that the rules are “fair.” Note that, in this case, no introduction of purely redistributive transfers or side payments will change the result. The majority can reach the position shown at A only by undertaking the projects, and there is no way that the minority can make an effective counteroffer.
Note carefully, however, that this conclusion follows only when we assume symmetry in benefit schedules over all individuals.*36 If this assumption is dropped, the operation of majority-rule decision-making will not necessarily shift the group from an initial nonoptimal to a Pareto-optimal position without the introduction of side payments. For purposes of illustrating this point, we now assume that the investment of $½ on each road project will yield, respectively, $1, $½, $¼. The solution set becomes
assuming no side payments. Let us assume that there exist no investments in the private economy that are more productive than investment on the first road. If individuals 1 and 2 form a dominant majority, the group will shift to point a1 in Figure 16; if 1 and 3 form the majority, to point a2; if 2 and 3, to point a3. In none of these cases does majority voting shift the group to the optimality frontier, which could only be reached if all investment should be made on the first road.
When the benefits are asymmetrical, the frontier will be attained only if full side payments are allowed to take place. In the example here, Pareto optimality will be attained, after side payments, in the solution set:
If side payments are allowed, the first man can afford to pay the second man more than ½, the value of repairs to the second road, for his support of a policy of exclusive investment on the first road; and the first man could clearly pay the third man more than ¼, the value of his own estimated benefits from local road repair.
This introduces an extremely interesting point that we have deliberately neglected in the discussion of Chapter 11. In a purely formal sense, the imputations in F, written above, satisfy the Von Neumann-Morgenstern requirements for solution when full side payments are allowed. Moreover, since all three of the imputations satisfy the requirements jointly (that is, as a set of imputations), nothing further can be stated in terms of the formal construction. However, we have noted previously that the notions of stability and solution in n-person games generally are not fully satisfactory. Many games contain numerous solutions in the simple mathematical sense. Intuitively, we may see that these ideas of solution and stability are considerably less applicable to those games where benefit schedules are not symmetrical than to those in which such schedules are symmetrical. Let us consider the set F, above, more carefully. It seems clear that, of the three imputations in F, the second is more likely to emerge, or, to state this somewhat more correctly, the coalition represented by the second imputation seems more likely to emerge. Nor do some of the imputations in F seem more stable, under the restrictions of this model, than others outside the set. The second-imputation coalition between the first and the third person in the group seems more probable because the support of the third man for repair on the first road can be secured more “cheaply,” even with full money payments, than the support of the second man. This is because the relevant alternative, as considered by the third man, may be, not his combination with the second to exploit the first to the maximum, but his combination with the second to finance repairs to their own roads. If the third imputation is not considered by 2 and 3 to be a genuine alternative, then any imputation (c1, 0, c3), where 7/4 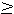 c1
c1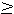 1, and 1
1, and 1 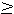 c3
c3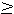 ¼, would be equally stable with (1, 0, 1). This point, which amounts to the denial that full side payments would be carried out in situations like the ones postulated, suggests the probable emergence of coalitions between those individuals and groups who are the direct beneficiaries of the most productive public projects and those individuals and groups for whom public investment is the least productive. This result will emerge, of course, only if some side payments are allowed. However, even if only limited forms of vote-trading are permitted, this general conclusion does not seem at all implausible and appears to be in accord with those reached in Chapter 10.
¼, would be equally stable with (1, 0, 1). This point, which amounts to the denial that full side payments would be carried out in situations like the ones postulated, suggests the probable emergence of coalitions between those individuals and groups who are the direct beneficiaries of the most productive public projects and those individuals and groups for whom public investment is the least productive. This result will emerge, of course, only if some side payments are allowed. However, even if only limited forms of vote-trading are permitted, this general conclusion does not seem at all implausible and appears to be in accord with those reached in Chapter 10.
Side Payments and Pareto Optimality
In a very real sense, the introduction of full side payments serves to create a marketable property right in the individual’s political vote, his power of collective decision. If this power is marketable (that is, if it is to command a price or a market value), some element of scarcity must be present. On single issues such as those discussed in our models, the scarcity of decision-making power is evident. Only one decision can ultimately be made; only one majority can be effective. The aggregate payoff function is reduced to the (1, 0) form. If collective decisions affect the disposition of economic resources, and if resources are used up over finite time, the decision-making power over any disposition of resources is scarce indeed. Decisions become irrevocable once made.
We have shown that only if side payments are introduced is there any assurance that majority-rule decision-making will lead to positions on the Pareto-optimality frontier. It will now be shown that this property depends solely on the introduction of side payments and that it has no specific connection with majority rule. In order to demonstrate this, we must prove that any decision-making rule, with full side payments, will produce only Pareto-optimal situations.
We may take two extreme decision-making rules, those of individual dictatorship and unanimity. First, we assume that all decisions for the group are to be made by a single individual, the dictator, who is interested only in maximizing his own utility. Let us keep within the limits of our simple three-person model, and again let us assume that the group receives a grant from external sources. The benefit schedules are as follows: if all funds are spent on the first road, $10; if all are spent on the second road, $5; if all are spent on the third road, $1. If Individual 1 is dictator, no question arises. However, if Individual 2 is dictator, he will find that his own utility can be maximized by “selling” his power of disposition over the external grant to Individual 1 for something in the bargaining range of $5 to $10. He will sell to the highest bidder, and it is evident in this model that Individual 1, for whom road repairs are the most productive, can bid highest. Similar conclusions follow if Individual 3 is dictator. A Pareto-optimal position is always attained. If the assumption of an external grant is dropped and general-tax financing assumed, this conclusion is not modified. The only difference here is that, with general-tax financing, the game itself is not Pareto-optimal. Under dictatorship, two of the individuals will tend to be made worse off as a result of any political action, always under the behavioral assumptions implicit in all of our models.
Let us now go to the opposite extreme and show that, even if a unanimity rule is adopted for collective decisions, all solution imputations will be Pareto-optimal when side payments are allowed. In the external grant case, any possible n-tuple or imputation dominating (0, 0, 0) for all three individuals can be attained through unanimous approval; or, if we are assuming tax financing from an initial position (1/3, 1/3, 1/3), any imputation dominating this may be a “solution.” Again, however, note that all repairs will be made on the first road, if side payments can take place. The set of possible solution imputations is extremely large here. The following three imputations represent the limits in the “negotiation set”:
If symmetry in gain is held to be characteristic of solution, a single imputation (3 1/3, 3 1/3, 3 1/3) emerges, but, as we have noted, the argument for symmetry seems much less convincing in games of this sort where all participants must agree on the sharing than it does in games such as that of majority rule. The final outcome will depend on the relative bargaining strengths of the parties in negotiation, but the bargaining will take place only to determine in what proportions the gains are to be shared. The Pareto frontier will tend to be reached, and it will be reached in a Pareto-optimal manner. The latter is the unique feature of the unanimity rule. The “game” itself is Pareto-optimal. Only with the unanimity rule will collective decision-making produce changes that are necessarily Pareto-optimal.
If side payments are not allowed, neither dictatorship nor the unanimity rule will produce imputations on the Pareto frontier in all cases. The unanimity rule will always result in movement toward the frontier, but there is no assurance that the frontier or surface will be reached. Thus, we find that the Pareto criterion suggests the paradoxical conclusion that open buying and selling of political votes may actually lead to an “improvement” for the group, measured in the extremely weak ethical sense of making everyone in the group better off as a result. This conclusion deserves more careful attention, but we propose to delay this to a later point. What has been demonstrated is that, without side payments, there is nothing in any particular voting rule to insure that collective decisions will move the group to the Pareto-optimality surface or that such decisions will keep the group on this surface if it is once attained.

