The Calculus of Consent: Logical Foundations of Constitutional Democracy
By James M. Buchanan and Gordon Tullock
This is a book about the
political organization of a society of free men. Its methodology, its conceptual apparatus, and its analytics are derived, essentially, from the discipline that has as its subject the economic organization of such a society. Students and scholars in
politics will share with us an interest in the central problems under consideration. Their colleagues in
economics will share with us an interest in the construction of the argument. This work lies squarely along that mythical, and mystical, borderline between these two prodigal offsprings of political economy. [From the Preface]
First Pub. Date
1958
Publisher
Indianapolis, IN: Liberty Fund, Inc.
Pub. Date
1999
Comments
Foreword by Robert D. Tollison.
Copyright
The text of this edition is copyright: Foreword, coauthor note, and indexes ©:1999 by Liberty Fund, Inc. Content (including Preface) from The Calculus of Consent, by James M. Buchanan and Gordon Tullock, ©: 1962 by the University of Michigan. Published by the University of Michigan Press. Used with permission. Unauthorized reproduction of this publication is prohibited by Federal Law. Except as permitted under the Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a data base or retrieval system, without prior permission of the publisher. For more information, contact the University of Michigan Press: http://www.press.umich.edu. Picture of James M. Buchanan and Gordon Tullock: File photo detail, courtesy Liberty Fund, Inc.
- Foreword
- Ch. 1, Introduction
- Ch. 2, The Individualistic Postulate
- Ch. 3, Politics and the Economic Nexus
- Ch. 4, Individual Rationality in Social Choice
- Ch. 5, The Organization of Human Activity
- Ch. 6, A Generalized Economic Theory of Constitutions
- Ch. 7, The Rule of Unanimity
- Ch. 8, The Costs of Decision-Making
- Ch. 9, The Structure of the Models
- Ch. 10, Simple Majority Voting
- Ch. 11, Simple Majority Voting and the Theory of Games
- Ch. 12, Majority Rule, Game Theory, and Pareto Optimality
- Ch. 13, Pareto Optimality, External Costs, and Income Redistribution
- Ch. 14, The Range and Extent of Collective Action
- Ch. 15, Qualified Majority Voting Rules, Representation, and the Interdependence of Constitutional Variables
- Ch. 16, The Bicameral Legislature
- Ch. 17, The Orthodox Model of Majority Rule
- Ch. 18, Democratic Ethics and Economic Efficiency
- Ch. 19, Pressure Groups, Special Interests, and the Constitution
- Ch. 20, The Politics of the Good Society
- Appendix 1, Marginal Notes on Reading Political Philosophy
- Appendix 2, Theoretical Forerunners
 Qualified Majority Voting Rules, Representation, and the Interdependence of Constitutional Variables
Qualified Majority Voting Rules, Representation, and the Interdependence of Constitutional Variables
The analysis of the simple majority voting rule can be extended without difficulty to cover more or less inclusive rules for reaching collective decisions. The results from this sort of extension will be apparent to those who have understood and accepted the analytical models of the preceding chapters. If less than a simple majority should be required for carrying a decision, the expected external costs would be greater, but the costs of reaching the necessary agreement among members of the effective coalition would be lower than under the operation of simple majority rules. If more than a simple majority should be required for decision, the expected external costs would be reduced, but the decision-making costs would be increased.
Given the behavioral assumptions of our models, individuals will tend to make collective decisions by organizing themselves in the smallest coalitions defined as effective by the decision-making rules, and, for members of dominant coalitions, the gains will tend to be shared symmetrically. Larger coalitions than those necessary for decision will not tend to emerge for two reasons. First, a larger-than-necessary individual investment in strategic bargaining will be required. Secondly, a smaller individual share of the gains from collective action will result in the larger-than-necessary coalition. If we relax our behavioral assumptions or if we introduce specific uncertainties about individual bargains into the analysis, these results will be modified. However, it seems useful to remain for the time being within the strictest limits of the original analysis.
As we prohibit full side payments on single issues and introduce logrolling as an imperfect system of vote-trading, the analysis of simple majority voting can also be applied to other voting rules. Coalitions will be formed embodying reciprocal support over a sequence of issues, and these coalitions will also tend to be of the minimum effective size.
Only one interesting analytical point seems worth raising. Intuitively, it seems plausible to expect that the more inclusive voting rules will tend to produce “solutions” that are somewhat more stable than less inclusive rules. For example, a rule which requires a three-fourths majority may appear to produce more stable solutions than one which requires one-fourth. Such an inference may not, however, be correct. While larger investment in bargaining will be required the larger the coalition that is needed for decision, the reward to the individual member will also be less the larger the coalition. The “price” at which individuals can be induced to abandon the coalition will tend to be lower in the larger coalition than in smaller ones. There are thus two opposing effects on the stability of the solutions produced by the operation of voting rules, and any general conclusions relating the stability properties to the rules themselves would probably be premature.*44
We do not propose to discuss further the extension of our analysis to simple voting rules, that is, to rules representing merely changes in the fraction of the total population required to reach collective decisions. The remainder of this chapter and the following chapters will be devoted to a discussion of two somewhat more complex modifications of our models. In this chapter we shall discuss the applicability of our analysis in moving beyond direct democracy to representative government. As we introduce representation, we shall find it necessary to consider four basic constitutional variables and their interrelationships. In Chapter 16 we shall consider the effects of introducing dual representation in two-house legislatures while retaining simple majority voting rules in each house. From these two still elementary models it should be clear that the basic analysis can be extended to a rather bewildering and complex set of possible institutional structures, many of which are to be found in real-world political systems. We do not, however, propose to make such extensions in this book.
Representative Government
Direct democracy, under almost any decision-making rule, becomes too costly in other than very small political units when more than a few isolated issues must be considered. The costs of decision-making become too large relative to the possible reductions in expected external costs that collective action might produce. If direct democracy were required, the individual, in his presumed role as constitutional choice-maker, would leave many traditional activities of the State to be organized in the private sector, and, for those few activities that he chose to collectivize, he would tend to adopt the less inclusive decision-making rules. In terms of our models, one means of reducing the interdependence costs generally is through the introduction of representative government. This step serves to shift downward the decision-costs function that we have previously employed several times in analyzing constitutional decisions.
If we utilize the models developed in Part II, it becomes relatively easy to construct a conceptual normative theory for the “optimal” degree of representation. At the one extreme, we have direct democracy in which the number of individuals directly participating in collective choice (the number of “representatives”) and the number of individuals in the total voting population stand in a one-to-one correspondence. At the other extreme, we have a single individual who “represents” or chooses for the whole group. In either of these two extreme cases, the constitutional-choice problem is greatly simplified. In the case of direct democracy, the single choice to be made, once a basic organizational decision is assumed, concerns the rules under which collective action shall be taken. Under the other extreme dictatorship model, the rules for collective action are set; the only choice facing the conceptual constitution-maker concerns the rules for choosing the dictator. In any of the models falling between these two extremes, both of these choices must be faced. Rules for choosing representatives must be determined, and rules for deciding issues in legislative assemblies must also be laid down. In addition, there is a third choice that must be faced, a choice that is assumed to be resolved in the two extreme models. The degree of representation must be chosen: that is to say, the proportion of the total population to be elected to the representative assembly must be selected. Finally, to all of these choices a fourth must be added: namely, the selection of the basis for representation. We shall refer to these as the four essential constitutional variables.
Consideration of the complexities introduced by these several constitutional-choice problems reveals the abstract and highly simplified nature of our direct democracy models, in which we were able to eliminate all of the choices except the one relating directly to decision-making rules. In a more general context it is evident that the four constitutional problems are interrelated, and, ideally, the individual should reach a decision on all four variables simultaneously. The basis of representation and the degree of representation indicated to be most “efficient” will depend surely on the rules through which representatives are to be selected and the rules which are to be required to carry decision in the legislative assembly. The separate variables can only be discussed individually in partial terms: that is, we may assume three of the variables to be fixed while discussing the fourth. Essentially this is what we have done in our earlier chapters. If we assume that the rules for selecting representatives are given, and that the degree of representation and the basis of representation are predetermined, our models may be applied directly to the setting of the rules for decision in legislative assemblies. On the other hand, if we assume these latter rules to be given, along with the degree and the basis of representation, we may apply our analysis to the selection of rules for selecting representatives without major analytical changes being required. The problems of determining the degree and the basis of representation are similar, but they seem sufficiently different to warrant some detailed consideration.
The Degree of Representation
We now want to consider only the choice concerning the degree of representation. Let us assume that representatives are to be chosen by simple majority voting rules, that the basis of representation is geographical, and that the unicameral legislature is to reach all decisions by majority voting. All of the constitutional variables are thus fixed except that which defines the proportion of the population that will sit as “representative” for the whole population in the assembly.*45
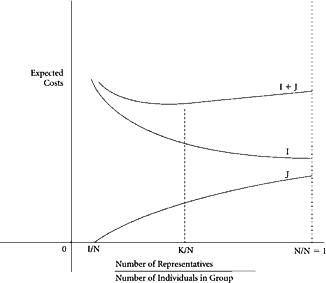 |
Figure 18 |
Within the restrictions of this model, we can derive costs functions that are quite similar, but not identical, to those which we have previously employed. Figure 18 illustrates. On the ordinate we measure expected costs, as before, but on the abscissa the quantity measured is different from that of earlier models. Here we measure the proportion of the group to be selected as members of the representative assembly. As before, we may now derive an external-costs function and a decision-making-costs function. They will have the same general shape as before. Let I represent the expected external-costs function. This will tend to slope downward because surely the individual will recognize that his own interests will be represented more adequately and more faithfully the more closely the representation approaches the full membership of the group. Note that, even at N/N, external costs are expected to be positive. This is because we have assumed a single rule, majority voting, in the legislative assembly. The positive value of the function at N/N, therefore, suggests that even with direct democracy the individual will expect to be in the losing coalition on some occasions.
Let J represent the decision-making-costs function. This will rise as the legislative assembly becomes larger because, given any rule, the costs of securing agreement increase. For example, let us suppose that the total group is made up of 100 persons. If one representative in 20 is selected, we should have a legislature composed of 5 persons, and, under simple majority rule, the agreement of 3 persons would be required for decision. On the other hand, if one representative in 10 is selected, we should have a legislature of 10 members, and a majority of 6 persons would be needed for decision. Clearly, the costs of securing agreement among 6 persons are greater than those of securing similar agreement among 3. As before, we may now add these two costs functions vertically, securing the curve I + J in Figure 18. The “optimal” degree of representation is shown where K/N of the total group are chosen to sit in the legislative assembly.
This analysis is simple and straightforward, but unfortunately it is also rather useless as it stands. Nevertheless, some interesting implications do emerge. First of all, the functional relationships described above are clearly affected by the size of the total group. As N becomes larger, the decision-costs function in Figure 18 will tend to shift upward. By comparison, the external-costs function, I, seems likely to be more directly influenced by the proportion of the population sitting in the assembly than by the size of the total population. If this is true, this function will be less affected by shifts in the over-all size of the group than the decision-costs function. The implication seems to be that the costs-minimizing solution is reached at a lower fraction of the total group in larger groups than in smaller groups. This implication seems intuitively obvious, but it does provide us with a quasi-empirical check on the conceptual validity of our general analytical models. It also helps to rationalize the common practice of democratic governments to lower the fraction of the population in the representative assembly as the population grows. They tend to do this by maintaining approximately fixed-sized representative assemblies.
A second, and less obvious, implication follows directly from the first. Since decision-making costs increase as the group grows larger, and since there seems to be no reason to expect that external costs will decrease, the total costs expected to arise from collective organization of activity, under any given rules for legislative decision-making, will tend to be higher in large groups than in small groups. This suggests that the basic organizational decisions will be affected by the size of the group; ceteris paribus, the larger the size of the group, the smaller should be the set of activities undertaken collectively.
The Basis of Representation
The constitutional variable that we have called “the basis of representation” is difficult to analyze in precise quantitative terms. Meaningful analysis does seem possible, however. First of all, let us “freeze” the other three constitutional variables. We shall assume that a simple majority of constituents is required to elect a representative who can normally be expected to act in a manner that will please a majority of his constituents. We shall also assume that the number of representatives in the legislature is fixed, and that a simple majority rule is to be adopted for decision-making in the legislature. The only variable left free for determination is the one that defines the basis upon which the representatives are to be selected from among the whole population.
We may proceed by examining the extreme cases. Conceptually we can think of a basis for representation that embodies a deliberate attempt at randomizing individual variations of political interest. For example, suppose that individuals should be classified into constituent groups solely on the basis of beginning letters of their surnames. Each group, appropriately adjusted in size with other groups, would be authorized to elect a single representative to the legislative assembly. Under this or any other roughly similar basis for representation, we should expect little or no convergence of special-interest groups behind particular representatives on any continuing or permanent pattern. Relatively, the most important stage for coalition formation in these circumstances would be at the level of electing the representative. The individual would anticipate significant external costs at this level of the political process; his own “representative” would effectively support his interest (would “represent” him) only if the individual voter should belong to the winning or majority coalition. Different coalitions would, of course, emerge in different constituencies, and some external costs would be expected to be produced by the actions of the legislative assembly. However, under the circumstances postulated, the individual citizen should be, relatively, more interested in the rules under which representatives are to be selected and in the degree of representation than in the rules for final legislative decision.
In this model (which we will call the “randomized-basis” model) vote-trading would take place at all levels, but it would be most pronounced at the level of electing representatives and would take the form of implicit logrolling. The individual who sought to be elected to the representative assembly would find it necessary to offer a “package” program sufficiently attractive to encourage the support of a majority of his constituents. Since, by hypothesis, the separate interests of his constituents correspond in range to those of the whole social group, he will include in the “package” many special programs designed to appeal to the strongly expressed interests of minority groups.
In the simplest “randomized-basis” model, there would be no assurance that similar “packages” would even be presented to each group of constituents, and very slight probability that the elected representatives to the assembly could be grouped readily into identifiable positions. Each representative might reflect a wholly different configuration of interests.
Certain statements can be made concerning the over-all characteristics of such a system of representation. By and large, it would seem that the expected external costs of collective action should be lower than under alternative bases of representation. The randomized basis would probably offer somewhat greater protection against the deliberate exploitation of specific minority interests, assuming fixed values for the other three constitutional variables. On the other hand, the costs of reaching collective decisions would probably be quite high in this model. Bargains of complex nature would have to be arranged at the level of selection of representatives, and exceedingly complex bargains might be required for the functioning of the legislative process.
Let us now consider a model at the opposite extreme. Assume that a purely functional basis for representation is selected. That is, assume that each definable interest group in the population is allowed to select a representative or representatives as members of the legislative assembly. The contrast with the first model is sharp and clear. If individual interests are homogeneous over reasonably large groups of individuals by identifiable functional characteristics, there will be relatively little difference in the various rules for electing representatives. The individual, in making constitutional choices, will only be interested in seeing that a member of his group (union, trade association, or professional society) sits in the assembly and that the membership of the latter is distributed over the different groups so that “adequate” representation is provided his own group. The expected external costs in this model will be concentrated on the prospects of adverse legislative decisions, not on the prospects of electing representatives who will not effectively act on behalf of individual voters. From this it follows that the rules for legislative decision will be the important constitutional variable under this basis for representation.
It seems obvious that decision-making costs will be considerably lower in this than in the randomized-basis model. On the other hand, expected external costs will surely be higher, assuming, of course, that the rules for selection and for decision are fixed. If we should want to diagram the selection of a basis for representation in terms of two costs functions similar to those employed several times before, we could, conceptually, think of starting at the left with the functional representation basis and proceeding to the right as we approach the purely randomized basis. If this were done, the curves so drawn would slope in the same directions as in the earlier problems, and, conceptually, an “optimal” basis of representation could be chosen—”optimal” being defined here in terms of the “ideal” mix of random and functional elements in the basis.
Geographic representation, the standard basis for at least one house in the legislatures of most Western democratic countries, falls somewhere between the two extreme models discussed above—between purely randomized representation and purely functional representation. If, in fact, individuals and groups were distributed randomly over space with reference to their political interests, geographical representation would approximate the first model. On the other hand, if separate political interests should prove to be primarily geographical, the second model would be more closely approached. We know, of course, that elements of both random and functional representation are present in the geographical basis. Within single constituencies there is normally to be found a reasonably wide range of voter interests, but there also remain many political issues which involve differential geographical impact. On such issues the geographical basis becomes similar to the purely functional in effect. Geographical representation is similar to majority voting in that, a priori, there is nothing that can be said for it as regards superiority over other possible bases.
The Structure of Control in Representative Democracy
The costs implicit in the substitution of representative democracy for direct democracy are of the category that we have denominated “external costs.” Bargaining costs are reduced by the use of the representatives. The costs which would arise from attempting to govern the whole United States through direct majority voting are so extreme that the representative system is acceptable even though it does markedly increase the external costs. In order to examine the external costs created by the representation device, let us construct a simple model. Consider a society composed of 25 voters who organize themselves into 5 constituencies of 5 each for the purpose of appointing representatives to conduct their mutual affairs (Figure 19).*46
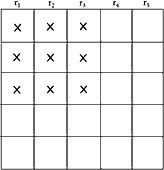 |
Figure 19*47 |
As a first approximation, let us suppose that the representatives, r1 … r5, simply vote as the majority of their constituents want them to. Under these circumstances a measure favored by nine voters, arranged like those marked X in the diagram, will be adopted. In the real world, as the number of voters and constituencies increases, the minimum-sized coalition required for dominance under simple majority voting approaches ¼ of all voters as a limit. For example, if there should be 39,601 voters arranged in 199 constituencies of 199 voters each, only 10,000 voters would have to favor an issue to secure passage (only 100 more than ¼ of all the voters). Thus, a logrolling bargain to obtain benefits from the political process need only involve about ¼ of the voters under a representative system. Therefore, representative institutions of this type are almost equivalent to permitting any group of ¼ of the voters in direct democracy to form a logrolling coalition empowered to determine what roads will be repaired, which harbors dredged, and which special interest groups will receive government aid. At this stage in the book it should not be necessary to point out how great the external cost imposed by such a procedure would be.
These external costs imposed by representative voting would be moderated by two factors. In the first place, not just any group of ¼ of the voters could win. It would be necessary for the group to be approximately equally distributed among a bare majority of the constituencies and absent in the remainder of the constituencies. This fact (which has already been discussed) would presumably put some, although not very onerous, restrictions on the bargains which could be struck. The type of project which is traditionally associated with the pork barrel—a small item benefiting a small group of voters, most of whom are within one constituency—would be little handicapped by this factor. Bargains intended to benefit groups spread through several constituencies, however, will be harder to negotiate, and groups spread through more than a majority of the constituencies will find profitable bargains extremely hard to arrange.
The second limiting factor lies in the organization of the bargaining process. Instead of each voter entering into bargains with other voters, the bargains are negotiated entirely by the representatives. This undoubtedly reduces the total-bargaining cost as compared with attempting to make bargains directly among millions of voters, but it also introduces sizable imperfections in the “market,” and these may affect (either positively or negatively) the external costs. In offering themselves for election, representatives offer to the voters in their constituencies a “platform” embodying that which they propose to accomplish. The individual voter then judges which of the competing candidates’ platforms is most to his liking, discounting this judgment by his estimate of the likelihood of the various candidates’ succeeding in making their promised bargains in the representative body, and casts his vote accordingly. The result is not precisely equivalent to that which would be expected under direct bargaining, but we do not propose to consider the differences in this work.
In general, legislative bodies are designed with two chambers (a subject discussed in the following chapter), but there are some countries which have either a one-chamber legislature or a two-chamber legislature with one chamber having greatly restricted powers. We might expect governments depending on this device to be highly inefficient, but an examination indicates that they frequently have mechanisms which, in essence, change the nature of the system enough to avoid the consequences that we have been discussing. Most of the small North European democracies, for example, follow a voting system under which the voter opts for a party and then the parties are given votes in the legislature in proportion to their respective totals. Although this system has its disadvantages,*48 it does have the advantage of providing what amounts to a unanimity system in selecting members of the representative body. All voters, not just the majority of each constituency, are represented in the legislature. Consequently, a majority of the legislature represents a majority of the voters, not just ¼+ as may be the case in a logrolling or party coalition when the members are elected from single-member constituencies.
Interdependence among Constitutional Variables
We have emphasized that the four basic constitutional variables introduced by representative government are interdependent. The “optimal” or “equilibrium” value for any one variable will depend on the values for the remaining variables, and, conceptually, the fully rational constitutional choice will embody the results of a simultaneous determination of all four variables, along with the more fundamental organizational decision concerning whether or not an activity or a set of activities is to be collectivized at all. We know, of course, that the variables may not be set simultaneously at their “optimal” values. Even at the highly abstract level of analysis characterizing our discussion, it will be useful to examine more carefully the interdependence among these variables. This examination will be helpful in demonstrating that our basic model may be applied to a wide range of constitutional-choice problems. We should be able to indicate some of the directions of change in the “equilibrium” values for remaining variables that would result from exogenous or externally imposed changes in single variables. In terms of a specific illustration, we should try to predict the direction of change in, say, the legislative-assembly rules for decision that would be suggested as a result of an externally imposed shift from a randomized basis to a functional basis of representation in the assembly. Or, to introduce a second illustration, we may be able to suggest the “desirable” change in the degree of representation indicated as a result of changing the rules for electing representatives.
In order to discuss these interrelationships carefully, we shall find it useful to define the separate constitutional variables:
X1: defined as the variable that describes the rules for electing members to the legislative assembly. It will assume fractional values ranging from 1/N to N/N or 1 as the election rule becomes more inclusive. An increase in X1 shall be interpreted as a shift from a less inclusive to a more inclusive rule for electing a representative, say, from a simple majority to a two-thirds majority.
X2: defined as the variable that describes the basis of representation of members of the assembly. As suggested, this variable is somewhat more difficult to conceive in quantitative terms than the others, but we may think of various “mixes” of functional and random elements. An increase in X2 shall be interpreted as a change in the weights of the two elements, with functional aspects becoming less pronounced and randomized aspects becoming more pronounced. By way of illustration, an increase in X2 would result from an increase in the number of delegates-at-large in a state assembly.
X3: defined as the variable that describes the degree of representation. It will assume fractional values ranging from 1/N to N/N or 1 as the degree of representation ranges from dictatorship to direct democracy. An increase in X3 shall be interpreted as an increase in the numerical value of the fraction, that is, as a move in the direction of direct democracy.
X4: defined as the variable that describes the rule through which the legislative assembly shall reach its decisions. It will assume fractional values ranging from 1/N to N/N or 1 as the rule becomes more inclusive. An increase in X4 shall be interpreted as a shift from a less inclusive to a more inclusive rule for decision, that is, as a shift toward the rule of unanimity.
Our whole analysis here is normative in the sense that we are considering the calculus of the individual as he faces constitutional choices. The four variables are interdependent in this rational calculus. There is no necessary interdependence in any other institutional sense. This individual, as he considers these variables, will be able to construct four independent relationships which will, in turn, enable him to solve the system for four unknowns. We may summarize this set of relationships by (9) given below.
| F (X1, X2, X3, X4) | (9) |
We may assume that the individual whose calculus we consider is initially in full “constitutional equilibrium.” This means simply that we assume that he has selected values for the four variables that seem most suitable from his own point of view. In mathematical terms, he has minimized total interdependence costs as a function of the four variables.
| min y = F (X1, X2, X3, X4) | (10) |
This function is, of course, minimized when the set of simultaneous equations represented by (11) is solved.
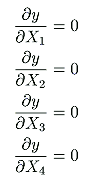 |
(11) |
We want now to examine the effects on these “equilibrium” values that will be exerted by imposing exogenous changes on the variables, one at a time. That is to say, let us suppose that an exogenous change forces X1 to take on some value other than its “equilibrium” value. Let us label this exogenously determined, nonequilibrium value for X1 as 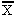 1. We ask the question: Granted this change in the value for X1, what values should the other variables, X2, X3, X4, take in order to minimize total interdependence costs in the new situation, that is, in that situation where
1. We ask the question: Granted this change in the value for X1, what values should the other variables, X2, X3, X4, take in order to minimize total interdependence costs in the new situation, that is, in that situation where 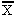 1 cannot be modified? The problem is the same as before. We seek to minimize total interdependence costs; but, since one of our four constitutional variables is fixed exogenously, we must solve a system of simultaneous equations in only three variables.
1 cannot be modified? The problem is the same as before. We seek to minimize total interdependence costs; but, since one of our four constitutional variables is fixed exogenously, we must solve a system of simultaneous equations in only three variables.
min z = F (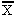 1, X2, X3, X4) 1, X2, X3, X4)
|
(12) |
This is accomplished when the following set of equations is solved.
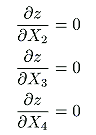 |
(13) |
What we want to determine now is the difference in the solution values for X2, X3, and X4 in equations (11) and in equations (13). Since these differences are generated by the initial exogenously imposed change on X1, we may represent them in the following form.
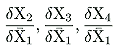 |
(14) |
These symbols represent the changes in the “equilibrium” values for X2, X3, and X4 that are generated when X1 is exogenously changed from its initial “equilibrium” value, X1, to its new value, 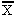 1.
1.
To bring this discussion back to our basic constitutional problem, suppose that a satisfactory constitution exists but that the migration of persons over space shifts the established geographical basis of representation from one that was close to the randomized-basis model to one that is significantly more functional in nature. What should the rational individual, if he were confronted with the opportunity to choose, do as regards the possible changes in the rules for selecting representatives, the possible changes in the size of the representative assembly, and the possible changes in the rules for decision in the assembly?
The whole set of effects that we want to examine may be summarized in the form of the following matrix, (15) below, using the symbols as developed in (14).
 |
(15) |
Each element in this matrix represents the effects on one variable that will result from changing the value of one other variable, assuming that the individual whose calculus we are considering reacts to the exogenous change by seeking to minimize total interdependence costs. For example, let us look at the last entry in the first row, dX4/d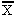 1. This represents the change in the equilibrium or optimal value for X4 that would result from the exogenous change represented by shifting X1 to some arbitrarily determined value,
1. This represents the change in the equilibrium or optimal value for X4 that would result from the exogenous change represented by shifting X1 to some arbitrarily determined value, 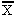 1. In terms of the specific meaning attached to these symbols, dX4/d
1. In terms of the specific meaning attached to these symbols, dX4/d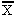 1 indicates the change in the rules for decision in the legislative assembly that the individual might consider desirable as a result of an exogenously imposed change in the rules for electing representatives.
1 indicates the change in the rules for decision in the legislative assembly that the individual might consider desirable as a result of an exogenously imposed change in the rules for electing representatives.
It is clear that we cannot expect to do more with this analysis than to indicate the directions of change: that is, we cannot do more than to insert the signs for the symbols in matrix (15). However, this in itself can possibly provide us with a significant amount of information.
Let us now concentrate on the first row. The elements, dX2/d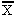 1, dX3/d
1, dX3/d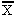 1, dX4/d
1, dX4/d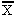 1, represent the changes that would be generated in X2, X3, and X4, respectively, by externally imposed changes in X1, defined as the rule for electing representatives to the legislative assembly. As this rule is made more inclusive (for example, as X1 increases in value from (N/2 + 1)/2 to 2N/3), the decision-making costs at this level of collective action will increase.
1, represent the changes that would be generated in X2, X3, and X4, respectively, by externally imposed changes in X1, defined as the rule for electing representatives to the legislative assembly. As this rule is made more inclusive (for example, as X1 increases in value from (N/2 + 1)/2 to 2N/3), the decision-making costs at this level of collective action will increase.
We may note first of all that any exogenously imposed change from the initially assumed “equilibrium” set of values for the constitutional variables must result in an increase in over-all interdependence costs. This follows from the fact that the initial situation is, by definition, “optimal” for the individual in question. In responding to the exogenously imposed change in the single variable under consideration, the individual will, however, attempt again to minimize interdependence costs, within the limits of the new set of constraints. As we have suggested above, the increase in X1, defined as the inclusiveness of the rule for electing representatives to the legislative assembly, will increase decision-making costs. The change will also reduce external costs,*49 but not to the extent that decision-making costs are increased. If no change in the other constitutional variables is allowed to occur, the individual will find himself devoting more resources to the making of collective decisions than he would choose if given the opportunity. While he will be somewhat more protected than before the change from the dangers of adverse collective action, he will want to consider how he might modify those constitutional variables remaining within his control. Specifically, what changes will the individual desire to make in X2, X3, and X4 in response to the change imposed on X1?
Note that we have specifically defined each of the constitutional variables in such a manner that an increase involves an addition to decision-making costs and a reduction in external costs. We are now inquiring about the changes in X2, X3, and X4 that will result from an increase in X1. The direction of change in the three variables will depend on the type of relationship that exists among the separate variables. It seems reasonable to suppose that these variables are mutually compensating in the individual’s calculus: that is to say, he will try to shift to a new position of equilibrium by changing those variables remaining within his power of choice in such a manner as to compensate or to offset the initial change imposed on X1. More specifically, he will try to shift the values for the variables X2, X3, and X4 in the directions that will represent decreases in decision-making costs and increases in external costs. For a decrease in X1, changes in the other directions would be suggested. As we have defined the four variables, the direction of change in X2, X3, and X4 would, in each case, be opposite to the change imposed on X1. Thus, we fill in the first row of matrix (15) with minus signs.
These signs indicate that, if the rule for the election of representatives to the assembly becomes more inclusive (if X1 increases), the basis of representation will tend to become somewhat more functional (X2 will be decreased), the degree of representation will tend to be decreased, that is, the assembly can be made smaller (X3 will be decreased), and the rule for decision-making in the assembly itself will tend to be made less inclusive (X4 will be decreased).
In a similar fashion we may examine the remaining rows in matrix (15). Look at the second row. Here we examine the effects on X1, X3, and X4 that might be predicted to result from a change imposed on X2, which measures the basis of representation. As the earlier discussion has suggested, a shift from a functional basis for representation to one that contains more randomized elements (an increase in X2) probably increases decision-making costs but decreases expected external costs. If this is correct, and if the variables are related in a compensating rather than a complementing way, the appropriate changes in the other variables will involve decreases in decision-making costs and increases in external costs. The signs in the second row of the matrix will also be negative. As the basis for representation in the assembly is increasingly randomized (as X2 is increased), the rational constitutional choice will tend to embody less inclusive rules for selecting representatives (lower values for X1), smaller representative assemblies (lower values for X3), and less inclusive rules for decision-making within the assembly itself (lower values for X4). Accordingly, two rows in the matrix can now be filled in, at least as to sign.
| (-) (-) (-) |
| (-) (-) (-) |
We now move to the third row, which relates to the effects on the “equilibrium” values for X1, X2, and X4 that are produced by independent changes imposed on X3, defined as the degree of representation. As X3 increases, that is, as direct democracy is approached, decision-making costs increase sharply, but, of course, expected external costs decrease. The rational individual, assumed to have some opportunity to choose values for the remaining variables, will tend to bear additional external costs (expected) at the other stages of the collective-decision process in order to “save” some decision-making costs (expected). He will tend to select some less inclusive rule for electing representatives (lower values for X1), a more functional basis for representation (lower values for X2), and some less inclusive rule for decision-making in the assembly (lower values for X4). The signs in the third row of the matrix are also negative.
| (-) (-) (-) |
| (-) (-) (-) |
| (-) (-) (-) |
The last row involves changes exogenously imposed on X4, the variable that describes the rules for making choices in the legislative assembly itself. For the same reasons as before, the signs of the symbols in the row will be negative. As the decision-making rule is made more inclusive (as X4 increases), rational constitutional choice should dictate a somewhat smaller assembly (lower values for X3), a somewhat more functional basis for representation (lower values for X2), and somewhat less inclusive rules for selecting representatives to the assembly (lower values for X1). The whole sign matrix may now be filled in.
| (-) (-) (-) |
| (-) (-) (-) |
| (-) (-) (-) |
| (-) (-) (-) |
If the relationships among the constitutional variables are those that we have assumed in constructing this matrix, the information contained in the matrix is of considerable importance.*50 The fact that all of the elements in the matrix should prove, on the basis of reasonable assumptions about the relationships among the variables, to have negative signs is relevant, methodologically, for our whole analysis of the constitutional-choice process.
The negative signs arise because we have been able to define each of the four constitutional variables in such a manner that an increase in each variable must involve higher decision-making costs and lower external costs—both of these cost elements being considered in an expected sense. This, in turn, depends on our ability to describe each variable (and others that might be potentially considered) in terms of these two basic cost functions. We conclude, therefore, that the highly abstract and simplified analytical model of Chapter 6 is far more powerful than might have been anticipated at first. At the outset the model may have appeared to be applicable only to direct democracy; but, because the other constitutional variables can be readily translated into the same functional variables, the basic analytical model can be employed as the general model for constitutional choice.*51 We have shown that the four constitutional variables introduced by representative government can be reduced in form to a single model that embodies the two essential cost functions.
This point may be clarified if we introduce an analogy with economic theory. Economists recognize that, in the real world, most business firms produce and market several products simultaneously. A full and complete analysis of the firm’s calculus would require an examination of many variables, and, conceptually, the fully rational firm must arrive at a determination of all of the variables under its control simultaneously. In spite of this recognition, economists can explain a great deal about the decision-making process of business firms by simplifying this process. By assuming that the firm produces and markets a single product, all of the analysis needed for a broad general understanding of the operation of business firms can be presented. Our model of the constitutional-choice process seems quite similar in this respect. In the real world there are many constitutional-institutional variables which the individual must rationally consider when he is given the opportunity of reflecting on the prospects of alternative political organizations. However, if our purpose is the relatively limited one of analyzing the essential decision-making processes through which all constitutional choices must be made, the simplified construction that we have emphasized seems quite helpful. Perhaps the absence of such models in the literature of political science is to be explained, in part at least, by an overconcentration on the apparent complexities of real-world political processes.

