The Common Sense of Political Economy
By Philip H. Wicksteed
Philip H. Wicksteed (1844-1927) wrote the
The Common Sense of Political Economy, Including a Study of the Human Basis of Economic Law (Macmillan and Co., Limited, St. Martin’s Street, London) in 1910.The edition presented here is the first edition, which was widely used as an economics textbook in classrooms in the United Kingdom and the United States, and probably elsewhere as well.A few corrections of obvious typos were made for this website edition. We also added occasional parentheses or square brackets to mathematical expressions for clarity [this was necessary in cases where the requirements of browsers to print fractions with a solidus (“/”) causes potential confusion when the entire fraction is to be multiplied by a subsequent factor:
e.g., to distinguish (1/2
x) versus (1/2)
x]. However, because the original edition was so internally consistent and carefully proofread, we have erred on the side of caution, allowing some typos to remain lest someone doing academic research wishes to follow up. We have changed some small caps to full caps for ease of using search engines.Editor
Library of Economics and Liberty
2000
First Pub. Date
1910
Publisher
London: Macmillan and Co.
Pub. Date
1910
Comments
1st edition.
Copyright
The text of this edition is in the public domain.
THE DIAGRAMMATIC EXPOSITION OF THE LAW OF RENT AND ITS IMPLICATIONS
CHAPTER VI
Summary.—
The current exposition of the law of rent, based on a diagram of “decreasing returns” to labour, for a constant of land, mistakes the characteristics of the constant for those of land. Hence many errors in nomenclature and in thought have arisen. It is equally easy and equally legitimate to represent the same facts in the form of a diagram with labour for the constant and land for the variable. This will shew that both rent and wages are shares in the product determined by marginal efficiency; and that when all the factors have received their share in this marginal distribution there is no surplus or residuum at all.
The roots of the error concerning the exceptional treatment of land, which we examined in the last chapter, go down far deeper than the point to which we have as yet traced them, and the process of extirpation cannot be completed without an elaborate examination of the current exposition of the theory of rent. We will therefore go on to the examination of the ordinary diagram given to illustrate both the supposed “law of decreasing returns” and the “law of rent” derived from it. In
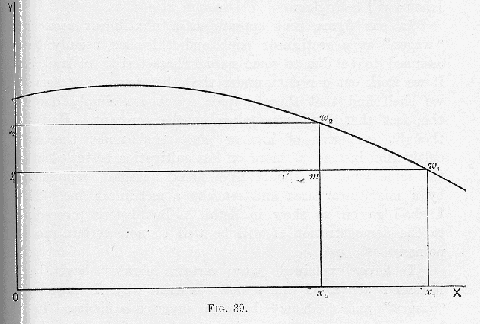 Fig. 39 increments of “labour” applied to a constant of land are reckoned along the axis of
Fig. 39 increments of “labour” applied to a constant of land are reckoned along the axis of
X, and rates of increment to the crop per unit increment of labour along the axis of
Y. The total yield for
Ox1 “labour” is
Orw1x1, and labour being rewarded at the rate of
x1w1 per unit receives the area
Ow1 altogether, the balance
y1rw1 being rent. If
Ox2 only had been applied to the same amount of land the total yield would have been the smaller area of
Orw2x2, but the reward of “labour”
per unit would have been higher, namely,
x2w2. Rent would only be
y2rw2, a smaller proportion of a smaller total. Thus decreasing returns to land per unit and increasing returns to “labour” per unit are read as we recede from the margin, and decreasing returns to “labour” per unit and increasing returns to land per unit as we advance from the origin. More labour bestowed on the same land means less land under the same labour. So we have these results: More labour on the same land or
less land under the same labour means a larger rent per unit of land and a less “wage” per unit of “labour”; whereas less labour on the same land or
more land under the same labour means a lower rent per unit of land and a higher “wage” per unit of “labour.” Those of the results just formulated which are directly illustrated in the figure are very familiar to all students of Political Economy, and familiarity has made them appear axiomatically true. But those of them which are just as explicitly contained in the data, but are only indirectly illustrated by the figure, and which have been italicised in the statement just made, are unfamiliar to most students of Political Economy, and may appear startling and perplexing, though they are absolutely identical with those expressed in the more familiar form and at once accepted as axiomatic.
Thus every one sees that if (after a certain point) more labour is applied to the same land the return to the land will be higher. But every one does not see that this is exactly the same as saying that after that point if more land is brought under the same “labour” the return to labour will be higher.
In our figure rent appears as a mixtilinear area and “wages” as a rectilinear one; and this has usually been assumed to be due to some special characteristic of land, but if we work out our data under the other form of statement we shall find that these graphic forms are simply due to the fact that land was taken as the constant. Had we thought in terms of less or more land under the same cultivation instead of more or less cultivation bestowed upon the same land, we should have found “wages” represented by a mixtilinear area and rent by a rectilinear one. This I shall go on to shew in detail. But before proceeding to the demonstration it will be well to note certain special points.
I have explained why certain phrases have been italicised above. I must now explain why I have put “wages” and “labour” between inverted commas. It is because labour is taken to include capital. In short, “labour” means all the factors of production except land. And “wages” means the remuneration of all these factors. To measure them all in one unit implies that they have all been reduced to a common denominator, and this must have been done on some such principle as that expounded in Book I. Chapter IX. It would be useless to attempt to express such a unit accurately every time we have occasion to speak of it. Even to call it a “unit of labour-and-capital-reduced-to-a-common-denominator” would be too cumbrous. To call it a unit of labour is in the highest degree dangerous; but the danger is reduced, though not altogether avoided, by systematically writing “labour” for this complex of factors, and “wages” for its remuneration. We must add that the distinction between “labour” in this sense and “land” is artificial and arbitrary; for all the land we ever deal with embodies capital, and so does “labour” as now defined.
We have next to note that the figure, and the argument that usually accompanies it, do not really give us any theory of rent at all. They assume our own law of remuneration in proportion to efficiency for all the other factors (tacitly reduced to a common denomination), and then simply tell us that whatever is not anything else is rent.
Further, we must note with extreme care that the number of units of “labour,”
Ox1 or
Ox2, applied to the constant of land, will be fixed by the alternatives open to land and “labour” respectively. “Labour” is devoted to, say, wheat-growing till the marginal return is only
x1w1, because it cannot find any more eligible alternative, and it is not devoted to it beyond that point, at a lower marginal significance, because it can find alternatives as eligible. And in like manner so much land and no more offers itself at a declining marginal significance to a given amount of wheat-growing “labour,” because it cannot find anything else better, but can find other things as good, to do with itself. So land will not come to a man unless he offers it as good terms as it can get anyway else, and men will not come to land unless it offers them as good terms as they can get anyway else. The quantities
Ox1,
x1w1,
y1rw1, are determined by the general conditions of industry and the markets; and if under conditions which would justify these proportions an individual should choose to take land and work on it at the rate represented by
Ox2, instead of earning
Ow2 and paying
y2rw2 in rent, he would find that out of his total crop of
Ow2 he would have to pay a rent of
y1rw1, and would only have
Om minus the mixtilinear triangle
w2mw1 for himself. If rent were at the rate of
y2rw2, and “wages” at
x2w2, it would be because more eligible alternatives had been opened to “labour,” or a more abundant supply of land had become available to it as against the conditions that determined
y1rw1 and
Ow1. It should be noted incidentally that any such change would be sure to affect the internal constitution of the complex unit of what we have called “labour”; it would not act upon interest on capital and wages for every different grade and character of work, for instance, in exactly the same proportion.
Lastly, we may note that the figure deals with yield per unit of land of a given quality, as it is plied with more and more “labour.” It takes no account of different grades of land, each of which would present a curve of different form. Neither does the figure take account of the different conditions that might prevail on larger and smaller holdings.
With reservations, the nature of which will presently appear, as to the general form of the curve, we may now proceed to the detailed demonstration promised on page 552. It will be well to begin from the beginning and build up our curves step by step.
Suppose a man holds 50 acres of land and bestows 3000 hours’ personal work upon it in the course of the year, backed by tools and apparatus of every kind, stock, seed, manure and so forth, and also hired labour. An hour’s labour will in this case be a mere symbol of an aggregate of factors of production, of defined magnitude, expressed under a common denominator, and will mean “the totality of the applications and combinations which may be supposed to accompany, or to be included in, the expenditure of an hour’s work on the land by the tenant.” Let us suppose that the crop is about equivalent to 5 quarters (or 1280 quarts) of wheat per acre. For convenience of subsequent operations we will take it at 1260 quarts, and this would be 630 quarts per half-acre. Thirty “hours” a year will be devoted to each half-acre. So the crop will be at the rate of 21 quarts per “hour” expended. We will take this as our starting-point. But it will be convenient to take a smaller unit of land than the acre or half-acre. Let it be the twentieth of a rood (which would be two poles), or the fortieth of a half-acre. The selection of the unit is determined merely with a view to diagrammatic convenience. Then our supposition will be: Land cultivated to the point of 60 “hours” to the acre yields the equivalent of 1260 quarts of wheat per acre, which is at the rate of 21 quarts per hour, or 15.75 per (two-pole) unit of land.
| The scale of |
| 1260 quarts per 80 land-units under 60 hours’ cultivation |
| is the scale of |
| 630 quarts per 40 land units under 30 hours’ cultivation, |
| and the yield is at the rate of |
| 630 ÷ 30 = 21 quarts per hour, or |
| 630 ÷ 40 = 15.75 quarts per land-unit. |
Here the reader must note carefully that these rates per unit of land and labour are not shares which fall to each of the factors, nor estimates of the value of their respective contributions. They simply indicate the ratio of the gross crop to the land or to the labour, taken severally. Yield per unit of land is a familiar conception. Yield per unit of labour is equally important for our present investigation, and the reader must try to make himself equally familiar with it.
Let us now suppose that if the man only cultivated at the ratio of 25 “hours” per half-acre his crop would be at the rate of 531.40 instead of 630.
*47 Here note that we are imagining our cultivation to be less intensive than on the first supposition; that is to say, the cultivation or “labour” is spread thinner on the land. This we may think of in terms either of the unit of land having less labour spread on it, or of the unit of labour being spread over more land. Thus, if we pass from 30 “hours” on 40 land-units to 25 “hours” on 40 land-units, we get the same ratio (5 to 8) which we should have got had we passed from 30 on 40 to 30 on 48 (5 to 8 again); but of course the total crop on 48 land-units under 30 “hours’ “; cultivation will be greater by a fifth than that on 40 land-units under 25 hours’ cultivation.
Thus if, as we have (arbitrarily) supposed, the crop on 40 land under 25 labour is 531.40 quarts, it follows that the crop on 48 land under 30 labour will be 637.68 quarts (six-fifths of the other); and whichever way we measure it we shall have a yield of 13.285 quarts per unit of land and of 21.256 quarts per unit of labour.
We may tabulate these results:—
| Quarts per “hour.” |
Quarts per land-unit. |
||
| 30 to 40 | gives a yield of | 21 | 15.75 |
| 25 to 40 | |||
| or | 21.256 | 13.285 | |
| 30 to 48 |
Thus as we pass from 25 to 30 units of cultivation on 40 units of land we have decreasing returns to labour, but increasing returns to land. To say that we have a decreasing or increasing “total yield” would have no sense unless we had established some common denominator (pecuniary or other) under which we could express land or labour indifferently, or both collectively. This lies outside our present inquiry; and we see that “increasing” and “decreasing” returns, from our present point of view, are merely relative terms and may be applied to the same phenomenon simultaneously according to whether we are speaking of land or of “labour.” To this important conception we will presently return, but meanwhile we are to follow our investigations along another track.
Our hypothesis is that at 30 “labour” to 40 land we have a crop of 630; so that we may call this the return either to 30 “labour” or to 40 land, on the supposition of the ratio of 3 to 4. When we alter the ratio to 5 to 8, we may keep either 40 land (with 25 “labour” spread on it), or keep the 30 “labour” and spread it over 48 land. In the one case we shall have a crop of 531.40 instead of 630, and in the other a crop of 637.68 instead of 630; that is to say, if we spread so much less labour on the same land we shall decrease the yield
to the land by 98.60 quarts, and if we bring so much extra land under the same “labour” we shall increase the yield
to the “labour” by 7.68 quarts.
We may now begin to plot out our results on
 Fig. 40. In (
Fig. 40. In (
a) we may assume that the half-acre (40 of our land-units) is constant. We mark along the axis of
X the number of “hours” per half-acre put in annually, and on the axis of
Y rates of yield measured in quarts, so that the crop per half-acre, for any ratio between land and labour, will be represented by areas in which every small square is a quart. In (
b) we will take 30 “hours” of cultivation per annum as our constant, and will measure along the axis of
X the units of land (twentieths of a rood) over which it is spread. The meaning of the units on the axis of
Y will still be rates of yield measured in quarts, and areas will represent the crop per 30 “hours’ “; cultivation, for any ratio between land and “labour.” In (
a) as we advance from 25 “hours” to 30 we secure by hypothesis an addition of 98.60 quarts per half-acre, or if we move in the opposite direction, from 30 to 25, a diminution of that amount. This may be plotted on (
a) by erecting a rectangle of an altitude 19.72 on the base line between 25 and 30. This means that, land remaining constant, the addition or withdrawal of these 5 hours per half-acre will make the difference we have assumed in the crop. But, as we have seen, to pass from 30 to 25 on (
a) is equivalent to passing from 40 to 48 on (
b), since each of them means changing the ratio of 3 : 4 into that of 5 : 8; and the effect of this change is to increase the yield to 30 “hours” of labour by 7.68. In (
b), on the base line between 40 and 48, we must therefore erect a rectangle of area 7.68 or altitude 0.96, which means that, “labour” remaining constant, the addition or subtraction of these eight land-units will make a difference of 7.68 quarts in the crop.
Note that movement towards the origin in (
a) corresponds to movement away from it in (
b). We may either start with the ratio 3 : 4 and move to the left in (
a) and to the right in (
b), or we may start with the ratio 5 : 8 and move to the left in (
b) and to the right in (
a). That is to say, our data imply that if we increase the number of “hours” spread over the same land we shall increase the yield per unit of land and decrease the yield per unit of “labour,” whereas if we bring more land under the same output of cultivating labour we shall increase the yield per unit of “labour” and decrease the yield per unit of land.
Let us now change the ratio of 3 : 4 in the contrary sense. Let us suppose (as an arbitrary datum) that a ratio of 7 : 8, that is to say, of 35 “labour” to 40 land, or 30 “labour” to 34.286 land, would yield a crop of 705.98 per half-acre, or six-sevenths of this, viz. 605.13 per 30 “hours.” This would mean that the difference made to the crop by the addition or subtraction of these five “hours” on 40 land-units is 75.98, and may be represented on (
a) by a rectangle on the base line between 30 and 35 with an altitude of 15.20; whereas the difference made by the addition or subtraction of these 5.714 land-units under 30 “hours” of cultivation is 24.87, and will be represented on (
b) by a rectangle whose base is the line between 34.286 and 40 on the abscissa, and its altitude 4.35.
We can now tabulate and extend our results. If we start with the rectangle on the left in (
a) and move to the right, and with the corresponding rectangle on the right in (
b) and move to the left, we shall have a series of increments to record on (
a), and of decrements to record on (
b). But the figures may be read either way, and if we read (
b) towards the right and (
a) towards the left we should have increments to record on (
b) and decrements on (
a). We shall therefore not mark positive or negative signs on our table; for if we read it down the differences in column 6 will be positive and those in column 7 negative, and if we read it up it will be the other way, and either reading is equally legitimate.
| Ratio of “Hours” to Land-units. | “Hours” to Constant of 40 Land-units. | Land-units to Constant of 30 “Hours.” | Crop to Constant of Land (on Arbitrary Hypothesis). | Crop to Constant of “Labour” (on same Hypothesis). | Difference in Yield to Constant of Land. | Difference in Yield to Constant of “Labour.” | Height of Rectangle on ( a). |
Height of Rectangle on ( b). |
| 5 : 8 | 25 | 48 | 531.40 | 637.68 | ||||
| 98.60 | 7.68 | 19.72 | 0.96 | |||||
| 3 : 4 | 30 | 40 | 630 | 630 | ||||
| 75.98 | 24.87 | 15.20 | 4.35 | |||||
| 7 : 8 | 35 | 34.286 | 705.98 | 605.13 | ||||
| 53.18 | 35.76 | 10.64 | 8.34 | |||||
| 1 : 1 | 40 | 30 | 759.16 | 569.37 | ||||
| 31.85 | 42.03 | 6.37 | 12.61 | |||||
| 9 : 8 | 45 | 26.667 | 791.01 | 527.34 | ||||
| 12.99 | 44.94 | 2.60 | 16.85 | |||||
| 5 : 4 | 50 | 24 | 804 | 482.40 |
Now, as the effect of increasing the labour bestowed upon the same land in the one case, or increasing the land brought under the same expenditure of cultivation in the other, will obviously be continuous, we may trace curves on the principle fully explained on page 447, which in the case of (
a) will correspond to the ordinary curve given to illustrate rent in the books, and in the case of (
b) will be the complementary curve in which labour is supposed to be constant. Thus, for any abscissa on (
a) the corresponding ordinate will mark the marginal efficiency of labour per hour, at that point, in increasing the yield to a constant of half an acre of land (40 land-units); and for any abscissa on (
b) the ordinate will represent the marginal efficiency of land per unit, at that point, in increasing the yield to 30 “hours” of labour.
What we have got in (
a), therefore, is a portion of the familiar rent curve. It shows us the “decreasing returns” to “labour” as successive increments or doses are applied to the same piece of land; and since “labour” is remunerated at the rate of its marginal efficiency, the rectangle of the ordinate multiplied by the abscissa, that is to say, the rectangle contained by the curve, is the total amount that would be paid in “wages.” There remains the rest of the crop for rent; and if the curve were completed, that would be represented by the mixtilinear area above the rectangle.
This last point may easily be established. The land would produce no crop at all unless some labour were expended on it. Thus, if we start with the crop for
x “hours” per land-constant, and successively account for, and register as an area, the part of the crop dependent on the difference between
x and (
x – 1) “hours,” the part dependent on the difference between (
x – 1) and (
x – 2), and so on, up to the part dependent on the difference between 1 and 0, we shall have accounted for the whole crop. Now our curve is constructed precisely on these principles. Over each successive base it bounds an area which represents, by construction, the part of the crop for which the corresponding portion of the abscissa is responsible. Thus, if we had completed it, it would account for the whole crop. For example, at the ratio of 3 “labour” to 4 land, or 30 “labour” to 40 land, we take the abscissa 30 on (
a) and read 17.50 as the marginal significance of “labour” per hour. If this represented a state of equilibrium, 17.50 × 30 = 525 would be the amount of the crop that would fall to “labour,” and the rest would measure the rent of half an acre.
In (
b) we should have a portion of a precisely analogous curve shewing the “decreasing returns” to land as successive increments are brought under the same amount of “labour”; and since land will also be remunerated at the rate of its marginal efficiency the rectangle contained by the curve is the total paid for rent. The rest of the crop will remain for “wages.” The point 40 on the abscissa of (
b) corresponds to the point 30 in (
a). Reading the ordinate for the abscissa we find it to be 2.625. The rent then will be 40 × 2.625 = 105, and the rest of the crop will be the “wages” of thirty “hours” of labour.
If our curves have been accurately drawn and correctly read these results must coincide. And so they do. For returning to page 554, where the total crop for 30 “hours” bestowed on 40 land-units is taken at 630 quarts, we find from (
a) that wages will be at 30 × 17.5 = 525, and from (
b) that rent will be at 40 × 2.625 = 105. And 525 + 105 = 630.
Let it be clearly understood that all we have proved is that the same data may be diagrammatically expressed in two different ways; and that these two representations, if correctly made, will be consistent. That our sum comes out right proves nothing; and if it came out wrong it would disprove nothing. The curves are to be drawn in accordance with the calculations, and they can be calculated more accurately than they can be read. They illustrate the calculations; but they do not prove them to be correct. The calculations, as legitimate inferences from the data, must stand or fall on their own merits. The curves simply illustrate the relation in which the different inferences stand both to each other and to current (or recently current) economic teaching.
The essential and all-important point of the demonstration, up to this point, is that in the ordinary diagrams rent is set forth as a mixtilinear and “wages” as a rectangular area, not because there is any inherent appropriateness in these geometrical forms as representatives severally of the respective industrial factors, but simply because return to the constant, whatever it happens to be, will always come out as a mixtilinear area, and that to the variable as a rectangular one. And whether a distributive share is represented as a mixtilinear or a rectangular area, it is the same quantity and it is marginally determined.
This will become still clearer if we plot the total crop (for each ratio of land and “labour”) to 40 land-units and to 30 “hours” respectively, in conjunction with the marginal returns to “labour” and to “land.” I must refer my readers to the short mathematical treatise already mentioned
*48 for the detailed justification of the general form of the curves which our data imply; but it is sufficiently obvious that the form of figure usually given (as in Fig. 39) is an exceedingly crude representation of the facts. The more careful writers always state that the law of diminishing returns will only come in “after a certain point,” and assume that when we are near the origin increments of labour will produce more than a proportionate increase in the product. Further, it is clear that if I were to distribute a few hours’ labour over many acres of land (really distributing it over the whole, not selecting a portion of it), I should produce no appreciable effect at all. The difference between giving so much labour and no labour would not be perceptible. If, on the other hand, I were already giving 300 days’ work to a holding of 40 acres, every extra hour of work would produce an appreciable result. Thus I have attempted, in the work referred to, to shew that our curves will pass through the origin, will rise for a time, and then decline. Our data have hitherto been assumed in accordance with this theory, and we may now extend them so as to carry our data for (
a) back to the origin in one direction, and some way farther to the right than it has yet reached in the other.
We will assume, then, the following data, some of which have been already tabulated, the rest being now introduced for the first time:—
*49
| TABLE I.—Land-Constant at ½ Acre (40 Units). | ||||
| Ratio of Labour to Land. | “Hours” of Cultivation per Constant of Land. | Crop per Constant of Land (Assumed). | Total Crop per Unit of Land (Derived). | Total Crop per Unit of “Labour” (Derived). |
| 1 : 8 | 5 | 46.26 | 1.16 | 9.25 |
| 1 : 4 | 10 | 152.36 | 3.81 | 15.24 |
| 3 : 8 | 15 | 282.24 | 7.06 | 18.82 |
| 1 : 2 | 20 | 413.08 | 10.33 | 20.65 |
| 5 : 8 | 25 | 531.40 | 13.28 | 21.26 |
| 3 : 4 | 30 | 630.00 | 15.75 | 21.00 |
| 7 : 8 | 35 | 705.98 | 17.65 | 20.17 |
| 1 : 1 | 40 | 759.16 | 18.98 | 18.98 |
| 9 : 8 | 45 | 791.01 | 19.78 | 17.58 |
| 5 : 4 | 50 | 804.00 | 20.10 | 16.08 |
| 11 : 8 | 55 | 800.91 | 20.02 | 14.56 |
| 3 : 2 | 60 | 784.74 | 19.62 | 13.08 |
| 13 : 8 | 65 | 758.22 | 18.96 | 11.66 |
| 7 : 4 | 70 | 724.01 | 18.10 | 10.34 |
If we take the figures in the second column as a series of abscissas and those in the last column as the corresponding ordinates, we shall have a series of points in a curve the rectangle contained in which gives the total crop per half-acre (40 units) at any ratio of land to labour. And if we add the curve of marginal significance of “labour” applied to a constant of 40 units of land, we shall have on our
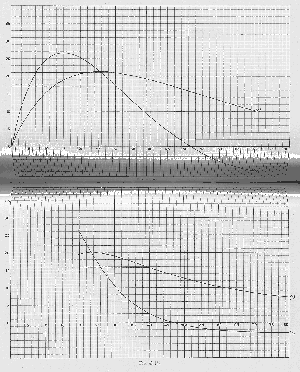 Fig. 41 (
Fig. 41 (
a) one curve
c (which stands for “crop”) containing the rectangle of the total crop per 40 units of land, and another curve
w (which stands for “wages”) containing the rectangle of the share of labour in that total. The first of these rectangles minus the second will obviously represent the share of land, also as a rectangle. And this last rectangle will be equal to the total area of curve
w minus the rectangle it contains. If we divide it by 40 we shall have the figure in the last column but one of our table.
But the assumed data of Table I. can be presented in Table II. for a constant of 30 “hours” and a variable of land-units. We have taken our points on the abscissa of (
a) at uniform intervals of 5 units and assumed data to match them. The corresponding intervals on (
b), being reciprocals will not be uniform. It would, of course, have been equally easy to have gone the other way about, so the regularity in one case and the irregularity in the other has no theoretical importance. We will tabulate for 30 “hours’ “; constant the data corresponding to the abscissas from 60 to 15 in Table I.
| TABLE II.—For 30 “Hours’ ” Constant. | ||||
| Ratio of Labour to Land. | Land. | Crop per Constant of “Labour” (Derived). |
Crop per Unit of “Labour” (Derived). |
Crop per Unit of Land (Derived). |
| 3 : 2 | 20 | 392.37 | 13.08 | 19.62 |
| 11 : 8 | 21.818 | 436.86 | 14.56 | 20.02 |
| 5 : 4 | 24 | 482.40 | 16.08 | 20.10 |
| 9 : 8 | 26.667 | 527.34 | 17.58 | 19.78 |
| 1 : 1 | 30 | 569.37 | 18.98 | 18.98 |
| 7 : 8 | 34.286 | 605.13 | 20.17 | 17.65 |
| 3 : 4 | 40 | 630.00 | 21.00 | 15.75 |
| 5 : 8 | 48 | 637.68 | 21.26 | 13.28 |
| 1 : 2 | 60 | 619.62 | 20.96 | 10.33 |
| 3 : 8 | 80 | 564.48 | 18.82 | 7.06 |
Here again, by taking the figures in the second row as abscissas and those in the last row as the corresponding ordinates, we shall obtain a series of points on a curve
c, Fig. 41 (
b), the rectangle in which gives the total return to 30 “hours’ “; cultivation applied to the amount of land marked by the abscissa; and if we add the curve of marginal significance of land, we shall have in (
b) a curve
c (crop) containing the rectangle of the total crop to 30 “hours,” and a curve
r (“rent”) containing the rectangle of the share of land in that total. The first of these rectangles minus the second will represent the share of “labour,” also as a rectangle. And this last rectangle will be equal to the total area of curve
r minus the rectangle it contains. If we divide it by 30 we shall have the figure in the last column but one of Table II.
Thus the readings of (
a) and (
b), either in Fig. 40 or Fig. 41, will give absolutely identical results, if the figures are correctly and consistently drawn. The reader will be able to check this roughly by reading the curves for any two corresponding points that lie between the tabulated points. For example, on (
a) take the rate of 35 “labour” to 40 land. This gives us 12.9 for wages per hour; and 7.3 × 35 for the rent of 40 units of land, or about 6.4 per unit. Now 35 to 40 is 30 to 34.3. Therefore the corresponding point on (
b) will have the abscissa 34.3. If we read the ordinates we find that rent is about 6.4 and the wages 11.3 × 34.3 for 30 hours, or 12.9 per hour.
We have now thoroughly established the important conclusion that there is no special propriety in regarding rent as a residual share in the product, nor is there any special or necessary appropriateness in representing rent diagrammatically as a mixtilinear area, in contrast to the representation of wages, for example, as a rectilinear area. But the mistaken conceptions now dissipated have led to what I cannot but regard as disastrous confusions both in thought and nomenclature which may long impede the progress of Economics. It has been assumed, in the first place, that every economic quantity that presents itself graphically, under any treatment, in the form of a mixtilinear area has some specific analogy to rent. And here we may note that what is known as the “Ricardian” law of rent may be presented in this same form. Thus a diagram of the form in Fig. 39 (page 551) might be regarded not as shewing the relation between marginal-return-per-unit-of-labour-and-capital and ratio-of-labour-and-capital-to-land, but as an arrangement of the several units of labour and capital employed in the wheat industry, referred to the varying fertility of the land to which they are applied. We should then have the mixtilinear area representing the excess of the yield of the more fertile over the yield of the least fertile land under cultivation. The Ricardian theory of rent usually (though quite unnecessarily) assumes that the least fertile land will bear no rent at all, and in that case the mixtilinear area would represent the whole rent; otherwise it would represent the excess of rent over a minimum. Now, if you take a number of persons who possess different talents and arrange them in the order of the marginal value to the community of the exercise of their talents, you will have near the origin an individual the product of whose efforts per annum is relatively high, and as you go forward you will come to individuals the exercise of whose talents produces a smaller and smaller pecuniary return. If we draw a line on the level of the return to the efforts of the least efficient of the men in question, the area above it will represent the excess over that minimum return that accrues to the more able individuals; and simply because this is a curvilinear figure the revenue it represents has actually been called “rent of ability.”
It is clear that at this rate any excess in the value of one article above another that is nominally the same would be entitled to the name of “rent.” Thus, if a pound of one kind of manure produces the same result as two pounds of another, and so forth, you might register pounds of the different manures, in order of their efficiency, along the axis of
X, and treat the excess of efficiency of a pound of the one over a pound of the other as “rent of superior efficiency.” Indeed, if any two things could perform the same function, but one of them could perform more of it than the other, you might regard the excess of the price of one over the price of the other as a case of “rent.” And in very truth that is all that the Ricardian law of rent amounts to. If two pieces of land can each of them yield wheat to labour and capital, but one yields more wheat than the other, the value of that land will be proportionately higher, just as the value of an apple-tree that bore an average of two hundred apples of given quality per annum would be higher than that of one that only bore an average of one hundred and fifty of the same quality. In fact the Ricardian law of rent is nothing whatever but a statement that the better article commands an advanced price in proportion to its betterness. The introduction of the hypothesis that the lowest quality of the article is to be had for nothing would make the whole price of the better article due to its “betterness.” If there is no such gratuitous supply, then only the excess of the price of the more expensive article in the market would be due to its “betterness,” and the rest to its “goodness” up to the point of lowest goodness in the market.
Again, reverting to our former interpretation of the figure (waiving all scruples as to the course of the curve in the neighbourhood of the origin), and bearing in mind that the form of the mixtilinear area is determined simply by the fact that land is constant, we shall see that by representing any other factor as constant we shall obtain a representation of it as a mixtilinear area. Thus, in all the individual and communal curves which represent the declining marginal significance of successive supplies of any commodity, we may regard the
psyche or sensitive organism as the constant, and the areas as psychic. If the sensitive organism, or body of sensitive organisms, remains constant, successive increments of the provocative or stimulus will, after a certain point, produce decreasing revenues or volumes of the experience in question, and we shall therefore have the mixtilinear area representing an excess in the experience provoked by the earlier over those provoked by the marginal increments. When students perceived this they promptly dubbed that excess “consumer’s rent.”
But misleading as these uses of “rent” appear to me to be, they constitute but a small part of the evil that we have to deal with.
We have seen that the figure constructed on the hypothesis of land being constant, and labour and capital variable, may equally well be regarded as an illustration of the Ricardian theory of rent when associated, as it usually is, with the hypothesis of “no-rent” land being under cultivation. The general attitude of mind with regard to rent that results from all this may be thus described:—Rent is a residuum which is determined by the subtraction of the shares of the other factors of production, and what those shares are is determined by the remuneration they can secure on “no-rent” land—that is to say at the margin of cultivation.
We may notice in passing that this treatment of rent as a residuum incidentally stultifies the claim of the current economic science to have established a “law of rent” at all. For if rent is simply what is left when the other factors have been satisfied, we have not established a law of rent, but have assumed that we know how to determine the shares of everything except land, and then simply stated that what is not anything else is rent. If we start from
x =
a +
b +
c + etc., we cannot determine
a simply by the equation
a =
x –
b –
c – etc., unless we have independently determined the values of
b, c, etc. Thus, what is usually given as a derivation of the law of rent from the law of decreasing efficiency of successive doses of labour and capital on the same land is really an assumption that every other factor of production obeys the law of marginal efficiency which we have taken as our guide to the whole theory of distribution. Instead of elaborating a theory of rent the current exposition tacitly assumes a (correct) theory with reference to everything except land, and then claims that no theory at all is necessary for land. But our elaborate examination has shewn that the diagrammatic exposition strictly involves the conclusion that that same law really applies to land just as much as to the other factors. In truth, then, the mixtilinear area represents rent, not because it is all that is left when the other claimants have been satisfied, but because it represents the marginal efficiency of land, and would be represented by an ordinate if we had taken labour as the constant, just as labour is represented by an ordinate when we take land as the constant.
But we are concerned at present not with the inconsistencies already involved in regarding rent as a residuum, but with the further conclusions that have flowed from it. If rent, it is argued, is a surplus or residuum which can be arrived at by deducting the remuneration of the other agents, as measured by the return to them on marginal or “no-rent” land, why should not profits be regarded as the residuum or surplus to be arrived at by deducting the remuneration of other agents, as measured by their returns in a marginal or “no-profit” business? And when, by these or similar processes, we have arrived at satisfactory “laws” which determine rent, profits, and so forth, surely we can determine wages (as General Walker did) by making them, too, a residuum when the other factors have been paid off. It is clear that all such attempts are based on the system of equations
a =
x –
b –
c – etc.,
b =
x –
a –
c – etc.,
c =
x –
a –
b – etc., and so on, none of which adds anything to the original datum
x =
a +
b +
c + etc., but each of which assumes that data have been independently obtained, with respect to all agents except that one to which it specially refers.
Nor is this the last or the worst of it. The reader will have noticed that the use of ” margin” or “marginal” which we are now examining is quite different from that in which we have defined it on page 40
sq. and used it throughout this work. “Marginal land,” for instance, or “marginal ability,” in this connection, is not land or ability considered with reference to the volume of the supply, at the margin of which it is added or subtracted, but land or ability of the lowest intrinsic quality which is devoted to the industry in question. And the marginal conditions are not the conditions determined throughout the industry by the “margin” in our sense, that is to say, by the marginal significance of adding or subtracting a small increment, but are certain specified conditions applying to the production of specified units of the product. On this conception of margins many writers have conceived of one distributive category after another as consisting of an actually existing “surplus,” mounting backwards towards the origin from the “margin,” and constituting a great reservoir untapped by marginal distribution; and bewildered and bewildering attempts have been made to get at the marginal (least efficient) man working with the marginal (least efficient or least abundant) capital on the marginal (least efficient) land, and to calculate everything backwards from this point. But it must now be clear to the reader that all such attempts are based either on the mere arrangement of units on the abscissa in the order of their efficiency, which neither illustrates, nor proves anything except that the better article commands the better price, or else are based on a misunderstanding of the geometrical form necessarily assumed by the area that represents the constant, whatever it may happen to be, in a diagram constructed on the principles of Fig. 39 (page 551). The ambiguous use of the term “margin” has obviously added to the confusion. We now see once for all that the marginal distribution in our sense (that is to say, the distribution of the product amongst the claimants in proportion to the significance of the addition or withdrawal of a small increment, at the margin determined by the present supply), exhausts the whole product. The curvilinear area represents a margin just as much as the linear ordinate does, and may just as well be represented in the same geometrical form.
In our phraseology a unit “at the margin of
x” is not contrasted with the other units in the group, which are in some way superior to it. All the units in the group are at the margin. The distinction is not between the
x units of the group severally, but between the significance of each of a number of qualitatively indistinguishable units when forming one of a group of
x and when forming one of a group of
x + 1. The one use of the term implies qualitative differences, the other presupposes qualitative identity, within the group. In our sense of the term, therefore, all the units of every group are always marginal units, whatever the margin may be; and therefore, naturally, the marginal distribution accounts for the whole product.
It is open to any one to examine or to dispute the ethical or social claim of any factor of production to a share, in accordance with its marginal significance, or to argue that there is no industrial necessity to allow such a claim; but it is not open to any one who understands the facts to argue that when, by a marginal distribution, every factor, reduced to the common term (on the principles of equivalence of marginal significance expounded in Book I. pages 368
sq.), has been satisfied, there remains any residuum or surplus whatever to be divided or appropriated. The vague and fervid visions of this unappropriated reserve, ruling upward as we recede from the marginal distribution, must be banished for ever to the limbo of ghostly fancies.
Before we bid farewell to the current or recently current expositions of the law of rent, we have still to notice one curious and instructive point. There is no connection whatever between the definition of rent given by the economists and the demonstrations by which they seek to determine its amount; for the economists first carefully define land as the primitive and inalienable properties of the soil, and explain that any ordinary piece of agricultural land is, to an indefinite extent, not land at all, but capital; and then proceed to examine the law of rent (almost invariably drawing their illustrations from agricultural land) on principles that take no account whatever of this distinction; for, as far as concerns the “Ricardian” law, it is clear that if one man commands a rich alluvial soil, and another man commands soil which by drainage, permanent manuring, and other devices, has been made equally desirable, both the one and the other, and both in equal degree, will pay a higher rent than they would pay for unmanipulated moorland which it is just worth while for some one to cultivate. And again (to take the law of rent as expounded in connection with the principle of “decreasing returns”), whether the land which we rent has been made what it is by mixing marl with the original soil, by drainage, or by other deliberate process, or is what it is by virtue of its original properties, or has become valuable because of the opening of a railway line or the building of a number of houses in the neighbourhood, in any case it will be cultivated more or less intensively on exactly the same principles. The law of rent, then, as expounded by the economists, has no connection with land as defined by them, but connects itself readily enough with land in the popular sense, which is an amalgam of economic land and economic capital.
There is nothing surprising in this, for we have seen over and over again that it is impossible to draw the line either between land as a primitive gift of nature and land as embodying capital or the results of human effort, or between a change in the value of a piece of land caused by something that has been done to it and that caused by changes that have taken place elsewhere. And, finally, since we know that land and capital are remunerated on one identical principle, in conformity with their marginal efficiency, we can see that the attempt to distinguish accurately between them is as unnecessary as it is hopeless.
Indeed it may be roughly said that everything that we read in Economic books as to the pure theory of distribution, whether it refers to wages, interest, rent, or profit, is either false when asserted of the category under discussion, or else true of all the others as well.
x2e
-(7/180)x, in which
x stands for the number of “hours” put in per annum per 40 land-units. The corresponding formulæ for the pair of curves on Fig. 41(
a), page 566, will naturally be 2.248
xe-(7/180)x for the curve containing the rectangle, and 2.248[2 – (7/180)
x]
xe-(7/180)x for the curve the integral of which equals the rectangle.
