The Common Sense of Political Economy
By Philip H. Wicksteed
Philip H. Wicksteed (1844-1927) wrote the
The Common Sense of Political Economy, Including a Study of the Human Basis of Economic Law (Macmillan and Co., Limited, St. Martin’s Street, London) in 1910.The edition presented here is the first edition, which was widely used as an economics textbook in classrooms in the United Kingdom and the United States, and probably elsewhere as well.A few corrections of obvious typos were made for this website edition. We also added occasional parentheses or square brackets to mathematical expressions for clarity [this was necessary in cases where the requirements of browsers to print fractions with a solidus (“/”) causes potential confusion when the entire fraction is to be multiplied by a subsequent factor:
e.g., to distinguish (1/2
x) versus (1/2)
x]. However, because the original edition was so internally consistent and carefully proofread, we have erred on the side of caution, allowing some typos to remain lest someone doing academic research wishes to follow up. We have changed some small caps to full caps for ease of using search engines.Editor
Library of Economics and Liberty
2000
First Pub. Date
1910
Publisher
London: Macmillan and Co.
Pub. Date
1910
Comments
1st edition.
Copyright
The text of this edition is in the public domain.
MARGINS. DIMINISHING PSYCHIC RETURNS
CHAPTER II
Summary.—
The significance of any given addition to our supply of a commodity or other object of desire declines as the supply increases. Its significance for any given supply is called its marginal significance. This marginal significance therefore rises or falls as the supply itself is contracted or expanded, and the margin drawn back or advanced. If there is a market price for any commodity, we supply ourselves with it till its marginal significance sinks to its market price; and seeing that all the early increments of supply have a higher value than that at the margin, though all are bought at the market price, it follows that the satisfactions we secure are worth more than the price we pay for them. Only at the margin is there a coincidence between the thing gained and the price paid for it. In more general terms, if we can exchange things for each other or choose between them, on certain terms, then we can increase our supply of the more valued thing at the expense of the other, thereby lowering the marginal significance of one and raising that of the other, till their significance coincides with the terms on which they are obtainable as alternatives. When this point is reached there is equilibrium; and successful administration of resources consists in establishing and maintaining such equilibrium. In making these exchanges or selections we are guided by the anticipated or estimated values of the things with which we are dealing, and if we make mistakes and fail to secure the marginal coincidence between what we have got and the terms on which we got it, the price we mistakenly paid does not affect the value of the thing for which we paid it. The scale on which all objects of desire are arranged and graded in a man’s mind, spoken of in the last chapter, must be thought of as a scale of marginal values.
The present chapter will be devoted to the further examination of the conception of the “relative scale,” and to the introduction, in connection with it, of a second great principle which combines with that of price to control the distribution of our resources.
We have seen that the skilful marketer has a portion of her scale of preferences definitely and even minutely present in her consciousness as she enters the market. She knows with considerable nicety the terms on which this or that alternative purchase is preferable, and the immensely complex system of combinations which can be commanded by the money she has to spend is fairly well under her ken. She may therefore come out of the marketplace having done something like the best that was possible with her money. But in order for this result to represent the most effective administration of her resources in general for all the purposes of her life, other opportunities than those of the market in which she actually stood must also have been present in her mind with adequate preciseness; for her total expenditure in the market-place is not rigidly fixed in advance. It is related to her expenditure on other things (furniture, clothes, education, literature, holidays, etc.), and should be kept in close and continuous connection with it. And just as her expenditure on provisions is affected by the price of all these other things, so likewise her expenditure on them is affected by the price of provisions. The price of one or many of the commodities in the market may be considerably different from what she expected. If she finds that she can fill her basket for less than she expected she may feel at liberty to buy something else that she would not otherwise have allowed herself; and if prices are so high that the money she had meant to spend will make too poor a provision she must cast about for some saving elsewhere to enable her to spend a little more in the market-place. So when she learns the prices at the stalls, she may find she “can get that scarf for Bob after all,” or, on the contrary,that with things at such prices, she “must put off binding
Grimm’s Fairy Tales a little longer.” The ideal marketer therefore will have in her mind, as she enters the market, a perfectly clear and precise realisation of that portion of her scale of preferences which is immediately concerned, while those portions of it which are adjacent and bear most directly and closely upon it will be within easy reach; and the whole range will be subconsciously present in what psychologists call “the fringe.” So much for recapitulation.
We may now go on to the next great step in advance in our analysis of the scale of preferences or relative estimates. We have noted incidentally more than once that the question may arise not only, for example, whether to buy any new potatoes at all, but also how many to buy. Suppose the usual consumption of potatoes in a family is about 4 lbs. a day (2 stone a week), and sound old potatoes are about ½d. the lb. If new potatoes are 2d. the housewife may determine to buy 2 lbs. that week, for a treat, reckoning that they will go once round on Sunday, the second dish to be of old potatoes as usual, or if that takes too much trouble the second dish to be dispensed with. If they are 1½d. a lb. she may buy 4 lbs. and have all new potatoes on Sunday, or one dish on Sunday and one on some other day in the week; or she may buy enough for the birthday dinner of one of the children. But when new potatoes come down to a penny she will buy no more old potatoes at all. It is not likely that she will buy new potatoes to the extent of 4 lbs. a day, as she did the old. They are still too expensive a form of food for that. She will perhaps buy 3 lbs. a day for 3d. (instead of 4 lbs. for 2d. as before), and this will involve some readjustment of expenditure on other articles of food, and perhaps in other branches of expenditure as well. But without following out these complex reactions we may at once grasp the fact to which we must now apply our closest attention, that the place which a pound of new potatoes takes on the marketer’s scale of preferences is not fixed. For if at 2d. she buys 2 lbs. but not 3 lbs., this shews that she prefers the second pound per week to 2d., but prefers 2d. to the third pound per week; and therefore a third pound stands lower than a second on her scale of preferences. If at 1½d. she buys 4 lbs. but not 5 lbs., it shews that she prefers the fourth pound to 1½d., but prefers 1½d. to the fifth pound—that is to say, that the fourth pound stands above and the fifth pound stands below 1½d. on her scale of preferences. If at 1d. she buys, say, 21 lbs. but not 22 lbs., it shews that she prefers the twenty-first pound to 1d., but prefers 1d. to the twenty-second pound. There is, of course, nothing inconsistent, anomalous, or mysterious in this. Each successive pound takes a lower place on the scale of preferences than the one before it, because the want to which it ministers is less urgent. “Second helps are never as good as first,” said a child, with a deep sigh, when she had finished her second plate of jam-roll. The pudding may be the same, but the child is different; for to the second help comes a child who has already had a first help—that is to say, an organism which can no longer enter into the same reactions with jam-roll as before. In order to say what place on the relative scale a unit of any commodity occupies in comparison with a unit of any other, we must know the how-many-eth unit (per day, week, or year) of each commodity we are talking about; or, in other words, we must know how much of each commodity we are to suppose is already possessed when we talk of the place which an additional unit will take on a man’s relative scale. If I have no supply of water and have seven loaves of bread to last me for a week, a pint of water will certainly occupy a higher place on my relative scale than a loaf of bread, but if I can already command twenty gallons of water for the week and have only one loaf of bread, another loaf will stand higher on my relative scale than a pint of water.
Hence the extreme importance of what is known as the doctrine of margins. We shall constantly find ourselves considering marginal services, marginal consumption, marginal significance, marginal expenditure, marginal values, marginal increments, and so on. (Marginal considerations are considerations which concern a slight increase or diminution of the stock of anything which we possess or are considering; the marginal service rendered to us by any commodity is that service which we should have to forgo if the supply of the commodity in question were slightly contracted; our marginal desire for more of anything is measured by the significance of a slight increment added at the margin of our present store. And the importance of this service, or the urgency of this desire, depends, as we have seen, on the quantity we already possess. If we possess, or have just consumed, so much of a thing that our desire for more is languid, then additions at the margin have little value to us; but if we possess or have consumed so little that we are keenly desirous of more, then marginal additions have a high value to us. And when we say of anything that we “would not take any more at a gift,” it means that its marginal value to us has been reduced to zero. (Thus by increasing our supply of anything we reduce its marginal significance and lower the place of an extra unit on our scale of preferences; and suitable additions to our supply will bring it down to any value you please.) Thus, whatever the price of any commodity that the housewife finds in the market may be, so long as its marginal significance to her is higher than that price, she will buy; but the very act of putting herself in possession of an increased stock reduces its marginal significance, and the more she buys the lower it becomes. The amount that brings it into coincidence with the market price is the amount she will buy.)
In our example we have supposed that when she finds new potatoes at 2d. per lb., the first and the second pound for the week come higher on her relative scale than 2d., but the third lower. So she buys 2 lbs., but no more, and this brings the marginal value into coincidence with the price. A fortnight afterwards she finds new potatoes at 1½d. If she only bought 2 lbs. now, the marginal value of a pound, though less than 2d., would be more than 1½d., which is now the price she would have to pay for it; and she would therefore be refusing a good bargain in not buying more; and so too with a fourth pound; but a fifth pound would be worth less than 1½d., and she would make a bad bargain in buying it. By getting 4 lbs., then, she brings the lowered marginal significance of her supplies into coincidence with the present price. And when the potatoes come down to 1d., by increasing her purchases to 21 lbs. she again brings down the marginal significance of the commodity into coincidence with the still further lowered price. Of course, her mind does not travel continuously over all the pounds from the fifth to the twenty-first, realising their gradual decline in significance until the margin that coincides with the new price is reached. It is only in the neighbourhood of the critical point that she consciously considers the question, but nevertheless the principle is at work all along the line. Its action brings her without consideration down to the point at which she has to consider.
In hundreds and thousands of suburban homes the question is asked every day, “How much milk shall we take in to-day, ma’am?” or “How much bread?” and the housewife knows without consideration that if she ordered one loaf of bread and one pint of milk, the marginal significance of bread and milk would be higher than their price, and if she said six loaves and five quarts of milk, the marginal loaf and pint would not be worth their price. Such orders, therefore, never enter into her head. But she deliberates, perhaps, whether she will want three loaves of bread or four, or three loaves and a twist, or three white loaves and a half-loaf of brown, and whether she shall take three quarts of milk or a pint more or less. Thus, whatever the terms on which alternatives are offered to us may be, we detect in conscious action at the margin of consideration the principles which are unconsciously at work in the whole distribution of our resources. When potatoes were at 2d. the marketer perfectly realised that a first or second pound were each of them worth more than 2d. When the price was 1½d. (if all other conditions remained the same) the first and second pound would still be worth more than 2d. each, but the marketer is scarcely conscious of this fact, she is conscious only that a fourth pound is worth more to her than 1½d. and a fifth pound less. By the time they have come down to 1d. she has ceased to realise that a first and second pound are still each of them worth more than 2d., and a third and fourth still each of them worth more than 1½d., nor has she ever at any time reflected that all between the fifth and twenty-first are worth more than 1d. each, which is what she gives for them, though she is still conscious that a twenty-first is just worth or just more than worth 1d., and a twenty-second just not worth it.
But the facts which she has ceased to consider, or which she never considered at all, are facts none the less; and it follows rigidly from all these considerations that whenever a considerable amount of any commodity is purchased at a given price, and some, but not so much, of that same commodity would have been purchased had the price been higher, then the purchaser gets for, say, 1d. a pound something for which he would have been willing to pay 2d. a pound had there been no alternative except to go without it. If he had been confined to these two alternatives of paying 2d. a pound or going without he would have divided up the commodity into two portions, with respect to one of which he would have embraced the former alternative of giving 2d. a pound for it, and with regard to the other the latter alternative of going without it. As things are, he gets the whole of the commodity at such a price that the least significant or marginal increment (the portion which he would go without if the price rose a little) is worth the price; and consequently all the other increments are worth more. What he gets, therefore, taken in bulk, is worth more than he pays for it.
Note, however, that it is more accurate to speak of the marginal significance of “the service rendered by the commodity” than of that of “the commodity” itself, because when the housewife, after consideration, has determined to get a fourth pound of new potatoes, thinking that it will be just worth 1½d. (the third having been worth more than 1½d.), that fourth pound is not earmarked as worth less than the rest, but is indistinguishable from the other three. But it remains true that 2 lbs. would have accomplished certain purposes or rendered certain services, and that 3 lbs. will render those services and certain additional services also, which additional services are still worth more than 1½d.; and further, that 4 lbs. will render the whole of the services rendered by 3 lbs., and certain additional services as well, and this last set of additional services are just worth 1½d. While we cannot individualise and earmark the fourth pound, therefore, or say that it performs a less valued service than the third, we can distinguish between the services rendered by 3 lbs. and the extra services rendered by 4. These extra services are what we call the marginal services of a pound; and these marginal services will vary as 4, 10, or 50 lbs. is the margin at which we take them.
To familiarise the reader with the idea of declining marginal significance as successive increments to a commodity accrue, and of the surplus value which we obtain over and above the price we pay in the case of all commodities of which we purchase considerable quantities, it will be well to take a somewhat elaborate and artificial example and to work it out in detail. We will suppose that a housekeeper, for her ordinary household, buys 7 lbs. of tea a month at 2s. The fact that she buys 7 lbs. shews that the difference between the service rendered by 6 lbs. a month and that rendered by 7 lbs. is estimated by her as worth at least 2s., otherwise she would not buy a seventh pound. And the fact that she buys no more than 7 lbs. shews than an eighth pound would be worth less than 2s. to her. But if we ask her to direct her mind to the higher values of an initial supply of which she does not usually think, and to tell us what the difference between having no tea at all and having 1 lb. of tea a month would represent to her, we may imagine that, on careful reflection, she might tell us (the figures are of course purely hypothetical, and in that sense arbitrary) that it would be 23s. The difference between 1 lb. and 2 lbs. a month she might estimate at 17s.; the extra satisfactions conferred by a third pound at 12s., and so on to 8s. for a fourth, 5s. for a fifth, and 3s. for a sixth pound. But if the difference between no tea and a pound of tea a month is worth 23s., and the difference between 1 lb. and 2 lbs. is worth 17s., the total difference between no tea and 2 lbs. a month is 23s. + 17s. or 40s; so that if the alternative were offered the housekeeper of having no tea or a 2-lb. packet per month, she would pay 40s. for the 2 lbs. sooner than go without it. Again, we have seen that she estimates the difference between 2 lbs. and 3 lbs. at 12s. If her option therefore were to have no tea, or a packet of 3 lbs. per month, sooner than go without she would pay 52s. for the 3 lbs. Proceeding in the same way we see that the difference to her between having no tea at all and 4 lbs. a month is represented by 60s., and the difference between no tea and 6 lbs. a month by 68s., and since we know that the last pound is worth at least 2s. to her the difference between no tea and 7 lbs. a month appears to be at least 70s. a month. Now, as a matter of fact, the tea being 2s. a pound, she gets her 7 lbs. of tea for 14s. a month. Thus she gets for 14s. that for which she would have paid at least 70s. sooner than go without it.
*3
This result, though it may seem rather startling, is in reality no more than the analytical restatement of the sufficiently obvious and familiar fact that a well-to-do person who has considerable supplies of most of the articles of his current consumption could support a small deduction without feeling it much, whereas if his supplies were reduced by three-quarters all round he would very distinctly feel any further small deductions from the residue. At his present margin small economies and adjustments do not cut into the quick, whereas at a margin further back they would; yet he pays no more for that proportion of his supplies that keeps him from starvation or from the feebleness of inanition than he does for that proportion which ministers to his comfort or perhaps his superfluity.
These considerations will throw much light on the distinction which the older economists drew between “value in use” and “value in exchange,” a distinction which we should express under the terms “total significance” and “marginal significance.” The total significance (value in use) of any commodity which we consume may be represented by the sum of money which we should require as an equivalent for entirely surrendering it, while the marginal significance (value in exchange) of a unit is represented by the sum of money for which we would consent to have our supply curtailed by one unit; and we have seen that if our supply consists, for example, of 10 units, its total significance (value in use of the whole) will be greater, and may be enormously greater, than ten times the significance of the marginal unit (value in exchange, or market value, of the whole). The example of the tea will make it very clear that as the “value in use” of our supply, taken as a whole, increases, its “value in exchange” per unit (coinciding with its marginal value) declines. The value in use reaches its maximum when we have as much as we want and the marginal value has become zero.
Now since it is the marginal values that we are always considering, our minds are always engaged in appraising the least valued part of the commodity or service in question. One of the favourite examples of the distinction between “value in use” and “value in exchange” in the older books was the air we breathe, which obviously has an extremely high value in use, though under ordinary circumstances it has no value in exchange; the reason being that, since we all have as much of it as we want, its marginal significance has sunk to zero, though its total significance remains greater than can be measured in money. And accordingly, whenever the supply is for any reason curtailed, and can be increased or diminished by suitable appliances, air acquires a marginal significance, and may have an exchange value. If a mine-owner wished to improve his system of ventilation and asked for tenders or estimates, the engineer might put different systems before him, the more expensive ones providing for a larger volume of air to pass through the workings per minute, and the cheaper ones for less. In weighing them the owner would estimate, in each case, the additional advantages of the increased supply of air, and would consider whether they were worth the increased cost. He would therefore be considering with some precision the marginal value of air at several alternative margins. But no owner of deep mines would ever consider whether the mines ought to be ventilated at all or not. That is to say, he would never consider the most important part of the question, but would take it for granted. It would not be the total but the marginal value of the supply of air in the workings that would engage his thoughts.
Again, it is impossible to make any pecuniary estimate of the total value, or value in use, of our food collectively, but we are constantly considering its marginal value. We have already
*4 spoken of young men and women living on narrow means, who never consider whether they shall go without food altogether, and not often whether they shall go without a meal, but in whose minds an almost daily debate arises as to whether to spend an extra penny on a piece of cheese, or whatever it may be, at their midday meal. They are perpetually considering the marginal 1d. or ½d. per diem spent on food, though they seldom consider the remoter units which are higher up on the scale and are secured without deliberation.
It is obvious, then, that whereas the successive units of our supply of any commodity occupy different positions on our scale of preferences, it is only the units close to the margin of actual or contemplated possession that engage our close attention. Thus the scale of equivalence to which we give particular consideration is that of the marginal units of our supplies. Henceforth, therefore, whenever we speak without special qualification of the place which a unit of any commodity occupies on our scale of preferences we must always be taken to mean the marginal unit; and we must remember that as the marginal significance of anything declines owing to the supply increasing, the volume of the total satisfaction derived from it grows.
*5
We must now proceed to a closer examination of the nature of marginal units, marginal increments, and marginal significances. And in particular it will be necessary to justify the practice of speaking of the marginal significance of a commodity, at such and such a point, as measured indifferently by the value of a small increment or the value of a small decrement. This practice is constantly and rightly followed in books on Economics, but since our whole theory rests on the fact that each successive increment renders less important services than the last, and that each successive decrement involves more serious privations than the last, it seems unwarrantable to assign an exactly equivalent value to the two successive increments that come one just before and the other just after a given point. The explanation and justification of this apparently illegitimate practice must now be given; and the reader will find it convenient to read it with the table that faces page 47 open before him. The beginner may perhaps find the investigation on which we are now entering (and which extends to page 71) of an unusually severe character. It is of the nature of grammar, and a complete mastery of it is necessary for an accurate and scholarly pursuit of the study; but as it is sometimes best when studying a new language to try, at a very early stage, to read it as best one can, and then to take up the grammatical details at the points at which the want of them is felt, so if the reader loses interest in the following argument or loses hold of it, he may find some help in reading further on, beyond page 71, to see what it is all leading up to and how it is underpropping and defining the ideas which we must assume in all our future investigations.
It is obvious that the reasons which make a second pound of tea of less value than a first, and a third of less value than a second, will also make the first half-pound more valuable than the second half-pound, and so forth. The consumption of any pound or other specified quantity of tea will naturally begin at a higher rate of significance than it ends at, and the decline will be continuous. The process by which we combined the more valued first pound (23s.) and the less valued second pound (17s.) into a total of two pounds at a value of 40s. may be reversed, and the total of 17s. for the second pound may be resolved into the significance of a more valued first half and a less valued second half pound. If the purchaser were at liberty to buy in half-pounds, therefore, he would be willing to pay more than half 17s. for the first half of the second pound, sooner than go without it, but if he had this he would value the second half-pound at less than half the 17s.; and so throughout.
Further, we have supposed that while each additional pound has a lower significance (measured by the successive declines from 23s. to 17s., from 17s. to 12s., from 12s. to 8s., and so on), each successive decline in value is less marked than the one before it (the declines being by steps of 6s., 5s., 4s., etc., respectively); so if we were to go by half a pound at a time we should expect in like manner a regular decline in the significance of each half-pound, following a similar law. If, then, we ask our housekeeper for estimates of the significance not of successive pounds but of successive half-pounds, we shall expect her to give us a new series of hypothetical prices, consistent with the previous data as to the significance of successive pounds. Thus, if we ask her to start on the supposition that she has 2 lbs. of tea per month, and to go into closer details than the estimate of 12s. for the third pound and 8s. for the fourth which she has already given us, we may imagine her estimating the significance of the four half-pounds, taken severally. If she were to say, 6s. 6d. for the fifth half-pound, 5s. 6d. for the sixth, 4s. 6d. for the seventh, and 3s. 6d. for the eighth, this would give results fairly consistent with her original statement. Each successive half-pound would in this case decrease in significance, as compared with the one before it, at a uniform rate of one shilling. But we have already noticed that this is not the exact law followed by the original estimates. The decline from 23s. to 17s., and from 17s. to 12s., etc., is not uniform. It follows a law of decreasing rapidity. The difference may be made clear by tables. The original estimate may be set out thus:—
| Values of Successive Lbs., Declining. |
Steps by which Values Decline, themselves Declining. |
Rate at which Decline Decreases, Uniform. |
|
| 1st | 23s. | ||
| 6s. | |||
| 2nd | 17s | 1s. | |
| 5s. | |||
| 3rd | 12s. | 1s. | |
| 4s. | |||
| 4th | 8s. | 1s. | |
| 3s. | |||
| 5th | 5s. | 1s. | |
| 2s. | |||
| 6th | 3s. |
Whereas if the four successive half-pounds are estimated as we have supposed, we should have—
| Values, Declining. |
Steps of Decline, Uniform. |
| 6s. 6d. | |
| 1s. | |
| 5s. 6d. | |
| 1s. | |
| 4s. 6d. | |
| 1s. | |
| 3s. 6d. |
If, however, the estimates had not been 6s. 6d. but 6s. 6¾d. for the fifth half-pound, not 5s. 6d. but 5s. 5¼d. for the sixth, 4s. 5¼d. for the seventh, and 3s. 6¾d. for the eighth, we should have had—
| Values, Declining. |
Steps by which Values Decline, themselves Declining. |
Rate at which Decline Decreases, Uniform |
| 6s. 6¾d. | ||
| 1s. 1½d. | ||
| 5s. 5¼d. | 1½d. | |
| 1s. | ||
| 4s. 5¼d. | 1½d. | |
| 10½d. | ||
| 3s. 6¾d. |
in perfect consistency with the law manifested by the original estimates for successive pounds.
At this point the reader may feel that an outrage is being offered to his common sense in asking him to suppose that estimates of such accuracy can be given. This is perfectly true; but the outrage that has now been discovered and resented was committed when the original estimates of 23s., 17s., etc., were offered for acceptance. For, concealed under the round numbers there lay a law which implied, or at least suggested, that they were accurate not only to the nearest farthing, but absolutely. This is a manifest impossibility; but if we carefully examine how and why it is impossible, we shall get a good deal of incidental enlightenment, and shall then be able to pursue our investigations on this impossible hypothesis without peril.
Why, then, is this accuracy unthinkable? To begin with, any such estimates as we supposed ourselves to obtain originally would not really be based entirely on a true sense of the significance of the several increments, but would be partly determined by sums of money on which the mind easily rests, and with which it is accustomed to deal. One can imagine, for instance, a housekeeper saying, under certain circumstances, that she would give 8s. for a pound of tea but “not a penny more,” and even actually refusing to give 8s. 1d.; but it is not easy to imagine her fixing on 7s. 9½d. as the exact sum past which she would not go, and refusing to pay 7s. 10½d. And again, whether she fixed on 8s. or 7s. 9½d., our housekeeper’s declaration, that she would not give a penny or that she would not give a farthing more, would probably be nothing but a desperate determination to take her stand somewhere. She knows, let us say, that 7s. would be a good bargain and that 9s. would be more than the thing is worth. But she also knows that you can go from 7s. to 9s. by steps of a farthing each, and that unless she makes a stand she may be drawn on, always thinking that a single farthing is not worth fighting about, till she becomes conscious that she has gone too far; like the man who complained that he never knew when he had had enough to drink, though he knew when he had not had enough and when he had had too much. So, without pretending that she can really hit the exact value to a farthing, she (more prudent than the toper) pulls up somewhere and refuses to be worried any more. So she says, “I’ll give you 7s. 9½d. Take it or leave it.”
Therefore, when she mentions an outside price, she may, in the first place, be influenced by associations or habits, so that the price named is not based entirely on a deliberate estimate of the significance of the tea; and, in the next place, she is not in any case giving a perfectly precise and immovable estimate, for she cannot draw a definite line. There are prices which she is quite sure the thing would be worth, and prices which she is quite sure it would not be worth, but the transition from one to the other is gradual. The two are separated by a band rather than by a line, and even this band shades off, so that you cannot exactly determine its limits. There is an indefinite penumbra, as well as an umbra.
Thus, if we said that the original estimates were reliable to a shilling, we should mean that the housewife would certainly, without hesitation, give 22s. for the first pound, and that she would not entertain the idea of giving 24s. for it; and that would mean,
a fortiori, that she would not give 23s. for 15 oz. of tea, for the difference between 15 and 16 oz. is greater than that between 23s. and 24s. To suppose such an approach to accuracy is not manifestly absurd. But to say that the estimate is accurate to a farthing would be to say that the housewife would give 23s. for a pound of tea, but not for a quantity that fell short of a pound by one sixty-ninth of an ounce. This does strike us as manifestly absurd. But we can give no definite answer to the question, “At what point between a shilling and a farthing does the hypothesis of accuracy become ridiculous?” Clearly one person might realise an indefinitely closer approximation than another, and we may therefore theoretically assume any degree of accuracy that we like. Even if we boldly make the absurd assumption of accuracy to a farthing, or to indefinitely smaller fractions of a penny yet, we shall merely be endowing our purchaser, for theoretical purposes, with normal powers raised to an abnormal degree of keenness. If we do this with our eyes open, the extreme supposition of estimates accurate down to an indefinitely minute fraction of a farthing or of an ounce, while illustrating the principles we are investigating in their inmost recesses, will not in any way mislead us.
Let us assume, then, that our data are reliable within any given degree of accuracy that we may find necessary to demand as we proceed, and that the law which they reveal applies consistently and uniformly, throughout the region which we are to submit to special investigation.
*6
We may now proceed to set forth the details of the table facing page 47, which may be carried out as far as we like. We have already broken up 12s., the significance of the third pound, into 6s. 6¾d., the significance of its first, and 5s. 5¼d., the significance of its second half; and have dealt with 8s., the significance of the fourth pound, in the same way. Carrying the process still further we shall find that 5s. 5¼d., the significance of the last half-pound that completes 3 lbs., may be taken as made up of 2s. 10d. plus 7/8 farthing for its first quarter, and 2s. 7d. plus 1/8 farthing for its second, and in like manner the 4s. 5¼d. of the next half-pound as made up of 2s. 4d. plus 1/8 farthing for the first quarter and 2s. 1d. plus 7/8 farthing for the second. The reader can test the consistency of these figures and those that follow by taking out the successive differences and satisfying himself that they follow the law of regular and equal decline that we have supposed to characterise the whole series, as implied in the original estimates. The top and bottom rows of this table (neglecting for the present the central row) set forth the estimated values of the four successive half-pounds, quarter-pounds, and smaller fractions of a pound down to the four successive quarter-ounces, that lie two and two on each side of 3 lbs.; and the reader may satisfy himself by examination that the law of the series is complied with in every case. Thus the four half-ounce increments two and two on each side of 3 lbs. run—
| Values. | Difference. | Decline in Differences. |
| 3d. 3 135/4096 f. | ||
| 774/4096 f. | ||
| 3d. 2 3457/4096 f. | 6/4096 f. | |
| 768/4096 f. | ||
| 3d. 2 2689/4096 f. | 6/4096 f. | |
| 762/4096 f. | ||
| 3d. 2 1927/4096 f. |
We are assuming an impossible degree of accuracy and precision throughout, but we must now distinguish between the different sets of distinctions we are drawing. Even when we are dealing with quarter-ounces, it requires no stretch of imagination to suppose that the quantities themselves are appreciable. A quarter-ounce of tea is not a negligible thing. With the aid of an infusor it can be made to give two cups of tea. Even with tea at 2s. a pound, a careful housekeeper considers it more or less carefully when filling her teapot, and adds or withholds it by a conscious estimate. On the supposition of its being added in the neighbourhood of the third pound it would be worth more than 1¾d. to our housekeeper. So far, then, we are dealing with easily appreciable magnitudes. But when we come to consider not the values themselves but the differences between them as the quarter-ounces succeed each other we are on very different ground. The table of approximations facing page 63 may help the reader to appreciate this. If our estimates are reliable to the nearest eighth of a penny, but not to finer fractions, it will be seen that there will be no appreciable difference in value between each of the four quarter-ounces, two and two, before and after the third pound. And even in the half-ounce increments there will be no appreciable difference in value between the last two increments before, or between the first two after, the third pound. What is the meaning, then, of the register of an appreciable difference between the second and the third half-ounce? The complete table and the general law of the series shew the difference between the second and third half-ounces to be less than that between the first and the second, and yet the table of approximations sets forth the smaller difference as appreciable and the greater as inappreciable. What is the sense of that?
To answer this question we must touch on a principle of which there are many familiar illustrations: the principle, namely, that very small differences do not consciously affect us severally, but exercise a cumulative effect which emerges into consciousness at a certain point. It is probably a common experience for a man looking at the seconds hand of his watch to think at first that the watch has stopped. It requires several seconds, during which he is conscious of the passing of time but not conscious of the moving of the hand, before the cumulative effect of the successive small movements makes itself felt. Thus the sense of declining value might be subconscious for two small units, and then might make its cumulative effect felt all at once in the transition to the third. To a mind capable of no finer discriminations than eighths of a penny, the difference between the values of the successive half or quarter ounces would be too small to make itself felt at every step. It would only be if we took units as large as an ounce that each of them would be sure to contain at least one such critical point at which the effect would become conscious.
We have now distinguished between sensitiveness to the importance of an addition or subtraction of a quarter-ounce of tea, and sensitiveness to the
difference of importance between successive additions or subtractions, and have seen that it needs a much finer sense to be regularly and continuously conscious of the latter than of the former. The difference between the significance of the two quarter-ounces that lie on either side of the 3-lb. line is less than a one-hundred-and-fifty-sixth of the significance of either of them. But it will be remembered that the law revealed in our original data implies that there is not only a decline in the significance of successive units, but that the decline itself is not uniform. In order that this characteristic should reveal itself as a regular phenomenon to a mind only capable of consciously appreciating eighths of a penny, we should need to give still larger room for cumulative effects; and a consultation of the table of approximations will shew that the action of this law is not traceable in any units smaller than a quarter of a pound. The quarter-pounds give—
| 2s. 10¼d. | ||
| 3¼d. | ||
| 2s. 7d. | ¼d. | |
| 3d. | ||
| 2s. 4d. | ¼d. | |
| 2¾d. | ||
| 2s. 1¼d. |
but the 2-oz. increments give—
| 1s. 3 7/8d. | |
| 6/8d. | |
| 1s. 3 1/8d. | |
| 6/8d. | |
| 1s. 2 3/8d. | |
| 6/8d. | |
| 1s. 1 5/8d. |
If the reader will now turn back to page 47 and recall the problem that led us into the present investigation, he will perceive that the impossibilities involved in our supposition of minute accuracy strengthen our case instead of weakening it. We noted that whereas our general theory requires us to believe that for any given margin the last unit before will have a higher significance than the next unit after, it is nevertheless customary to ignore the difference in value and to speak of the units on each side of the given point as having precisely the same significance. And we now see that for any degree of accuracy and sensitiveness, however impossibly fine, with which we choose to endow our observer, this proceeding is absolutely justified if the units in question are taken small enough. We can always take increments so large that the
significance of the addition or subtraction of each one of them can be distinctly felt and estimated, but at the same time so small that the
difference between the significance of two of them taken in succession cannot be separately estimated, and therefore not only may be, but must be, ignored.
To sum up. There are limits to the fineness of discrimination of which any mind is capable. Even the trained astronomer is not supposed to be able to distinguish the passage of time more accurately than to tenths of a second. But in his case the thing to be measured flows uniformly and continuously; whereas in the case of the tea our objective measurements cannot be supposed to present any such uniformity and continuity. The quality of different spoonfuls of tea is not uniform, still less is that of individual leaves. The vibrations of the nerves may themselves be supposed to respond, not continuously but cumulatively, to minute changes of external stimulus; and the surrounding conditions change not only from month to month but from second to second, so that even the most closely registering mind would not have a series of uniform and continuous phenomena to register.
We cannot, then, make our estimates indefinitely fine, and to whatever degree of fineness they actually attain, we shall be able to take increments, each of which has a definite significance, and two of which taken in succession may be treated as having the same significance.
This completes our justification of the practice of treating the marginal decrement and the marginal increment as identical in value, on the supposition that they are sufficiently small; and the reader who feels that he has reached the limit of his present capacity for following this kind of investigation may provisionally pass on to page 71. But the most perfect and satisfying part of the theory still remains to be expounded, and the reader’s grasp of the subject will not be finally confirmed until he has mastered it.
The conception of “rate” on which the exposition we are now to enter upon depends is very familiar in its elementary applications. 3s. 9d. a yard is the same rate as 1¼d. an inch, 3s. a yard the same as 1d. an inch, and 2s. 3d. a yard as ¾d. an inch.
| 3s. 9d. | a yard is | 1¼d. | an inch. |
| 3s. | “ | 1d. | “ |
| 2s. 9d. | “ | ¾d. | “ |
So if I give 3s. for a yard I shall be paying a higher sum, but a lower rate, than if I pay 1¼d. for an inch, but both a higher sum and a higher rate than if I pay ¾d. for an inch. And if I take the difference between a yard at 3s. 9d. and a yard at 3s. I shall be dealing with a larger sum than if I take the difference between an inch at 1¼d. and an inch at ¾d., but the sum, though larger in itself, will be smaller in proportion to the quantities compared, or, in other words, will represent a smaller difference in rate. Now let us look carefully at the three lines of entries in the central row of
Table I.
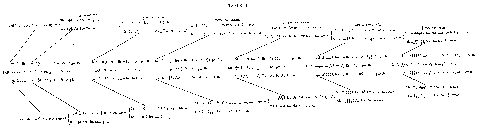
The last half of the third pound is worth 5s. 5¼d., which is both a lower sum and a lower rate than 12s. a pound; whereas 4s. 5¼d. for the first half of the fourth pound is a lower sum but a higher rate than 8s. a pound, for it is a rate of 8s. 10½d. per pound. Thus in comparing 12s. with 8s. we shall expect to find not only a greater difference, but a greater difference of rate, than between 5s. 5¼d. and 4s. 5¼d. And so we do; for the difference of rate in the one case is 4s. (half the lower and a third of the higher rate), and the difference in the other case is only 2s. (less than a fifth of the higher and less than a fourth of the lower rate). The difference between the half-pounds, then, is not only less than that between the pounds, but less than half of it, because it is a difference between half-pounds more like each other than the pounds were. In like manner, if we had taken the first half of the third pound and the second half of the fourth, we should have had the rates—
| 1st ½ lb. | 6s. 6¾d. | per ½ lb. | = 13s. 1½d. | per lb. |
| Difference | 3s. | “ | = 6s. | “ |
| 4th ½ lb. | 3s. 6¾d. | “ | = 7s. 1½d. | “ |
where the difference between the half-pounds (3s.) would have been less indeed than the difference between the pounds (4s.), but more than half of it, because it would have been a difference between half-pounds less like each other than the pounds.
So the total difference of 4s. in value between the third and the fourth pounds may, if we like, be analysed into a difference of 3s. between the extreme half-pounds and a difference of 1s. between the mean half-pounds; and returning now to the difference between the inner or mean half-pounds that lie on each side of the 3-lb. point we may again analyse each of them into the extreme or most unlike and the mean or most like quarters. Taking the inner quarters we shall find them to be worth 2s. 7d. + one-eighth of a farthing, and 2s. 4d. + one-eighth of a farthing, respectively; the difference being 3d., or less than one-tenth of the higher and less than one-ninth of the lower amount. And the difference between the rates (10s. 4 1/8d. and 9s. 4 1/8d.) is only 1s. The table continues the successive halvings of the quantities considered till they are only a quarter of an ounce each, and at every step it rejects the more unlike outside halves and retains the more like inside halves of the pair last considered, thus narrowing down the increments, so that the difference between them not only goes on growing smaller, because the values themselves are smaller, but also becomes a smaller and smaller proportion of those smaller values themselves, because the latter are being made more and more like each other by the successive rejections of the most unlike portions of each pair. We see that the difference between the successive two-ounce increments, valued respectively at 1s. 3d. 0 33/64 f. and 1s. 2d. 1 33/64 f. is only ¾d., which is less than 1/19 of the lower and less than 1/20 of the higher term of comparison; and at the end of the table we find the difference between the two successive quarter-ounces on either side of the 3-lb. margin to be only 3/64 f., of which is less than 1/156 of the lower and less than 1/157 of the higher. As we compare smaller and smaller increments on each side of the 3-lb. margin we see that the significance of the higher one falls both absolutely as a quantity and relatively as a rate, because it is taken closer and closer up to the less significant end of the third pound,
*7 whereas the significance of the lower one falls absolutely as a quantity, but rises relatively as a rate, because it is taken closer and closer up to the more significant end of the fourth pound. Thus the upper and lower rate are constantly approximating to each other, and the difference between them is constantly becoming a smaller and smaller fraction of either. The falling series (read for convenience to the nearest 1/8d. on the top line of the central row of
Table II)
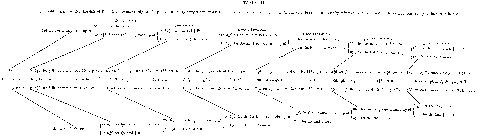
runs, as we pass from the pound to the half and quarter pound, etc.—
| 12s. | 10s. 10½d. | 10s. 4 1/8d. | 10s. 1d. | 9s. 11½d. | 9s. 10¾d. | 9s. 10 3/8d. |
whereas the corresponding rising series (read on the lowest line) is—
| 8s. | 8s. 10½d. | 9s. 4 1/8d. | 9s. 7d. | 9s. 8½d. | 9s. 9¼d. | 9s. 9 5/8d. |
The difference between each successive pair (read on the central line of either Table I. or Table II.) declines in accordance with a regular law, each difference being one half of the last. Thus by continuing the process we could make the difference as small as we pleased, though we could never make it nothing; and so we can bring the upper and the lower rate as near to each other as we please, though we can never make them identical. All this, together with the suggestion of the next step in our advance, will be made clearer by the inspection of the accompanying
diagram.
 The reader will probably have no difficulty in perceiving, as a general truth, that if two quantities approach each other indefinitely and can be brought as nearly as we please to identity but cannot be made identical, and if the one is always falling and the other always rising, they must both be falling and rising towards a certain fixed point that always lies between them. Thus the falling series, 3, 2½, 2¼, 2 1/8, and the rising series, 1, 1½, 1¾, 1 7/8, are falling and rising respectively towards 2. No member of either series will ever reach, it, but the successive members approach it more and more nearly, and can be made to approach it as nearly as we please. If we fixed upon any quantity other than 2, ever so little larger or smaller, it would follow that either the descending quantity or the ascending quantity could pass it, by getting nearer than it to 2; for either can be made to get as near to 2 as we like, and we might like to get it nearer than this other quantity.
The reader will probably have no difficulty in perceiving, as a general truth, that if two quantities approach each other indefinitely and can be brought as nearly as we please to identity but cannot be made identical, and if the one is always falling and the other always rising, they must both be falling and rising towards a certain fixed point that always lies between them. Thus the falling series, 3, 2½, 2¼, 2 1/8, and the rising series, 1, 1½, 1¾, 1 7/8, are falling and rising respectively towards 2. No member of either series will ever reach, it, but the successive members approach it more and more nearly, and can be made to approach it as nearly as we please. If we fixed upon any quantity other than 2, ever so little larger or smaller, it would follow that either the descending quantity or the ascending quantity could pass it, by getting nearer than it to 2; for either can be made to get as near to 2 as we like, and we might like to get it nearer than this other quantity.
The law by which, and the rate at which, the descending and the ascending series respectively approach this common point need not be identical. Thus the descending series, 7, 7 × 2/3, 7 × 4/7, 7 × 8/15, and the ascending series, 3, 3¼, 3 3/8, 3 7/16, will both be found to be approaching by different laws the limit of 3½. If they are taken two and two, 7 and 3, 7 × 2/3 and 3¼, etc., the quantity 3½ will be found always to lie between the two members of each pair. Both members may be made to approach this quantity as nearly as we please, and neither can ever be made to reach it by continuing the processes by which the series are formed.
The reader will now have no difficulty in perceiving that between the steadily descending series of rates, 12s., 10s. 10½d., …, and the steadily ascending series of rates, 8s., 8s. 10½d., …, which can be made to approach each other as nearly as we please, but can never be made identical, there must lie some rate that never changes and is the limit of both; but if he is not a mathematician he will have to take it on trust that that rate is 9s. 10d.
We saw on page 56 that whatever we suppose to be the smallest quantity that the mind can register we can always fix upon two successive increments so large that the mind can appreciate the significance of each of them, but so small that it cannot appreciate the difference of significance between the two. But now let us suppose that there is a series of phenomena, obeying the law we are examining, so regular that there is no unit, however small, which would make it discontinuous—that is to say, which would reduce it to jumps. The passage of time may be taken as such a continuous phenomenon. And let us further suppose that there is a mind of such quality that no fraction, however minute, is small enough to escape being registered by it. This is what would be meant by supposing that our law worked with absolute accuracy. Let us make this supposition therefore. It would follow that our Table I. could be carried out as far as we chose, and the point would never be realised at which the differences between the successive units or the law of the decline in the successive differences would become too small to note. What should we then have? We should have a series of descending values beginning with 12s. and going down the series 10s. 10½d., etc., always approaching nearer to 9s. 10d. as we halved the unit; and a series of ascending values 8s., 8s. 10½d., etc., also always approaching nearer to 9s. 10d. as we halved the unit, but never reaching it. And if we took a sum ever so little higher than 9s. 10d. the falling series would at last get below it, or if we took a sum ever so little lower than 9s. 10d. the rising series would at least get above it. The sum of 9s. 10d., then, is absolutely fixed, and it represents a rate which is the limit alike of the significance of the third pound as you come down to its less significant end, and of the fourth pound as you come up to its more significant end. You may think of it equally well as the end of the third pound or as the beginning of the fourth. If, then, I say that 9s. 10d. a pound is the theoretical marginal value of tea, at the margin of three pounds, I mean that it is theoretically never quite true that either the last increment before or the next increment after the three-pound margin is valued at the rate of 9s. 10d., but that the rate of 9s. 10d. always lies theoretically between the values of these two increments, and the smaller they are the smaller, proportionally, is the theoretical error involved in saying that either or both of them is identical with it.
We may now epitomise our results. When we speak of the value of the marginal unit (at any given margin) we shall often mean the amount at which the last pound, or whatever it may be, is valued as a whole by the possessor, and shall not mean to imply that the next pound would be valued at the same amount. Sometimes we shall be thinking of the next pound to be obtained and shall call that the marginal pound without meaning to imply that the last pound possessed is not valued at a perceptibly greater amount. Which of these two pounds (each of which touches the actual margin with its lower or its upper limit) we mean, will depend upon the matter in hand at the moment, and the context will prevent any ambiguity. But sometimes the term “marginal value of a unit” is to be understood as applying at the same time both to the last and to the next unit; and in this case the implication will be that the units are large enough to be distinctly felt and valued, but so small that the difference of value between the two successive units is not felt. And this will always be a legitimate supposition. And lastly, we shall sometimes speak not of the marginal value of a unit of the commodity, but of the marginal value of the commodity per unit. And that expression would apply either to the actual rate of significance per unit of the increments just described, or to the theoretically limiting rate, the nature of which we have been examining. The implication in this last case would be that even though, however small the units we take, the last before the margin should always be valued at a little more and the next one after the margin at a little less than this rate, yet either can be brought as near to it as we please, and that it will always lie between them. It represents the point at the margin itself which the upper unit always touches at its lower end, stretching up from it, and the lower unit touches at its upper end, stretching down from it.
If we had taken any other margin, such as 5 lbs. or any other original set of estimates, we should have reached different, but always analogous results, and should have arrived at the same conclusions as to the legitimacy of speaking of marginal values, and as to the exact meaning of assigning such and such a marginal value to any commodity at any given margin. On our original data the marginal value of tea to this particular purchaser would be 19s. 10d. at the margin of 1 lb., 14s. 4d. at 2 lbs., 9s. 10d. at 3 lbs., 6s. 4d. at 4 lbs., 3s. 10d. at 5 lbs., and 2s. 4d. at 6 lbs. Marginal values intermediate to these will, of course, be reached at intermediate points. The marginal value of 17s. approximately corresponds to 1.49 lbs.; that of 7s. 6d. to 3.63 lbs.; that of 5s. to 4.48 lbs. The reader is supposed, if not a mathematician, to take it on trust that these special values are implicit in the original data, but he is supposed to understand, as the result of our investigations, that the original data, or any other similar group, necessarily imply the theoretical existence of definite marginal values, continuously declining, though they do not necessarily give us the means of determining them.
*8 The estimates may be varied in any way we please, but so long as we suppose, in every case, a declining (though not necessarily a regularly declining) significance in value as successive increments are secured, we shall always be able to attach a precise significance to the conception of marginal value and shall always find it declining as the stream of supply broadens.
In some of our future examples we shall directly compare the marginal significances of two different commodities with each other without using money as a medium of comparison. The transition to this method may be made clearer and safer by certain considerations for which we are now sufficiently prepared. Let us suppose that there is some commodity other than tea, for a first unit of which our tea-consumer would be willing to give 17s. 9d., for a second unit 12s. 3d., for a third 7s. 9d., and for a fourth 4s. 3d., for a fifth unit 1s. 9d., for a sixth 3d. The table presents these estimates:—
| 1st. | 2nd. | 3rd. | 4th. | 5th. | 6th. |
| 17s. 9d. | 12s. 3d. | 7s. 9d. | 4s. 3d. | 1s. 9d. | 3d. |
This series, as the accompanying table shews, follows a law similar to that we have assumed as regulating the significance of tea.
*9
| Values of Successive Units, Declining. |
Steps by which Values Decline, themselves Declining. |
Rate at which Decline Decreases, Uniform. |
| 17s. 9d. | ||
| 5s. 6d. | ||
| 12s. 3d. | 1s. | |
| 4s. 6d. | ||
| 7s. 9d. | 1s. | |
| 3s. 6d. | ||
| 4s. 3d. | 1s. | |
| 2s. 6d. | ||
| 1s. 9d. | 1s. | |
| 1s. 6d. | ||
| 3d. |
But it does not begin so high, and it threatens rapidly to reach zero—that is to say, the point at which another unit would not be taken at a gift. One might suppose, for instance, that it was important to a man to be at a neighbouring place, some fourteen miles distant, once a month, so that he would post there if necessary. A second and a third visit per month might have considerable but declining significance to him. A fourth visit might be just worth making if he had to pay first-class railway fare, a fifth not worth third-class fare, a sixth a matter of practical indifference, and a seventh perhaps a nuisance. In such a case half or quarter units might be interpreted as bimonthly visits, etc. Or an approximation to the hypothetical figures might be furnished by a suitably selected unit of some kind of fruit which has been medically prescribed to one member of a family, and is much desired for (or by) other important or importunate members of it, but any great abundance of which is regarded as a danger to the health of the nursery or the morals of the kitchen. It will be best, however, not to dwell on any imaginative realisations, which might easily become more of a burden than a support, and to speak not of tea and journeys to Crankstead, or of tea and apples, but simply of commodity A and commodity B.
Now the same methods which we applied (asking the reader to take them on trust) to ascertaining marginal values of tea, which has now become our commodity A, if applied to the data of commodity B would yield the following marginal values at the end of each unit:—14s. 10d. at a margin of 1, 9s. 10d. at a margin of 2, 5s. 10d. at a margin of 3, 2s. 10d. at a margin of 4. It will be convenient here to tabulate the estimates of the successive units of A and B which were given us, and also of the marginal values they imply.
| Values of Units | ||||||
| 1st. | 2nd. | 3rd. | 4th. | 5th. | 6th. | |
| A | 23s. | 17s. | 12s. | 8s. | 5s. | 3s. |
| B | 17s. 9d. | 12s. 3d. | 7s. 9d. | 4s. 3d. | 1s. 9d. | 3d. |
| Marginal Significances | ||||
| At Margin of | ||||
| 1st Unit. | 2nd Unit. | 3rd. Unit. | 4th Unit. | |
| A | 19s. 10d. | 14s. 4d. | 9s. 10d. | 6s. 4d. |
| B | 14s. 10d. | 9s. 10d. | 5s. 10d. | 2s. 10d. |
It will be noted that if the individual who forms these estimates has a supply of 3 units of commodity A and 2 units of commodity B per month (or other unit of time), the marginal significance of each of them will be at the rate of 9s. 10d. per unit. This means, in rigid theory, that any addition to either of them, however small, is valued by him at something less than the rate of 9s. 10d.; and any subtraction, however small, would be felt at the rate of something more than 9s. 10d. So that he would be the loser by curtailing his consumption of either by ever so small a fraction of a unit, in exchange for increasing his supply of the other by the same fraction. But if we are not speaking of an absolute theoretical margin, but of actual estimates, we shall mean that small increments or decrements of either commodity would alike be estimated, in this region, at the rate of 9s. 10d. a unit, so that it would be a matter of indifference to the possessor whether his supplies remained as they are, or a very small fraction of a unit were taken away from his supply of one of the commodities, and a like amount added to his supply of the other. In either of these cases we should say that if the terms on which the choice between the two commodities is offered him are terms of par—that is to say, if he can get any unit or portion of a unit of either of them by sacrificing the same quantity of the other,—he will have no interest in making any change, and his supplies therefore are in a state of equilibrium. Hence we may sometimes say that if a man’s supplies are in equilibrium (at current prices) he would lose by making any change, and sometimes that a small change of one commodity for the other, on the terms open to him, would be a matter of indifference. It will depend upon whether we are considering quantities large enough to embrace a sensible rise or fall of significance within their several boundaries. Equilibrium does
not exist if the possessor knows that he would gain by exchanging, on the terms open to him, a portion, however small, of either of the commodities for the corresponding portion of the other.
Thus, if the man had five units of A and 2 of B we should have—
| Value of last Unit Possessed. |
Value of next Unit to be Acquired. |
|
| A | 5s. | 3s. |
| B | 12s. 3d. | 7s. 9d. |
And there will be an obvious advantage in giving a unit of A (5s.) for an extra unit of B (7s. 9d.). The man would then have 4 units of A and 3 of B, and we should have—
| Value of last Unit Possessed. |
Value of next Unit to be Acquired. |
|
| A | 8s. | 5s. |
| B | 7s. 9d. | 4s. 3d. |
And it would no longer be to his advantage to exchange either a unit of A (8s.) for a unit of B (4s. 3d.), or a unit of B (7s. 9d.) for a unit of A (5s.). In the first case he would lose a value of 3s. 9d., and in the second a value of 2s. 9d. We see, then, that it might be possible in a loose way to speak of equilibrium if the possessor had no opportunity of exchanging smaller quantities than a pound; but we can also see that the equilibrium is not perfect or symmetrical, for, in the first place, an exchange in the direction of A for B would be more undesirable than one in the direction of B for A; and, in the second place, if we look at our table of marginal values, we shall see that the marginal value of A to the possessor of 4 units is 6s. 4d., whereas that of B to the same possessor, if his supply is 3 units, is only 5s. 10d. This indicates that he would be the gainer by exchanging a little of B, which he values at not perceptibly more than the rate of 5s. 10d., for a little more of A, which he values at not perceptibly less than the rate of 6s. 4d. Let us, therefore, look further into the matter. A
double table (facing p. 70), on the principle of Table I.,
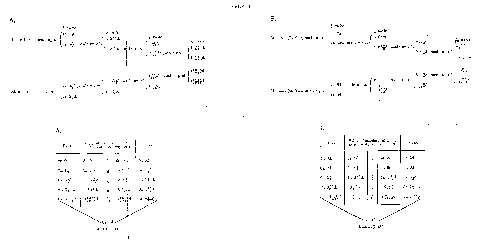
sets forth the fractional values of A round about the margin of four of the units, and of B round about the margin of three. The reader may test the consistency of these data, but will otherwise take them on trust, as before. The 8s. at which the fourth unit of A is estimated is made up of 4s. 5¼d. for the first half and 3s. 6¾d. for the second; and the 5s. at which the fifth pound is estimated is made up of 2s. 9¾d. for the first half-pound and 2s. 2¼d. for the second. If the man possesses 4 units of A, therefore the significance of the last half-unit he possesses will be 3s. 6¾d., and the significance of the next half-unit he would acquire 2s. 9¾d. Similarly, the 7s. 9d. at which the third unit of commodity B is estimated will be found to be made up of 4s. 4½d. for the first half-unit and 3s. 4½d. for the second; and the 4s. 3d. at which the fourth unit is estimated, of 2s. 6d. for the first, and 1s. 9d. for the second. Taking the margin, therefore, at 3 units, the last half-unit possessed will be estimated at 3s. 4½d., and the next half-unit to be acquired at 2s. 6d.; and we shall have—
| Last Half-Unit Possessed. |
Next Half-Unit to be Acquired. |
|
| A | 3s. 6¾d. | 2s. 9¾d. |
| B | 3s. 4½d. | 2s. 6d. |
There is still no advantage to be obtained by exchanging a half-unit of A (3s. 6¾d.) for a half-unit of B (2s. 6d.), or a half-unit of B (3s. 4½d.) for a half-unit of A (2s. 9¾d.), the loss in one case being 1s. 0¾d. and in the other 6¾d., in each case much less than half the loss on exchanging a unit.
If we take ¼ of a unit we shall have—
| Last Quarter-Unit Possessed. |
Next Quarter-Unit to be Acquired. |
|
| A | 1s. 8 5/32d. | 1s. 5 29/32d. |
| B | 1s. 6 27/32d. | 1s. 4 7/32d. |
and still there is no advantage in exchange either way. But if we try 1/8 of a unit we shall have—
| Last Eighth-Unit Possessed. |
Next Eighth-Unit to be Acquired. |
|
| A | 9 201/256d. | 9 57/256d. |
| B | 9 21/256d. | 8 109/256d. |
and we see that there will be an advantage of 36/256d. or 9/64d. in exchanging this increment of B for A.
But if we had only taken 1/16 of a unit we should have had—
| Last Sixteenth-Unit Possessed. |
Next Sixteenth-Unit to be Acquired. |
| 4 1681/2048d. | 4 1303/2048d. |
| 4 937/2048d. | 4 601/2048d. |
and the advantage in the exchange would have been 456/2048d. or 57/256d., which is more than 1/5d., whereas 9/64d. (the advantage in exchanging 1/8 of a unit) is less than 1/7d. Thus we see that though there would be a gain in substituting 4 1/8 of A and 2 7/8 of B for 4 of A and 3 of B, there would be a greater advantage in substituting 4 1/16 A and 2 15/16 B. There is nothing surprising in this. We have often seen that it would be better to make a certain bargain than not, but that it would be better still to make one half of it without the other half. Thus, if the man has 4 of A and 3 of B, it will be better to bargain for an exchange of 1/8 unit of B for 1/8 unit of A than to stay as he is; but if he can make half the exchange instead of the whole, it will be better yet.
A part of the investigation upon which we have been engaged may be illustrated by the accompanying
 diagram, which displays the position of the man who possesses four units of A at a marginal significance of 6s. 4d. and three units of B at a marginal significance of 5s. 10d. It shews how (since the fifth unit of A begins at the same marginal significance as that at which the fourth unit ends, and since this is higher than the marginal significance of the actual supply of B) it follows that even if there is no advantage in exchanging a unit or half a unit of B for A, yet as smaller fractions of the unit are taken, and their values in both cases approach the marginal significances, the time must come when a small fraction of A will be worth more than the corresponding small fraction of B.
diagram, which displays the position of the man who possesses four units of A at a marginal significance of 6s. 4d. and three units of B at a marginal significance of 5s. 10d. It shews how (since the fifth unit of A begins at the same marginal significance as that at which the fourth unit ends, and since this is higher than the marginal significance of the actual supply of B) it follows that even if there is no advantage in exchanging a unit or half a unit of B for A, yet as smaller fractions of the unit are taken, and their values in both cases approach the marginal significances, the time must come when a small fraction of A will be worth more than the corresponding small fraction of B.
But we have not reached a state of equilibrium. All the positions we have hitherto examined leave one of the marginal significances higher than the other. We saw that at 4 A and 3 B the marginal significances are respectively 6s. 4d. for A and 5s. 10d. for B, shewing that a small quantity of B can be advantageously exchanged for A. If we take the marginal values at 4 1/16 of A and 2 15/16 of B we shall find them to be 6s. 1 99/128d. for A, and 6s. 0 83/128d. for B, shewing that a very minute portion of B might still be advantageously exchanged for A. But if we take 4 1/8 and 2 7/8 we shall find the marginal values to be 5s. 11 19/32d. for A and 6s. 3 11/32d. for B, shewing that at these margins a little A might advantageously be exchanged for B. The actual point of equilibrium then lies somewhere between 4 1/16 A and 2 15/16 B, and 4 1/8 A and 2 7/8 B. In other words, to get the maximum advantage the man who has 4 A and 3 B should exchange something more than 1/16 and less than 1/8 of a unit of B for a corresponding fraction of A. On our data it will be found that 1/13 is the precise fraction. The theoretical or absolute marginal value of A at a margin of 4 1/13 is 6s. 1 45/169d., and the marginal value of B at a margin of 2 12/13 is precisely the same. Thus if the man distributes his seven units in any other proportions whatever than 4 1/13 of A and 2 12/13 of B, he would be able to shift them one way or the other with advantage. If they are distributed in this proportion, any change, however small, would involve sacrificing at a little more and acquiring at a little less than the significance of 6s. 1 45/169d. per unit.
So if the man’s supply of the two commodities consisted of seven units, and he were at liberty to exchange them for each other, in units or fractions of units, at par, then whether he began by having seven units of A and none of B, or seven of B and none of A, or some of A and some of B in any proportion whatever, or merely with permission to take out his seven units in whatever way he may choose, he would wind up with as near an approximation to 4 1/13 units of A and 2 12/13 units of B as the fineness of his perceptions and the minuteness of possible division of the commodities allowed. If, on the other hand, he started with the command of five units only he would wind up with 3 units of A and 2 of B at the common marginal significance of 9s. 10d.
For any given command of the two commodities at par, therefore, there is an ideally perfect distribution which gives equilibrium. If the man’s resources are otherwise distributed he is holding something with a lower marginal significance than that of something else that he might have instead of it; and each step he takes to rectify this will raise the marginal significance of the commodity that stands lowest, and lower the significance of the one that stands highest, till the point of equilibrium is reached.
Note, finally, that we have for convenience supposed ourselves to be able to exchange, or otherwise choose between, the two commodities at par, that is unit for unit. If our units are arbitrary we may take the customary unit for A and then fix the unit of B at that quantity (whatever it is) that is offered us as an alternative to it. If we use the customary units for both, then the rates of exchange between them may vary to any extent. But the principle is exactly the same. If the terms on which we may choose between A and B are two units of A to one unit of B, instead of one of A to one of B, then, of course, equilibrium will be reached not when the marginal significance of A, reckoned as a rate per unit, is equal to that of B, but when it is half equal to it, or equal to half of it.
The reader who has followed the investigations with any degree of closeness up to this point will find nothing new in the examples to which we shall now proceed; but if anything remains obscure, tangled, or unstable in his conceptions, these new examples may give him some better power of realising exactly what we have been talking about and may throw back some light upon the ground we have already traversed.
We are still investigating the conception of marginal adjustment and the relation of marginal to total values; and as we have seen
*10 that in ordinary life we seldom or never consider total values with any definiteness, or marginal values except in the close neighbourhood of the actual or contemplated margin of our supply, it will still be necessary to make large claims on the reader’s imagination. Suppose, then, that in a besieged city, or under some merely imaginary circumstances of captivity, or what not, I had the option given me between a quart of water or a (half-quartern) loaf of bread per diem, for a week. If I were wise I should choose the water, for I should certainly have a better chance of surviving, and in any case should die with less suffering, on the water alone than on the bread alone. But if the ratio of a quart of water and a loaf of bread (each to count as a unit) were established, as terms on which I might choose between bread and water, and I were then allowed seven such units for the week, each to be taken in bread or water at my option, the problem of adjustment would become a nice one. I might ultimately choose a pint of water (half a unit) and half a loaf (another half-unit) a day. That would be 3½ quarts and 3½ loaves for the week. What would this mean? It would not, as we have seen, mean that I attach the same value to a pint of water and to a half-loaf in the abstract, or under all conditions; for if I had no provision of either, I should prefer the pint of water. On the other hand, if I had 7 pints of water and 3 loaves for the week, I should, it appears, prefer another half-loaf to another pint of water. The relative values of a pint of water and a half-loaf of bread therefore depend on the supply of each that I already have; and if, being free to subdivide as much as I choose, I arrive at the balance we have supposed, it means that if I had 7 pints and 7 half-loaves for the week I would not exchange the smallest amount of bread for water, or of water for bread, at the rate of a pint of water to the half-loaf. That is to say, the values of bread and water at the actual margins exactly coincide with the terms on which the alternatives between them are offered me. But though they correspond thus at the margins the significance of water rises more rapidly as we depart from the margin than that of bread does. It would be a matter of practical indifference to me whether I lost a very minute amount of water or a very minute amount of bread in the proportion of a quart to the loaf, or a pint to the half-loaf, but it would not be a matter of indifference to me whether I had lost a large part of my supply of water or a large part of my supply of bread in that same proportion. The marginal value of the unit of bread and of the unit of water, then, are the same; but the total value of the water is higher than that of the bread, and the value of any considerable fraction of the water is higher than that of the corresponding fraction of bread. Thus, if my allowance were diminished I should economise more in bread than in water, and if it were reduced very low I should take it all in water. And note also that if the allowance were much increased I should take out most of the increase in water too, for the significance of water not only rises more rapidly than that of bread as we recede towards the first increments, but also, after a time, declines less rapidly as we advance. A loaf a day would be about as much as I should want to eat; but I should always be glad of more water, until I had enough to wash comfortably or even to bathe in. The significance of a pint of water, then, begins at a higher point than that of a loaf of bread. It declines rapidly at first, but after a time very slowly. Whereas the value of a loaf of bread begins lower than that of a pint of water and falls more slowly at first, but after a time declines rapidly, almost abruptly.
We have now seen that if the terms on which bread and water are offered me are a pint to a half-loaf, then, whatever my allowance may be, I shall so distribute it as to bring the marginal significance of bread and water into correspondence with these terms. But what if the terms themselves are changed? What if a pint is to be the equivalent, not of a half-loaf, but a whole one? That is to say, let us suppose that I have now the covenanted right to draw seven pints and three and a half loaves per week, but I may if I like sacrifice a pint for a loaf, or a loaf for a pint, so that if I took it all out in bread I should now have ten and a half loaves a week, and if I took it all out in water, ten and a half pints (five and a quarter quarts). There will no longer be equilibrium at 7 pints and 3½ loaves, for at this margin, as we have seen, it is only just not worth while to buy bread for water at the rate of a pint for half a loaf. Obviously, therefore, it is well worth while to buy it at the rate of a pint for a whole loaf. Only for a small exchange, however; for as I increase my allowance of bread it becomes (perhaps rapidly) less significant to me, and as I decrease my supply of water it becomes more significant to me. So I shall perhaps go no further than exchanging one pint of water for one loaf, and the balance will be struck at six pints of water and four and a half loaves of bread.
If, on the other hand, the terms were changed the other way, and a pint of water would exchange with a quarter of a loaf of bread, so that my whole income would realise 21 pints or 5¼ loaves, I should again alter the distribution of 7 pints and 3½ loaves, but now in the opposite sense; for by sacrificing a quarter of a loaf I could now get a whole extra pint, and seeing that, at these margins, water is only just not worth bread at the rate of a pint for the half-loaf, I shall be glad to secure it at the rate of a pint for the quarter-loaf. But as my supply of water increases, its marginal significance declines, and as my supply of bread is contracted, its marginal significance rises; so that after a slight shifting we should reach a point at which I no longer wish to increase my supply of water at the expense of my supply of bread, even on these improved terms. Perhaps I should not go much further than sacrificing half a loaf of bread to secure two pints more of water, and I might strike the balance at 9 pints and 3 loaves a week.
Thus the proportions in which I devote my resources to either of two alternatives, my tastes remaining the same, depend both upon the terms upon which the alternatives are offered and on the amount of my resources. A change in either of these conditions will affect the distribution.
Next let us imagine a peasant who grows his own foodstuffs and also sells some of his produce. He can get 7s. a cwt. for potatoes and 14s. a cwt. for meal (meal, we will suppose, being the form in which he sells or consumes his grain); and these being the prices, he determines to keep 12 cwt. of potatoes and 10 cwt. of grain for his own use. He might have raised the same sum of money by selling less potatoes and more grain, or
vice versa, and if he had sold more of one he would have held more of the other. In choosing, therefore, as he does, he shews that 12 cwt. of potatoes and 10 cwt. of meal are more valued by him than either 13 cwt. of potatoes and 9½ cwt. of meal, or 11 cwt. of potatoes and 10½ cwt. of meal; for each of these alternatives is open to him, and he embraces neither. We see, then, that he will not forgo half a cwt. of meal for a cwt. of potatoes, nor a cwt. of potatoes for half a cwt. of meal. Now we will suppose that the price of meal and cereals remains constant, but that after our peasant has struck the balance and laid up his provisions for the year the price of potatoes rises from 7s. to 7s. 3d. We will ignore the difference between the buying and selling prices, and will suppose that he can buy back a cwt. of meal on exactly the same terms on which he could have kept it. Now we saw that at the margins of 10 cwt. and 12 cwt. he would neither give a cwt. of potatoes for half a cwt. of meal, nor half a cwt. of meal for a cwt. of potatoes, but it does not follow that he will not give a cwt. of potatoes for half a cwt. of meal plus 3d. The change in the terms may just induce him to make the exchange. Let us suppose that this is so. An advance of 3d., but nothing less, would just induce him to sell a cwt. of potatoes. We might therefore be inclined to say that in that case, since 3d. represents the difference in value to him between a cwt. of potatoes and half a cwt. of meal, it would follow that if potatoes fell to 6s. 9d. instead of rising to 7s. 3d. he would sell a half-cwt. of meal for 7s., buy 1 cwt. of potatoes for 6s. 9d., and secure 3d., which represents the difference between his estimate of the two. But this is a rash inference; for it may be that starting with 12 cwt. of potatoes and 10 cwt. of grain he would find the exchange of half a cwt. of grain for a cwt. of potatoes either more or less distasteful than a change the other way. He requires the premium of 3d. to make him change the potatoes for the grain, but it is possible that he would change the grain for the potatoes for a premium of 2½d., or that he would not do it for less than 3¼d. As in the case of the bread and the water, one of the commodities may rise in significance more rapidly than the other as we recede from the margin, or fall less rapidly as we advance beyond it. But, however this may be, if 3d. just, and only just, induces him to sell 1 cwt. of potatoes, it would require a higher premium to make him sell 2 cwt., for the change from 12 and 10 to 10 and 11 would constitute more than twice the disturbance of the change from 12 and 10 to 11 and 10½.
These examples shew how the original terms on which alternatives are offered to us, or any change in those terms that occurs after we have reached equilibrium, affect or modify our choice. But if free to choose, then whatever the terms may be we can always so distribute or redistribute our resources as to bring the marginal significance of our several commodities into coincidence with them and so reach a true equilibrium; and by doing so we always maximise the desired result.
The art of successful administration consists in so distributing our resources that the marginal significance of all the things we secure corresponds to the terms on which we can get them. These terms may be considered as registering the price we must pay in the sacrifice of any one commodity or satisfaction for the acquisition of any other. Thus they are all connected by a system of external equivalences according to which they may be had in exchange for each other. This we may call the system of their “prices” (in the large sense), measured in each other. And they are all connected by a system of internal equivalences according to which each of them is worth, at the margin, so much of each of the others. This we may call the system of their “worths,” measured in each other. Successful administration of resources brings these two systems into coincidence. It can always do so, for every change of administration modifies the system of worths; it can always be modified in the direction of conformity to the system of prices until it coincides with it; and every such modification increases the volume of desired results, till the coincidence brings it to its maximum.
But we must carry all this further, and must generalise our results. It is not only such things as bread, water, plums, and potatoes that change their marginal value according to the breadth of the supply. I value an extra hour’s leisure in the day, or an extra half or quarter day to my week-end, more or less according to the amount of daily leisure or the amplitude of the week-end. I already enjoy. If I am considering whether I will take a piece of work for which I shall be paid at the rate of 10s. an hour, then (if we neglect the consideration of any irksomeness or any pleasure that the work itself may give me, and look upon the hour simply as subtracted from other occupations) it is easy to see that if I have abundant leisure and am severely straitened for cash, I shall be likely to accept the offer, and if repeated offers come to me I shall go on accepting them. But each successive half-sovereign a week becomes less important, as I am better provided with cash, and each successive hour withdrawn from other occupations involves a greater sacrifice as my reserve of leisure contracts. At last I shall reach the point at which the sacrifice of another hour, at the raised margin, will just compensate the acquisition of another half-sovereign at the lowered margin.
Suppose I can command as much work as I like at 10s. an hour, and I choose to make 250 working days in the year, and to work 6 hours a day, so that I have an income of £750 a year, and suppose I do not care to increase it by £125, at the cost of an extra hour’s work per diem. Perhaps I should be willing to work an extra hour a day if I could thereby raise my income by £250. Suppose, however, that I can command as much work as I like at £1 an hour. If I still work 6 hours a day for 250 days, my income will be £1500 a year. It is possible that I may care to make it £1750 by working an extra hour. It is more likely that I may prefer shorter hours or longer holidays. I might choose to earn only £1000, working 4 hours a day for 250 days, or 5 hours a day for 200. Or it might chance, by a mere coincidence, that I went on working just at the same rate of 6 hours a day for 250 days. That is to say, 10s. at the margin of an income of £750 may have more significance to me than £1 at the margin of an income of £1500, or it may have less, or it may, by a coincidence, have exactly the same. In the first case I should work shorter hours for the higher fee, in the second case I should work longer hours, and in the third case just the same number. But in any case either 10s. or £1 will have more significance at the margin of an income of £750 than at that of an income of £1500.
Similar problems arise apart from money or exchange. The administration of limited resources of space between different claimants is a problem with which every middle-class London householder is acutely familiar. “Can I spare room for it?” or “Is it worth the room it takes?” is often a determining consideration in his selection between alternative possessions. When he gets into the country a man may meet in a pleasanter form the same problem of the administration of space. Can he both have a tennis-court and grow his own vegetables? And if not, which does he prefer? Or if, in any case, he has not room for the tennis-court, how much shall he let his cabbages and lettuces intrude upon his grass plot? Or how shall he settle the rival claims of gooseberry-bushes and rose-trees? The marginal adjustment in such matters may become a problem so delicate that the mind thinks in inches.
Or a young man has made his arrangements to get up at a given hour, to take 30 minutes to dress, 30 minutes for breakfast and the paper, and 30 minutes to walk down to his office or lecture; but when he is called, a new claimant on the time he has so carefully distributed appears, in the shape of the luxury of staying where he is. He remembers hearing that it is bad for the constitution to get up suddenly, and he lies dreamily in bed cutting minutes off one after another of the three assignees of his time, till two-thirds of his resources are exhausted, and he springs out of bed to dress in 10 minutes, to breakfast in 5, and to run down in a quarter of an hour to keep his appointment. The significance of minutes in bed has encroached upon all the others, and by its pressure has revealed the fact that as you cut into them the significance of the minutes assigned to dressing, breakfast, and locomotion, rises unequally. There was a marginal balance at 30 minutes each, but the minutes taken off the time for getting to his appointment rise in significance more rapidly than those assigned to his toilet, and these again more rapidly than those assigned to his breakfast, and when at last these marginal significances, still equal to each other, rise to equality with the now declining value of guilty and uneasy moments in bed, the margins stand, as we have seen, at 5, 10, and 15 minutes. The thirtieth breakfast minute and the thirtieth minute for walking had the same estimated significance, but as you recede the walking minutes rise in value so rapidly that you must go back to the fifth breakfast minute in order to find one as valuable as the fifteenth walking minute.
With time it is natural to associate work, for work involves effort extending over time, and industrial enterprise as a whole may be regarded as aiming at the economical distribution of human effort. At the present stage of our inquiry a hint will be sufficient. We may think of Robinson Crusoe withdrawing a little work in one direction and turning it in another, in order to bring the marginal significance of his products into correspondence with the terms in effort on which nature offers the alternatives to him. Or we may think of our indolent young man, when he has fairly begun his day, carefully considering what expenditure of labour will pay best in the examination for which he is preparing, visited at certain moments by compunction as to the sordidness of this view, and genuinely allured (by the fascination of some subject) into the pursuit of knowledge for her own sake; or fraudulently persuading himself, in another mood, that he has a soul above mere utilitarian considerations, that knowledge of the world is better than University distinction, and that his acquaintance with the modern drama or with the points of dogs or horses is in more urgent need of marginal increments than his knowledge of the niceties of the syntax of a dead language. He too is, wisely or foolishly, administering his resources and endeavoring to bring marginal values into a proper balance with the terms on which alternatives are offered.
Thus the same law holds in intellectual, moral, or spiritual as in material matters. Cæsar tells how when surprised by the Nervii he had barely time to harangue his soldiers, obviously implying that the harangue was shorter than usual. He felt that a few moments, even at such a crisis, were well devoted to words of exhortation to his troops; but their value declined at the margin, and the price in delaying the onslaught rapidly rose; so the moment was soon reached when the time could be better spent than in prolonging a moving discourse. In a story of South America, after the war, we are told of a planter who, when warned by his wife in the middle of his prayers that the enemy was at the gate, concluded his devotions with a few brief and earnest petitions, and then set about defending himself. Had he been a formalist those final petitions would never have been uttered at all; but under the circumstances the impulse to prayer, though sincere and urgent, became rapidly less imperative and exacting relatively to the urgency of taking steps for defence, as the successive moments passed. The most pious biographers of Alfred the Great praise him for “charging like a boar” at the Battle of Ashdown while his brother was still engaged in prayer; and an entirely devout and sincere person may find himself in the dilemma of having either to curtail (or omit) family prayers or to hurry a guest over his breakfast and perhaps run him uncomfortably close for his train. If he shortens, but does not omit, the prayers, it shews that he attaches declining significance to his devotions as minute is added to minute. And in this we shall see nothing ludicrous, as soon as we give up the cant of the absolute in a world in which all things are relative.
We have now abundantly established and illustrated the fact that we administer all our resources, whether of money, space, time, attention, or whatever it may be, upon the same principles.
*11 Our preferences and selections as between two or more alternatives are regulated in every case by the terms on which the alternatives are offered and the supply of the desired things or experiences which we command.
We now know exactly what the marketer is doing, and see that her conduct in the market is regulated by just the same universal principles that regulate her choice between all the alternatives of life. She finds certain prices ruling in the market, and her task is so to regulate her purchases that the last penny spent on beef, apples, potatoes, etc., shall in each case bring equal value, so that a penny withdrawn from any one and expended on any other would be doing a less valued service than it now does. If the prices changed she would get more of one, less of another, none at all of a third, of the things that she buys at present prices, and she would get a little of a fourth that at present prices she does not buy; and in this way she would restore the balance between the marginal efficiencies of the last pennies spent on the several articles. The change in the amounts of every article purchased will be related to the changes in price, but will not be simply proportional to them. A small decline of price in one case will induce a large increase of purchases, and in another a slight one or none at all.
The whole process of marginal adjustment, with the occasional consideration of an “initial” unit (that is to say, the first introduction of “some” as distinct from the modification to “some more” or “some less” of a commodity), is well epitomised and illustrated by the housekeeper who lives in the country, but deals with one of the great London Stores, and who is making out her list. She has a fairly close idea of the extent and distribution of her purchases before she looks at the price list. As she examines the different prices, in making up her order, she half consciously introduces slight modifications, putting down a little more of this and a little less of the other than she had intended, as the prices modify and define her antecedent conception of the terms on which the alternatives would be offered. When she has made up her list and cast up her total, she probably finds that it is too high—that is to say, that to spend so much on the Stores list for the month or the quarter would involve disproportionate pinching in some other spending department. And so she proceeds to revise the list, considering what she can reduce or strike out. The original order was what mathematicians call a first approximation, and now that she is considering what reductions can be made, a closer inspection of marginal values has to be instituted. Some items are struck out altogether. Perhaps they were originally inserted rather in hope than in confidence that they would remain on the effective list. They were “accepted,” but only with a faint chance of being “hung.” The “icing sugar,” for example, that had been inserted with a view to a contemplated birthday cake, goes out bodily, and the order for candied fruits is reduced. Nutmegs (though they have been alleged as an article of consumption not likely to be affected by price) may be taken as exemplifying a kind of commodity that comes under severe review on occasions such as we are now considering; for, as the process of snipping and paring goes on, the small difference in the total reduction of the account which would be effected by the exclusion of the nutmegs altogether may become a determining consideration. During the whole process of this reduction by minuter inspection of the scale of marginal preferences, the housewife will be aware of the alternative in the background of effecting the necessary economies in some other field of expenditure, closely or remotely connected with this. And the yet further question of how much thought and time it is worth while to give, in the hope of making yet further reductions, is meanwhile settling itself under the pressure, high one day and low another, of the competing claims of other duties and pleasures, the resentment or irritation of weariness, or the sudden protest of a roused consciousness that she is in danger of bartering life for half-pennyworths of rice and sugar.
This example will explain why I have occasionally used the cumbrous phrase “the quantity we possess or contemplate ourselves as possessing.” It is clear that the marginal increments or decrements we consider are very often taken not at the margin of our actual possessions, but at the margin of the quantity which we have provisionally determined to acquire, or which, for any other reason, we contemplate ourselves as possessing, and take as the basis of our calculations.
The great principle of the declining significance of successive increments of valued possessions, acquisitions, or indulgences, has now been sufficiently illustrated; but before we can safely go on to the next main point we must say a few words in answer to objections that are frequently urged against the doctrine we have been expounding, and must also make certain explanations. It will be convenient to use the technical term “origin” as a contrast to “margin,” meaning by the “origin” the point at which supplies of anything begin, and by the “margin” the point which they have reached, actually or in contemplation. Thus when we have a small supply of anything the margin will be near the origin, and when we have a large supply it will be remote from it. Now it is not safe to assert that the significance of any commodity declines for successive increments, unless we add the qualification “after a certain point.” It may be that near to the origin the significance does not fall, but rises. We are all familiar with the fact that it is often easier to go without a thing altogether than to have a taste of it and then stop; and many people would prefer no supply at all to a very small supply of something they value.
On the principle that “second helps are never as good as first,” if two slices of pudding given to two children made two first helps they would perform a more important domestic function than if they had both gone to one child and made a first and second help. But if there is only very little altogether, it may be that if divided into two portions it would have teased and stimulated two palates and gratified none. Here the “after a certain point” principle comes in. When single portions to two children would have to be very small, a double portion to one child might be more effective, the second increment in this case being of more value than the first. If the two children are given a share each it will be a wasteful act of administration as far as its direct purpose goes, to be justified, if at all, only by some moral or emotional reaction which the “sharing” itself may be supposed to secure—probably, after all, fostering a certain veiled materialism by over-emphasising such things. A rough system of turn and turn about is probably better husbandry both ethically and materially. This example, in illustrating the “up to a certain point” principle, incidentally indicates the reactions between material and moral problems and considerations, and the general wholesomeness of ethics that are firmly based on sound material administration;
*12 but our main point is to shew that when dealing with small quantities “second helps” may often be better, not worse, than first, and a first and second better than two firsts; so that in any general statement of the doctrine of declining significance with advancing margins the saving clause “after a certain point” must always be inserted or understood.
But even with this qualification the principle is assailed by objections, many of which have already been met by anticipation, but some of which it will be well to consider expressly. It is said, for instance, that though the principle holds for gross material things, each one of which soon produces satiety, yet it does not hold for intellectual or æsthetic satisfactions, nor even for the general command of commodities and services, represented by money. The more a man knows, it is said, the more he wants to know; the more he reads, the more he wants to read; the more music he hears, the more he wants to hear; and very often the more money he has, the more he wants to increase his stock. We will begin with the alleged case of money. It may be true of many men, though it is not true of all, that the more money they get, the keener they are on getting more; but we ought surely to have learnt by this time to be on our guard against vague and indefinite forms of statement concerning matters which are essentially quantitative. The man who has an enormous income may be even keener on “making money” than he was when he was struggling upwards on 30s. a week; but he is not keener on making an extra 1s. a week than he was. He has now no gauge in his mind sensitive enough to feel an addition of £2:10s. to his annual income; and if you ask him to work an extra hour a week, or to incur any appreciable sacrifice, or to put his brains about in any way, in order to secure so trifling a result, he will laugh you to scorn. If you want him to do anything in order to get more money, you must change the terms. There is no such thing as the marginal significance of “money” any more than of “wheat” or of “leisure,” unless both the margin and the unit are stated; and the marginal significance of any specified unit, whether it be 1d., 1s., £1, or £100, has notably declined to this man as his income has risen from 30s. a week to £100,000 a year.
As to the other objections, which refer to intellectual, aesthetic, and other non-material satisfactions, we may note that here again there is a tacit neglect of a principle which must always be assumed when any two sets of conditions are isolated for comparison—the principle, namely, that they must really be isolated; that is to say, that all attendant and modifying circumstances must be supposed to be the same in both cases. Now, if all the circumstances, including the man’s own tastes and capacities for enjoyment, remain the same, then it is as true of concerts as it is of potatoes, that, after a certain point, the greater his supply, the lower will be a man’s relative estimate of the additional services which a further increment will render. If he only has the opportunity of hearing a concert once a month, he may decline an invitation to meet an old friend whom he has not seen for long, and is not likely to see for long again, if the invitation falls on the evening of the concert. Or if he determines to forgo the music, it may be with a distinct consciousness that he is making a serious sacrifice on the altar of friendship. If the same man, with the same tastes and capacities, is hearing a concert every week, he would forgo one with less hesitation and to meet the claims of a lower grade of friendship; and if he is hearing music four days a week he might consider not whether he would sacrifice a single musical evening in order to spend the time with his friend, but how many evenings he could sacrifice before the increasing marginal significance of musical evenings as they become less numerous, and the decreasing marginal significance of evenings with his friend as they become more numerous, reach a balance.
What is really in people’s minds when they say that the more music a man hears the more he wants to hear, is that the man himself will develop fresh faculties and form fresh tastes by cultivation. By going to a concert once a month he may gain such increased knowledge of musical works, and such heightened critical and appreciative powers, that he is now as keen for a second concert in the course of every month as he originally was for a single one. But this is because he is a different man—that is to say, the personal tastes, capacities, and opportunities which affect his whole scale of relative estimates have changed, but it still remains true that, his scale of preferences being what it now is, the significance of a third concert a month is less than that of a second.
The power of appreciating pictures furnishes another good instance. A man who at the beginning of a tour in Italy finds that, in looking at frescoes, the point of diminishing returns is soon reached, and that the value of zero is touched in from a half to three-quarters of an hour, probably finds his powers of enjoyment increasing till his zest remains high hour after hour; but it is still only a matter of time, though now of much more time, before he becomes jaded and requires a period of rest and recovery. Now this reaction of a man’s experiences or volitions upon his character and tastes is a matter of extreme importance, and a careful study of it is necessary to a complete understanding of our whole subject; and accordingly I shall invite the reader in another part of this work
*13 to go into the question at some length and with some minuteness. But what has already been said will probably be enough to enable him to go forward without misgiving to such applications as will be required for the progress of our main argument.
Taking it as granted, then, that there exists what may be called a law of “diminishing psychic returns,” in accordance with which successive increments of any commodity (after a certain point) will render services of decreasing significance to the person who consumes or commands them, let us summarise the results so far obtained in this chapter. To do so will be to repeat in other words the programme laid down on page 80. Given the system of ruling prices, or terms on which alternatives are offered to us, the art of marketing or other expenditure of money is so to regulate the quantities purchased, that the marginal significance of 1d., 1s., or other smallest unit distinguishable in the case in hand, shall secure services of equal value to whatever branch of expenditure it may be devoted. So long as the marginal significances of services rendered by the various commodities do not coincide with their prices, increased satisfactions can be gained by transferring expenditure from the article which has the lower to the article which has the higher marginal significance. And by an extension of terms, which is something more than a metaphor, though something less than a naked statement of fact, we may think of any man who is making a choice between alternatives as going to the great market of nature or of society, ascertaining the terms on which he can make alternative applications of his resources, external or personal, material or spiritual, of money, capacity, influence, and so forth—ascertaining, that is, what are the “prices” that rule in the market of life,—and making his choice accordingly, always adopting the more eligible alternative and so reducing its significance, and neglecting the less eligible and so raising its significance, till their relative importance coincides with the terms on which they can be substituted for each other.
The unity of principle that dominates all administration of resources will become still clearer if we follow up the process that Materfamilias begins in the market-place into the domain of household administration proper. When she has brought home her provisions for the day or week, she is still engaged on the same problem of adjusting marginal significances, in accordance with the law of diminishing psychic returns. The members of the family are not all treated on the same terms. For all kinds of reasons one member of the household will receive differential treatment in one respect, and one in another. It will be regarded as more important that such an one should have a fairly large supply of certain things than that others should have any supply at all. But when a certain amount has been already assigned to the favoured recipient, the marginal significance of further increments for him sinks, till an initial allowance to some one else (though not entering into competition with the initial allowance to him) asserts itself as a rival to his further increments. With this may be compared the case given on page 72 of the initial increments of water being of higher significance than those of bread, and bread becoming an effectively rival claimant at a given point.
The analogy between home administration and marketing becomes yet more striking when we take a single article that has many different applications. Milk furnishes a good example. In the usual routine, milk may be wanted for the baby, for the other children, for a pudding, for tea or coffee, and for the cat. If the supply is at all short, one would be disposed to say that the baby’s wants will be completely satisfied before any others are attended to at all; but even this is not true without qualification. There are circumstances under which, while the baby’s bottle is being filled, one might quite well hear the remark, “Just save a drop for so-and-so’s tea”; and as the proportion of milk to water is, within certain limits, an open question, and as bulk as well as nutritive quality has a certain significance in the economy of the nursery, it is not really so true as one would at first think, that the baby’s wants, to the point of absolute fulfillment, have under all circumstances an unquestioned precedence over all others. And what is not absolutely true of the baby is probably not even approximately true of the other children. They will often go short of what they would like, and of what they would get if milk could be had for nothing. The amount that is to be put aside for other purposes will be more or less carefully considered in determining how much they are to have collectively, and this amount again will be distributed among them individually with more or less care. Even the cat is not dependent on mere superfluity, and her saucer will often be partially or wholly filled with milk that would have been valued in the children’s mugs; though if there is any pressure on the supply and if the other demands have to be arrested at a relatively high marginal significance, her wants may be either neglected or very scantily met, sometimes grudgingly, sometimes with an extra allowance of friendship and sympathy, but still scantily. Milk is administered at home, then, exactly as money is administered in the market-place. The principle in both cases is to bring the marginal significance of small units into equilibrium, at whatever point they are applied; and if a thimbleful of milk has been applied at any one point when it would have met a more important want if applied at another, there has been a failure in the administration of resources, and the administratrix will recognise it by saying, “I wish I had thought of that, and I would have saved a drop of milk for it.”
This brings us to another turning-point in our investigation. Mistakes of administration occur, and a mistake is a mistake. The fact that it need not have been made does not avert its natural consequence. Potatoes run short at table, and there is more cabbage than any one wants to eat. This is the result of miscalculation, and it thwarts expectations. Had a true forecast been formed it would have been easy to pull or buy a cabbage less, and take in or draw from the store another pennyworth of potatoes, and in that case cabbage and potatoes would have run out together, presumably at marginal values approximately corresponding to the prices paid for them. But the fact that we might have had potatoes that we should have valued more instead of the remaining supply of cabbage does not in itself give any value to that remaining supply. This is a very obvious and elementary truth, but if we realise it in all its bearings it will strike at the root of all those “cost of production” theories of value which keep such an obstinate hold on economic thought and are responsible for such endless confusion. The value of what you have got is not affected by the value of what you have relinquished or forgone in order to get it. But the measure of the advantages you are willing to forgo in order to get a thing is determined by the value that you expect it to have when you have got it. If you make a mistake you must bear the loss. You have the thing you bought, not the price you paid for it; and the thing is worth its own value, not the value of something else that you might have got instead of it but did not.
Let us examine this principle further. We have seen, in comparing the different applications of milk in an ordinary middle-class family, that if the administration is ideally carried out, the significance of the last small increments of milk are equal in all its ordinary applications. The first thimbleful of milk given to the baby is immensely more significant than the first thimbleful given to the children or reserved for afternoon tea; but if the last thimbleful given to the cat does not perform as important a service as the last thimbleful given to the children, there would have been a gain in giving her a little less and them a little more; and there has therefore been a failure in administration. The cost of giving more to one applicant is giving less to another, and good administration consists in avoiding any application which costs more than it is worth. But as well as balancing all the uses of milk, at the margin, one against the other, the housekeeper has to balance them all, collectively, against every other alternative expenditure of the money she paid for milk, and this opens up another source of possible mistake. In taking in the milk for the day or half-day the housewife considers, consciously or unconsciously, what the significance of the last thimblefuls applied to all the varied purposes, when properly balanced, will be. The answer to the question, “How much milk shall we take to-day, ma’am?” depends on a rapid survey of the programme of the day. If milk is 4d. a quart, the aim is to take in such an amount that the last half-pint shall be just worth 1d.; that is to say, the last thimblefuls in every application, brought into equilibrium of marginal significance with each other, should collectively be worth just as much as anything else on which the 1d. might be spent. But unforeseen contingencies may arise. There may be a great ink-spill, and milk may be wanted to take out the stain while fresh. A little sapling, laden with many associations, may arrive, to grow in the garden or yard, and some one may have read that milk comforts and revives the roots of trees that have felt a journey. The dog may have eaten phosphorous poison, and some one may know that the proper remedy is to drench him with milk. And these sudden and unexpected claims have not been anticipated or provided for. It may really be the case (especially if you live in the country) that more milk cannot, without great difficulty, be got for some hours; or if you live in the town, it does not occur to you (owing to mental inertia) that there is any way of getting more milk except the customary one of waiting till the milk-man comes round again. And so a new set of claimants on the day’s supply of milk, of which there was no thought when the milk was taken in, has been introduced. In the case of the poisoned dog, it might well be that even the baby would be put on short allowance for a certain period, or driven to some substitute, in the hope of saving the life of an inmate of the house, whose loss would be long and sincerely mourned. Now it may be perfectly understood that there are always such risks, but it is bad economy to provide for a risk as though it were a certainty, and therefore when such a contingency occurs it will set up an urgent demand for which it would not have been reasonable to make provision. It must therefore be met out of the general stock, and all the other uses will be trenched upon. The last thimblefuls will still be kept in equilibrium, but each will meet a more clamorous demand than usual, the lower or less clamorous demands not being met at all; and if the dog has been poisoned, probably the cat will get nothing, even her initial and most urgent claim not being able to compete for a place amongst the higher demands that alone can be satisfied now.
The marginal significance of the last half-pint of milk will be raised above what was contemplated when it was purchased, and it will not be in equilibrium with the marginal pennyworths of other things. Another pint or quart, as the case may be, would have had to be bought to bring down its marginal significance to 2d. a pint; and it would have been bought had the state of things which has actually come about been anticipated. Note the principle, then (obvious indeed in itself and of enormous range of application, but often deeply disguised), that the marginal significance at which a commodity is actually consumed depends upon the urgency and extent of the claims that have to be met and adjusted and the quantity of it at command, and is not affected by the price that was actually given for it. The sacrifice that would be involved in forfeiting a little of our store, and the advantage that would accrue by increasing it a little, depend on how great our store is and what we want it for, not on the importance or value to us of other things that we might have chosen instead of it but did not.
The reverse case to the one we have supposed may also occur. Through an ordinary miscalculation or through some unforeseen change of circumstances, such as the unexpected departure of several members of the household, or the coming on of thundery weather that threatens to turn the milk, the supply for the next few hours may become so much larger than was expected relatively to the demands made upon it, that it will be consumed at a lower marginal significance than would have justified the purchase. The cat may have as much as she chooses to lap. A member of the household, coming in hot from a walk in the sultry air, and expressing a timid desire for a glass of milk, may be treated almost as a benefactor instead of being treated as a criminal, as he was when he last made the same suggestion under less propitious circumstances. And finally, the milk that has gone sour before it is consumed may go to the making of a cake, which, though much appreciated, would not have justified the purchase of the milk to the housewife’s economic mind had she known from the first what it was going to be used for. These marginal applications would not have been deliberately provided for, for their significance is too low to justify expenditure at the rate of 4d. a quart. That is to say, the money spent on the milk might have been used to meet some more urgent want. Only it was not. So here again the price that was actually given for the milk does not determine or affect its significance. An estimate of the probable conditions was made, and such a quantity of milk was taken as would under those conditions have made its marginal significance in all cases just balance that of any other alternative purchase. But if the anticipations are falsified the coincidence will fail. By regulating the supply the marginal significance may be brought into harmony with the price. But the price that has been paid for a faultily regulated supply has no influence on its marginal significance.
Similar considerations, of course, apply to time and work. Perhaps we oftener complain of having wasted time than of having wasted money. We are bitterly conscious of having spent “more time than it was worth” on this or that trifle, and we realise only too clearly that the said trifle is not worth any more because of the precious time that has been spent on it. When our undergraduate is in the examination room, the time he has spent on a branch of the subject on which there happens to be no question avails him nothing, however pathetically anxious he may be to convince himself (and, if it might be, his examiner also) that it does. Anticipated value of information in the examination room determines the amount of time and work he bestows on a subject, but the time and work he has bestowed on it do not determine its value in the examination room. Misdirected effort, however great, secures no marks.
The reader, I repeat, may be surprised at so much insistence on so obvious a fact; but let me warn him once more that this fact, so open and obvious here, will meet him again and again, under deep and subtle disguises, in every region of economic study. He will do well to scrutinise it closely now, in order that he may recognise it whenever he meets it hereafter. If the price that we pay for an article made it marginally worth what we had paid for it—that is to say, if there were any causal connection that made the value at the margin dependent upon the price—then there would be no difficulty whatever in administering our resources; for everything would be worth what we had given for it, just because we had given it, and it would make no difference how our supplies of anything else might stand. Whereas in reality the whole art of wise expenditure consists in deliberately bringing about a coincidence between “price” and marginal significance, which by no means looks after itself, and which will fail if we buy either too little or too much of anything.
And we have seen that the price paid stands for the alternatives forgone; so that ultimately the price we pay for getting this consists in going without that (which we want) or putting up with the other (which we dislike). The principle that we are examining, then, stated in its widest form is that the value of what we have does not depend on the value of what we have relinquished or endured in order to get it. If there is a coincidence, as in a wisely conducted life there will be, it is because the value that we foresee a thing will have determines what we will encounter or forgo in order to secure it, not because what we have encountered or forgone in order to secure it affects its value. If our judgment is bad, our expectations will be falsified and the coincidence will not come about. We do not always like to face this fact, for to do so is to recognise that we have made a mistake; and accordingly we sometimes try to believe that a thing is useful or ornamental because we have given a high price for it, or valuable because we have taken trouble to get it. It is to the housekeeper’s credit if she does not insist on the cabbage that no one wants being consumed with simulated relish, as if it were the potatoes that can’t be had. She is tempted to exact suffering in the shape of enforced consumption to conceal the tragic failure of her attempts to secure satisfaction. But all these plans for concealing the facts do not prevent them from being facts. Efforts are regulated by anticipated values, but values are not controlled by antecedent efforts.
Note, however, that mistakes of calculation are not always irreparable. In the case of rapidly perishable articles such as fish, an over-supply cannot be made use of, because its consumption cannot be spread over a longer period than was originally contemplated without entailing rapid deterioration. And in the case of things which there is only an opportunity of buying at comparatively rare intervals, it may be difficult to remedy an under-supply. But in the case of articles the consumption of which can be spread over a longer or concentrated into a shorter period at will, and the stores of which it is always easy to replenish at any moment, there is no reason why an exact correspondence should not be maintained between the price at which we can get them and the marginal significance at which we consume them. This is no more than to say that in the case of such articles we need never go without a pennyworth that is really worth a penny to us, and need never use a pennyworth to-day when it is only worth a halfpenny, for fear for its being worth nothing at all if we keep it until to-morrow. It must be carefully noted, however, that even in these cases our wise use of the article will be regulated, not by what we actually gave for it, but by what we should have to give for more of it.
There is no doubt a strong tendency in many minds to economise a stock which was bought at a high price, even if it could be replaced at a low one, and perhaps a still stronger tendency to deal prodigally with a stock purchased at a low price, although it will have to be replaced at a high one. But this secondary reaction is recognised as irrational when we deliberately consider it. We know perfectly well that true economy consists in making the best of existing conditions, irrespective of the good or ill fortune, or the wise or foolish conduct, which placed us in them. All these principles will be found presently to have their applications in the commercial and industrial as well as to the domestic world.
sqq.
sqq. The values dealt with in the text may be obtained by integration from the function x
2/2 -7
x + 79/3.
sqq.
x2/2 – 13
x/2 + 125/6.
sqq.
sqq.
