Are instrumental variables (IV) estimates really superior to ordinary least squares (OLS)? Most high-status empirical economists seem to think so. Meta-analyses often treat IV as presumptively superior to OLS. Yet when you ponder IV output, it’s often simply bizarre.
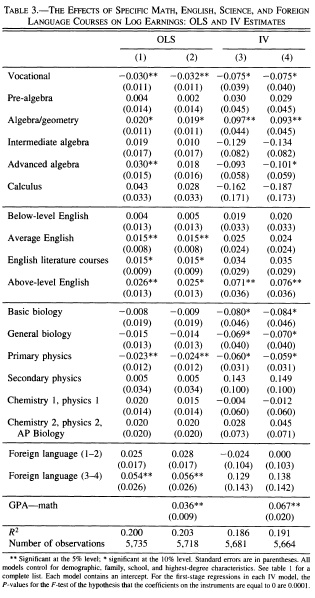
Rose and Betts, “The Effect of High School Courses on Earnings” (Review of Economics and Statistics 2004) is a case in point. The paper’s very good overall. But take a look at their IV estimates for the effect of coursework on earnings. (Columns 2 and 4 adjust for student ability; columns 1 and 3 don’t).
Readers eager to find an effect of curriculum will eagerly point out that the IV estimate implies that algebra/geometry raises adult earnings by 9-10%. But the IV results also imply that advanced algebra reduces adult earnings by 9-10%. (This result is only statistically significant after controlling for ability, but still).
If you look only at point estimates, and ignore statistical significance, the results are even harder to believe. You get big positive effects of secondary physics and third- and fourth-year foreign languages. But you also get a massive negative effect of calculus. Calculus!
You could accuse me of cherry-picking (lemon-picking?) some exceptionally odd IV results. But in my experience, Rose and Betts is typical. And if published IV results are implausible, the unpublished results are probably far worse.
A staunch empiricist could admittedly object that we shouldn’t call statistical output “bad” merely because it contradicts our theories. I’d reply, though, that “IV estimates are better than OLS estimates” is itself a theory. The main way to test this theory is to race IV versus OLS on questions where we are already confident that we know what the right answer is (or at least what the wrong answer is). By that standard, the privileged status of IV seems unjustified.
Please share your dirty laundry about instrumental variables in the comments. To avoid confirmation bias, please also share your clean laundry. 🙂

READER COMMENTS
JFA
May 22 2013 at 12:47am
IV regressions are only as good as the IV itself. If the instrument is weak (i.e. is valid but explains little of the endogenous variable) then results may (will?) be worse (what does that exactly mean?) than OLS. If you have endogeneity (large endogeneity?) in one of your explanatory variables, then the issue of OLS being better than IV makes no sense, since OLS will not give correct results either.
Bill Conerly
May 22 2013 at 1:12am
When I started my first corporate job, I looked at a forecasting model estimated in OLS and started re-estimating with two-stage. The “new and improved” version looked pretty much like the old one and gave very similar forecasts. So a colleague asked, “What did we gain from this exercise?”
Tony
May 22 2013 at 1:59am
I like this post a lot. It raises some interesting questions about when to use OLS versus IV. It also got me to read that Rose and Betts paper, which was fun.
That said, I have a couple of observations:
Given these previous two points, trying to argue against “IV is morally superior” by saying that “OLS is better on average” is likely to run into trouble. I think a more effective argument is to argue that there are an economically significant # of times that OLS > IV. This strikes me as true (see Jaeger, Bound, and Baker).
[comment html fixed–Econlib Ed.]
Hendrik Juerges
May 22 2013 at 2:30am
Sorry, but from your example one does not even know what is the endogenous regressor and what is the instrument.
Doug
May 22 2013 at 3:44am
In any statical learning context it’s impossible to classify one algorithm as inherently “superior” to another. It depends on the nature of the data. For some data sets OLS will outperform IV, for others vice versa.
It’s the responsibility of the practitioner to understand the subtleties of the data and pick the superior method.
http://en.wikipedia.org/wiki/No_free_lunch_theorem
Eric Falkenstein
May 22 2013 at 9:56am
I think IV is a too-clever way to address an omitted variables bias. Think of it this way: have you ever seen a compelling IV regression that couldn’t be presented as an OLS after suitable adjustment of the independent variables?
As per crazy coefficients, this is from the correlations between inputs and their nonlinear effects on the output. As you note, they imply patently absurd causation stories. I’ve found that nonlinear effects of independent variables often generates ‘wrong-sign’ coefficients of high significance when they are presented with other highly correlated inputs in linear regressions.
Jason Sorens
May 22 2013 at 10:04am
Unlike OLS, IV is always biased. Under some conditions, IV can be less biased than OLS. Yet the exclusion restrictions for IV are extremely tough, and much empirical work does not properly evaluate them (although economists have been better at this than political scientists — I’m not sure I’ve ever seen Stock and Yogo cited in a political science paper).
And I’ll also second what Eric Falkenstein writes here: “I’ve found that nonlinear effects of independent variables often generates ‘wrong-sign’ coefficients of high significance when they are presented with other highly correlated inputs in linear regressions.” In these cases, a very small number of observations can be driving sign switches. For the vast majority of observations, then, plausible substantive estimates need to combine coefficients on the correlated variables.
David Jinkins
May 22 2013 at 10:08am
I agree with JFA. The problem with empirical economics is that we generically only have observational data to work with. OLS can tell us about correlations in data, but won’t be able to say much about causality. IV regressions turn observational data into a pseudo-experiment.
For example, suppose that we had data on courses taken and earnings, as in the study you cite above. Suppose simple OLS told us that people who take math courses earn more. That is fine as far as it goes, but we really want to know if it is just that smarter people take math courses, or that the math course itself increases earnings. OLS isn’t going to help, but a good IV will.
Suppose that due to a bad pineapple, the pina colada mix at a mathematics department picnic in one high school was poisoned. Half of the mathematics faculty was laid up in the hospital for a semester. Many planned math courses were not offered that year. Presumably, the only way the pina colada disaster affected the future earnings of students is through the courses they were able to take. The exogenous variation in mathematics courses available creates the equivalent of an intent-to-treat experiment. Even the smart students were less likely to take math courses during the pina colada year.
Now, as in any statistical procedure, garbage in, garbage out. If the IV is invalid or weak, then the result of the IV regression is totally meaningless. Maybe that is the case in the study you cite — I didn’t read it.
Yodde
May 22 2013 at 10:17am
Never been a big fan of IV, despite its high status among economists over the past 20 years. Exogeneity does not exist in the real world, and IV typically introduces more problems than it solves, particularly in cases where measurement error is endemic (which is to say, most of economics).
In my view, IV is popular not because it is a great way to get at the truth, but instead because it elevates the status of the econometrician from being basically a computer programmer up to being a creative genius in pursuit of clever instruments. One can think of several top empirical researchers in economics who have made their names not for really learning anything about the world, but for identifying clever instruments.
Daniel Kuehn
May 22 2013 at 11:03am
In practice IV is often very bad, I agree. I don’t think that’s a good reason to just embrace OLS, though. It’s a reason to spend a lot more time looking for good discontinuities and natural experiments that are much clearer as a strategy for identifying the model.
OK my story – relatively early on in my time at the Urban Institute I somehow got a paper accepted to an IZA conference on the economics of youth risk-taking behavior. We did some relatively non-exotic modeling our paper. I was one of only two people there that didn’t use an IV strategy of some sort (and by far the youngest one). It was very intimidating at first but in the end no one believed anyone else’s IV anyway and everyone believed their own IV, so I didn’t feel all that bad. My paper wasn’t as fancy but it was definitely no less convincing to the average attendee than anyone else’s there.
Moral of the story is I think people are skeptical of IVs in general and that’s probably a good thing. They persist because the identification problems that they’re there to solve are very real and very problematic.
JFA
May 22 2013 at 12:04pm
@ Jason Sorens: “Unlike OLS, IV is always biased”??? If there is an omitted variable, OLS will be biased; that’s exactly why researchers came up with IV. As long as the instrument is not correlated with the error term, the beta_IV is unbiased. Granted, this is from the asymptotic perspective and finite sample properties may lead to bias, but one should probably weight mean squared error more than whether the coefficient is unbiased. If a researcher thinks there is significant endogeneity (because there will always be endogeneity) then the researcher should not trust the OLS estimates. That being said, there may also not be a good instrument, so IV results may not be reliable either. A researcher should probably just go with a Bayesian approach, explicitly stating her priors rather than bringing them through the back door.
Jason Sorens
May 22 2013 at 12:46pm
JFA: If there is an omitted variable that is correlated with both an independent variable and a dependent variable, OLS is biased & inconsistent. IV is always biased in finite samples unless the instruments are perfectly strong, which is never the case in real work. If the instruments satisfy the exclusion restrictions well enough, then IV is indeed less biased than OLS — but it’s still biased.
JFA
May 22 2013 at 1:24pm
@ Jason: You’re correct… my mistake… I was thinking consistency.
Doug
May 22 2013 at 5:11pm
Commenters are trying to argue that one regression is better than the other based on which has more bias.
This isn’t directly relevant to out-sample performance of the regression. For example Lasso regression can exhibit very high bias, but often outperform OLS.
Staunch Empiricist
May 23 2013 at 12:58am
Wait, why are we ignoring the significance again..?
Sure, the sign on calculus is negative, but it’s not significant.
The sign on advanced algebra is also negative, but it’s *barely* significant at the 10% level (and insignificant at the 5% level).
Given the (lack of) significance, isn’t the paper overall kind of plausible?
Couldn’t it just be that this paper is looking at ~20 variables, so some of these signs really are just flukes, and not at all/barely significant flukes at that?
The real danger with IV would seem to be the same problem with all probabilistic (non-Bayesian) methods, which is that you can run several dozen regressions, pick up a significant finding purely by chance, and publish the result. But that is a problem with lots of methods, not just IV, including (especially?) OLS.
The cure, of course, would be Bayesian reasoning. Use lots of different methods (including lots of different IVs, why not?), build up a nice big literature, and then adjust your point estimates accordingly over time. Don’t just rely on one paper, let alone one single IV.
Staunch Empiricist
May 23 2013 at 1:04am
PS – Do economists tend to rely on single papers (based on IV)? I know the media does, I know politicians do too, some motivated think tanks do too, but do lower-case-s serious economists as a group tend to look at a single IV result and take it very seriously?
(Daniel Kuehn’s story would seem to suggest the answer is “no, except when it’s *my* IV,” but I am genuinely asking…)
James Bailey
May 23 2013 at 2:17am
Well, we know IV is less efficient than OLS.
Mike Rulle
May 23 2013 at 5:30pm
My comment here is really a parenthetical.
It is very possible that meta-studies produce exact opposite outcomes than they purport to produce. I have a bias. My bias is that studies which do not produce something close to a rejection of the “null” are published less frequently. Further, my bias is that “researcher bias” tends to produce lower p-values on average than if such bias did not exist.
Given my “priors”, all meta studies do is increase “N” and thus produce lower p-values. This may give the false impression there is more validity to the individual studies inside the meta study—which is impossible to know one way or the other. They also cannot add to the size of the experimental values—-just their “significance”.
Like anyone else, I look at meta study results—as the theoretical logic is good. But I prefer using it when I know how the studies were done in the meta-analysis.
Comments are closed.