Does a referendum represent “the will of the people”? What if this will can change even if nobody’s will change among the people? Can the British Parliament produce inconsistent votes even if no Member of Parliament changes his mind? The Economist writes:

Politicians on both sides of the Brexit divide talk sanctimoniously of the “will of the people.” … In truth, the will of the people is decidedly muddy, declares Sir John Curtice in his latest report for NatCen Social Research, based on survey data collected in early February.

Jean-Antoine-Nicolas de Caritat, marquis de Condorcet, was an 18th-century mathematician, philosopher, and classical liberal who gave his name to the “Condorcet paradox.” His discovery, replicated and expanded by mathematician Charles Dodgson (a.k.a. Lewis Carroll) in the 19th century and economists Duncan Black and Kenneth Arrow in the 20th, is often ignored in attempts to understand political decisions. (See my “The Vacuity of the Political ‘We’,” Library of Economics and Liberty, October 6, 2014.) Yet, I just discovered on the web many discussions of the Condorcet paradox and Brexit: just google it—or continue reading this post.

The Condorcet paradox can lead the British electorate (or their MPs) to both want and not want Brexit. Consider the following illustration.

Imagine three alternatives: a hard Brexit (H), a soft Brexit (S), or remaining in the European Union (R). Suppose the British electorate is composed of three groups each sharing the same preferences among the three alternatives. No group reaches 50% of the electorate, but they can be close, and one group can be very small. The chart below depicts these alternatives with ordinal utility indices on the vertical axis (a higher number representing a more preferred option). A description in English:

  • Each individual in Group A, we suppose, prefers H to S to R, which we can write as H>S>R. (I use the symbol “>” to mean nothing else than “preferred to.”) You can view these individuals as the Brexiters.
  • Each individual in Group C prefers R, but would still choose H as his second option—perhaps because he dislikes wishy-washy solutions and political uncertainty. So, for Group C, R>H>S. You may think of these individuals as eccentric Remainers (but the main point is to show the possibility of the Condorcet paradox with different individual preferences).
  • For each individual in Group B, S>R>H. Think of them as middle-of-the-road centrists tempted by Brexit.

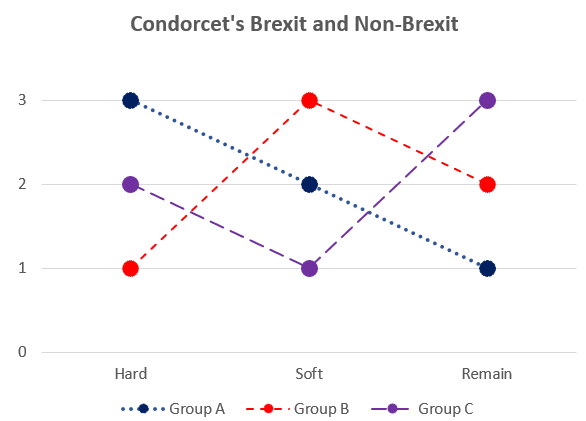
An illustration of the Condorcet paradox as it may apply to the Brexit-Remainer debate. By Pierre Lemieux.

Imagine that this electorate is called to vote on H and S. Group A and group C individuals will vote H, and S will be defeated. We may say that the electorate prefers H to S, and write this as H>S, the bold characters indicating that we are considering the whole electorate instead of a section of it. If the electorate is called instead to choose between S and R, S would win, thanks to the votes of groups A and B. So, S>R. If the electorate is rational in the sense that its preferences are transitive, these two results imply H>S>R, that is, H>R.

Let’s now ask our electorate to vote on H and R. The surprise is that the vote would give a majority to R, that is, R>H, because that’s what groups B and C would choose. This is the essence of the Condorcet Paradox: despite all voters having transitive preferences, the electorate prefers both H to R and R to H. The “will of the people” is incoherent.

After he independently rediscovered the Condorcet paradox, Duncan Black recalled that “[his] stomach revolted in something akin to physical sickness.”

The same paradox can mar the decisions of any committee or assembly (including the British Parliament), although the more numerous and diverse the voters are, the more chances the Condorcet paradox will pop up. Also, the more alternatives are presented to the voters, the more likely the paradox will materialize. So it may very well be the case that, if only for that mathematical reason, the British electorate wants both Brexit and full membership in the European Union.

A dozen years ago, I devised a little economic exercise on the Condorcet paradox showing how, in the same vein, Quebecers might want, literally, an independent Québec in a united Canada.