Studies in the Theory of International Trade
By Jacob Viner
In this book I first endeavor to trace, in a series of studies of the contemporary source-material, the evolution of the modern “orthodox” theory of international trade, from its beginnings in the revolt against English mercantilism in the seventeenth and eighteenth centuries, through the English currency and tariff controversies of the nineteenth century, to its present-day form. I then proceed to a detailed examination of current controversies in the technical literature centering about important propositions of the classical and neo-classical economists relating to the theory of the mechanism of international trade and the theory of gain from trade. The annual flow of literature in this field has become so great in the last few years, and the claims on my time and energy from other unfortunately unavoidable activities of a quite divergent sort have been so heavy, that the completion of this book and the rendering of full justice to the recent literature have proved to be incompatible objectives. I hereby present my sincere apologies to the substantial number of economists who have in recent years made valuable contributions to the theory of international trade which are here either wholly neglected or treated more summarily than they deserve…. [From the Preface]
First Pub. Date
1937
Publisher
New York: Harper and Brothers Publishers
Pub. Date
1937
Copyright
The text of this edition is under copyright. Picture of Jacob Viner courtesy of the University of Chicago Department of Economics.
Chapter IX
GAINS FROM TRADE: THE MAXIMIZATION OF REAL INCOME
It is the mark of an educated man to look for precision in each class of things just so far as the nature of the subject admits; it is evidently equally foolish to accept probable reasoning from a mathematician and to demand from a rhetorician scientific proofs.
—Aristotle, Ethica Nichomachea, 1094 b, as cited by T. V. Smith, International Journal of Ethics, XLVI (1936), 385.
I. “MASS OF COMMODITIES” AND “SUM OF ENJOYMENTS”: RICARDO AND MALTHUS
In the comparative-cost approach to the problem of gain from foreign trade, the stress is put on the possibility of minimizing the aggregate real costs at which a given amount of real income can be obtained if those commodities which can be produced at home only at high comparative costs are procured through import, in exchange for exports, instead of being produced at home. In the later development of the theory of international trade, several methods of dealing with the income aspects of foreign trade are introduced, and in the exposition of Marshall and Edgeworth, though the comparative costs are still a factor in the situation,
*1 they appear in the analysis only implicity through their influence on the reciprocal-demand functions, which, in so far as they are
welfare functions, represent “net” income or income-minus-cost quantities.
Ricardo and Malthus, in the course of a discussion of concrete problems of trade policy, offered some indication of the nature of the “welfare” presuppositions of their gain analysis. In Mill, Marshall, and Edgeworth these presuppositions are left unexpressed, as far as their international-trade analysis is concerned, and must be inferred from their other writings. As will perhaps be made evident, it is a question whether Marshall and Edgeworth, notwithstanding their more elaborate techniques of analysis, improved substantially upon what Ricardo and Malthus said, scanty though that was, with respect to the criteria of gain or loss from foreign trade.
Malthus attributed to Ricardo—whether rightly or wrongly is open to argument—the position that the saving in cost under free trade resulting from obtaining the imported commodities in exchange for exports instead of by domestic production not only demonstrated the existence of gain from trade but measured the extent of the gain. To this proposition Malthus objected that the excess in the cost of domestic production of the imported commodities over the cost of obtaining them in exchange for exports provided a grossly exaggerated measure of the gain from trade where the imported commodities could not be produced at home at all or could be produced only at extremely high costs.
*2
Mr. Ricardo always views foreign trade in the light of means of obtaining
cheaper commodities. But this is only looking to one half of its advantages, and I am strongly disposed to think, not the larger half. In our own commerce at least, this part of the trade is comparatively inconsiderable. The great mass of our imports consists of articles as to which there can be no kind of question about their comparative cheapness, as raised abroad or at home. If we could not import from foreign countries our silk, cotton and indigo…with many other articles peculiar to foreign climates, it is quite certain that we should not have them at all. To estimate the advantage derived from their importation by their cheapness, compared with the quantity of labor and capital which they would have cost if we had attempted to raise them at home, would be perfectly preposterous. In reality no such attempt would have been thought of. If we could
by possibility have made fine claret at ten pounds a bottle, few or none would have drunk it: and the actual quantity of labor and capital employed in obtaining these foreign commodities is at present beyond comparison greater than it would have been if we had not imported them.
Malthus held that the gain from trade consisted of “the increased value which results from exchanging what is wanted less for what is wanted more”; foreign trade, “by giving us commodities much better suited to our wants and tastes than those which had been sent away, had decidedly increased the exchangeable value of our possessions, our means of enjoyment, and our wealth.”
*3 Malthus, here as elsewhere, meant by “value” or “exchangeable value” not value in terms of money but purchasing power over labor or “labor command.” He reached the conclusion that foreign trade increases the sum of “labor command” in the following fashion: foreign trade, when it results in a new assortment of commodities available for use which is “better suited to the wants of society” than the pre-trade one, increases income in the form of profits without a proportionate decrease in other forms of income, and therefore increases the amount of money available for payment as wages, or the demand for labor; wages do not rise in proportion to the rise in total money income; therefore the new income constitutes a greater sum of “labor command” than the old one.
*4 Malthus would, therefore, presumably deny that there was gain from foreign trade if money wage rates rose relatively as much as total monetary income, so that there was no increase in “labor command.” To measure gain by the increase in “labor command” without reference to the terms on which labor can be commanded is a fantastic procedure if laborers are recognized as constituting part of the population.
Malthus would have done much better if he had stopped with the exchange of “what is wanted less for what is wanted more” as constituting the content of the gain from foreign trade. He got into this muddle in an attempt to rebut the proposition with which Ricardo’s famous chapter on foreign trade opens: “No extension of foreign trade will immediately increase the amount of value in a country.”
*5 Malthus regarded this as an absurd proposition,
whereas if he had ever succeeded in mastering Ricardo’s peculiar use of terms he would have seen that it was a sterile truism. Ricardo’s proposition rests upon his use of the quantity-of-labor cost as the measure of value and upon his tacit assumption that foreign trade influences what labor shall produce but does not affect immediately how much labor shall be engaged in production.
Ricardo, however, did not measure gain by changes in “value” as defined by him, and therefore did not deny that foreign trade resulted in gain. After laying down his proposition that foreign trade will not immediately increase the amount of value in a country, Ricardo went on to say that “it will very powerfully contribute to increase the mass of commodities, and therefore, the sum of enjoyments.”
*6 What was intended by Ricardo as the main proposition was, at least for our present purposes, of no importance. The incidental comment, on the other hand, was of great importance. It suggests two income tests of the existence, and perhaps also two income measures of the extent, of gain from trade, namely, an increase in the “mass of commodities” and an increase in the “sum of enjoyments.” Ricardo did not expand these suggestions, but in his
Notes on Malthus he repeated them: if two regions engage in trade with each other “the advantage…to both places is not [that] they have any increase of value, but with the same amount of value they are both able to consume and enjoy an increased quantity of commodities,” adding, however, that “if they should have no inclination to indulge themselves in the purchase of an additional quantity, they will have an increased means of making savings from their expenditure.”
*7
Both types of test, needless to say, involve in their application serious logical or practical difficulties. The “mass of commodities” is significant only as it is accepted as a measure or index of the “sum of enjoyments” and the “sum of enjoyments” is not itself directly measurable. The use of “mass of commodities” as a measure of gain from trade, or even as an index of the direction of change, would involve in practice the use of an index number of national real income. As in the case of the measurement of real
costs, the determination of the proper weights for the quantities of different commodities presents serious, and in strict theory insoluble, problems. There is no evidence that Ricardo gave any thought to these problems. Malthus, however, in defending his own “labor command” test, succeeded in locating the most vulnerable point in the “mass of commodities” test. Where the commodities imported were such as in the absence of foreign trade could not have been produced at home, or could be produced only at prohibitively high costs, Malthus objected, “we might be very much puzzled to say whether we had increased or decreased the quantity of our commodities,”
*8 presumably because after trade the country would have more of the imported but less of the native commodities than before trade with no means available of comparing
exactly the amount of increase in the one with the amount of decrease in the other.
Malthus could have gone further: even if there were more of
every commodity after trade as compared to before trade, the removal of the duties would certainly have resulted in an increase in the quantity of commodities in any physical sense, but there would not necessarily have been an increase in real income or in “sum of enjoyments.” The argument should scarcely call for elaboration. The removal of duties tends to alter the distribution of the national money income unfavorably for the owners of the services entering relatively more heavily into the production of the hitherto protected commodities than into the production of the export commodities. The removal of duties tends also to raise to domestic consumers the prices of the export commodities relative to the prices of the hitherto protected commodities. Suppose that labor enters relatively more heavily into the production of the protected commodities than into the production of the export commodities, and that labor is a heavy consumer of the export commodities but a light consumer of the protected commodities. The removal of the duties, therefore, operates injuriously to labor in two ways: it lowers the relative share of labor in the national
money income, and it raises the prices, relative to other commodities, of the things on which labor spends its wages. It is still
possible that labor may gain from the removal of the duties, for under the conditions given it is still possible for the buying power of money wages over the things laborers buy to be greater after the removal of the duties than before. Even if labor does lose, other classes will necessarily gain more than labor loses in physical income, if in measuring physical income the quantities of particular commodities are weighted for purposes of summation by their prices under free trade, or their prices under protection, or any
intermediate scale of prices, and if the import duties were not merely nominal but were actually restrictive of import of the dutiable commodities.
*9 But if labor is relatively a low-income class, the removal of import duties might result in a loss of physical income to labor which, weighted by its utility coefficient, might conceivably be greater than the gain in the physical income of the other classes, similarly weighted by its utility coefficient. It is possible, therefore, that even with the usual abstractions from short-run immobilities and rigidities, from monopoly conditions, and from changes in aggregate real cost on the production side, free trade may result in an impairment of psychic income. But the combination of adverse circumstances necessary to produce this result is so formidable as to justify the conclusion that there is ordinarily a strong presumption that free trade—given the usual long-run assumptions—will increase the national real income. Economic analysis can here at best yield only strong presumptions, but this limit in the power of economic analysis extends to the entire field of welfare analysis.
Haberler, on the basis of a combination of
a priori and empirical considerations, claims that in the long run the functional distribution of real income is unlikely to be appreciably different under free trade than under protection, and that in so far as it would change with the adoption of free trade the change would more probably be favorable than unfavorable to labor. Free trade, he argues, will result in a rise in the real prices of those factors which are “specific to” the export industries; it will result also in a rise, though a lesser one, in the real prices of non-specific
factors; and it will result in a fall in the real prices of those factors which are specific to the protected industries which must reduce their operations or disappear under free trade. Labor is in the long run the least specific of all factors. It will therefore be in the intermediate position, and will gain from the general increase in productivity.
*10
While Haberler’s conclusions may be sound, this reasoning seems inadequate justification for them. Haberler uses “specific” to mean occupational immobility, whether due to technical or to other causes. He compares the mobility of only labor and “material means of production,” which latter is scarcely an elementary factor of production. Natural resources of the agricultural or mining type are no doubt the most specific of the factors, but in the long run it would seem to be free capital and not labor which is the least specific. In any case, it would seem to be not occupational mobility in general, but occupational mobility as between the tariff-sheltered and the unsheltered industries which would be of primary significance for this problem. If labor was used relatively heavily by the protected industries, relatively lightly by the unsheltered industries, and if its marginal productivity decreased slowly in the former and rapidly in the latter as more labor was employed while the other factors were held constant, the removal of tariff protection would lessen the relative share of labor in the national money income. I see no
a priori or empirical grounds for holding this to be an improbable case. But even if labor on the average had low occupational mobility and were employed relatively heavily in the protected industries, its real income might still rise with a removal of tariff protection even though its money income and its relative share in the national money income and the national real income all fell, if it was an important consumer of the hitherto protected commodities, and if the prices of these commodities fell sufficiently as a result of free trade to offset the reduction in money wages in the new situation.
The concessions made above to the protectionist case do not qualify the conclusion that free trade—given the usual assumptions—necessarily makes
available to the community
as a whole a greater physical real income in the form of more of
all commodities, and that the state, if it chooses, can, by appropriate
supplementary legislation, make certain that the removal of duties shall result in more of
every commodity for
every class of the community. When the Cobden Treaty was negotiated, Proudhon complained that while it admittedly made cottons cheaper and more abundant in France, it made wine dearer and scarcer, and that the French masses lost more from the latter consequence of the treaty than they gained from the former. It cannot be said with confidence, on
a priori grounds alone, that Proudhon was mistaken. But the French government could have brought it about that the Cobden Treaty should not result in a reduction in wine consumption in France—or by any stratum of the French population—by levying special income taxes on the class which consumed cotton goods relatively most heavily and using the proceeds to subsidize the class which consumed wine relatively more heavily, or by levying
internal consumption taxes on cottons (at lower rates than the effective amount of the import duties which had been removed) and using the proceeds as a subsidy to domestic wine consumption, or by some other stratagem of this general character, designed to offset an undesired effect of the reduction of duties on the distribution of the national income.
Free trade, therefore, always makes more commodities available, and, unless it results in an impairment of the distribution of real income substantial enough to offset the increase in quantity of goods available, free trade always operates, therefore, to increase the national real income. That the available gain is ordinarily substantial there is abundant reason to believe, but the extent of the gain cannot in practice be measured in any concrete way. These conclusions, which are little more than a paraphrase of some words of Cairnes’s,
*11 are, in my opinion, very nearly as far as the argument can with advantage be carried. The remainder of the chapter is devoted to an examination—as sympathetic as I can make it—of the more elaborate methods of analysis by which J. S. Mill, Marshall, Edgeworth, and others obtained results which were, seemingly at least, more precise and conclusive, with respect to the income gains from trade.
II. RECIPROCAL DEMAND AND THE TERMS OF TRADE
From the time of Ricardo on, the commodity terms of trade have been widely accepted as an index of the trend of gain from trade. Some writers have also derived a measure of the ratio in which the gains from trade were divided between two trading areas from their commodity terms of trade taken in relation to the comparative costs of production of the two areas. In earlier chapters the terms of trade have been dealt with merely as manifestations of certain objective price relations, without reference to their gain significance. Before proceeding to an examination of the validity of the use of the terms of trade as an index of gain, it is necessary to consider further the objective relationship of the terms of trade to other international trade phenomena, and especially the connection between the “reciprocal demands” and the commodity terms of trade. Analysis of this connection begins with Torrens and John Stuart Mill. Marshall and Edgeworth later made it a field for the exercise of their geometrical skill, but admittedly without departing substantially from J. S. Mill’s mode of approach or conclusions. While a number of writers have reproduced their analysis in sympathetic fashion, Graham alone has subjected it to really severe criticism. This section, therefore, will be confined to an examination of the contributions of Mill, Marshall, and Edgeworth, with reference at appropriate points to Graham’s criticisms. Since the original sources are all readily available, the summaries presented here will be restricted to the minimum necessary to afford a sufficient basis for appraisal of their techniques of analysis and their most general conclusions.
John Stuart Mill.
Mill’s discussion of the relationship between reciprocal demand and the commodity terms of trade was in the main a pioneer achievement, and probably constitutes his chief claim to originality in the field of economics.
*12 The problem
for which Mill seeks an answer is the mode of determination of the commodity terms of trade. He first simplifies the problem by assuming only two countries and only two commodities.
*13 Mill held that the equilibrium terms of trade must be within the upper and lower limits set by the ratios in the respective countries of the costs at which the two commodities could be produced at home, but that the exact location of the terms of trade would be determined by the demands of the two countries for each other’s products in terms of their own products, or the “reciprocal demands.”
*14 Equilibrium would be established at that ratio of exchange between the two comodities at which the quantities demanded by each country of the commodities which it imports from the other should be exactly sufficient to pay for one another, a rule which Mill labels the “equation of international demand” or “law of international values.”
*15
Shadwell later objected that Mill had not really solved the problem by his “equation” or “law,” but had merely stated the truism that “the ratio of exchange is such that the exports pay for the imports,”
*16 and Graham makes substantially the same criticism.
*17 Except for the case of pure barter, however, there is nothing “truistic” about the equality in value of imports and exports, and in fact they would ordinarily not be equal even after allowance for “invisible” items if, as is proper for present purposes, money and the money metals were not counted as exports or imports. It
would be true, however, that Mill would not have accomplished very much if he had merely established the necessity under equilibrium of equality in value between imports and exports. But as Bastable pointed out in reply to Shadwell, “Mill’s theory does not consist merely in the statement of the equation of reciprocal demand, but [also] in the indication of the forces which are in operation to produce that equation.”
*18 The terms of trade, according to Mill, are determined by the reciprocal demands, conceived in the schedule or function sense, subject to the condition that imports shall equal exports in value. A fair reading of Mill’s chapter warrants no other interpretation. There is, moreover, supporting evidence for this interpretation. Mill, as we have seen, stated that “This law of international values is but an extension of the more general law of value, which we called the equation of supply and demand.” To what appears to have been a criticism similar to Shadwell’s made by Cairnes against Mill’s use of the analogous “equation of supply and demand” in his general value theory, Mill replied:
*19
I think that the proposition as laid down [i.e., “the equation of supply and demand”] is something more than an identical proposition. It does not define—nor did it, as I stated it, affect to define—the causes of variations in value. But it declares the
condition of all such variations and the necessary
modus operandi of their causes, viz., that they operate by moving the supply to equality with the demand or the demand to equality with the supply.
To explain the determination of the terms of trade by reciprocal demand and the “equation of international demand” Mill used arithmetical illustrations. It is not surprising, therefore, that his results had sometimes a more restricted range of validity than he appeared to recognize. But the following summary and graphical illustration of his results in one of his hypothetical
cases
*20 may serve, nevertheless, to reveal the pioneer character of his analysis.
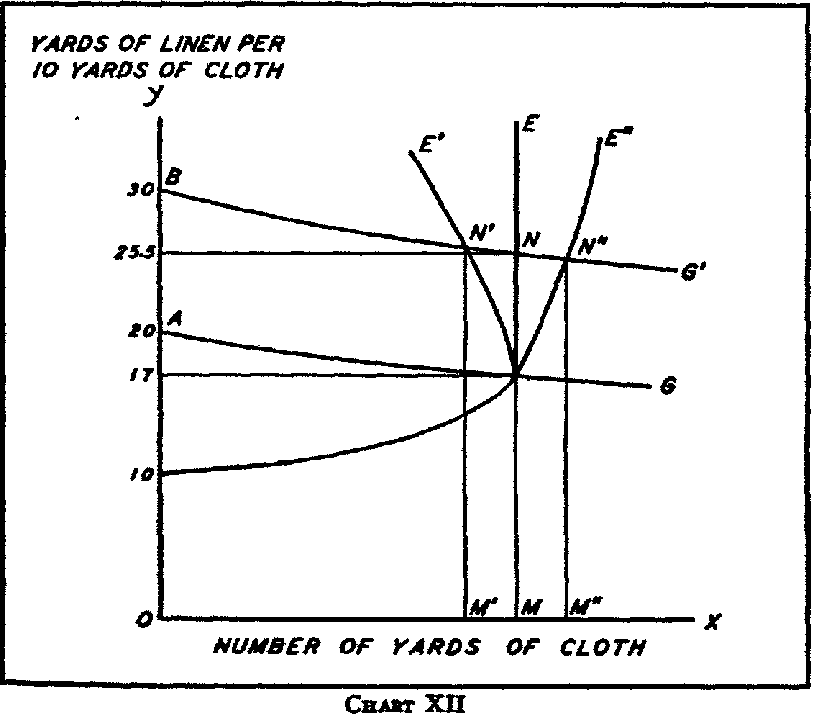
There are two countries, Germany and England, two commodities, cloth and linen, and production is tacitly assumed to be under conditions of constant real cost. In England 10 yards of cloth cost as much to produce as 15 yards of linen, while in Germany 10 yards of cloth cost as much to produce as 20 yards of linen. England will therefore be an importer of linen and an exporter of cloth, and the possible range of the terms at which cloth will be exchanged for linen is between 10 of cloth for 15 linen and 10 of cloth for 20 linen. Mill assumes that the reciprocal demands are such that equilibrium will be established at 10 of cloth for 17 linen.
Mill now assumes that an improvement is introduced in the method of production of linen in Germany, so that it now costs per unit only two-thirds as much as before. This will increase the German demand for cloth in terms of linen, and will cause 10 yards of cloth to exchange for more than 17 linen. Mill tacitly assumes here that the German demand for cloth
in terms of units of German effort of production will remain unchanged, so that the German demand for cloth
in terms of linen will at all points be 50 per cent higher than before. He concludes that the degree in which the amount of linen exchanging for 10 of cloth rises above 17 depends on the character of the English demand for linen in terms of cloth. When the German offering price of linen in terms of cloth is lowered: (a) if the quantity of linen England will take increases “in the same proportion with the cheapness” of the linen, i.e., if the English demand for linen in terms of cloth prices has unit elasticity, the new equilibrium terms of trade will be 10 cloth for 25½ linen; (b) if the quantity of linen England will take increases “in a greater proportion than the cheapness” of the linen, i.e., if the English demand for linen in terms of cloth prices has an elasticity greater than unity, the new equilibrium terms of trade will be 10 cloth for 25½—linen; (c) finally, if the quantity of linen England will take increases “in a less proportion than the cheapness” of the linen, i.e., if the English demand for linen in terms of cloth prices has an elasticity less than unity, the new equilibrium terms of trade will be 10 cloth for 25½ + linen.
Chart XII, a modification of the Marshallian foreign-trade diagrams so as to make the vertical axis represent the linen-cloth terms of trade instead of the total quantity of linen, shows that Mill’s conclusions, given his assumptions, are correct.
*21 The reduction in the cost of producing linen in Germany results in the terms of trade moving against linen. Given the effect of the reduction in the German cost of producing linen on the German demand for cloth in terms of linen, the degree of this movement of the terms of trade against linen is smaller, the greater is the elasticity of the English demand for linen in terms of cloth.
*22When the elasticity of the English demand for linen in terms of cloth (the
E curve) is unity, the new terms of trade are 10 cloth for 25½ linen. When the elasticity of the English demand for linen
in terms of cloth (the
E” curve) is greater than unity, the new terms of trade are 10 cloth for 25½—linen. When the elasticity of the English demand for linen in terms of cloth (the
E’ curve) is less than unity, the new terms of trade are 10 cloth for 25½ + linen. All these results are in conformity with Mill’s findings.
As the result of criticisms from W. T. Thornton, and others, Mill, in the third edition (1852) of his
Principles, introduced new matter intended to meet the objection that he had failed to demonstrate that, given the reciprocal demands, there was a unique rate of exchange between cloth and linen at which the condition of equilibrium that the value of imports should equal the value of exports would be met.
*23 There has been general agreement that this additional material was unsatisfactory and unnecessary. Where at least one of the reciprocal demands is inelastic there may be more than one equilibrium set of terms of trade, and the problem is then indeterminate.
*24 Where both the reciprocal demands are elastic, there must be a unique equilibrium set of terms of trade, which is adequately determined by Mill’s original procedure.
Marshall.
Marshall’s treatment of the relation of reciprocal demand to terms of trade is in the main an exposition and elaboration in geometrical form of Mill’s analysis.
*25 Marshall invented for this purpose a new type of supply-and-demand diagram, in which the vertical and the horizontal axes each represent the total quantity of one of the two commodities, thus differing from his domestic-trade diagrams, where only one commodity, and money prices, are involved, and where the vertical axis represents price per unit.
*26 As against the alternative procedure followed here in
charts VII, X, and XII, of making the vertical axis in the international-trade diagrams represent the terms of trade, equivalent to price, Marshall claims for his own procedure: first, that it makes the curves of the two countries “symmetrical” and, second, that the alternative procedure would have some (unspecified) advantages, but “this want of symmetry would have marred, though it would not have rendered impracticable, the application of the method of diagrams to the more elementary portions of the theory; but in other portions it would have led to unmanageable complications.”
*27
The issue is merely one of comparative convenience, and has no other significance. I have found it much more convenient as a rule to follow the procedure which Marshall rejects, i.e., to make the vertical axis represent terms of trade rather than the total quantity of one of the commodities. Aside from whatever aesthetic value may attach to the “symmetry” which is abandoned when this alternative procedure is followed, the only disadvantage in substituting the “terms-of-trade diagrams” for Marshall’s diagrams is that whereas in Marshall’s diagrams it can readily be determined by inspection, for
both of the curves, whether their demand elasticity is greater, less, or equal to unity, and for
both of the commodities, what will be the total amounts exchanged under equilibrium, in my diagrams, to which I will henceforth refer as “terms-of-trade diagrams,” this information is directly available only for one of the curves and one of the commodities. But my diagram has the advantage that on it the commodity terms of trade can be read off directly from the vertical axis, whereas on Marshall’s diagram they can be found only by determining the rate of slope of the vector from the
O point to the point of equilibrium.
The general nature of Marshall’s analysis of the relationship between the reciprocal demands and the terms of trade can conveniently be illustrated by means of one of Marshall’s propositions which Graham has criticized. That the use of terms-of-trade diagrams has some practical advantages over Marshall’s procedure will become evident, I believe, if the simplicity of the diagrams
presented here is compared with the complexity of those used by Marshall in the same connection. Marshall claims that if the English demand for German goods undergoes a given percentage increase the following rule holds:
The more elastic the demand of either country, the elasticity of the demand of the other being given, the larger will be the volume of her exports and of her imports; but the more also will her exports be enlarged relatively to her imports; or, in other words, the less favorable to her will be the terms of trade.
*28
Graham objects that the rule holds for Germany, but not for England, where “the more elastic the demand of E, the demand of G being given, the
smaller will be the volume of E’s imports and exports, and the less will her exports be enlarged relatively to her imports.”
*29 Marshall applies his conclusions only to curves of the “normal” type, i.e., curves whose “demand elasticities” in my terminology are greater than unity,
*30 while Graham makes no qualification whatsoever with respect to the nature of the curves. Since the results in some respects vary
in direction according to whether the elasticities are greater or less than unity, it will be assumed that Graham also intended to restrict his conclusions to cases where the elasticities are greater than unity. Since “increase” of demand can be given a variety of meanings, and the results obtained will depend on what meaning is chosen, I will assume, as does Marshall, that when a reciprocal demand “increases” it shifts
to the right by a uniform
percentage at all points of the original curve.
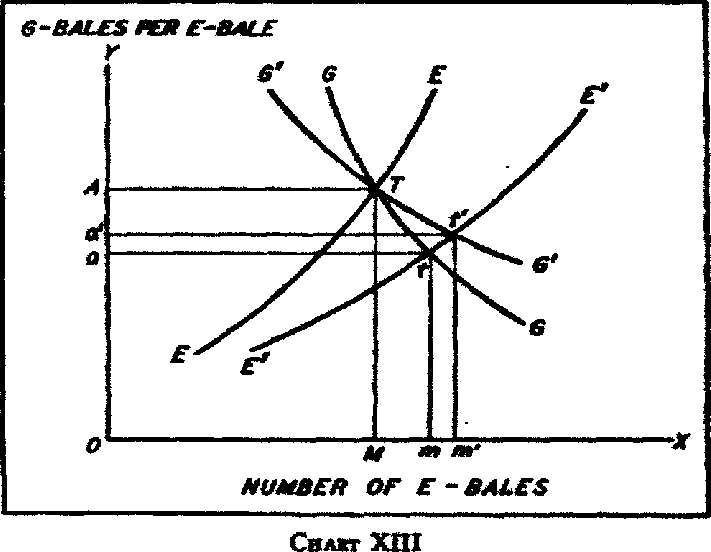
Marshall’s proposition is tested with reference to the influence of the elasticity of
Germany’s curve in chart XIII, where
EE is the original English supply curve (equivalent to Marshall’s original English curve), E’E’ is the increased English supply curve,
GG is the less elastic and G’G’ is the more elastic German demand curve. The more elastic the German demand curve: (1) the greater is the increase in the German exports (i.e., the rectangle
a’om’t’ >
aomt); (2) the greater is the increase in German imports (i.e.,
om’ >
om); and (3) the smaller is the amount of
movement favorable to Germany in the terms of trade (i.e.,
Aa’ <
Aa). These results are all in conformity with Marshall’s—and Graham’s—findings.
The divergent propositions of Marshall and Graham with respect to the influence of the elasticity of
England’s curve are tested in chart XIV, where
GG is the German reciprocal-demand curve,
EE and E’E’ represent the less elastic English reciprocal-demand curve before and after its increase, and
ee and
e’e’ represent the more elastic English reciprocal-demand curve before and after its increase. The more elastic the English reciprocal demand, then when the English demand increases: (1) the
smaller is the increase in the English exports (i.e.,
om <
om’); and (2), the
smaller is the movement of the terms of trade against England (i.e.,
Aa’<
Aa’). Both these results confirm Graham’s rather than Marshall’s findings.
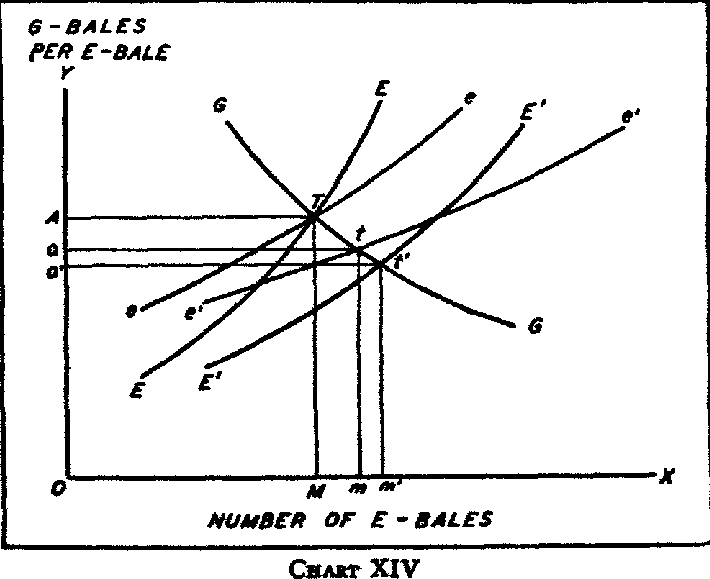
There remains to be considered Marshall’s finding that the greater the elasticity of the English curve the greater will be the increase in the English imports when the English reciprocal demand increases, and Graham’s contrary finding that the increase in the amount of English imports will be negatively correlated with the elasticity of the English curve. Marshall says, in effect,
that in chart XIV
aomt >
a’om’t’, while Graham contends that
aomt <
a’om’t’. Their conclusions, it is to be remembered, are here being checked only for the cases where all the curves have demand elasticities greater than unity. Since the less elastic the original English supply curve, the further to the right from
T along the
GG curve is the intersection of the increased English supply curve with the German curve (i.e.,
t’ is to the right of
t), and since, because
GG has an elasticity of demand greater than unity, the further from the zero vertical axis is the point of intersection of the increased English curve with the German curve the greater must be the size of the rectangle bounded by the perpendiculars dropped from that point to the zero axes, therefore,
a’om’t’ >
aomt. Graham, therefore, is here again right, and Marshall wrong. The unnecessary complexity of Marshall’s diagram seems to have concealed from him the fact that it provided no answers to the questions which he was putting, for the diagram by which he attempts to demonstrate the nature of the dependence of the results of an increase in the English reciprocal demand on the degree of elasticity of that curve shows three
original English curves, different in locus as well as elasticity, and fails to
present a comparison of the effects of an
increase in an original English curve according as that original curve has high or low elasticity.
*31
Edgeworth.
In Edgeworth’s treatment of the relation of reciprocal demand to the terms of trade the Marshallian graphical technique is still further elaborated, with conclusions similar in their general tenor, but with more detailed differentiation of the various possible types of cases.
*32 Of special interest is his diagram
*33 reproduced above (chart XV), intended to show the nature of the relationship between the comparative costs and the reciprocal demands.
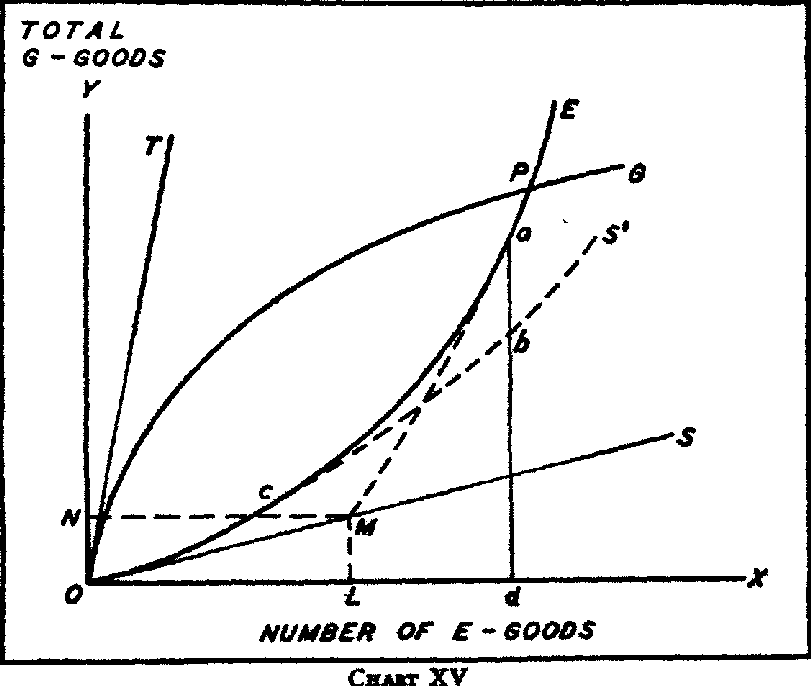
Chart XV is constructed on the Marshallian model, where the total amount of German linen is measured on the
Y axis and the
total amount of English cloth on the
X axis. The lines
OS and
OT are added, however, their slopes representing, on the assumption of constant costs of production, the (constant) ratio of the cost of production of a unit of linen to that of a unit of cloth, for England and Germany respectively. These lines therefore represent, respectively, the terms on which England could obtain linen and Germany could obtain cloth in the absence of foreign trade, and the equilibrium terms of trade must fall between these two lines. As Edgeworth draws the diagram, however, it is open to a criticism to which all the Marshallian diagrams as usually drawn are equally open, if they are supposed to represent two commodities or classes of commodities both of which are producible at home at constant costs (or at constant relative costs). In Edgeworth’s diagram the
OE curve begins immediately at its origin at
O to rise above the
OS line, and the
OG curve to fall below the
OT line.
*34 But the
OE curve will not diverge from the
OS line until the point on
OS is reached which corresponds by its vertical distance from the
X axis to the amount of linen which England would consume and produce in the absence of foreign trade. Let us suppose that the amount of linen which would be produced and consumed in England in the absence of foreign trade is equal to
ON. England would therefore be willing to export, at the limiting ratio of linen to cloth set by its home costs, any quantity of cloth not exceeding
NM, or
OL. The English export supply curve of cloth, in terms of linen, therefore, instead of being
OE, would be identical with
OS until the point
M was reached, and would diverge from
OS away from the
OX axis only beyond
M, the entire curve having somewhat the appearance of
OME. Similar reasoning applies to the relationship of the
OG curve to the
OT line.
*35
Graham.
Graham has criticized the reciprocal-demand aspects of the theory of international value as presented by J. S. Mill and Marshall as being fallacious in their essence.
*36 Some of his criticisms have already been examined.
*37 Still others, of greater consequence if valid, are here taken up for scrutiny.
Graham claims that where there are more than two commodities and more than two countries (all of them able to produce all or most of the commodities) fluctuations in the rate of interchange between the various commodities must be confined within a rather narrow range.
This is due to the fact that any alteration in the rate of interchange will affect the margin of comparative advantage of some country in the production of some one of the commodities concerned, will bring that country in as an exporter where formerly it was an importer, or as an importer where formerly it was an exporter, according as the terms of interchange move one way or the other, and, by the affected country’s addition to the supply or demand side, will keep the terms of interchange from moving far from their original position.
*38
Graham claims that Mill, Marshall, and their school grossly exaggerated the importance of reciprocal demands in determining the terms of trade and correspondingly minimized the importance of comparative-cost conditions in the determination of the terms of trade, and he attributes this error mainly to their assumptions of only two countries and of only two commodities, or of fixed physical compositions of each country’s exports and imports. He claims to demonstrate that “the character (urgency, elasticity, and the like) of reciprocal national demand schedules for foreign products is…of almost no importance in determining long-run ratios of interchange of products….”
*39
Graham here does point to a defect in the exposition of Mill and his followers, but he exaggerates its prevalence, misinterprets the exact nature of the defect, and errs himself in the opposite direction. In the exposition of Mill and his followers, the defect is not that they exaggerated the importance of reciprocal demand in the determination of the terms of trade, which is logically impossible, but that, whatever they may have known, they did not sufficiently emphasize the influence of cost conditions on reciprocal demand. The terms of trade can be directly influenced by the reciprocal demands
and by nothing else. The reciprocal demands in turn are ultimately determined by the cost conditions together with the basic utility functions.
*40
What Mill and his followers overemphasized was the importance
of the basic utility functions in determining the terms of trade. This defect in the exposition of Mill and his followers was undoubtedly promoted by the practice of confining the analysis to two countries and to two commodities, or to exports and imports of a fixed composition as far as the range of commodities was concerned, and to the assumption of constant costs, for under these conditions the cost conditions exhaust their influence in setting fixed maximum and minimum limits to the range of variation of the terms of trade.
Whatever may have been true of Mill, however, Marshall, Edgeworth, and other followers of Mill were aware of the fact that the greater the number of countries and the greater the number of commodities, the greater is the influence of cost conditions on the reciprocal demands and therefore on the terms of trade, and the smaller, therefore, given the cost conditions, the range of possible variation in the terms of trade as the result of given changes in the basic utility conditions. The first quotation following shows that Marshall appreciated the importance of multiplicity of commodities and of countries in causing the reciprocal demands to be elastic and therefore in restricting the range of variation of the terms of trade, and the second quotation, from Edgeworth, shows that Bastable and Edgeworth both recognized the similar effect of multiplication of countries.
It is practically certain that the demands of each of Ricardo’s two countries for the goods in general of the other would have considerable elasticity under modern industrial conditions, even if
E and
G were single countries whose sole trade was with one another. And if we take
E to be a large and rich commercial country, while
G stands for all foreign countries, this certainly becomes absolute. For
E is quite sure to export a great many things which some at least of the other countries could forego without much inconvenience: and which would be promptly refused if offered by her only on terms considerably less favourable to purchasers. And, on the other hand,
E is quite sure to have exports which can find increased sales in some countries, at least, if she offers them on more favorable terms to purchasers. Therefore the world’s demand for
E’s goods…is sure to rise largely if
E offers her goods generally on terms more advantageous to purchasers; and to shrink largely if
E endeavors to insist on terms more favorable to herself. And
E, on her part, is sure on the one hand to import many things from various parts of the world, which she can easily forego, if the terms on which they are sold are raised
against her; and on the other to be capable of turning to fairly good use many things which are offered to her from various parts of the world, if they were offered on terms rather more favorable to her than at present.
*41
The theory of comparative costs is not very prominent from the mathematical point of view….That the point of equilibrium [terms of trade] falls between the respective [trade] indifference-curves is the geometrical version of comparative costs. The expression which occurs in some of the best writers, that international value “depends on” comparative cost, is seen from this point of view to be a very loose expression. (No doubt, as Professor Bastable has pointed out, when there are numerous competing nations, the limits fixed by the principle of comparative cost are much narrowed and accordingly it becomes less incorrect to regard the principle as sufficient to determine international value).
*42
Graham’s own error lies in his failure to distinguish between the reciprocal demands and the basic internal utility functions and to see that the cost conditions can operate on the terms of trade only intermediately through their influence on the reciprocal demands. Graham fails, apparently, to see that in the elaborate arithmetical illustrations which he presents as demonstrations that the terms of trade are fixed within narrow limits by the cost conditions irrespective of the state of the reciprocal demands, there are present, explicitly or implicitly, rigorous utility and demand assumptions, and that, consequently, his illustrations really show that it is the ost conditions
plus the utility conditions which determine the reciprocal demands, and that it is only indirectly, through their influence on the reciprocal demands, that the cost conditions exercise any influence at all on the terms of trade.
*43
Even if the reciprocal demands were highly elastic, moreover, while substantial movements in the commodity terms of trade would thereby be rendered less probable, they would not, as Graham contends, become impossible.
*44 Let the original reciprocal-demand schedules be as elastic as one pleases, short of infinite elasticity, if they undergo pronounced shifts in position in opposite directions there will result a substantial change in the commodity terms of trade, as experiment with a Marshallian diagram will readily confirm.
Graham points out that in their explanation of the determination of the terms of trade by reciprocal demands the neo-classical writers from J. S. Mill to Edgeworth assume a fixed composition, as far as the list of commodities is concerned, of the exports and imports of each country. He claims, however, that commodities may shift from the export to the import status, or may cease to be exported or imported, and that the terms of trade determine (or are a factor in the determination of) the line of comparative advantage and, therefore, the composition of the export and import lists of any country.
It is, in consequence, impossible to determine international values on the premise of a fixed composition of export and import schedules of the several countries reciprocally concerned. In taking this premise the neo-classical writers are, in fact, implicitly assuming the very ratio of interchange of products which they are trying to discover, since the premise can be valid only on the supposition of
some definite ratio of interchange. This defect in logic not only completely vitiates the general theory of international values which they set up, but it
also renders useless for this, though not for another, purpose, the whole geometrical and algebraic supplement to the theory which reached its apogee, perhaps, in the work of Marshall.
*45
Graham rejects Marshall’s suggestion of a “representative bale” and Edgeworth’s suggestion of an “ideal” export or import commodity as solutions of the problem:
It must be obvious that reciprocal demand is for individual commodities and not for any such uniform aggregate of labor and capital as a unit of the consolidated commodities concerned may incorporate, and that to construct demand schedules for representative bales the physical composition of which is inevitably changing as we move along the schedules, with commodities even shifting from one demand schedule to its reciprocal, is not only to build imaginary bricks with imaginary clay but also to commit the worse fault of assuming a homogeneity in the bricks which, though a logical necessity for the construction of the demand schedules in question, is at the same time a logical impossibility.
*46
I understand Graham’s argument to be that the theory of international values, as presented, say, by Marshall, is completely vitiated by its use of reciprocal-demand and terms-of-trade concepts requiring for their logical validity a non-existent fixity in the physical composition of the exports and imports of each region, and that the remedy lies in carrying on the analysis in terms of reciprocal demands for and ratios of interchange between individual commodities.
In trying to express in terms of averages the changes in relative prices of groups of export and import commodities where the physical constituents of the groups change we encounter the insoluble problem of economic index numbers.
*47 Marshall and Edgeworth probably gave inadequate attention to this problem, though it is impossible to conceive of their not being aware of it. Their “representative bale” concepts are obviously but euphemisms for “averages,” although where constant costs are assumed
weighting of export commodities by relative prices does give an unambiguous and precise index of the terms of trade as a ratio between the quantities of productive services whose products have equal value.
*48 It is a far cry, however, from conceding that precise and unambiguous measurement of the changes in the aggregate terms of trade is impossible where, as is always the case, the physical constituents of the exports and the imports are undergoing relative changes to conceding that analysis resting upon averages computed in the usual or “standard” ways is thereby rendered worthless. If that were true, then economics would indeed be in a hopeless plight. Graham’s objection would then serve to condemn every economic concept involving a sum or an average, including his own concept of single “commodities,” as he would soon discover if he were to attempt to define a “commodity,” say wheat, so that it did not involve a medley of different things constantly undergoing relative changes in quantity, quality, and price. The use of such concepts, in spite of their admitted imperfections, can be defended only because superior alternatives are unavailable, and because their imperfections are believed—or hoped—not to involve a range of probable error in the results obtained by their use sufficiently great, or uncertain, to deprive these results of significance for the purpose on hand.
What Graham offers as an alternative for the use of imperfect “average” concepts, namely analysis in terms of pairs of single commodities, is not a satisfactory one. The significance of the results obtained when
expressed in terms of a pair of single commodities depends upon whether the commodities singled out are “representative” or not of broad classes of commodities, and the problem of finding proper criteria of “representativeness” is essentially but another manifestation of the “averaging” problem.
Analysis of the determination of the terms of trade cannot itself be carried on in terms of pairs of single commodities, except on the assumption that these are the only commodities entering into trade, or are “representative” of trade as a whole. “Reciprocal demand” is not only an aggregative concept, but it designates an economic force which operates as an indivisible entity. “Each transaction in international trade is an individual transaction,” but the terms on which it is conducted are set for it by the market
complex as a whole. The prices of any particular export commodity and any particular import commodity are functionally related to each other, react upon each other, not directly (except to an insignificant degree) but through their membership in the price and utility and cost systems of the trading world, taken as a whole. In the case of foreign trade, changes in the desires for or costs of particular commodities operate to change the ratios of interchange between these commodities and other commodities only indirectly through their influence on money flows and on aggregate demands and supplies of commodities in terms of money. The reciprocal-demand analysis is an attempt, imperfect but superior to available substitutes, to describe the aggregate or average results of such changes in desires or costs when they affect appreciably a wide range of commodities.
III. TERMS OF TRADE AND THE AMOUNT OF GAIN FROM TRADE
Terms of Trade as an Index of Gain from Trade.
From the beginning of the classical period, if not earlier, the trend of the commodity terms of trade has been accepted as an index of the direction of change of the amount of gain from trade, and it is therefore an old doctrine that a rise in export prices relative to import prices represents a “favorable” movement of the terms of trade. It has been recognized at times that the proposition is valid subject only to important qualifications, but systematic discussion of the qualifications which are necessary, or of the nature of the connection between the commodity terms of trade and the amount of gain from trade, seems to be almost totally lacking in the literature.
Ricardo had little to say of the terms of trade as related to the gain from trade, perhaps because the question then came up only in connection with the unwelcome arguments that by monetary expansion, or by protective duties, the commodity terms of trade of a country could be made more favorable. While Ricardo did not deny that, of itself, an increase in the amount of foreign goods obtained in return for a unit of native goods was a favorable development, he was careful to point out that whether or not it reflected a genuine improvement in the position of the country depended on how it came, or was brought, about. He
was, in general, skeptical of the possibility of bringing it about deliberately, through governmental action,
*49 but conceded, reluctantly, that the levy of import duties might have such a result, accompanied, however, by offsetting disadvantages:
We shall sell our goods at a high money price, and buy foreign ones at a low money price,—but it may well be doubted whether this advantage will not be purchased at many times its value, for to obtain it we must be content with a diminished production of home commodities; with a high price of labor, and a low rate of profits.
*50
Although J. S. Mill laid much greater emphasis than did Ricardo on the connection between the terms of trade and the amount of gain from trade, he also did not accept a favorable movement of the commodity terms of trade as necessarily indicating a favorable movement of the amount of gain from trade. Thus, while he conceded that the imposition of protective import duties operated to change in a favorable direction the terms on which the remaining imports were obtained, he claimed that this advantage was more than offset by the loss of the benefit which had previously accrued from the trade in the commodities now produced at home under tariff protection.
*51 Similarly, when he showed that a reduction in the real cost of production of Germany’s export products would operate to turn the terms of trade against Germany, he refrained from drawing the conclusion therefrom that the reduction in cost would be injurious to Germany even in the least favorable case where the commodity whose cost of production had been reduced was not consumed at all within Germany itself.
*52
As we shall see later, Marshall and Edgeworth both adopted changes in “consumer’s surplus,” or its supposed equivalent, as a better index of change in the amount of gain from foreign trade than the movement in the commodity terms of trade. Taussig pointed out specific circumstances under which the commodity terms of trade would be a misleading index of gain from trade.
*53 The general position of the major writers in this field
was, it seems, therefore, that an increase in the amount of imports obtained per unit of exports was presumptive evidence of an increase in the amount of gain from trade, but that the validity of the presumption was subject to the absence of countervailing factors. As examples of such countervailing factors, Marshall took account of increases in the cost of the export commodities and Taussig referred to a decrease in the desire for the import commodities. But systematic inquiry into the relationship between the commodity terms of trade and the amount of gain from trade is not, I believe, to be found in the literature.
Jevons criticized Mill’s use of the commodity terms of trade as a measure of the gain from trade on the ground that the total amount of gain from trade depended on total utility, whereas the commodity terms of trade were related to “final degree of utility”: “in estimating the benefit a consumer derives from a commodity it is the total utility which must be taken as the measure, not the final degree of utility on which the terms of exchange depend.”
*54 In utility terms, the total amount of gain from trade can be defined as the excess of the total utility accruing from the imports over the total sacrifice of utility involved in the surrender of the exports. If it be permitted to waive the difficulty of applying utility theory to a group of persons or a “country,” the commodity terms of trade will at any moment always equal the ratio of the marginal disutility of surrendering exports to the marginal utility of imports. Disturbances will change the terms of this ratio, but not the ratio itself. The marginal unit of trade, therefore, will never, under equilibrium conditions, yield any gain, and whether or not a “favorable” movement of the commodity terms of trade will represent an increase in net
*55 total utility will depend on what, if any, changes occur (1) in the
utility function for imports, (2) in the disutility function for exports, (3) in the volume of trade. Reasoning such as this was presumably the basis of Jevons’s comment. As will appear from the subsequent analysis, however, Jevons went further than this reasoning would justify, when he suggested that Mill’s argument that the gain from trade increased with the relative cheapening of imports as compared to exports was less likely to be true than its converse, on the ground that “he who pays a high price must either have a very great need of that which he buys, or very little of that which he pays for it,”
*56 a proposition whose plausibility derives from the very defect of analysis which he had charged against Mill, namely, disregard of the total utility aspects of the problem.
There follows an examination of the possibility of so modifying the concept of terms of trade as to make it less open to Jevons’s criticism that it rests on a confusion of final degree of utility with total utility, although this examination is for the most part only implicitly in terms of utility analysis.
Different Concepts of Terms of Trade.
We will write
e to represent the export commodities,
i to represent the import commodities,
P for the price index number,
o for the initial year, and
I for the given year. An index of the
commodity terms of trade can then be represented symbolically as
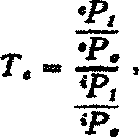
where the index measures the trend of the “physical” amount of foreign goods received in exchange for one “physical” unit of the export goods, with a
rise in the index indicating a
favorable trend, and vice versa.
*57
The case cited by J. S. Mill, where a reduction in the real cost to Germany of producing her export commodities would result
in a movement unfavorable to Germany of the commodity terms of trade but might nevertheless not involve a reduction in the amount of gain derived by her from her foreign trade, suffices to demonstrate that the commodity terms of trade may fail to provide a satisfactory guide even of the direction of the trend of gain from trade if, when the commodity terms of trade are changing, changes
in the same direction are occurring in the costs of production of the export commodities. If it were possible to construct an index of the cost of production in terms of the average technical coefficients of production of the export commodities, and if the commodity terms of trade index was multiplied by the reciprocal of the export commodity technical coefficients index, the resultant index would provide a better guide to the trend of gain from trade than the commodity terms of trade index by itself. This modified terms of trade index, which for lack of a better name I designate as the
single factoral terms of trade index, can be represented symbolically as:
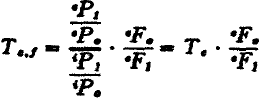
where
 represents the reciprocal of the index of cost in terms of quantity of factors of production used per unit of export, and
represents the reciprocal of the index of cost in terms of quantity of factors of production used per unit of export, and
Tc,f represents the index of the physical amounts of foreign goods obtained per unit of cost in terms of quantity of factors of production.
*58
A still closer approach to an index of real gain from trade would be achieved if the single factoral terms of trade index were multiplied by the reciprocal of an index of the “disutility coefficients” of the technical coefficients of the export commodities. The resultant index would be a
real cost terms of trade index, which could be represented symbolically as:
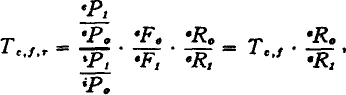
where
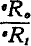 represents the index of amount of disutility (amount of irksomeness) per unit of the technical coefficients, and
represents the index of amount of disutility (amount of irksomeness) per unit of the technical coefficients, and
Tc,f,r represents the index of the physical amount of foreign goods obtained per unit of real cost.
The amount of gain from trade depends, however, not only on the amount of foreign goods obtained per unit of real cost involved in the production of the export commodities, but also on the relative desirability of the import commodities as compared to the commodities which could have been produced for home consumption with the productive resources now devoted to production for export. To take account of changes in the relative desirability of the import commodities whose internal consumption is precluded by the allocation of productive resources to production for export when such changes in relative desirability are due to changes in tastes, it would be necessary to incorporate in the “real cost of trade index” an index of the relative average
*59 utility per unit of imported commodities and of native commodities whose internal consumption is precluded by allocation of resources to production for export. If we write
U for average desirability or “utility” and
a to designate the commodities whose production for domestic consumption is forgone as the result of resort to production for export, then
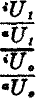 represents the index of relative desirability of import and forgone commodities, respectively, and the new terms of trade index, in which the index of relative desirability
represents the index of relative desirability of import and forgone commodities, respectively, and the new terms of trade index, in which the index of relative desirability
is incorporated, can be designated as the
utility terms of trade index, and represented symbolically as
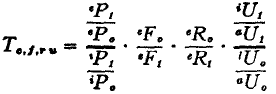 *60
*60Still another terms-of-trade concept was used by the older writers, namely, the number of units of the productive services of the foreign country whose product exchanged for the product of one unit of the productive services of your own country. This concept might be designated as the
double factoral terms of trade, and its index could be represented symbolically as
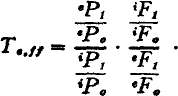
The older writers usually accepted the double factoral terms of trade as identical in their trend with the commodity terms of trade, which would be correct under their assumptions of production under conditions of constant costs and historically stable costs.
*61 But with costs variable, whether with respect to output or to time, the trends of the two indices could be substantially divergent. The double factoral terms of trade index would approach
more closely to an index of the international
division of gain than to an index of the absolute amount of gain for either country. If the commodity terms of trade and the index of export costs of a given country, A, remained the same, so that its single factoral terms of trade index remained unaltered, its double factoral terms of trade index would rise or fall according as the cost in the other country, B, of producing its exports rose or fell. But such divergence of the double factoral from the single factoral terms of trade index would have no welfare significance for country A, and, under the conditions stated, would merely indicate an impairment or improvement of productivity in country B.
Taussig has introduced still another concept of terms of trade, the
gross barter terms of trade, or the ratio of the physical quantity of imports to the physical quantity of exports, the greater this ratio the more favorable being the gross barter terms of trade.
*62 His purpose in introducing this concept is to correct the commodity, or “net barter,” terms of trade for unilateral transactions, or exports or imports which are surrendered without compensation or received without counterpayment, such as tributes and immigrants’ remittances. He gives an illustration where the price of wheat exported from the United States to Germany is 80 cents a bushel, and the price of linen imported into the United States from Germany is 76 2/3 cents a yard, so that the commodity terms of trade are 10 wheat for 10.4 linen. But of the 10,250,000 bushels wheat exported by the United States only 9,000,000 bushels are exchanged for German linen and the remaining 1,250,000 bushels are sent to Germany as the commodity equivalent of a compulsory tribute of $1,000,000. The United States thus surrenders 10,250,000 bushels wheat and receives 9,400,000 yards linen, with the ratio therefore, approximately 10 bushels wheat for 9.2 yards linen. This last ratio is Taussig’s gross barter terms of trade.
It is appropriate, perhaps, to make allowance in an index of gain from trade for unilateral transactions, or transactions without offsets on the other side, if such gains or losses can be properly attributed—which for most cases of unilateral transactions seems doubtful—to
foreign trade as their source or occasion.
*63 But to use the statistics of commodity exports and imports as the basis for calculating the gross barter terms of trade would in practice be liable to lead to seriously misleading results. Such procedure would lead to treatment as unilateral transactions of commodity exports or imports whose compensating import or export had taken place in the past—as in the case of exports whose cash proceeds are used to liquidate old indebtedness—or would take place in the future—as in the case of import surpluses constituting an import of borrowed capital—or took the form of an “invisible” import or export of services not recorded in the commodity trade statistics.
*64 It would seem, therefore, that, as Haberler suggests, allowance should be made separately for unilateral transactions, instead of incorporating them in the terms of trade index.
A further limitation of the terms of trade as an index of the amount of gain from trade, to which all the concepts of terms of trade differentiated above are subject, is that the terms of trade indices relate of a
unit of trade and therefore fail to reflect whatever relationship there may be between the
total gain from trade and the total volume of trade. But if whatever concept of terms of trade is used is accepted as a satisfactory index of the trend of gain from trade per unit of trade, multiplication of the terms of trade index by a physical index of the volume of trade will give an index of the total amount of gain from trade. For example, if we accept the commodity terms of trade as an index of amount of gain per unit of trade, and write
Q for volume of trade, our
index of total gain from trade would be
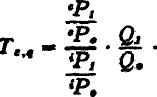
One advantage of a
total gain index over a
unit gain index
would be that it would clearly show that an increase in the total amount of gain from trade was consistent with an unfavorable movement in the index of unit gain from trade if the unfavorable change in the latter was associated with an increase in the volume of trade.
*65
Terms of Trade and the International Division of Gain from Trade.
J. S. Mill seems to have believed that the commodity terms of trade, taken in conjunction with its comparative costs, provided a criterion of the proportions in which the total gain from the trade of a particular country with the outside world was divided between that country and the rest of the world. He did not state clearly how he would determine the proportions in any particular case, given the actual terms of trade and the two limiting sets of cost ratios, but in one illustrative case, where costs of producing cloth and linen were in the ratio of 15:10 in England and of 20:10 in Germany, and where the actual terms of trade were 10 English cloth for 18 German linen, Mill says that “England will gain an advantage of 3 yards on every 15, Germany will save 2 out of every 20.”
*66 Cournot interprets this passage as postulating that England has a gain of 20 per cent and Germany a gain (or economy) of 10 per cent, although no percentages appear in Mill’s text. He points out, first, as ground for rejecting this mode of measuring the comparative gain from trade of two countries, that if one of the commodities could not be produced in England at any cost the English percentage of gain from trade would be infinite. He proceeds to a further criticism on mathematical grounds, which seems to me both unimportant of itself and irrelevant to Mill’s position unless it can be shown that Mill thought that England and Germany would, in his illustration, divide the gains from trade in the proportions of 20 and 10. Cournot says that it would be equally legitimate to hold that England as the result of trade gets 15 yards of linen for 8 1/3 yards of cloth instead of for 10 yards of cloth, a saving of 16 2/3 per cent, while Germany obtains, as the result of trade, 11 1/9 yards of cloth instead of 10 yards of cloth, for 20 yards of linen, a gain of 11 1/9 per cent. Measured this way, the ratio of the English to the German gain is 16 2/3:
11 1/3, instead of 20:10. “Or, les questions de calcul n’admettent pas de telles ambiguités. C’est qu’à vrai dire l’une et l’autre manière de compter sont purement arbitraires.”
*67
The real difficulty lies, however, in the inadequacy of the commodity terms of trade as a criterion of amount or division of gain from trade. The fact that, given the amount of gain, it will be expressed in different
percentages of gain according to what commodity is used as the base, seems to me to present a problem which is insoluble but of no consequence.
*68 It can be questioned also whether the proportions in which the total gains from trade are divided between two areas should be regarded as of much importance to either country, especially if the only procedures by which a country could divert to itself an increased proportion of the total gain should be such as would operate to reduce the absolute amount of gain it derives from trade—a not unlikely situation. If production is under conditions of varying costs, moreover, or if more than two commodities are involved, there will not be a single pair of comparative-cost ratios from which to compute the division of gain from trade. In the case of production under conditions of increasing cost, a situation is quite conceivable in which all the commodities which the respective countries import are also produced at home and in which, therefore, there are no comparative differences in
marginal costs under equilibrium, but where a substantial gain from trade nevertheless accrues from all the infra-marginal units of trade.
*69 In such a case, the method of computing the division of the gain from trade by comparison of the commodity terms of trade with the comparative marginal-cost ratios would be patently absurd.
Statistical Measurement of the Trend of the Terms of Trade.
Statistical attempts to measure the trend of terms of trade for actual countries and periods have been restricted to measurements of the commodity or of the gross barter terms of trade, and chiefly to measurements of the former. The problem of statistical measurements is obviously a less formidable one for these two concepts of terms of trade than for the more complex
and less objective ones examined above, but even if these simpler concepts are used the necessity of choice of index number formula to be used in computing the terms of trade index presents some difficult and in some respects insoluble problems.
The writers who have constructed statistical indices of the commodity terms of trade for particular countries and periods have made use of a wide variety of index number formulae, but have as a rule either offered no explanation of their particular choice of formula or have defended it on purely statistical grounds, such as simplicity, “reversibility,” or availability of data.
*70 Here, as elsewhere, it would appear that the choice of a formula should be made to depend on economic as well as on purely statistical considerations.
Let us suppose that an original static equilibrium in a particular country is disturbed by capital borrowings, that no changes occur except those resulting from the borrowings, and that the question asked is: What is the effect of the borrowings on the relative prices in the borrowing country of its export and its import commodities? Let us suppose also that the type of index number of export and of import prices which should be used in constructing the terms of trade index is a weighted aggregate index. Should the quantity weights to be used in comparing the terms of trade of a pre-borrowing with a borrowing year be those of the base, or pre-borrowing, year or those of the end, or borrowing, year?
*71
The proper answer depends on whether the question is asked as a question in the theory of the mechanism of international trade or as a question in the “theory of international values” or the theory of gain (and loss) from foreign trade. If the familiar proposition of the theory of the
mechanism of international trade that capital borrowings tend to raise export prices relative to import prices is to be tested statistically in terms of weighted index numbers, the weights used must be the quantities exported
and imported prior to the borrowings, since it is with the effect of borrowings on the relative prices of those commodities exported and imported before the borrowings that this proposition is concerned.
If what is to be tested, however, is the proposition that capital borrowings tend to improve the terms on which the borrowing country exchanges its exports for imports, the question of what type of weighting to use cannot be so readily answered. Gains to the borrowing country from the more favorable terms on which its exports are exchanged for imports can accrue only to the extent that such exchanges actually take place.
*72 In computing the export and import price indices for this purpose, should the prices therefore be weighted by the quantities exported or imported when the borrowings are under way, rather than by the pre-borrowing quantities?
In a closed economy, abstracting from sampling errors, the operation of the (ordinary Marshallian) elasticities of demand will tend to cause negative correlation between the relative changes in the
p’s and the relative changes in the
q’s, if the changes in the relative prices of particular commodities are due to changes in their relative costs of production, and to cause positive correlation if the changes in the relative prices are due to relative changes in demands for particular commodities. Similarly, in foreign trade, if the changes in the export prices of our country result from changes in the relative
world demands for its various export commodities, then the relative changes in the export
p’s and the relative changes in the export
q’s will tend to be positively correlated, whereas if the changes in the export prices are due to changes in the internal cost conditions, the relative changes in the
p’s and
q’s will tend to be negatively correlated. Similarly, the relative changes in the import
o’s and the import
q’s will tend to be positively correlated if they result from changes in the import demands for the various import commodities, and will tend to be negatively correlated if they result from changes in the foreign costs of production of these commodities.
But price indices based on end-year weights tend to have an upward bias as compared to price indices based on beginning-year weights if the changes in the
p’s and the changes in the
q’s are
positively correlated, and a downward bias if the changes in the
p’s and the changes in the
q’s are negatively correlated. In the choice of formulae to be used in constructing the price indices on which the terms of trade index as an index of gain is to be based, there is no obvious principle to follow in choosing between beginning-year and end-year weights, since neither procedure permits a wholly satisfactory comparison of the terms on which the actual exports and imports of the two years are exchanged. If the correlation between the changes in the
p’ and the changes in the
q’s has the same sign for both exports and imports, and if the same type of weighting is used for both price indices, the terms of trade index will tend to be unaffected by the choice made between weighting methods. But if the sign of the correlation between the changes in the
p’s and the changes in the
q’s is not the same for both exports and imports, or if different methods of weighting are used for the two price indices, the terms of trade index obtained for the end-year may differ substantially with differences in the choice of weighting-method.
There may be no rational basis for choice between beginning-year weight and end-year weights in constructing an index number of terms of trade where the problem consists of determining the effect of a particular disturbance on terms of trade in the “gain” sense. Comparison of the results obtained by the alternative methods of weighting in particular cases may be made, however, to serve as a check on the conclusions otherwise reached as to the nature of the disturbance. The type of correlation between the changes in the
p’s and the changes in the
q’s for the exports and the imports, respectively, and, therefore, the direction of the biases in the two price indices when based on end-year as compared to when based on beginning-year weights, should depend on the nature of the disturbance.
This reasoning can be illustrated by reference to the problem of the influence of capital borrowings on the terms of trade of the borrowing country. It has been argued above that capital borrowings tend to result in a rise in export prices and a fall in import prices in the borrowing country, not because of a relative shift in tastes whether in the world as a whole or within the borrowing country in favor of the export commodities of the borrowing country, but because of a relative rise in the money costs of production of the products of the borrowing country as
compared to the commodities it imports. If this reasoning is correct, we should expect to find the changes in the export
p’s and
q’s of the borrowing country to be negatively correlated, and its export-price index number for the end-year should be higher, therefore, if beginning-year weights are used than if end-year weights are used. If the export prices had risen primarily because of a rise in the world demand for the export commodities, the reverse results should be expected. Similarly, in the case of the import commodities, we should expect capital borrowings to result in negative correlation between the changes in the
p’s and the changes in the
q’s, and the import price index number, to be higher, therefore, for the end-year when beginning-year weights are used than when end-year weights are used; whereas if the changes in the import prices had resulted primarily from changes in the tastes of the population of the capital-borrowing country, the reverse result should be expected.
In my study of the Canadian experience under heavy capital borrowings, 1900 to 1913, I found that an export price index based on beginning-year weights rose to 135.6 in the end-year, as compared to 120.2 for an export-price index based on end-year weights, and that almost without exception the commodities whose exports constituted an increased proportion of the total Canadian export trade at the end as compared to the beginning of the period were commodities whose prices had risen by less than the average rise in export prices as a whole. These results are hard to explain for a small country, which would naturally tend to push most vigorously its exports of those commodities which had risen most in price, except on the theory that the rise in Canadian export prices relative to world price levels was the result primarily of a rise in Canadian production costs. I found confirmation of this theory in the fact that in general the commodities which did not clearly reveal the restrictive effect on Canadian exports of the general upward trend of money costs in Canada were commodities whose costs, because of conditions special to these commodities such as production from newly-discovered or newly-developed natural resources, escaped in part at least the general upward trend. Lack of necessary information prevented similar analysis of the import price trends for Canada. Studies by other writers of the effect of capital borrowings or other disturbances
on relative prices have not treated these problems
*73 and as a rule have dealt with cases where the disturbance was too small to be expected to have a clearly traceable effect on the price trends. The problem deserves further investigation, especially by the experts in index-number technique.
IV. “NET BENEFIT” IN INTERNATIONAL TRADE: MARSHALL
In what is in substance an attempt to find an objective counter-part for total utility analysis, Marshall applied to the problem of gain from trade a concept analogous to his concept of consumer’s surplus.
*74 Marshall here uses the terms “surplus” or “net benefit” instead of “consumer’s surplus,” perhaps because his procedure in his international trade analysis is supposed to account for “producer’s surplus” as well as for “consumer’s surplus.” In chart XVI,
*75OG is country G’s reciprocal-demand curve, and under equilibrium
OH units of G’s commodity are exchanged for
OB units of the commodity of the other country, E.
OR is the tangent to
OG at
O, intersecting
BA produced at
R. Through
P, any point on
OG, draw
OPp to cut
BR in
p; and produce
MP to
P1, so that,
M1 being the point at which it cuts
HA, M1P1 may be equal to
AP. Then G is willing to pay for the
OMth E-bale at the rate of
PM G-bales for
OM E-bales: i.e., at the rate of
pB G-bales for
OB E-bales. Country G therefore obtains a surplus on the
OMth bale at a rate which if applied to
OB bales would make an
aggregate surplus of
AP G-bales, or
M1P1 G-bales. Thus
her surplus on that
OMth E-bale is equal to
 . If
. If
P, starting from
O, is made to move along
OG, then
P1 will start from
U, the foot of the perpendicular drawn from
R on
OY; and it will trace out a curve
UP’A ending at
A. Then the aggregate surplus or net benefit which G derives from her trade will be an
OBth part of the aggregate of the lines
M1P1 as
P1 passes from
U to
A: that is, it will be an
OBth part of the area
UHA. Draw
VW parallel to
OX, so that the rectangle
VHAW is equal to the area
UHA. Then
 will be country G’s net benefit from trade, measured in G-bales.
will be country G’s net benefit from trade, measured in G-bales.
*76
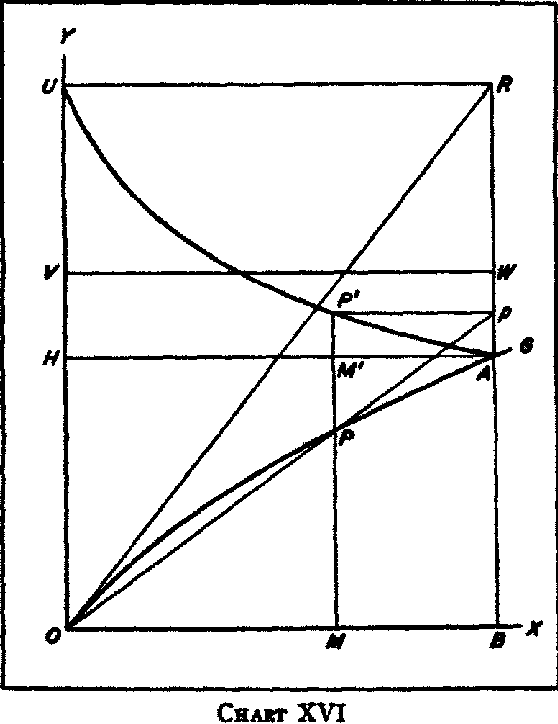
Marshall reaches these results by virtue of an interpretation of the reciprocal-demand curves which seems to me invalid. He
assumes that since country G would have been willing to take an
OMth E-bale at the rate of
Bp G-bales for
OB E-bales, but actually gets the
OMth bale—as all the other bales—at the rate of
AB G-bales for
OB E-bales,
Ap/
OB G-bales represents the surplus on the
OMth E-bale. But this assumes that country G would have been willing to take an
OMth E-bale at the
Bp/
OB terms even if she had already purchased (
OM-1) E-bales at terms less favorable than
Bp/
OB and it assumes similarly that country G would be willing to take an
OBth bale at the
AB/
OB terms if she had already purchased (
OB-1) E-bales at terms less favorable than
AB/
OB; i.e., it assumes that the rate at which earlier E-bales were actually obtained will not affect the rate at which country G would be willing to buy additional E-bales. The marginal utility to G of the G-bales she still retains will, however, be greater the greater the number of G-bales she has already surrendered, and, therefore, the amount country G would be willing to pay for an
OBth E-bale, when all the
OB bales are procured at the same price in G-bales,
AB/
OB, must be greater than the price she would be willing to pay for an
OBthe E-bale, when all the preceding (
OB-1) E-bales had been paid for at prices in G-bales higher than
AB/
OB. All of Marshall’s
M1P1‘s, therefore, except the initial one
UH, and consequently also the aggregate surplus for country G, are made by Marshall to appear greater than they would be if correctly computed. This exaggeration of the amount of surplus is inherent in Marshall’s method of computing it, which is capable of producing such improbable results as a surplus, measured in G-bales, many times greater than the total amount of G-bales actually exported, and—if the
OG curve is inelastic—may produce such meaningless results as a surplus, measured in G-bales, greater than the total amount of G-bales which G can produce.
Correctly to determine the consumer’s surplus measured in G-bales, it is necessary to go behind G’s reciprocal-demand curve to her utility functions with respect to the G- and the E-commodities.
Assuming this information to be available, we can proceed as in chart XVII, where the dotted lines and curves are a reproduction of chart XVI, included for comparative purposes only. By a procedure analogous to Marshall’s, we can draw the curve
OG1, such that at any point on it,
P1,P
1M/
OM or
p1B/
OB represents the number of G-bales which country G would be willing to give for an
OMth E-bale, when it had already bought (
OM-1) E-bales at the maximum prices in G-bales for each successive
E-bale which it would have been willing to pay, if necessary, given the prices at which the preceding purchases had been made. Except for the common point of origin,
O, the
OG1 curve would be lower at every point, with respect to the
OX axis, than the reciprocal-demand curve,
OG, at the corresponding points. On
MP1 mark off, from
M1,M1P11 =
Ap1, where
Ap1/
OB equals the excess
or deficiency in G-bales of what country G would be willing to pay for an
OMth E-bale if all the preceding E-bales had already been purchased at the maximum prices country G was willing to pay, over the price actually paid, or
AB/
OB. If
P1, starting from
O, is made to move along
OG1, then
P11 will start from
U and trace out a curve ending at
A1, the point at which the
OG1 curve cuts
BR. The aggregate surplus will then be
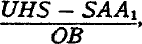 SAA1/
SAA1/
OB representing what the sum of the deficits on the purchases beyond the
S1 point would have amounted to if each unit of E-bales in turn were assumed to have been paid for at the
AB/
OB terms after each preceding E-bale had been paid for at the maximum price in G-bales which E would have been willing to pay, if necessary, given the prices at which the preceding purchases had been made. If
V1W1 is drawn so as to make the rectangle
V1HAW1 = the area
UHS–
SAA1, then the aggregate surplus of country G, measured in G-bales, will be
V1H, which is necessarily less than
VH.
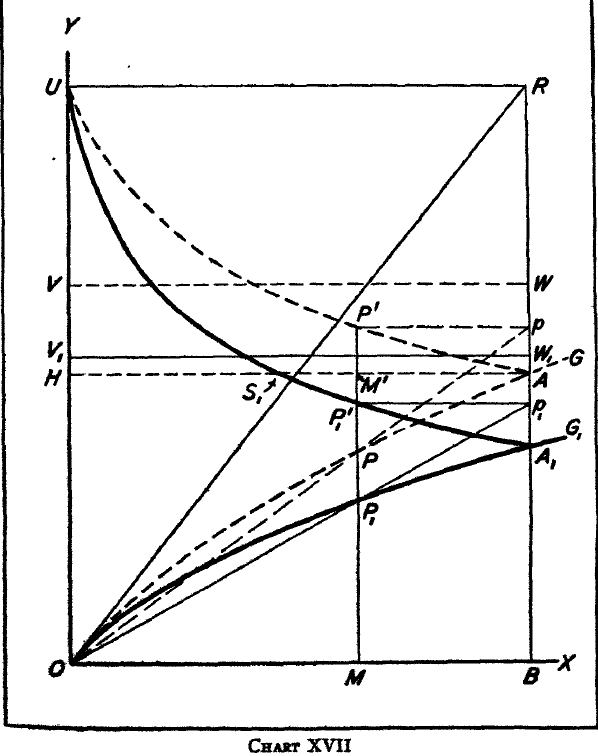
While the amount of surplus for country G will, therefore, necessarily be smaller than
VH in chart XVI, it will increase with any decrease in the price of E-bales in terms of G-bales, provided this decrease in price is not the result of a change in country G’s utility curves for G-goods or for E-goods—provided, that is, that it is not the result of a change in the
OG curve—and if the
OG1 curve is known it will be possible to determine the amount of change in surplus. Changes in
VH will normally be in the same direction, though not in the same degree, as changes in
V1H when the changes in the commodity terms of trade are not the result of
changes in
OG. For such changes, therefore, the effects on the surplus of country G, measured in G-bales, would be the same in direction, but would be smaller in degree, if determined by the method here presented than if determined by Marshall’s method. If Marshall’s “surplus” is accepted as a measure of gain, Marshall’s method will therefore produce results which for such changes are qualitatively right though quantitatively wrong.
Allyn Young,
*77 however, claimed that Marshall’s consumer’s surplus was a wholly unusable concept in international-trade theory: “consumer’s surplus, as Marshall measures it, is not additive. Its sum, for any one consumer, comes precisely to zero”;
*78 the objections against use of the concept are even stronger in the field of international trade theory than in the field of domestic trade theory.
*79
It is a familiar objection against Marshall’s concept of consumer’s surplus as used by him in domestic-trade theory, and an objection whose validity he conceded, that it is not “additive”; i.e., that the surpluses as computed by him for separate commodities cannot simultaneously exist. But in international-trade theory, Marshall posits only one surplus, that associated with the foreign trade
as a whole.*80 The surplus, moreover, is in international-trade theory measured in commodities having a direct utility of their own—or representing primary disutility—so that it cannot be said of G-bales, as it can of money, that their utility is merely a reflection of the utility of what can be obtained in exchange for them, and that the two utilities must therefore be equal.
*81
V. TOTAL NET UTILITY DERIVED FROM INTERNATIONAL TRADE: EDGEWORTH
Edgeworth’s analysis of the problem of gain from trade,
*82 the most elaborate and perhaps the least questioned in the literature, is both in method and in its conclusions in some important respects similar to, and in others different from, Marshall’s analysis. Edgeworth’s exposition is elliptical and cryptical, and is in part expressed in mathematical terms which I can follow only imperfectly. It is, therefore, with considerable trepidation that I present the following interpretation and criticism of his analysis.
Edgeworth uses reciprocal-demand curves of the Marshallian type to examine the direction of the effect on the amount of gain from foreign trade of disturbances of various kinds. He assumes tacitly that the curves in his diagrams represent the situation of typical individuals in the two areas, and bases his conclusions as to the direction of change in the amount of gain from trade on the proposition that movement from the point of origin of a given reciprocal-demand curve along the curve is always movement toward a position of greater total net utility (= consumer’s surplus) and therefore of greater advantage, a proposition which he had earlier demonstrated, given his assumptions, for domestictrade demand curves in terms of money,
*83 and which he here transfers to reciprocal-demand curves without further argument. Edgeworth does not here attempt to deal graphically with the
amount of change in gain from trade resulting from particular disturbances, but only with the
direction of the change in the amount of gain.
*84
The proposition that movement along a Marshallian reciprocal-demand curve from its point of origin tends on ordinarily reasonable assumptions to be movement towards a position of greater advantage can be accepted. But Edgeworth derives from it conclusions which differ substantially from those reached in the preceding two sections. These differences in conclusions can be summarized in the proposition that (with the exception of one special case, to be examined later) in Edgeworth’s results the direction of change in the amount of gain from trade and the direction of change in the commodity terms of trade always correspond,
*85 whereas it has here been argued that in many types of situations the commodity terms of trade and the amount of gain from trade may move in opposite directions was due to his failure, in his interpretation of his diagrams, to distinguish between disturbances involving movement along a
given reciprocal-demand curve and disturbances involving movement to a
new reciprocal-demand curve. One of Edgeworth’s diagrams, reproduced here as chart XVIII,
*86 is supposed to cover all cases where (1) the gain consequences for country E are alone being considered, (2) the disturbance originates in country E, and (3) the specific nature of the disturbance can be described as “H, where the change originates on the side of supply: such as increased facility of producing or exporting native commodities; [or] h, on the side of demand: such as an increased desire for, or facility in admitting foreign commodities.”
*87OE is E’s reciprocal-demand curve and
OG is G’s reciprocal-demand curve, and under the original equilibrium conditions
OM of E-goods is given by E in exchange for
ON of G-goods. A disturbance ensues, which is assumed to
be an impediment rather than an encouragement to trade, and to result in the
OE curve becoming “transformed” (the term is Edgeworth’s) to
OE’. Edgeworth traces the effects of the disturbance as follows:
In the new equilibrium indicated by the point
Q, RQ of
X is given in exchange for
QS of
Y. But
Q cannot be a position of greater advantage than
P’, where the horizontal through
Q cuts the original curve. For, on the most favorable supposition that the impediment affects only exportation, not production for internal consumption, (for instance, a transit duty imposed by a third country) England’s offer in exchange for
OR would be reduced by the impediment from
OS’ to
OS, so that
Q would be a position of just equal advantage as
P’. But
P’ is a position of less advantage than
P (being nearer the origin as you move along the curve). Thus the native country is prejudiced by the change.
*88
The mistake in this analysis is the identification, from the point of view of gain significance, of point
P’ with point
Q for all cases, including cases where there is no direct utility relationship between
the
OE and the
OE’ curves. In the case of a transit tax on country E’s exports, levied by a third country, where the horizontal distance between the
OE’ and the
OE curves represents the total amount of tax,
OE is still the real reciprocal-demand curve for country E, as seen by its inhabitants, while
OE’ is the same curve after the tax has been subtracted in E-bales, i.e., is E’s curve as seen by importers in country G. Under the new equilibrium, therefore, country E gives up
OS’ units of E-commodities in exchange for
OR units of G-commodities, while country G receives only
OS units of E-commodities in exchange for
OR units of its own commodities. The point
P’, therefore, represents the new equilibrium point on country E’s
unchanged reciprocal-demand curve, and because
P’ is nearer to
O than is
P as we move along the curve
OE, the new situation is less advantageous to country E than the old. The change in the gain from trade for country E corresponds in direction to the change in the commodity terms of trade for country E, since because
P’ is nearer to O along the
OE curve than is
P, and the
OE curve is concave upward with respect to
OX, the slope of the
OP’ vector with respect to
OX, which equals the new ratio in which G-commodities are obtained by country E in exchange for E-commodities, is smaller than the slope of the
OP vector, which equals the old ratio in which G-commodities were obtained by country E in exchange for E-commodities.
But let us suppose that the disturbance which results in the
OE curve being transformed to
OE’ consists of (1) a reduction in the desire of country E for G-commodities, or (2) an increase in the real cost of producing E-commodities, or (3) an increase in the desire of country E itself for E-commodities, all types of disturbances which Edgeworth believes to be covered by the diagram reproduced here as chart XVIII. The
OE curve, as the result of any one of these types of disturbances, now has nothing but historical significance, is a quondam curve of reciprocal-demand, and
OE’ becomes the real reciprocal-demand curve for country E. The utility significance of two points cannot be compared unless both points relate to the same set of utility and disutility functions, whereas, under any of the three assumptions listed above, the change from the
OE to the
OE’ reciprocal-demand curves is associated with a change in these basic utility functions. It is therefore no longer possible to determine from
the position of
Q with reference to
P whether or not the new equilibrium situation is more advantageous to country E than was the equilibrium situation prior to the disturbance, since these are points on different reciprocal-demand curves whose utility relationship to each other cannot be known without more information than the diagram affords.
Note, however, the different effect on the commodity terms of trade of an impediment to E’s trade which involves no change in E’s real reciprocal-demand curve as compared to one which does involve such a change. The original commodity terms of trade were
ON/
OM, they become
OR/
OS’ for country E in the case of the transit tax, but become
OR/
OS in the case of a disturbance involving a real change in E’s reciprocal-demand curve. But
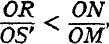 , whereas
, whereas
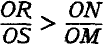 i.e., the commodity terms of trade change in different directions in the two cases. In the transit tax case, the change in commodity terms of trade and the change in the amount of gain from trade are necessarily in the same direction; in the other type of case the diagram does not afford sufficient information to determine what is the direction of the change in the amount of gain from trade.
i.e., the commodity terms of trade change in different directions in the two cases. In the transit tax case, the change in commodity terms of trade and the change in the amount of gain from trade are necessarily in the same direction; in the other type of case the diagram does not afford sufficient information to determine what is the direction of the change in the amount of gain from trade.
Except for one special case, still to be dealt with here, Edgeworth’s failure to discriminate in his interpretation of his diagrams between disturbances which result in the movement of the equilibrium point along the
given reciprocal-demand curve of the country under consideration and disturbances which result in that country acquiring a
new reciprocal-demand curve pervades his entire analysis, and suffices to account for the differences between the conclusions with reference to the relationship between changes in the commodity terms of trade and changes in the amount of gain from trade reached by him, and those presented above. That Edgeworth had noticed the correspondence between his results with respect to the direction of the changes in the amount of gain from trade and his results with respect to the direction of the changes in the terms of trade is indicated by the fact that when he criticized Mill’s procedure in accepting the trend
of the commodity terms of trade as a criterion of the trend of gain from trade, he added:
However, it may be admitted that his definition is adequate to the purposes for which it is used. Where he says that the whole or none, or more or less, of the advantage will accrue to a certain country, it is generally true, I think, not only in his sense, but in the more correct sense.
*89
In the special case to which reference was made above, Edgeworth does deal with a disturbance which causes a displacement of the equilibrium point off country E’s reciprocal-demand curve. But in this case, for special reasons, the original reciprocal-demand curve does not lose any of its utility significance, and Edgeworth provides the additional information necessary to make utility comparisons between the new equilibrium point and the original one. The diagram which Edgeworth uses to present this case is reproduced here as chart XIX.
*90 Country E levies a tax in kind on its exports, the proceeds, by exception, being distributed in such a manner as to offset any influence which the tax would otherwise have on the relative desires of the inhabitants of country
try E for the export and the import commodities.
*91OE and
OG are the reciprocal-demand curves of country E and country G, respectively, and the dotted curve is an indifference curve or locus of positions of trade which are of equal advantage to country E as position
P. We may call this dotted curve the trade-indifference curve. As Edgeworth says, this trade-indifference curve must touch the
OP vector at
P. If
Q, which by assumption is the new position of equilibrium on the curve
OG, is above
M, and inside the trade-indifference curve, the inhabitants of country E are benefited by the tax; if
Q is below
M they are prejudiced by the tax.
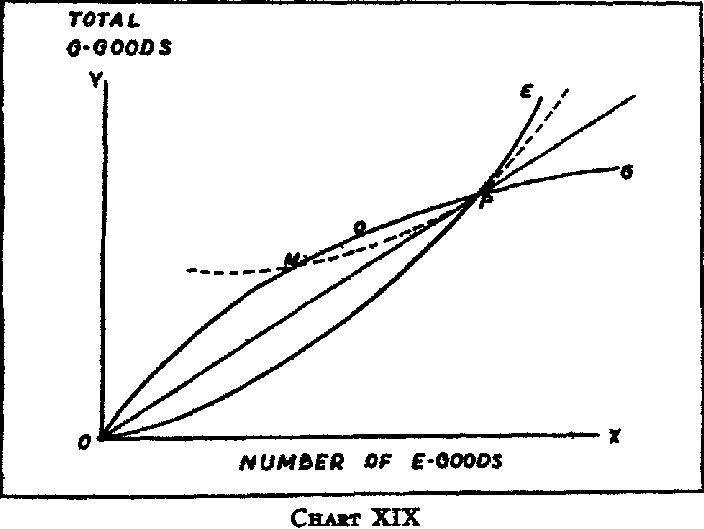
Edgeworth is able here to use the position of the new equilibrium point with reference to the trade-indifference curve as test of whether the new trading position is superior or inferior to the old for country E because
OE continues to be the reciprocal-demand curve of E as seen by its inhabitants—though not as seen by country G—and therefore the trade-indifference curve on which
P is located retains the same significance for the inhabitants of E after the tax as before. This special case, therefore, also fails to deal with a situation where a disturbance takes the form of a change in E’s basic utility functions, but while the commodity terms of trade necessarily move in favor of E, it is nevertheless possible for the new trade position to be less advantageous to E than the old one.
VI. THE GAIN FROM TRADE MEASURED IN MONEY
Marshall’s Curves and Monetary Curves.
In the theory of international value as expounded by Mill and his followers the analysis is conducted in terms of exchange ratios between certain broad groups or classes of commodities which together include all of the commodities existing in the two regions, or if the analysis is presented in terms of the exchange ratios between a few particular commodities, then these are assumed to be representative of the broad groups of commodities whose price interrelationships are the special subject of interest of the theory. In their general-value theory, on the other hand, the same writers dealt mainly with the prices in terms of money of single commodities taken one at a time and selected for examination from a universe in
which there was presumed to exist an indefinitely large number of kinds of commodities. In their handling of the theory of international value, therefore, the English school made two important change from their procedure in the field of general-value theory: (1) instead of dealing with money prices, they abstracted from money and dealt with exchange ratios between commodities; (2) instead of dealing with the variations in value of particular commodities taken one at a time on the assumption that the remainder of the system of values remained unchanged, they dealt with the internal variations occurring in the system of values as a whole. In their international-value theorizing, therefore, the English school, from the time of Mill on, made a substantial approach to the general-equilibrium method, although adhering, without important exceptions, to a strictly partial-equilibrium approach in the field of general-value theory.
This difference in method of analysis was not a historical accident but was a natural response to the difference in the nature of the problems which presented themselves most urgently for examination in the two fields. It is evident, however, that the earlier writers gave little thought to this divergence of procedure. Even in the case of Marshall, who is almost alone in drawing attention to the variation in his technique of analysis in the two fields, the explanation which he gives of the nature of the variation and of the considerations which make it desirable can scarcely be regarded as adequate. Marshall states that his reasons for dealing with international-value problems in non-monetary terms, as distinguished from the monetary approach of his general-value theory, are that any disturbance in international equilibrium will result in a change in the value of money in the two areas, or in “the standards of prices,” that if the analysis is in monetary terms allowance must be made for this change in value, but that attempt to make such allowance results in wholly unmanageable complications if one proceeds far into the pure theory of foreign trade.
*92
But the same objections,
in kind, can be made to the use of money prices as a measure of value in domestic-trade theory, and it is a difference in the nature of the questions examined in the two bodies of theory, involving a difference in the degree of error resulting from abstraction from the variations in the value of money, which provides any basis for tolerating this error in domestic-value theory in the interest of simplicity while refusing to tolerate it in the field of international values. The substitution for the price-quantity demand and supply functions for single commodities used in domestic-trade theory of some such concept as reciprocal demand becomes almost inevitable if what is being studied is the value relationships between all the elements of the economy, grouped into broad classes, instead of the relative variations in value of money and one single presumably minor commodity.
*93
It is a misconception, however, to regard the theory of international value, because it abstracts from absolute money prices, as a theory of barter applied to foreign trade. The theory of barter, strictly speaking, is not applicable to an economy in which money serves as a medium of exchange and as a common measure of relative values. The theory of international value takes for granted the existence of money and its execution of its respective functions, but confines its analysis to the non-monetary manifestations of the equilibrium process.
Marshall, who wrote during a period when the exponents of the substitution throughout the field of value theory of general-for partial-equilibrium analysis were carrying on vigorous propaganda for their cause, cannot be supposed to have been unaware of the full significance of his departure in the field of the theory of international value from the partial-equilibrium method which otherwise he uniformly followed. It is regrettable, therefore, that he not only failed to emphasize the differences between his methods
of analysis in the two fields, but that he expounded the two types of theory in such closely similar terminology as to lead some students to postulate a closer resemblance between the two bodies of analysis than could rightly be attributed to them. He must be held largely to blame, therefore, for the fact that able writers have supposed that his reciprocal-demand or foreign-trade curves and his domestic demand and supply curves in terms of money were so closely related that the former were simple derivatives of the latter.
*94 The two types of curves rest on radically different and irreconcilable sets of assumptions, so that it is impossible to derive one set from the other or to trace a definite relationship between them.
*95
The substitution in the theory of international values of analysis in terms of reciprocal demands for analysis in terms of demands and supplies of particular commodities with respect to money prices marks, therefore, a distinct improvement in method of analysis. For introducing this improvement the credit belongs mainly to John Stuart Mill, and when Marshall and Edgeworth later elaborated and refined upon it, and invented a graphical technique for its application, they freely acknowledged their indebtedness to Mill.
There exists, however, a considerable literature, mainly of Continental origin, and still being added to, in which the problems of international value are analyzed in terms of absolute money prices and of independence of particular demand or supply curves in terms of money prices from each other. Of the many variants of the monetary approach to the problem of international value there will be selected for comment here the three types which appear to have had the greatest influence on later writers.
Cournot’s Theory.
Cournot presents an argument for the profitability of import duties so obscurely stated and falling so far short of establishing its conclusions that it scarcely deserves attention on its own account. But his general authority as an economist is so high, and he is so often appealed to by protectionists as having successfully refuted the doctrine of comparative costs, that his argument cannot be wholly ignored. In spite of the fact that he stated his thesis at some length in all his economic works,
*96 it is by no means easy to determine just what he was trying to prove, and almost every commentator has given a different interpretation of his argument. I will attempt to reproduce his argument essentially in the form in which he first stated it.
*97
Country B removes a restriction on the import of a commodity M. Let
p
b be respectively the price and
D
b the consumption of M in B before the removal of restriction,
p’
b the (lower) price and
D’
b the (smaller) domestic production and
E the quantity
imported of M in B after the removal of the restriction. Then producers of M in B will lose

But for the consumers of M before the removal of the restriction there will be a saving of money available for the purchase of other commodities than M of

Since the import
E must be paid for in other commodities, a foreign sum is added to the funds previously available for the purchase of other commodities than M, equal to

On the other hand, the increase in the purchases of M resulting from the decrease in the price of M will reduce the amount otherwise available for the purchase of other commodities than M by the amount of

But (2)+(3)-(4), or the additional funds available for the purchase of other commodities than M, equals (1) or
pbD
b—
p’bD’
b, i.e., equals the loss to producers of M in B. It would seem that so far there is no net change in the national money income, since the loss to producers of M in offset by a corresponding gain to the rest of the community. But Cournot, by virtue of a process of reasoning which no one has so far satisfactorily explained, calls this sum,
pbD
b—
p’bD’
b, the “nominal reduction” in the national income.
*98
Cournot concedes that the original consumers of M, as a result of its fall in price, are in the same position as if their income had increased by

what we would call a consumer’s surplus item if this were an acceptable way of measuring it. There is also a possible additional gain to consumers of M, because at its reduced price the additional purchases thereof may yield more satisfaction than the commodities which they replace. But since Cournot regards this gain as not measurable, he excludes it from his computation. He concludes that there is a “real reduction” in the national income of B equal to the excess of the “nominal reduction” (1) over the gain (5), or
It is impossible to find any significance either in Cournot’s mode of computation of the benefits and losses from the removal of a restriction on import, or in the “nominal” or “real” results of his computations. The correctness of the general verdict that the technique which he used at this point was inadequate for the purpose and his conclusions of no value seems indisputable.
*99
In his final exposition of his thesis, Cournot concedes that if the removal of the restriction on import resulted in an outflow of money followed by a general fall in the prices of commodities, the problem would completely alter in character, and his conclusions
would not apply. This is an important concession, since the classical economists would have argued that a unilateral reduction in duties would have just these effects, and would have regarded as meaningless analysis of the effects of a reduction of duties which did not take these effects into account. Cournot also defends his technique of analysis in terms of money values by appealing to Mill’s doctrine that the introduction of money would not alter the results of trade as compared to what they would be under barter. If this was correct, Cournot asserts, there could be no objection to the presentation of the theory of international trade in wholly pecuniary terms.
*100 This is, of course, an extraordinary
non sequitur. Because analysis in terms of real costs, on the one hand, and analysis in terms of real costs
and money values, on the other hand, would produce identical results, it does not follow that the same results can be produced by analysis in terms of money values alone. In any case, Cournot’s analysis fails to deal intelligibly even with the pecuniary aspects of the problem.
Barone’s Graphical Technique.
Cunynghame, in 1904, expounded the theory of international value with the aid of a type of graphical illustration related to the ordinary Marshallian domestic-trade demand and supply diagrams in terms of money prices and derivable from them.
*101 In Cunynghame’s diagrams, as in Marshall’s domestic-trade diagrams, only one commodity at a time is under consideration, and the diagrams relating to the two regions are set back to back for purposes of comparison and analysis. Cunynghame did not draw any conclusions with respect to gain from trade from his diagrams, but Barone, in 1908, used the Cunynghame back-to-back diagram to reach such conclusions.
*102
Chart XX is a reproduction of Barone’s basic diagram.
*103 The demand and supply curves of the particular commodity under consideration, expressed in terms of money in a currency common to both countries, are given separately for each country, with the
two diagrams set back to back. In the absence of international trade in this commodity, its price would be
P
1N in England and
PM in Germany. If trade is opened, England will therefore be the importer of the commodity and Germany the exporter. The cost of transportation per unit is assumed to be
OO
1, and after trade, therefore, the price in England must be the price in Germany plus
OO
1. Equilibrium will be established at the price, f.o.b. Germany, at which the quantity England would import,
CT,*104 is equal to the quantity Germany would export,
EF.*105 The price, therefore, will be
RE in Germany and
HC (-
RE+
OO
1) in England. Each country, says Barone, will gain as the result of the trade. In England the gain to consumers will be
P
1CAB monetary units, which is greater than the loss to producers,
P
1TAB. In Germany the gain to producers will be
AZPF, which is greater than the loss to consumers,
AZPE.
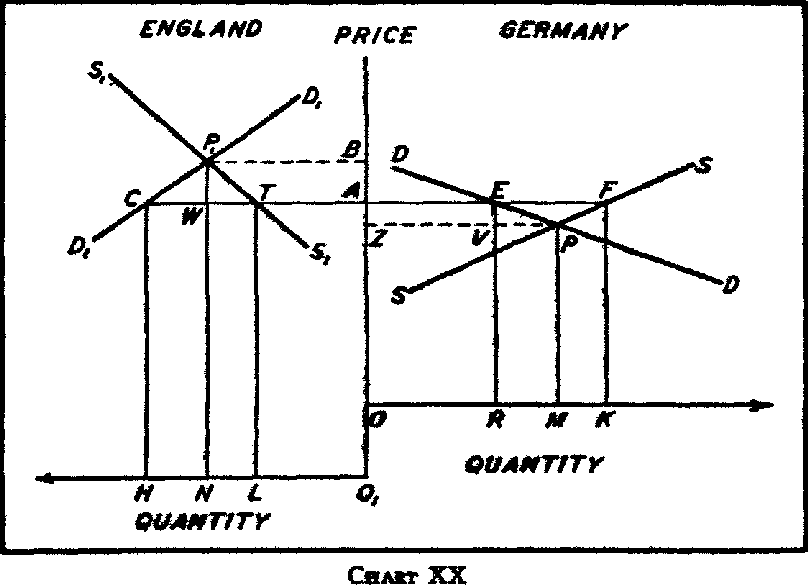
The grounds on which this reasoning must be regarded as inconclusive are many and formidable. First, it ignores the effect
which the removal of barriers to trade would have on gold movements and therefore on the heights of the demand-and-supply schedules and the prices in the two countries. Second, the area
CP1W included by Barone in the gain to English consumers is not homogeneous with the area
BP1WA, the latter being an actual saving in money (waiving the first objection), whereas the former is a “consumer’s surplus” of indefinable meaning as compared to the area
BP1WA. A similar objection applies to the inclusion of the area
EVP in the loss accruing to German consumers. These areas are akin to a portion of Marshall’s consumer’s surpluses in his domestic-trade theory, and are subject to the same criticisms. Third, the calculation of gain or loss to producers from changes in price and output assumes that the “producer’s rent” areas represent net real income to producers without involving real costs to anyone else in the community, an assumption inconsistent with normal reality in the one respect or in the other, or partly in both. Fourth, the supply and demand curves in terms of money for each country are assumed to be independent of each other, and of the amount of national real income, an assumption always logically invalid, but seriously in conflict with the realities if the commodity under consideration represents, or is taken as representative of, a large fraction of the total national output or consumption, as distinguished from the theory of domestic value. Barone’s technique of analysis is invalid, therefore, even if what is in issue is the gain or loss resulting from the removal of a single minor import duty, although the results which he obtains are for most situations probably the same
in direction as those which would be obtainable by more acceptable methods. But Barone claimed that his conclusions are “manifestly” applicable, without need of additional qualification, to the case of the removal of an entire tariff.
*106
Auspitz and Lieben.
Auspitz and Lieben attempt to trace the gain or loss effects of trade and of the imposition or removal of single duties by means of graphical constructions, independently devised by them, which are in some respects intermediate between the Marshallian domestic-trade diagrams and the Marshall-Edgeworth foreign-trade diagrams.
*107 In their diagrams only a single commodity and money are represented, as in the Marshallian domestic-trade diagrams, but the vertical axis represents total amount of money instead of price per unit, and for each country the demand or supply situation is represented by two curves. In the case of the exporting country, one of these curves represents the total amounts of money in return for which the country would carry its export to the volumes indicated by the horizontal axis, while the other represents the total amounts of money which the country could accept for the indicated volumes of export without losing from the trade as a whole. This last curve, therefore, is a species of indifference curve corresponding to one of Edgeworth’s “no-gain from trade” curves. It is assumed throughout that the money has constant marginal utility, and the effects of trade, or of duties, on the amount of gain from trade are measured by the vertical distances between the two curves. The restriction to single commodities makes the Auspitz and Lieben constructions akin to Barone’s as far as the objective effects of trade and of duties are concerned, and open to the same
objections, but their method of measuring gain, while not satisfactory because of the assumption of constant marginal utility of one of the constituent items in the trade, is superior to Marshall’s because of its use of the indifference curve as an element in the measurement.
This book may appropriately end on a not which has been repeatedly struck before. The theory of international trade, at its best, can provide only presumptions, not demonstrations, as to the benefit or injury to be expected from a particular disturbance in foreign trade, for it deliberately abstracts from some of the considerations which can rationally be taken into account in the appraisal of policy and it never takes into account all the variables which it recognizes as significant and within its scope either because they are out of its reach or because to take them all into account would make the problem too complex for neat solution. The presumptions which the theory does provide, however, are important both because neglect of them in the formation of decisions as to policy would lead to wrong decisions in many, perhaps most, cases, and because these presumptions are not likely to be hit upon except by means of the rather arduous procedures of the theory of international trade in its more or less traditional form. Greater claims than this have been made for the utility of theory in the field of commercial policy, but their justification must await, I fear, an advance in power of economic analysis which is not yet in sight.
economies. The economies of international trade are by no means an exact measure of its net benefits. But that net benefits are more or less according as the economies secured are more or less, is a justifiable assumption.”—”Marshall on consumer’s surplus in international trade,”
Quarterly journal of economics, XXXIX (1924), 150. (Italics in the original.)
Principles of political economy, 1st ed., 1820, pp. 461-62. (Italics in the original text.)
ibid., p. 460.
Principles of political economy, 1st ed., 1817, p. 107.
Principles, Works, 260: “One set of necessaries and conveniences admits of no comparison with another set; value in use cannot be measured by any known standard; it is differently estimated by different persons.”
(Some leading principles of political economy, 1874, p. 421.)
Essays on some unsettled questions of political economy, written in 1829-30, when he was twenty-three years of age, but not published until 1844. He reproduced it, with extensions, but also with important omissions, in the first edition (1848) of his
Principles of political economy, bk. iii, chap. xviii, “Of international values.” Edgeworth could not find terms of praise too high for this chapter; it was a “great chapter”
(Papers relating to political economy, 1925, II, 7), a “stupendous chapter”
(ibid., II, 10, 20), and an exposition of the general theory which was “still unsurpassed”
(ibid., II, 20). Graham, on the other hand, declares that it presents doctrine which is “in its essence fallacious and should be discarded.”—”The theory of international values,”
Quarterly journal of economics, XLVI (1932), 581.
supra, pp. 453-54.
Principles, Ashley ed., p. 592:
The law…may be appropriately named the equation of international demand. It may be concisely stated as follows. The produce of a country exchanges for the produce of other countries at such values as are required in order that the whole of her exports may exactly pay for the whole of her imports. This law of international values is but an extension of the more general law of value, which we called the equation of supply and demand.
A system of political economy, 1877, p. 406.
Quarterly journal of economics, XLVI (1932), 606.
Theory of international trade, 4th ed., 1903, p. 180.
The letters of John Stuart Mill, H. S. R. Elliot ed., 1910, II, 207. (Italics in the original text.) Mill’s reasoning here is clear enough, and sound enough, if it is remembered that, like all the earlier English economists, Mill distinguished in his thinking, even if not in his terminology, between “demand” as a quantity actually taken at a particular price and “demand” as a schedule of quantities which would be taken at different prices.
Journal of the Royal Statistical Society, LII (1889), 557, fig. 3, for a similar demonstration by means of a Marshallian diagram.
X for the total amount of E-goods,
Y for the total amount of G-goods, the subscripts
E and
G for the countries England and Germany respectively,
y =
Y/
X for the price of E-goods in G-goods, and 1/
y =
X/
Y for the price of G-goods in E-goods. Then if
eDE is the elasticity of English “demand” or willingness to buy German goods,
eSE is the elasticity of English willingness to sell English goods,
eDG is the elasticity of German willingness to buy English goods, and
eSG is the elasticity of German willingness to sell German goods, then:
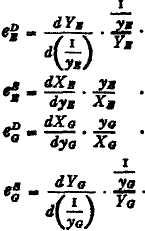
The demand elasticity and the supply elasticity of each country are of course closely related to each other, as they are but different aspects of the same phenomenon. The relationship between the two elasticities for England can readily be shown:

Similarly,
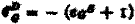
When the coefficient of demand elasticity of a country is unity, therefore, thecoefficient of its supply elasticity is zero. In the text, reciprocal-demand curves are referred to as “elastic” if the coefficient of their demand elasticity is numerically greater than unity and of their supply elasticity is algebraically greater than zero and as “inelastic” if the coefficient of their demand elasticity is numerically smaller than unity and of their supply elasticity is algebraically smaller than zero.
Although expressed in different terms, this usage corresponds to Marshall’s use of the terms “elastic” and “inelastic” in connection with his reciprocal demand curves. (Cf. Marshall,
Money credit & commerce, pp. 337-38, note.)
Principles, Ashley ed., pp. 596-604.
Money credit & commerce, p. 354, note 3.
(Memorials of Alfred Marshall, A. C. Pigon ed., 1925, p. 451.)
The pure theory of foreign trade (printed for private circulation in 1879, reprinted in 1930), and his
Money credit & commerce (published in 1923, though in the main written much earlier), bk. III, and appendices H and J.
Money credit & commerce, p. 178.
Quarterly journal of economics, XLVI (1932), 601.
supra, p. 539, note II, and Marshall,
loc. cit., p. 342.
Money credit & commerce, p. 343, fig. 12.
Papers relating to political economy, 1925, II, 31-40 (first published in
Economic journal, 1894, in substantially the same form).
supra, chart X, p. 468, for a terms-of-trade diagram drawn with reference to these considerations.
Edgeworth states that if production is not under conditions of constant cost, “there should be substituted for the straight line
OS (and
mutatis mutandis for
OT) a curve of constant advantage, or indifference-curve (not shown in the figure) representing states for which the advantage to England is no greater than if there had been no trade.” (
Papers, II, 33.) He must mean a curve representing states for which the importation of an additional unit of the G-good by country E would be no more advantageous than its production at home, if this curve is to be the analogue for variable costs of his
OS line. In chart XV,
OS is
not a “no-gain from trade” curve, but is a curve of “no-gain from import as compared to domestic production of the G-good.” If country E were to export more than
OL units of E-goods at the
ML/
OL terms—or even on terms more favorable to itself—it might be incurring a loss from undue specialization of the sort discussed in the preceding chapter. (See
supra, p. 451.) The location in the chart of a “no-gain from trade” curve requires knowledge of the utility functions as well as of the cost conditions. It would never fall below the
OS line (or, in the case of variable costs, the
OS’ curve) and would never rise as high as the
OE curve. (See
infra, p. 572.) I have inserted in chart XV a “no-gain from import as compared to domestic production of the G-good” curve,
OS’, applicable to conditions of increasing costs. At any point,
b, on
OS’, the slope with respect to
OX of a tangent to
OS’ at that point represents the number of units of G-goods which could be produced at home by country E at a cost equal to the cost of producing a unit of E-goods in addition to what would be its output of E-goods if it was exporting
Od E-goods in exchange for
db G-goods. (The slope with respect to
OX of the tangent to
OE at
a represents the number of units of G-goods per unit of E-goods in which country E would be willing to export
Od units of E-goods.) Since production is under conditions of increasing cost, the number of units of the G-good which country E could produce at the same cost as an additional unit of the E-good will be greater, the greater its output of E-goods. As
OS’ is drawn concave upward in chart XV, it is implicitly assumed that increased export of E-goods involves increased output of E-goods, i.e., that as more E-goods are exported, the domestic consumption of E-goods decreases, if at all, by a smaller amount than the increase in exports. The
OS’ curve must be drawn below the
OE curve at all points, and the identity of the two curves from
O to
C in chart XV is an error. Since in country E, for each output of E-goods corresponding to a given export by it of E-goods, its relative marginal costs of production of E-goods and G-goods must correspond to its supply-price of E-goods in terms of G-goods, a tangent to the
OS’ curve at any point must be parallel to a vector drawn from
O to the vertically corresponding point on the
OE curve. This excludes the possibility of identity of the two curves for any part of their course.
Quarterly journal of economics, XXXVIII (1923), and “The theory of international values,”
ibid., XLVI (1932).
loc. cit., p. 86.
loc. cit., pp. 583-84.
(The theory of international trade, 1936, p. 123.)
Money credit & commerce, p. 171.
Papers, II, 33. The sentence placed in parentheses appears in the original as a footnote.
loc. cit., p. 76) and the accompanying text, where it is assumed “that before international trade is opened up, each country devotes one third of its resources to each of the three products, and that each increases its consumption of the three products proportionately as it secures gains from international trade” (p. 70) even though important changes in relative prices are assumed to take place. With the additional information given as to the economic size of the countries, their cost conditions, and the prices within each country before trade, Graham is justified in his claim that the data given suffice to determine within narrow limits the equilibrium terms of trade when foreign trade is opened up. But he fails to substantiate his claim that it is the cost conditions alone which determine the terms of trade. If the cost conditions are left unchanged but his utility assumptions altered, the equilibrium terms of trade can be changed, within broad limits, in whatever degree and direction is desired.
The same criticism applies to the interpretation given by C. F. Whittlesey—”Foreign investment and the terms of trade,”
Quarterly journal of economics, XLVI (1932), 449, 459—of results similar to Graham’s obtained from arithmetical illustrations involving similar assumptions.
Whereas Graham criticizes the writers in the classical tradition for minimizing the influence of comparative costs on the terms of trade, Angell criticizes them for their alleged belief that comparative costs ”
in themselves alone, provide a sufficient a
prior explanation of the course and terms of trade.” (Angell,
Theory of international prices, 1926, pp. 371-73.)
loc. cit., p. 604: “If both demand schedules were elastic, movements in the terms of trade must necessarily be small.”
loc. cit., pp. 582-83. (Italics are in the original.)
Essays in applied economics, 1930, p. 150:
The value of imports in general in terms of exports in general is a notion of exactly the same sort as the value of things in general in terms of money. No precise significance can be given to this notion, and no completely satisfactory measure of changes in it can be devised.
infra, p. 561.
Notes on Malthus, pp. 70 ff.
supra, pp. 537 ff.
International trade, 1927, pp. 117-18.
The theory of political economy, 1871, p. 136. Cf. Edgeworth,
Papers, II, 22: “It is a more serious complaint that Mill takes as the measure of the advantage which a country derives from trade, the increase in the rate of exchange of its exports against its imports. He thus confounds ‘final’ with ‘integral’ utility; ignoring the principle of ‘consumer’s rent.'” Cf. also
ibid., “On the application of mathematics to political economy,”
Journal of the Royal Statistical Society, LII (1889), 558: “To measure the variations in the advantage accruing from trade by the variations of price—or more generally rate of exchange—is a confusion which could hardly have occurred to the mathematical economist.”
op. cit., p. 138.
unfavorable movement of the terms of trade. No question of principle is involved, but it seems to me to be more convenient to represent favorable movements of the indices by rising indices. The formulae which follow are so constructed that a movement of any element in the formula favorable to the country in question operates to raise the index, and vice versa.
home production of the import commodities, the single factoral terms of trade would send to exaggerate the trend of gain
from trade by treating as a gain from trade a gain from improvement in productivity which was not dependent upon foreign trade for its realization.
total utility of foreign trade, and the terms of trade index is brought closer to a total utility index if provision is made in it for changes in
average relative desirability.
Three lectures on the value of money, 1840, p. 66: “the demand in Europe and Asia for thé produce of Mexican labor having increased, the results of a given quantity of Mexican labor would command in exchange the results of a larger quantity of European and Asiatic labor than before.” Cf. also R. Torrens,
The budget, 1841-44, p. 28: “Where any particular country imposes import duties upon the productions of other countries, while those other countries continue to receive her products duty free, then such particular country draws to herself a larger proportion of the precious metals, maintains a higher range of general prices than her neighbors, and obtains, in exchange for the produce of a given quantity of her labor, the produce of a greater quantity of foreign labor.”
International trade, pp. 113-14.
ibid., pp. 119, 254. Cf. also Viner, “Die Theorie des auswärtigen Handel” in
Die Wirtschaftstheorie der Gegenuart, II (1928), 121ff.; White,
The French international accounts, 1933. pp. 238-41; Haberler,
Theory of international trade, 1936, pp. 161 ff.
International economics, 1933, pp. 32 ff., where this point is emphasized.
Revue sommaire des doctrines économiques, 1877, pp. 210 ff.
(Papers relating to political economy, 1925, II, 22, note) and Bastable
(Theory of international trade, 4th ed., 1903, p. 44, note) on Cournot’s criticism of Mill.
supra, p. 472.
Capital imports and the terms of trade, 1931, Chap. V, for a discussion of this problem.
 or
or ?
?op. cit., p. 53, note.
(Capital imports and the terms of trade, 1931, pp. 98-100) discusses the type of index number to be used, but without reference to the influence of capital borrowings on the nature of the bias to be expected in the price indices according to the method of weighting used. He argues that when the world prices of Australia’s imports are rising, Australians will tend to increase in relatively greatest degree their imports of those commodities which rise least in price.
(Ibid.) This would be a valid presumption if the changes in relative prices were due primarily to the indirect effects on money costs abroad of capital movements or were due to relative changes in the world demands for the different commodities in which changes Australia did not participate, but it would not be a valid presumption if the relative changes in import prices were due primarily to relative changes in world demands in which changes Australia did participate.
Money credit & commerce, 1923, pp. 160-63, 338-40.
ibid., p. 339.
(ibid., p. 339) reproduced verbatim except for the modifications made necessary by my modification of his chart and except for a few minor verbal changes in the interest of clarity.
Quarterly journal of economics, XXXIX (1924), 144-50. The main theme of this article, however, was not the validity of the consumer’s-surplus notion, which was discussed only incidentally, but some apparent errors in computation in Marshall’s arithmetical illustration.
OG curve from
O, there occurs a change in the average utility significance of a G-bale if no change has meanwhile occurred in G’s utility functions. What the direction of this change will be will depend on the elasticity of the
OG curve, i.e., on whether a movement along the
OG curve from
O (and therefore an increase of surplus) is associated with an increase or a decrease in the amount of G-bales expected.
Papers relating to political economy, 1925, II, 31-47 (first published in
Economic journal, 1894).
Mathematical psychics, 1881, pp. 115-16.
supra, amount to the same thing.—Edgeworth, “On the application of mathematics to political economy,”
Journal of the Royal Statistical Society, LII (1889), 555-60.
infra, pp. 580-81.
Papers, II, 37.
OE, or country E’s reciprocal-demand curve, is inelastic, but not when
OE is elastic. In chart XVIII,
OE is elastic, so that this chart is according to Edgeworth applicable to both types of disturbances.
(Ibid., p. 38.)
papers, II, 22.
ibid., p. 39, fig. 6.
ibid., pp. 38, 71-72. Edgeworth remarks: “It is not contended that the exception is of any practical importance.”
(ibid., p. 72.)
The pure theory of foreign trade [1879], reprint 1930, p.I: cf. also
ibid., Money credit & commerce, p. 157:
Thus money, even when firmly based on gold, does not afford a good measure of international values, and it does not help to explain the changes in these values, which are caused by broad variations in international demand; but on the country it disguises and conceals them. For it measures changes in values by standards which are
automatically modified by the very variations in international demand, the effects of which are to be measured. (Italics are in original.)
Theory of international trade, 1936, p. 154:
The material difference between the two types of curves is that the Marshallian [foreign-trade] curves give a
complete picture, showing the final result of the whole international trade mechanism, and relate to
representative bales, while the ordinary [domestic-trade] curves relate to the
money prices of an
individual commodity, upon the assumption that other things remain equal and in particular that all other prices remain the same, so that they can give only a partial picture…”(Italics are is original.)
A geometrical political economy, 1904, p. 97. (But cf.
ibid., pp. 114 ff.)
See also T.O. Yntema,
A mathematical reformulation of the general theory of international trade, 1932, pp. 47-50. In a footnote
(ibid., p. 48) Yntema concedes that the foreign trade curves which he derives from domestic demand and supply curves in terms of money may not be equivalent to Marshall’s reciprocal demand curves:
This derivation is based on the assumption that the import demand price on its fixed-height schedule is a function only of quantity imported and that the export supply price on its fixed height schedule is a function only of quantity exported. Marshall’s comments on the interdependence of import demand and export supply seem to refer not to a functional interrelation of fixed-height schedules but to the interdependence which arises out of the necessity of balancing international debits and credits. Where a functional relation between fixed-height schedules does exist, Marshall’s curves are still applicable, but they cannot be derived from their component elements by two-dimensional graphs.
The “fixed-height schedules” referred to here are supply and demand schedules of two commodities in terms of adjusted money prices. Marshall nowhere explains the derivation of his reciprocal-demand curves from the complex factors operating within each economy. As Edgeworth comments: “A movement along a supply-and-demand curve of international trade should be considered as attended with rearrangements of internal trade; as the movement of the hand of a clock corresponds to considerable unseen movements of the machinery”
(Papers, II, 32). Marshall allowed the operations of the internal machinery to remain unseen, but since his reciprocal-demand curves relate to two “commodities” taken as constituting the entire range of commodities, it seems necessary to assume that Marshall would not have regarded the demand functions and the supply functions of these respective commodities within each country as independent functions.
The theory of international prices, 1926, p. 454: “First, the assumptions on which the [Marshallian foreign-trade] curves are based, and the limitations to which they are subject, are precisely the same as for composite demand and supply curves of the more familiar sort [i.e., the ordinary domestic-trade theory curves?]. The preference for them is based simply on their greater advantage, for certain purposes, as a graphic device.” Cf. also,
ibid., pp. 456-57: “The curves also permit an easy measurement of the direct benefits from trade….
Recharches sur les principes mathématiques de la théorie des richesses, 1838, pp. 173-81; Principes de la théorie des richesses, 1863, pp.316-24;
Revue sommaire des doctrines kconomiques, 1877, pp.196-213.
Recherches, 1838. My subsequent references are to the translation by N.T. Bacon:
Researches into the mathématical principles of the theory of wealth, 1927, pp. 150-57.
(Theory of international prices, p. 245), the only writer who finds sense and significance in Cournot’s thesis, it is made the basis for a defense of the validity of Cournot’s argument within the limits of his assumptions. But Cournot, in reply to Hagen, expressly rejects this interpretation and claims that his method of computation gives full consideration to any income resulting from a transfer to other employments of the resources released from the production of M. (Cournot,
Principes, 1863, pp. 329-30;
Revue sommaire, 1877, pp. 193-95, 205.) The only explanation I can offer, for which there seems some warrant in Cournot’s exposition, is that Cournot held that since the change in the price of M and in the money income of producers of M would affect the price and the incomes of the producers of any other one commodity only to a negligible extent, it was permissible to assume that the prices and the incomes of producers in country B of other commodities than M would remain unaltered, i.e., it was permissible to ignore items (3), and (4) above. (See Cournot,
Researches, pp. 130-32.) But this would be equivalent to saying that if the contents of a large tank of water were allowed to spread thinly over a great area, because at any one point the amount of water would be negligible, therefore the amount of water over the entire area could reasonably be regarded as negligible as compared to the amount of water originally in the tank.
Papers relating to political economy, 1925, II, 47-51; Bastable,
Theory of international trade, 4th ed., 1903, pp. 173-75; A. Landry,
Manuel d’économique, 1908, pp. 838-39; Irving Fisher, “Cournot and mathematical economics,”
Quarterly journal of economics, XII (1898), 130-32.
A geometrical political economy, 1904, pp. 48 ff. See especially his fig. 51,
ibid., p. 98, and compare it with the Barone diagrams referred to later in the text.
Grundzüge der theoretischen Nationalökonomie (German translation by Hans Staehle of the original Italian edition of 1908), 1927, pp. 101 ff. Barone does not refer to Cunynghame.
Grundzüge, fig. 30, p. 102, and fig. 32, p. 105.
CA, but would supply
TA from her own production.
AF, but would consume
AE herself.
(ibid., p. 102), but without indicating the nature of their shortcomings.
An algebraic formula introduced in 1904 by A. C. Pigon, applied statistically by Henry Schultz in 1928, and receiving authoritative acceptance today as the “correct method” of determining the effect of duties on prices and domestic output, is essentially an algebraic application of the Cunynghame-Barone graphical analysis. Frovided the method is used only to trace the effect on the price of a particular commodity of a change in the duty on that commodity, all other related circumstances meanwhile remaining substantially unchanged, it probably produces fairly reliable results, and does seem to me to be superior to other methods commonly used. The method would become seriously questionable, however, if applied to trace the effect on price of a substantial change in duty on a major commodity or group of commodities, since some of the factors supposed to be remaining unchanged in the
caeteris paribus pound would then actually be undergoing substantial change and these changes would react on the price of the commodity in question. The method would be even more suspect if it purported to serve as a means of measuring the amount of gain or loss to a country resulting from a tariff change, whether the change was a major or a minor one. For the nature of the formula, and an account of the literature relating to it, see Henry Schultz, “Correct and incorrect methods of determining the effectiveness of the tariff,”
Journal of form economics, XVII (1935), 625-41. Schultz makes clear that the results of the use of this formula become questionable if “the effect of the tariff on the prices of other commodities and on the balance of international payments [are] too great to be neglected”
(ibid., p. 641), which is certain to be the case when the tariff changes are major ones.
Untersnchungen über die Theorie des Preises, 1889, pp. 408-29. Cf. the comments of Edgeworth,
Papers relating to political economy, II, 58-60.
Appendix
