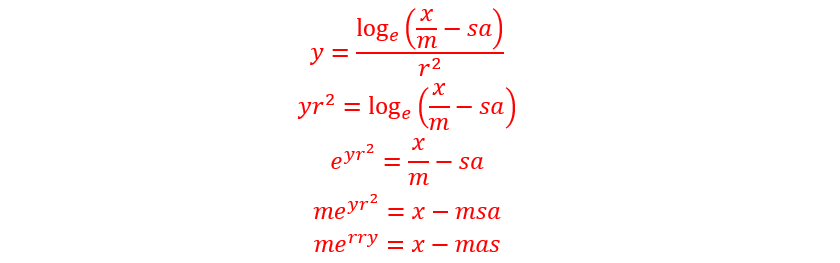
The person who derived “Merry Christmas” from a logarithmic function as shown on the accompanying image (relayed on Facebook by my economist friends Germain Belzile and Steve Ambler) had a stroke of poetic-mathematical genius. The derivation of the formula indirectly reminds us how mathematics is aesthetic. And it incites us (or at least me) to devote a few minutes of Christmas 2018 to ponder the controversial question, Is mathematics misused in economics?

I won’t answer the question, but only bring attention to a few related points. First, we should not confuse the use of mathematics in economic theory with its use in statistics and econometrics (I will speak about the former). Second, there is nothing wrong with not being economist or mathematician, and nobody can be Pico della Mirandola; yet, with regard to the question asked, we might lend more credibility to critics who know something about both mathematics and economics.

John Maynard Keynes had studied mathematics at Cambridge, but apart from attending lectures by the great Alfred Marshall, he had little formal training in economics–which did not prevent him from becoming one of the most famous economists of our times. Contrary to what some people seem to assume, Keynes used very little mathematics and was suspicious of its usefulness in economics. What he wrote on mathematics in his General Theory of Employment, Interest and Money (Macmillan, 1936) would be espoused by the typical Austrian economist:

It is a great fault of symbolic pseudo-mathematical methods of formalizing a system of economic analysis … that they expressly assume strict independence between the factors involved and lose all their cogency and authority if this hypothesis is disallowed; whereas, in ordinary discourse, where we are not blindly manipulating but know all the time what we are doing and what the words mean, we can keep “at the back of our heads” the necessary reserves and qualifications and the adjustments which we shall have to make later on, in a way in which we cannot keep partial differentials “at the back” of several pages of algebra which assume that they all vanish. Too large a proportion of recent “mathematical” economics are mere concoctions, as imprecise as the initial assumptions they rest on, which allow the author to lose sight of the complexities and interdependencies of the real world in a maze of pretentious and unhelpful symbols.

I don’t believe that Keynes was a very good economist, but Paul Samuelson certainly was. Samuelson also knew much mathematics. His 1947 book Foundations of Economic Analysis was instrumental in introducing mathematics in mainstream economic theory. The epigraph of the book quotes mathematician J. Willard Gibbs saying that “Mathematics is a language.” In a 1952 article (“Economic Theory and Mathematics—An Appraisal,” American Economic Review 42, pp. 56-66), Samuelson argued that anything written in mathematics was, in principle, translatable in English (or any other literary language), and vice versa:

Mathematics is language. Now I mean this entirely literally. In principle, mathematics cannot be worse than prose in economic theory; in principle, it cannot be better than prose—the two media are strictly identical. …

Any truth arrived at by way of mathematical manipulation must be translatable into words; and hence, as a matter of logic, could quite possibly have been arrived at by words alone. …

When we tackle [the problems of economic theory] by words, we are solving the same equations as when we write out those equations.

Samuelson admits that it might take a lot of time to develop a literary proof equivalent to a mathematical one. So mathematics is often convenient. “To get to some destinations it matters a great deal whether you go afoot or ride by train,” he writes. Another major advantage of mathematics is to formalize one’s reasoning, clearly identify the hypotheses, and make errors of logic easily discoverable:

The convenience of mathematical symbolism for handling certain deductive inferences is, I think, indisputable. It is going too far to say that mathematicians never make mistakes. Like everybody else, they can pull some awful boners. But it is surprising how rare pure mistakes in logic are. Where the really big mistakes are made is in the formulation of premises. Logic is no protection against false hypotheses; or against misinterpretation of reality; or against the formulation of irrelevant hypotheses. I think it is one of the advantages of the mathematical medium—or, strictly speaking, of the mathematician’s customary canons of exposition of proof, whether in words or symbols—that we are forced to lay our cards on the table so that all can see our premises.

Yet, Samuelson’s appraisal of the role of mathematics in economics was more balanced than his detractors and math haters often seem to think. As career advice to young economists about the mathematical method in economics, he suggested:

Without mathematics you run grave psychological risks. As you grow older, you are sure to resent the method increasingly. Either you will get an inferiority complex and retire from the field of [economic] theory or you will get an inferiority complex and become aggressive about your dislike of it. … The danger is almost greater that you will overrate the method’s power for good or evil. You may even become the prey of charlatans who say to you what Euler said to Diderot to get him to leave Catherine the Great’s court: “Sir, (a + bn)/n = x, hence God exists; reply!” And, like Diderot, you may slink away in shame.

This piece of typically heavy Samuelsonian humor refers to a likely apocryphal story about a prank that Euler would have played on Diderot. “The story is ludicrous,” says my historian friend Alan Kors. But it led us back to God and December 25: Merry Christmas!