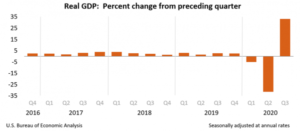
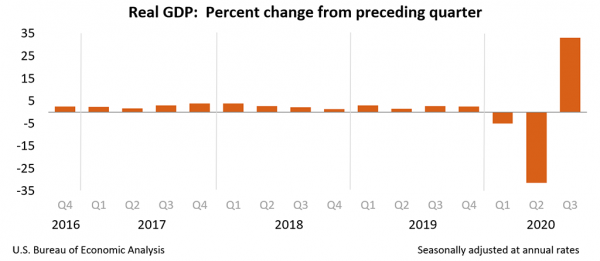
And the recovery is well under way.
Real gross domestic product (GDP) increased at an annual rate of 33.1 percent in the third quarter of 2020 (table 1), according to the “advance” estimate released by the Bureau of Economic Analysis. In the second quarter, real GDP decreased 31.4 percent.
This is from a news release from the U.S. Department of Commerce’s Bureau of Economic Analysis, October 29, 2020.
A 33.1 percent annual rate of increase means that that would be the rate if the rate of increase of the summer quarter continued for 3 more quarters. Of course, that won’t happen. To put it in perspective, a 33.1 percent annual increase implies that real GDP in the summer quarter increased by 7.4 percent. That’s a record increase for a quarter.
Of course it comes after the huge decline of 31.4 percent (annual) in the spring quarter, which happened due to Covid-19 and the lockdowns.
That doesn’t make it even. If a number falls by 31.4 percent, then to get back to where we where, we need an increase of 45.8 percent.
To help with the math on the second point a little, here’s how I put it after a tutorial during which I watched myself on video in prepping for my first distance-learning class way back in 2002: “The camera loses 1/4 of my energy; therefore I need to increase my energy by 1/3.”
Here’s the math on both if you’re interested and, for that matter, even if you aren’t interested.
Let x be the quarterly rate of growth.
Then (1+x)^4 = 1.331.
4 ln(1+x) = ln(1.331) = 0.2859
ln(1+x) = 0.2859/4 = 0.07148
1+x = e(0.07148) = 1.074
Therefore x = 0.074. Growth rate = 7.4 percent.
On the second one.
If a number falls by 31.4 percent, it falls to 68.6 percent of what it was.
To get from 68.6 percent to 100 percent, it must rise by 1/0.686 = 45.8 percent.

READER COMMENTS
AJ
Oct 30 2020 at 3:47pm
If everything presupposed in your math is accurate, then yes the recovery is underway.
David Henderson
Oct 30 2020 at 3:51pm
Or, almost equivalently: “If 2 + 2 still = 4, then yes, the recovery is underway.”
AJ
Oct 30 2020 at 4:08pm
Econ 101 makes simple assumptions like 2+2=4 to make claims like what you’re making. In reality, the assumptions you’re making are much more complex and subject to scrutiny.
Jon Murphy
Oct 30 2020 at 4:47pm
AJ, I don’t understand your point. “2+2 = 4” isn’t an assumption. The calculations of growth rates aren’t an assumption. It’s algebra.
AJ
Oct 30 2020 at 4:52pm
There aren’t any assumptions that go into growth rates? Nothing about culture, distribution of property rights, an understanding of how to make ‘optimal’ decisions, etc?
Jon Murphy
Oct 30 2020 at 5:11pm
No. Calculating growth rates, again, is a fairly straightforward procedure, as David shows.
It appears that you’re trying to critique the interpretation of GDP as a measurement of economic well-being? That’s all well and good, but it’s unrelated to the point being made in this post.
AJ
Oct 30 2020 at 5:24pm
This is a great dissatisfaction I’ve had in the economic way of thinking (GMU especially as a former graduate student). If economists can’t understand what they presuppose when they incorporate simple modeling assumptions to make bold claims about what ‘is’, for example, on growth rates, then there is a great poverty in their thinking.
Jon Murphy
Oct 30 2020 at 9:41pm
AJ, back up:
You are talking about something very different than what David Henderson is talking about. We are all well aware of the assumptions that go into models.
But this post is about growth rates and interpreting them. Thus David’s comment to you.
By the way, word of advice: if you think David Henderson is making a price theory mistake, think again. It is not something he is wont to do.
AJ
Oct 30 2020 at 9:54pm
Jon, the math works if all of the conditions going into the model are true. Are they in reality? Probably not. So David’s math, although economically correct, should in reality be taken with a big grain of salt.
Jon Murphy
Oct 30 2020 at 10:37pm
Math is not a function of the model. 2+2 = 4 is true regardless of whether the underlying assumptions of any given model holds.
Jon Murphy
Oct 30 2020 at 10:48pm
Here’s a quick example:
Take your standard Pigouvian model. The key assumption of that model is the omniscience of government.* One of the things Coase and other economists critical of the Pigouvian approach have since pointed out, that assumption does not hold.
In the Pigouvian model, 2 + 2 = 4. Does not follow that 2 + 2 =/= 4 in the Coasian model. Indeed, the equality of 2 + 2 = 4 is just as true in Coase as it is in Pigou. Coase’s story of the irrelevance of initial distribution of property rights in a costless world requires that the mathematics be the same!
So, AJ, your criticism that “the math works if all of the conditions going into the model are true” is logically and factually incorrect.
Now, if you want to argue that the current GDP numbers are not a good indication of true economic growth, that is fine. But note that is a very different point than the one being made here by David Henderson.
One final point: you seem to be equating mathematics with economics. You say:
The math is mathematically correct. You equate that with being “economically correct,” but your comments then imply that the mathematics are not economically correct; that the mathematics leave something economically important out. So, again, it’s not entirely clear what you are objecting to.
*Like Demsetz, I believe that transaction costs are not the main point of departure for Coase in his critique of the Pigouvian model.
AJ
Oct 30 2020 at 10:48pm
When you’re using mathematics to describe or make claims about human behavior, then a simplistic “2+2=4” is not the same thing as conditions that have to be assumed for these growth-rate equations to work. It’s the same difference between physicists who have to make assumptions for projectiles or objects dropped from a specific height vs economists who have to make assumptions about flesh and blood individuals to make claims about reality.
AJ
Oct 30 2020 at 10:58pm
I think I’m not explaining my point well. This is not the only key assumption that goes into economic models. So much is bound up in these models regarding the economist’s understanding of human nature, of culture, of preferences, of self-understanding of the individual, of etc that allow the economist to derive mathematic relationships and make claims about reality. My point is that if everything bound up in these models are true (which growth-rate equations are), then the output is true. In reality, the assumptions economists make to derive many of these relationships, I think, are worthy of being scrutinized as unrealistic, etc, so the output of modeling is a rough approximation of things, but that’s about it.
Jon Murphy
Oct 30 2020 at 11:12pm
That’s true but wholly irrelevant to David’s point. You need to understand that you are trying to shoehorn in this critique about modelling in a situation where it is irrelevant.
AJ
Oct 30 2020 at 11:15pm
This would be so much easier to talk through if I was still at GMU! I never met you while I was a grad student but talking in person would make conversations like this more productive. Clearly I cannot get my point across of my objections to David’s post, so I’ll leave it at this.
Richard A.
Oct 30 2020 at 4:38pm
The unit of the natural logarithm is called the neper (Np). If you multiply the neper by 100 you get the centineper (cNp). The cNp is very often superior to percentage.
Going from 1 to 2 represents a 100% increase, but going back to 1 from 2 is a 50% decrease. Going from 1 to 2 in cNp is 100ln(2) which equals 69.3 cNp and going back to 1 from 2 is 100ln(1/2) which also equals 69.3 cNp.
Alan Goldhammer
Oct 30 2020 at 5:04pm
James Hamilton has a good analysis of this over at Econbrowser.
Ashu
Oct 30 2020 at 6:43pm
How much of that growth do you think is caused by the federal reserve expansionary policy with the relief stimulus package compared to the US economy just trying to catch up to pre coronavirus levels.
Plus you could have done that math 10x easier. Just
(1+x)^4=1.331
(x+1)=1.331^(1/4)
x=1.331^(1/4)-1
saves you a lot of work from ln(x)
Lawrence Ludlow
Oct 31 2020 at 9:44am
That’s a good question. You have to wonder about the effect of the stimulus.
David Henderson
Oct 31 2020 at 10:55am
Thanks, Ashu. I’m from the “slide rule and carrying around thin books of natural logs” era.
Carl Folke Henschen Edman
Oct 30 2020 at 7:05pm
You forgot to deannualize the second number. Once you do that, the percentages become so small that the drop/rise almost ceases to matter.
Mark Brady
Oct 30 2020 at 7:31pm
“The COVID/Lockdown Recession Is Over. And the recovery is well underway.”
Yes, if we’re thinking of the recession and recovery as events through time.
But would we want to say in an unqualified fashion that when output began rising in early 1933, and continued rising until late 1937, the recession was over for that entire period? After all, the entire 1930s is often called the Great Depression.
David Henderson
Oct 31 2020 at 10:56am
Obviously I can’t predict the future.
Mark Brady
Oct 31 2020 at 6:01pm
Indeed. Neither you nor I nor anyone else can predict the future. But I’d be very surprised if the U.S. economy gets back to 2019 levels of GDP by, say, spring or even summer of next year.
Bill
Oct 30 2020 at 9:57pm
I believe there is a typo in the quarterly rate of growth demonstration:
ln(1+x) – 0.2859/4 = 0.07148 should read ln(1+x) = 0.2859/4 = 0.07148
David Henderson
Oct 31 2020 at 10:56am
Good catch. Correction made. Thanks, Bill.
john hare
Oct 31 2020 at 5:00am
Richard A has the simpler explanation above. Going from 100 to 50 is a 50% drop. But it then takes a 100% increase to reach 100 again.
When I’ve done this it was a one quarter drop from 100 gets down to 75 and is a 25% decrease. But then it takes a one third increase to get back to 100. Sometimes it is necessary to keep it simple with whole numbers to focus on communicating the concept instead of the algebra. You can explain this to people with four physical coins.
Sometimes I need to get various points across to people without a math background. Simple is good.
David Henderson
Oct 31 2020 at 10:57am
Yup.
Ted Durant
Nov 1 2020 at 12:39pm
It’s even easier to ignore quarterly changes in GDP and just look at the actual level. GDP per capita peaked at $66,064 in 2019Q4, fell to $65,430 2020Q1, $59,170 2020Q2, and came back to $64,043 in 2020Q3.In terms of change from peak, it was down 10% in Q2, and down 3% in Q3.
We’re still 33% below the post-WWII trend level in nominal per capita GDP.
David Seltzer
Nov 3 2020 at 5:41pm
High school Algebra.
To wit. 100 – 25 =75. 25%, decline.
75(1+x) = 100
1+x = 1.333
x =33.33%
QED
Greg Grialou
Nov 17 2020 at 2:22pm
Hmm…well, I don’t know why, but I’d submitted a response on this thread that SHOULD have been submitted before my comment 11/17/2929 2:09pm. Since it’s not available, I’ll reiterate here/now:
You can use all the mathematic equations you want to “prove” the recession is “over”. Statistically, you can prove anything (= Bullshit). Until “reality” bites you in the ass!
I’ve friends with doctorate degrees, VERY SMART people. Unfortunately, some of them think that because of their great intellect, schooling and degrees…they are always right! I’ve proved to them on occasion, that they are wrong.
Comments are closed.