According to the BLS, TV prices (olive green line) fell by 94.5% between 1997 and 2015:
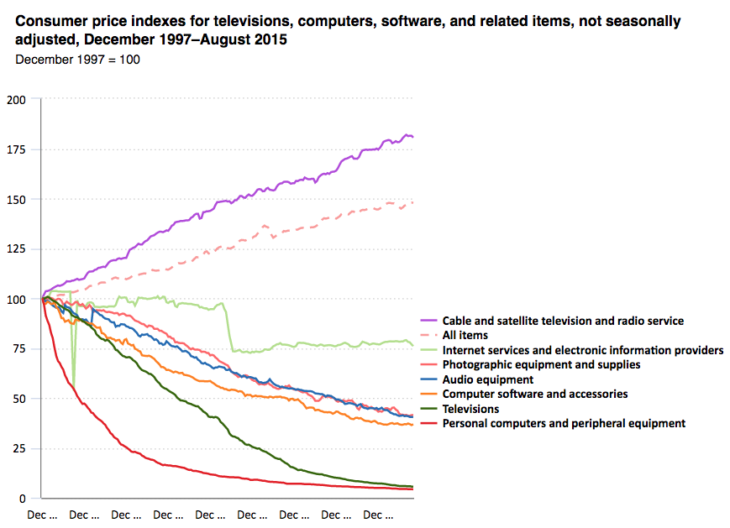
A TV set that cost $200 in 1997 cost $11 in 2015. Today the price would presumably be even lower. Try to imagine visiting your local BestBuy and asking to look at their $11 TV sets.
Of course, what’s actually going on here isn’t so much that people are spending less money of TV sets, rather that they are getting better TV sets when they spend $200 at the local retailer. But how much better? The BLS estimate suggests that a $200 TV set purchased in 2015 was 18.2 times better than a $200 set purchased in 1997. But what does that mean?
Does it mean the screen is 18 times larger? Does it mean that George’s foibles on Seinfeld are 18 times funnier on the 2015 TV set? Is a 9th inning home run in Yankee Stadium 18 times more thrilling on the 2015 TV set?
When I’ve raised this issue in the past, commenters have occasionally suggested that “revealed preference” provides some sort of objective way of ascertaining the subjective value of TV quality improvements. But that view is based on a misunderstanding of concepts like “willingness to pay” and “consumer surplus”.
For many decades, the TV market has generated a large amount of consumer surplus. People spend a lot of time watching TV, and would be willing to pay a fairly large sum for TV sets if they had to. But they don’t have to, because supply has increased sharply due to technological progress, and also because the industry is pretty competitive, with many sellers to choose from. So the price that people actually pay for a TV set doesn’t tell us how much value they derive from the set (except at the margin).
A slightly more sophisticated argument is that if one set sells for 10 times more than another set, then consumers must derive 10 times more value for the fancier set. Again, this is wrong. The people buying expensive TV sets are different from those who choose to buy cheaper sets. Why wouldn’t Bill Gates want to get the best TV set at almost any reasonable price?
Let’s say the average TV set is $200 (call it set A), and then manufacturers come out with a fancier set (B) that sells for $1000. Some people then (wrongly) assume that set B is viewed as 5 times better than set A. Eventually, the price of set B falls to $200. At that point, manufacturers come out with even fancier set C, which sells for $1000. Set C is (wrongly) viewed as 5 times better than set B, and by inference 25 times better than set A. Over time, the price of set C falls to $200. Now the BLS says that the price of TVs has declined by 96%, to only 1/25th of their original price.
The problem here is that the fact that set B sells for 5 times more than set A does not mean that it is 5 times better. For instance, my current TV set cost $7000. And yet I don’t view it as being 7 times better than a $1000 TV set. So why did I buy it? Because I do view it as being at least $6000 better than a $1000 set. Thus my maximum willingness to pay for a big $7000 OLED might well have been $107,000. And my maximum willingness to pay for a ordinary $1000 big screen might have been $100,000. In that case, even if I regarded the OLED as being only 7% better than an ordinary TV set, I’d prefer it at a price of $7000 over an ordinary TV selling for $1000.
The older I get, the less confident I am that we have any objective way to measure utility. Keynes (1936, Ch. 4) had the same view:
But the proper place for such things as net real output and the general level of prices lies within the field of historical and statistical description, and their purpose should be to satisfy historical or social curiosity, a purpose for which perfect precision — such as our causal analysis requires, whether or not our knowledge of the actual values of the relevant quantities is complete or exact — is neither usual nor necessary. To say that net output to-day is greater, but the price-level lower, than ten years ago or one year ago, is a proposition of a similar character to the statement that Queen Victoria was a better queen but not a happier woman than Queen Elizabeth — a proposition not without meaning and not without interest, but unsuitable as material for the differential calculus. Our precision will be a mock precision if we try to use such partly vague and non-quantitative concepts as the basis of a quantitative analysis.
BTW, Is there anything worse than an economist mocking the public for being consistently “biased” in their forecasts of inflation, as if economists have some sort of scientific way of ascertaining the “true” rate of inflation? Should we really be scolding the public for not understanding that since 1997 the price of a brand new $200 TV set has fallen to $11?
PS. On the other hand, the nominal aggregate expenditure on TVs is a relatively objective concept, and does have real meaning.
PPS. After his comments on the price level and real output, Keynes suggested that what we should actually be focusing on is the money value of income/output, and also the total level of employment. I agree.


READER COMMENTS
Andrew_FL
Jun 24 2021 at 2:55pm
I didn’t need to get old to come around to this view, I just had to read Menger.
Good post.
Thomas Lee Hutcheson
Jun 24 2021 at 3:20pm
But don’t we need at least an approximate optimal level of inflation in mind when we choose the optimal target for NGDP?
Scott Sumner
Jun 24 2021 at 4:53pm
No, we need an optimal NGDP growth rate.
Thomas Lee Hutcheson
Jun 26 2021 at 7:22am
But how do we estimate what the optimal NGDP target ought to be with no idea of what part of NGDP growth is “real?”
robc
Jun 24 2021 at 3:45pm
If you define inflation as change in M2 (or similar), then, yes, they do.
Scott Sumner
Jun 24 2021 at 4:55pm
If you define inflation as the DJIA, it’s also a precise concept. But since economists don’t define inflation that way, it’s a moot point.
robc
Jun 25 2021 at 12:42am
Maybe I have misunderstood, but didnt they used to? I thought that at one time “monetary inflation” not “price inflation” was the standard definition of inflation.
Scott Sumner
Jun 25 2021 at 1:28pm
I don’t think there was ever a time when inflation was defined as changes in M2. There was a time when some economists (not all) referred to a reduction in the price of gold as inflation.
robc
Jun 25 2021 at 10:07pm
What about during the gold standard era?
art andreassen
Jun 24 2021 at 4:19pm
Scott: I have a problem with economists using the BLS deflated industry shipments because of the distortion it causes to real dollar economic relationships. BLS measures of the real dollar values of outputs entail an estimate of a dollar value of the quality improvements of those TV’s. This value has no basis on any market transaction and has no offsetting value as a balance on the input side of the accounts. Economists use these real dollar values of shipments and GDP in their models and seem uninterested in the what distortions these inflated real dollars values have on the calculated variables.
Changes in productivity are compared to changes in wages where the outputs incorporate quality increases but the wages of course do not. Those quality increases don’t appear nowhere else. The BLS could easily calculate the total real dollar impact that the deflation process has on the value of real GDP.
Scott Sumner
Jun 24 2021 at 4:56pm
“The BLS could easily calculate the total real dollar impact that the deflation process has on the value of real GDP.”
Sorry, I don’t follow what you are saying here.
art andreassen
Jun 25 2021 at 2:07pm
Scott; In order for the BLS to calculate the PPI deflator for a product it compares the present market price with the base year market price. It attempts to insure that any changes in the quality of that item over the intervening period is reflected in the present price, i.e., any improvement in the item not deemed already included in the present price is added to the market price. The BLS uniquely estimates the value of these improvements and increases the real dollar value of the item by that amount. In other words, in the process of creating the deflator the BLS estimates a dollar value for each item for which there is an unpriced quality improvement not included in the market price. In the creation of the indexes the BLS has available for every item, industry and shipment the dollar value that it has increased real dollar value. It can therefore easily publish the dollar value change in real dollar GDP and real dollar industry shipments so that users of these data are aware of the BLS impact on them.
The BEA goes to inordinate extremes to estimate such items as Food Consumed on the Farm or the Inventory Value Adjustment, for example, which I bet are minute when compared with the economic impact of this quality adjustment on real GDP.
David Seltzer
Jun 24 2021 at 4:47pm
Scott, I was just thinking about this yesterday. I paid $2500 for a new Camaro coupe in 1967. Base model features were; six cylinder engine, radio, heater and 3 speed manual transmission. The price of that car today, using 4% average annual inflation 1967 to 2021 is 2500(1.04)^54 =20,785. A 2021 base Camaro lists for $25,000. The base model includes, a highly efficient 4 cylinder engine. 6 speed automatic transmission with O/D. ABS and drive line. A/C, LCD monitor and key Fob. The marginal difference is $4215. Subjective value suggests how useful those features are to the consumer. I haven’t considered how much safer the 2021 model is or better fuel mileage and lower insurance premia.
In a crude way, if I take the Ln of 25000/20785, I get .1846. dividing by 54 years, the annual increase is about .34%. Far below the rate of inflation. In the end, I suspect my thought experiment is somewhat trivial.
Scott Sumner
Jun 24 2021 at 4:58pm
Why are you comparing an inflation differential to the overall rate of inflation?
David Seltzer
Jun 24 2021 at 5:21pm
Scott, I’m not sure I understand your question. As I said the measure was crude. I’m not clear on the difference. Thanks
David Seltzer
Jun 24 2021 at 5:31pm
Scott: Now I understand your question. Mea Culpa.
Dylan
Jun 24 2021 at 4:59pm
Yeah…but a ’67 Camaro was cool…
David Seltzer
Jun 24 2021 at 5:22pm
Dylan. I loved the car. My first new car.
David S
Jun 28 2021 at 5:42pm
Dylan is right. Any Camaro from the 60’s has a coolness value that exceeds any modern American sports car by orders of magnitude. It’s hard to measure the loss of style, but the decline started in the 80’s.
Jason
Jun 24 2021 at 5:08pm
A $200 TV from 1997 in perfect condition might have a market value of $11 today. In that sense the deflator seems appropriate. In terms of utility it’s difficult to argue that TV is 18 times more enjoyable with a modern TV.
Scott Sumner
Jun 24 2021 at 10:22pm
Jason, You said:
“In that sense the deflator seems appropriate.”
But appropriate for what purpose? I don’t think that many people set aside $11 to go to BestBuy and purchase a TV, even one of 1997 quality (which actually wasn’t all that bad.) It’s a thought experiment without clear practical implications. For instance, we use the CPI to adjust Social Security. Are we telling old people to go to the store and buy a $11 TV?
MarkW
Jun 24 2021 at 10:26pm
A TV vastly better than anything available in 1997 has a *negative* market value today. I have a couple of extra 32″ 1080P TVs left by my kids when they moved out. They’re still here because it would cost me at least $25/each to recycle. Maybe somebody will want them sometime, plus I’m lazy.
Along with those ‘vastly better than anything available in 1997’ TVs, I’ve got some old but vastly better than ’97 smart phones, digital cameras, and laptops laying around that could use (but won’t find) a good home.
Scott Sumner
Jun 25 2021 at 1:30pm
I had to pay workers $25 to take away some big old CRT TVs.
Brian
Jun 24 2021 at 8:04pm
If there had been a steady market for the goods of 1997, the 1997 TV would not have been priced at $11 in 2015. For a TV to be worth 200 USD in 1997 meant it had a CRT so that part alone would have made it cost more than $11 in 2015.
It is implausible that a big heavy tube of glass and some embedded electrodes and a phosphor pattern would be priced at retail at $11 in 2015. Just the cost of shipping and handling the item multiple times from the component maker to the assembly plant to the distributor to the big box retailer would seem to cost a big part of the $11.
This means we should be skeptical about interpreting quality improvements as an increase in utility and therefore a decrease in price for the original amount of utility. Your skepticism about measuring utility is well founded. (I don’t mind the practice of equating utility to dollars within a limit.)
The price of a thing is completely dependent upon the context. People always mention the context includes utility and technology and competition. An important factor sometimes overlooked is that the price is very dependent upon the evolution or “path” of the allocation of production resources. More investment in production leads to a lower price. This can happen in the opposite way. Since we don’t want to make CRTs anymore, it will cost much more than $200 to retail a 1997 TV in 2021 because it would have to be custom made. So the BLS is wrong to say there has been price decrease in TVs. Furthermore I do not want to say there has been price increase in TVs.
The safest thing to say, as I already wrote elsewhere, is that there is no such thing as a TV set. The 1997 TV is incomparable. The 2015 TV is incomparable. This is why the “TV set” as a time continuous concept does not exist.
J Mann
Jul 1 2021 at 12:47pm
I’d be very surprised if you could sell many 1997 TVs today at $25. $11 sounds within the range of reason to me, maybe $20.
Jairaj Devadiga
Jun 24 2021 at 9:09pm
Should we really be scolding the public for not understanding that since 1997 the price of a brand new $200 TV set has fallen to $11?
No. Instead, we should explain to them in a simpler manner. In 1959, a person earning the average wage at the time would need to work 127.8 hours to buy a colour TV. In 2013, a person earning the average wage had to work 20.7 hours for a colour TV (which was much better too).
Price changes over time are much easier to comprehend when explained in terms of how many hours one must work to be able to purchase any good or service.
Scott Sumner
Jun 24 2021 at 10:24pm
You said:
“Instead, we should explain to them in a simpler manner. In 1959, a person earning the average wage at the time would need to work 127.8 hours to buy a colour TV. In 2013, a person earning the average wage had to work 20.7 hours for a colour TV (which was much better too).”
I agree. This is a sensible explanation.
MarkW
Jun 25 2021 at 2:09pm
In 1959, a person earning the average wage at the time would need to work 127.8 hours to buy a colour TV. In 2013, a person earning the average wage had to work 20.7 hours for a colour TV (which was much better too).
Don Boudreaux did a lot of these kinds of comparisons with his 1976 Sears Catalog. (and somehow another 15! years have passed since that blog post — sigh). One very interesting aspect of his comparison was that the dramatic drop in prices (in terms of hours of work needed) applied to all kinds of goods, not just tech items — freezers, clothing, bedding, power tools, paint, tires. The prices decreases and quality improvements happened across the board.
Frank
Jun 26 2021 at 11:11pm
That measures relative changes in relative prices divided by the the relative change in labor productivity. A fascinating set of numbers, but nothing to do with inflation.
Njnnja
Jun 25 2021 at 9:03am
While hedonic adjustment is clearly more art than science, it’s not completely silly. How about a $1.25 TV? As Tyler Cowen would say, Markets in Everything…
https://www.ebay.com/itm/224503773253?epid=48202254&hash=item344577b845:g:BCwAAOSwBbNgznxr
Scott Sumner
Jun 25 2021 at 1:31pm
Check the shipping cost.
Njnnja
Jun 25 2021 at 4:42pm
The fact that they explicitly break out shipping is great for analytics 🙂
Inflation on consumer electronics: -99% (approx.)
Inflation on transporting a 20 lbs widget: 2%/year (approx.)
MarkW
Jun 26 2021 at 10:49am
But those aren’t real shipping costs. Grossly inflating shipping and handling costs is a tactic online vendors often use so that they can advertise a lower price (and end up higher in the results) in shopping search engines.
Njnnja
Jun 26 2021 at 11:43pm
Do people really find it hard to believe that old televisions are available for purchase for less than $10? Sure in one sense it mathematically matters if it is $11, or $5, or $1.25, since deflation is -7%, -10%, -25% (or whatever) per year, but in a practical sense I think the thing at issue here is the existence of somewhat extreme deflation in consumer electronics, which is quite well supported.
https://losangeles.craigslist.org/wst/ele/d/santa-monica-sylvania-lcd-color-tv/7340027790.html
J Mann
Jul 1 2021 at 12:44pm
As I said below, you can find old TVs on local shopping sites like facebook market or nextdoor for essentially free. (Again, you need to go pick them up, but if they’re local, presumably that’s only a few dollars.)
One reason shipping costs are high on old TVs is presumably that they are large and fragile – you can’t just wrap them in brown paper and put an address on them.
Brian
Jun 27 2021 at 5:19pm
Used TVs are supposed to have low prices. This example is from the used TV market so it probably has minimal relevance to the discussion of BLS measures inflation. I think used cars and used trucks are the only “used” categories used by the BLS. I guess they think the used market, aside from vehicles, is small.
J Mann
Jul 1 2021 at 12:45pm
Why would you think a used 1990 TV would provide much less utility than a new 1990 TV delivered today? Presumably it has a lower expected lifespan, but if so, double the price.
Brian
Jul 1 2021 at 5:54pm
My reply was in response to somebody that said quality (hedonic) adjustment is not completely silly. My contrary stance should not be taken to mean that I think it is completely silly. In fact I think it’s okay for inflation measures from a year to the very next year. In other words, there is a useful category called “TV sets” that includes 1997 TVs and 1998 TVs. Strictly speaking there is a problem but to measure inflation we need to be less strict.
However the BLS chart contains some nonsense in that they are reiterating the process over 18 years to seem to be making the point that a 1997 TV newly manufactured in 2015 would retail for $11 because of the change in the value of money. This is implausible for commonsense reasons.
I think you have said a used 1997 TV can sell for between $0 and $20 so you think $11 is reasonable so perhaps that is a defense of the BLS chart. I just think that’s not relevant because I don’t think the BLS is trying to plot the price of a 1997 TV that is aging. I would bet that the “used car and trucks” category is also not trying to measure the price of aging vehicles. I think they pick some standard like “5 year old vehicles”. So they would compare a 5 year old vehicle in 1997 made in 1992 and a 5 year old vehicle in 1998 made in 1993. The category would have it that it is 5 years old. Using the 1992 vehicle in 1998 would exclude it from the category because the age is 6.
You asked what I think of the utility of a used 1990 TV and a new 1990 TV made today. I think the lack of warranty is an important consideration as well as shorter expected life so may be I would make the ratio of their prices 10:1 or 2:1 depending upon how rough the aged one is. It has been many years since I owned a TV so I guess the used one creates zero utility for me and the new one is worth 10 times zero utility. The category “TV set” does not exist for large time spans.
J Mann
Jul 1 2021 at 12:42pm
I have the curious experience that I recall saying some extremely smart things one of the times Scott raised this issue on TheMoneyIllusion, but I can’t find or remember them. Let me try again.
First, you can in fact get an $11 tv. Go on craigslist or facebook market, and you will find people who will give you a 30+ inch old style tube tv if you agree to take it away – they would feel lucky to get $11. (Yes, it’s not as reliable as a new 1990s TV would be, and the repair options are more limited, but if it breaks, you can probably get a replacement for free, so I’m going to handwave reliability and repair availability concerns.)
It’s not like we can’t tell anything about someone who buys a $1000 TV’s utility. We can tell that they prefer a $1000 modern TV to an essentially free 1990s TV + $1000 or so. To figure out how much utility they’re getting, we need to look at their next best uses for $1000, not compare the TVs.
Comments are closed.