There’s an old story about a mathematician asking Paul Samuelson for one idea in economics that was simultaneously true and not obvious.  Samuelson’s answer is here.  Today, I’ve got another: The Chamley-Judd Redistribution Impossibility Theorem.  

Chamley and Judd separately came to the same discovery: In the long run, capital taxes are far more distorting that most economists had thought, so distorting that the optimal tax rate on capital is zero.  If you’ve got a fixed tax bill it’s better to have the workers pay it.  You can search the web for details and qualifications of their result, here’s Yglesias:
The standard “classic” result in this field is, in fact, that an optimal system would have no taxation of investment income. 
He turns to a collection of counterarguments by Piketty and Saez, concluding:
That’s a bit of an exotic argument, but if you want to undermine the standard approach there you have it. 
There, indeed, you do. 

Why isn’t Chamley-Judd more central to economic discussion? Why isn’t it part of the canon that all economists breathe in?  Why isn’t it in our freshman textbooks?  Part of the reason is surely mood affiliation–it’s an uncomfortable result for some to talk about as evidenced by the handwringing I see in most textbook treatments (exception here, big PDF, p.451). The result can’t be waved away as driven by absurd assumptions: It’s not too fragile, it’s too solid. It’s OK to teach Real Business Cycles since we all know (or “know”) that the Federal Reserve and aggregate demand really drive things in the short run.  But to tell people that if we care about the long run, the tax on capital income–on interest, profits, dividends–should be zero?  And to have only “exotic” counterarguments?  Let’s just leave that for the more advanced courses….

But another reason is just that the proof is too opaque.  I’ve worked it out a few times and while I can see the answer, I don’t really get it the way I do with comparative advantage or the equity premium puzzle or Arrow’s Impossibility Theorem.  
So I decided to take a first step at trying to fix that.  First, let me sum up a key implication of Chamley-Judd: 
Under standard, pretty flexible assumptions, it’s impossible to tax capitalists, give the money to workers, and raise the total long-run income of workers.    

Not, hard, not inefficient, not socially wasteful, not immoral: Impossible. 

If you tax capital income and hand all of the tax revenue to workers, then in the long run (or the “steady state”) you’ll wind up with a smaller capital stock. And since workers use the capital stock to earn their wages, the capital tax pushes down their wages.  
So far so obvious, standard supply-side stuff. At this point, you’re probably guessing that sometimes the taxes you hand to workers are more than the fall in wages, sometimes it’s less…it all depends on the assumptions, depends on the tax rate, depends on this or that.  But the magic of Chamley-Judd is that they proved that “fall in wages > rise in transfer” is a pretty stable result…hence the need for “exotic” counterarguments.  
Rational workers would rather have the extra machines to work with rather than a transfer from a tax on capital, thank you very much. 
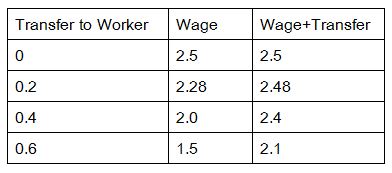
Rather than offer you a proof of the result, I offer you an Excel simulation of two economies, one where capitalists pay taxes to workers, and another where the society is taxless. I use standard assumptions, only the usual number of rabbits going into the hat.  Check and see which economy gives the highest total income (wages + transfer payments) to the working class.  Here are a few examples; note that wages fall by more than the rise in the transfer payment: It’s impossible to redistribute total income to workers:
ChamleyJuddExample.JPG
You can tinker with the numbers yourself in the Excel simulation: Change the degree of patience in the society (that changes the savings rate and hence the long-run capital stock) or change the size of the transfer payment to the proletariat (don’t make it too big or it’ll be impossible to pay the bill).  Every time you change the numbers, the Excel simulation tells you whether the Chamley-Judd result holds: It either reports “C-J Vindicated” or “C-J Fail.”  Let me know if you can make their theorem fail.  
I wrote up a derivation of the result here, two pages, some algebra, and a link to an extra Excel simulation. I welcome further attempts to popularize Chamley-Judd; Landsburg does a good job here. 
One big lesson I draw from Chamley-Judd: Good economic policy doesn’t try to do things that are impossible.  And if the world works roughly the way Chamley and Judd assume it does, a long run policy that redistributes total income from capitalists to workers is impossible.