The Theory of Interest
By Irving Fisher
THE tremendous expansion of credit during and since the World War to finance military operations as well as post-war reparations, reconstruction, and the rebuilding of industry and trade has brought the problems of capitalism and the nature and origin of interest home afresh to the minds of business men as well as to economists. This book is addressed, therefore, to financial and industrial leaders, as well as to professors and students of economics.Inflation during and since the War caused prices to soar and real interest rates to sag in Germany and other nations far below zero thus impoverishing millions of investors. In all countries gilt-edge securities with fixed return became highly speculative, because of the effect of monetary fluctuations on real interest rates. After the War the impatience of whole peoples to anticipate future income by borrowing to spend, coupled with the opportunity to get large returns from investments, raised interest rates and kept them high. Increased national income has made the United States a lender nation. At home, real incomes have grown amazingly because of the new scientific, industrial, and agricultural revolutions. Interest rates have declined somewhat since 1920, but are still high because the returns upon investments remain high. Impatience to spend has been exemplified by the organization of consumers’ credit in the form of finance companies specially organized to accommodate and stimulate installment selling and to standardize and stabilize consumption…. [From the Preface]
First Pub. Date
1930
Publisher
New York: The Macmillan Co.
Pub. Date
1930
Comments
1st edition.
Copyright
The text of this edition is in the public domain.
- Dedication
- Errata
- Preface
- Suggestions to Readers
- Part I, Chapter 1
- Part I, Chapter 2
- Part I, Chapter 3
- Part II, Chapter 4
- Part II, Chapter 5
- Part II, Chapter 6
- Part II, Chapter 7
- Part II, Chapter 8
- Part II, Chapter 9
- Part III, Chapter 10
- Part III, Chapter 11
- Part III, Chapter 12
- Part III, Chapter 13
- Part III, Chapter 14
- Part IV, Chapter 15
- Part IV, Chapter 16
- Part IV, Chapter 17
- Part IV, Chapter 18
- Part IV, Chapter 19
- Part IV, Chapter 20
- Part IV, Chapter 21
- Appendix to Chapter I
- Appendix to Chapter X
- Appendix to Chapter XII
- Appendix to Chapter XIII
- Appendix to Chapter XIX
- Appendix to Chapter XX
- Appendix to Chapter XX
§1. Introduction
PART III, CHAPTER XIV
THE THIRD APPROXIMATION UNADAPTED TO MATHEMATICAL FORMULATION
THE second approximation fails to conform to conditions of actual life chiefly with respect to risk. While it is possible to calculate mathematically risks of a certain type like those in games of chance or in property and life insurance where the chances are capable of accurate measurement, most economic risks are not so readily measured.
*30
To attempt to formulate mathematically in any useful, complete manner the laws determining the rate of interest under the sway of chance would be like attempting to express completely the laws which determine the path of a projectile when affected by random gusts of wind. Such formulas would need to be either too general or too empirical to be of much value.
In science, the most useful formulas are those which apply to the simplest cases. For instance, in the study of projectiles, the formula of most fundamental importance is that which applies to the path of a projectile in a vacuum. Next comes the formula which applies to the path of a projectile in
still air. Even the mathematician declines to go beyond this and to take into account the effect of wind currents, still less to write the equations
for the path of a boomerang or a feather. If he should do so, he would still fall short of actual conditions by assuming the wind to be constant in direction and velocity.
Scientific determination can never be perfectly exact. At best, science can only determine what
would happen under
assumed conditions. It can never state exactly what does or will happen under actual conditions.
*31
We have thus far stated verbally, geometrically, and algebraically the laws determining interest under the simpler conditions first, when it was assumed that the income streams of individuals were both certain and fixed in amount, but variable in time shape, and, secondly, when it was assumed that the income streams were certain, but variable in amount as well as in time shape. We have also considered verbally the interest problem under conditions of risk found in the real world.
§2. The Six Sets of Formulas Incomplete
All that I shall attempt here is to point out the shortcomings of the six sets of formulas in the second approximation. Impatience Principle A in the second approximation is expressed by formulas of the type:
F (
y‘ +
x‘,
y” +
x”,…,
y(
m) +
x(
m))
indicating that a person’s impatience is a function of his income stream as specifically scheduled, indefinitely in the future.
Of course, in the uncertainties of actual life no such specific scheduling is possible. The equation is true but incomplete, as
f is properly not only a function of one expected
income program but of many possible such programs each with its own series of probabilities, and those probabilities are too vague even to be specifically expressed or even pictured by the person concerned. That is, the average person is merely aware that he is willing, say, to pay five per cent for a $1000 loan because he thinks his future prospects will justify it. He vaguely expects that his present $10,000 income will probably rise to $20,000 within a few years, possibly to $30,000—and possibly not rise at all. He could think of innumerable possibilities and these would imply many other variables than those above cited. Much might depend on the income of others besides himself and on the future size of his family, the state of their health, and other conditions without end. His own future income is the important matter, but that itself is dependent on all sorts of variables on which he will reckon summarily in a rule of thumb fashion.
We could, formally, rewrite for the third approximation the above equation so as to read:
F ()
merely refusing to attempt any enumeration of the innumerable variables inside the parentheses—among them being, perhaps, all the variables included in all the equations in the second approximation, including rates of interest as well as numberless other variables such as probabilities not there included. In so far as the latter, or new, variables enter, each of them requires a new equation in order to make the problem determinate. Such new equations would be merely empirical. Among the equations which would be needed, would be those expressing the
y‘s and
x‘s in terms of real income—that
is, as the sum of the enjoyable services, each multiplied by its price. This would lead us into the theory of prices and the general economic equilibrium.
Impatience Principle B was expressed in the second approximation by formulas of the type:
f.
But now we must face not only one
i but a series of
i‘s, according as the market is the call loan market, the 60 to 90 day commercial paper market, the gilt-edge bond market, the farm mortgage market, and innumerable others, for each of which there is its own separate
f and
i.
These many magnitudes, including the
i‘s, require still other empirical equations impossible to formulate satisfactorily, albeit we know in a general way that the rate on gilt-edge bonds is lower than on risky bonds, the rate on first mortgages lower than that on second mortgages, and that the long term and short term markets do influence each other. But these relations are too indefinite to be put into any equations of real usefulness, theoretical or practical.
Investment Opportunity Principle A was expressed by formulas of the type
y‘,
y”,…,
y(
m)) = 0
This becomes
where the blank parenthesis stands for a multitude of unknowns (and unknowables) which could be discussed ad
infinitum and each of which, in so far as it was not already included among the variables entering into our system of equations, would require a new empirical equation of some sort in order that the problem shall be determinate. Moreover, the
f equation representing a
man’s ensemble of income opportunities is a composite of separate opportunities, the full and detailed expression of which would take us again into the theory of prices and general economic equilibrium.
Investment Opportunity Principle B, expressed in the second approximation by equations of the type
r,
would have to be replaced by as profuse a variety as replaced the
i =
f above.
A full statement of the margins of investment opportunity would include the margins of numberless individual enterprises and adjustments in the use of every item of capital. It would again lead us into the theory of prices and general economic equilibrium. Walras and Pareto have formulated systems of equations which do this and in which the theory of interest is merely a part of a larger whole.
Market Principle A, expressed in the second approximation by equations of the type
x2 +…. +
xm = 0,
will remain true only if or in so far as performance of contracts corresponds to promises and expectations. In so far as, because of defaults, the equations fail of being precisely true, no useful mathematical relation expressing that failure seems possible.
The same is true of Market Principle B, expressed under the second approximation by formulas of the type
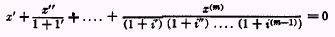
to say nothing of the fact that this type of equation will take many different forms in view of the variety of
i’s and in view of the probability factors.
The only explicit practical inclusion of such probability factors, mathematically, is to be found in the formulas of life insurance actuaries. But these are of little more than suggestive value in our present effort to express the determination of the rate of interest.
§3. Conclusions
We must, therefore, give up as a bad job any attempt to formulate completely the influences which really determine the rate of interest. We can say that the system of equations which has been employed
would fully determine the rate of interest were it not for disturbing factors; that it
does do so in combination with those disturbing factors; and that this amounts to saying that it expresses the fundamental tendencies underlying those disturbing factors.
In short, the theory of interest in this book merely covers the simple rational part of the causes actually in operation. The other or disturbing causes are those incapable of being so simply and rationally formulated. Some of them may be empirically studied and will be treated in Chapter XIX. They pertain to statistics rather than to pure economics. Rational and empirical laws in economics are thus analogous to rational and empirical laws of physics or astronomy. Just as we may consider the actual behavior of the tides as a composite result of the rational Newtonian law of attraction of the moon and the empirical disturbances of continents, islands, inlets, and so forth, so we may consider the actual behavior of the rates of interest in New York City as a composite of the rational laws of our second approximation and the empirical disturbances of Federal Reserve policy together with numberless other institutional, historical, legal, and
practical factors. All of these are worthy of careful study but are not within the scope of the main problem of this book.
In some cases, as in the theory of the moon’s motions, the perturbations may be worked out with a high approximation to reality by combining rationally a number of elementary influences. Such resolution of empirical problems represents the highest ideal of applied science. But until that stage is reached there remains a wide gap between rational and empirical science, and the two have to be pursued by somewhat different methods. That is the case with economic science in most of its problems today.
*32
In respect to our present problem, while there is a great field for research, the only perturbing influence of transcendent importance is that of an unstable monetary standard, and, as was seen in Chapter II, even that would make nothing more than a nominal difference in the results if it were not for the “money illusion.”
But with respect to this disturbance, theory and practice are miles apart. The disturbances of unstable money often reverse the normal operation of those supposedly fundamental forces which determine the rate of interest and are the chief subject of our study in this book.
The Nature of Capital and Income, Appendix to Chapter XVI.
Economics as a Science, in Proceedings of the American Association for the Advancement of Science, Vol. LVI, 1907.
Quantitative Analysis in Economic Theory. American Economic Review, Vol. XV, No. 1, March 1925, pp. 1-12.
Part IV, Chapter 15
