The Theory of Interest
By Irving Fisher
THE tremendous expansion of credit during and since the World War to finance military operations as well as post-war reparations, reconstruction, and the rebuilding of industry and trade has brought the problems of capitalism and the nature and origin of interest home afresh to the minds of business men as well as to economists. This book is addressed, therefore, to financial and industrial leaders, as well as to professors and students of economics.Inflation during and since the War caused prices to soar and real interest rates to sag in Germany and other nations far below zero thus impoverishing millions of investors. In all countries gilt-edge securities with fixed return became highly speculative, because of the effect of monetary fluctuations on real interest rates. After the War the impatience of whole peoples to anticipate future income by borrowing to spend, coupled with the opportunity to get large returns from investments, raised interest rates and kept them high. Increased national income has made the United States a lender nation. At home, real incomes have grown amazingly because of the new scientific, industrial, and agricultural revolutions. Interest rates have declined somewhat since 1920, but are still high because the returns upon investments remain high. Impatience to spend has been exemplified by the organization of consumers’ credit in the form of finance companies specially organized to accommodate and stimulate installment selling and to standardize and stabilize consumption…. [From the Preface]
First Pub. Date
1930
Publisher
New York: The Macmillan Co.
Pub. Date
1930
Comments
1st edition.
Copyright
The text of this edition is in the public domain.
- Dedication
- Errata
- Preface
- Suggestions to Readers
- Part I, Chapter 1
- Part I, Chapter 2
- Part I, Chapter 3
- Part II, Chapter 4
- Part II, Chapter 5
- Part II, Chapter 6
- Part II, Chapter 7
- Part II, Chapter 8
- Part II, Chapter 9
- Part III, Chapter 10
- Part III, Chapter 11
- Part III, Chapter 12
- Part III, Chapter 13
- Part III, Chapter 14
- Part IV, Chapter 15
- Part IV, Chapter 16
- Part IV, Chapter 17
- Part IV, Chapter 18
- Part IV, Chapter 19
- Part IV, Chapter 20
- Part IV, Chapter 21
- Appendix to Chapter I
- Appendix to Chapter X
- Appendix to Chapter XII
- Appendix to Chapter XIII
- Appendix to Chapter XIX
- Appendix to Chapter XX
- Appendix to Chapter XX
§1. Eligible and Ineligible Options
PART II, CHAPTER VII
THE INVESTMENT OPPORTUNITY PRINCIPLES
THE essential point of the preceding chapter is that the possibility of more than one use of our resources affords opportunity to invest by substituting one such use for another. Whenever there is such a choice of alternatives, as for instance by changing from the “mining” to the “farming” use of one’s land, as per Table 3, there is a differential sacrifice or investment of income during the earlier years for the sake of a differential return later. The fact that such alternative uses of labor, land, and capital exist, introduces on the scene the whole subject of “productivity”.
Böhm-Bawerk was profoundly right when he wrote:
“The statement of how the productivity of capital works into and together with the other two grounds of the higher valuation of present goods, I consider one of the most difficult points in the theory of interest, and, at the same time, the one which must decide the fate of that theory.”
*61
I have generally avoided the term productivity of capital because it may be used ambiguously to mean physical productivity, or value return, or return over costs; and because it suggests that capital produces income value instead of the reverse; and because it attributes the
value of manufactured things to the cost of production, instead of to their discounted future services.
I prefer the term investment opportunity. It has some of the demerits as well as the merits belonging to any new term. It is unfamiliar and therefore requires precise definition. The concept of investment opportunity rests on that of an “option.” An option is any possible income stream open to an individual by utilizing his resources, capital, labor, land, money, to produce or secure said income stream. An investment opportunity is the opportunity to shift from one such option, or optional income stream, to another.
It includes all possible opportunities to invest—those that can yield only negative returns upon the investment as well as those which are capable of yielding very large surpluses over the amount of the investment or cost.
The first (A) of the two investment opportunity principles specifies a given range of choice of optional income streams. Some of the optional income streams, however, would never be chosen, because none of their respective present values could possibly be the maximum. We have seen that the land, in our example, would be most profitably employed for farming, for mining, or for forestry, according to the rate of interest. But it would not be employed, let us say, for a quarry, no matter what might be the rate of interest.
The optional uses which are thus out of the question, whatever be the rate of interest, are called
ineligible. The rest are the
eligible options. We need to consider the eligible ones—any one of which might be made to have the maximum present value, given the right rate of interest to make it so.
§2. The Method of Comparative Advantage
The second (B) investment opportunity principle, that of maximum present value, is of great importance and has many aspects not always recognized as related to one another. Let us restate this maximum value principle in an alternative form, thus: one option will be chosen over another if its income possesses comparative advantages outweighing (in present value) its disadvantages.
To illustrate this alternative method of stating the same principle—which method might be called the method of comparative advantage—let us recur to the example of the land. We found that, when the rate of interest was 4 per cent, the owner would elect the forestry use, since this possessed the greatest present value. If we now compare, year by year, the income from the land when used for forestry purposes with the income which it might have yielded if used in one of the other ways, as for instance farming, we shall see that in some years there is an excess in favor of the forestry use, and in other years a deficiency, as shown in the table on the following page.
Here we see that, in the first four years, there are comparative disadvantages, a differential sacrifice, amounting in the four respective years to $450, $450, $150, $50. These are the disadvantages from the use of the land for forestry purposes as compared with its use for farming, but the disadvantages are offset later by advantages in return amounting to $50 each year perpetually. If prior to the first year listed above the owner has been using the land for farming purposes and was considering the advisability of changing over to forestry, he would think of the disadvantages or sacrifices of $450, $450, $150 and $50
as investments or costs and the advantages of $50 each year in perpetuity as returns on these investments or costs. And he could think of the proposal to substitute the forestry use for the farming use as an
opportunity to invest the $450, $450, $150, and $50 for the sake of securing the return of $50 each year thereafter. If, now, we take the total present value, at 4 per cent, of the deficiencies, or
investments, of $450, $450, $150, and $50, we shall obtain $1025, whereas the present value of the returns of $50 per annum beginning in five years and continuing in perpetuity will be $1069. Thus the present value (at 4 per cent) of the gains exceeds the present value of the sacrifices or costs by the difference between $1069 and $1025. As reckoned in present estimation, the gains of income outweigh the costs or sacrifices of income. We may say, therefore, that, the rate of interest being 4 per cent, forestry is preferable to farming because of a surplus of advantages over disadvantages reckoned in present value. Thus, the opportunity to invest by
switching over from farming to forestry is, if money can be borrowed at 4 per cent, more than worth while.
| TABLE 6 Farming and Forestry Use Compared by Method of Comparative Advantage |
|||
|---|---|---|---|
| Annual Value of Farming Uses
|
Annual Value of Forestry Uses
|
Difference in Favor of Forestry Use
|
|
| 1st year | $450 | … | -$450 |
| 2nd year | 450 | … | -450 |
| 3rd year | 450 | $300 | -150 |
| 4th year | 450 | 400 | -50 |
| 5th year | 450 | 500 | +50 |
| 6th year | 450 | 500 | +50 |
| 7th year | 450 | 500 | +50 |
| 8th year | 450 | 500 | +50 |
| 9th year | 450 | 500 | +50 |
| 10th year | 450 | 500 | +50 |
| 11th year | 450 | 500 | +50 |
| Each year thereafter | 450 | 500 | +50 |
But if the rate of interest were 4½ per cent, the comparison would be different. The present value of the sacrifices or costs would be $1016, and the present value of the gains or returns $932, showing a preponderance of the sacrifices or costs. That is, if the rate of interest is 4½ per cent, the cost from using the land for forestry rather than farming outweighs the returns. Therefore, when money is at 4½ per cent, the land would not be used for forestry purposes.
The general principle is, therefore, that among the various options open to the capitalist he chooses the most advantageous, or more fully expressed, the one which, compared with any other, offers advantages which in present value at the given rate of interest outweigh the disadvantages. But this is evidently merely another formulation of the original principle that the use chosen will be the one which has the maximum present value at the given rate of interest.
We may summarize the method of comparative advantage as follows: We are constantly confronted with the opportunity to choose one income stream rather than another. We inquire
what difference it makes whether one or the other alternative is chosen. We find often it makes two kinds of differences, advantages and disadvantages. If we start with the option which has the more immediate advantages and ask whether it is or is not worth while to give up this option and adopt the other instead, we may call the proposal so to do an
opportunity to invest, i.e., to incur certain disadvantages or, as they will hereafter be called,
costs, for the sake of certain advantages or, as they will hereafter be called,
returns.And we decide whether or not this investment opportunity is worth while by weighing the costs against the returns in terms of present worth, as reckoned by the rate of interest.
§3. The Concept of Rate of Return Over Cost
When we compare two optional income streams, and either may be preferable to the other according as one rate of interest or another obtains, the two options would stand on a par if the right intermediate rate were used for calculating the present values of the two options. That is, this equalizing rate is such that the present values of the two options would be equal, or what amounts to the same thing, it is such that, if that rate is used for discounting, the present value of the cost of choosing one option instead of the other would be equal to the present value of the return.
This hypothetical rate of interest which if used in calculating the present worth of the two options compared would equalize them or their differences (cost and return) may be called the
rate of return over cost and hereafter this name will generally be employed. This new magnitude (or factor) in our study plays the central rôle on the investment opportunity side of interest theory.
Let us now apply this rate of return over cost to the case of the options already used for illustration.
We have seen that, in our land example, if the rate of interest is 4 per cent, the net advantage is in favor of the forestry use, and if the rate of interest is 4½ per cent, the net advantage is in favor of the farming use. It is evident then that at some intermediate rate of interest the comparative advantages of the two uses would be exactly equal. This intermediate rate is approximately 4.2 per cent,
and this equalizing rate is the rate of return over cost.
But we may reduce the comparison to its simplest form if we change the figures in the example to the following:
| TABLE 7 Farming and Forestry Use Compared in Terms of Rate of Return Over Cost |
|||
|---|---|---|---|
| Net Value of Farming Use
|
Net Value of Forestry Use
|
Net Difference in Favor of Forestry Use
|
|
| 1st year | $100 | $000 | -$100 |
| 2nd year | 100 | 210 | +110 |
| 3rd year | 100 | 100 | 000 |
| 4th year | 100 | 100 | 000 |
| Each subsequent year | 100 | 100 | 000 |
In this case the equalizing rate, or the rate of return over cost, is evidently 10 per cent. At the cost of $100 there is a return of $110, or 10 per cent over the $100. At 10 per cent the present worth of the two will be equal; for the present worth of the return $110 due next year is, reckoning at 10 per cent, exactly $100 and the present value of the cost, $100, due immediately, is also $100.
The example just given, in which the cost ($100) is only one item and the return ($110) is also only one item received one year later, is the simplest possible example. But the same principle holds true however complicated may be the series of items constituting the costs and returns.
Perhaps the next simplest example is that in which one option shows in the present year a cost (of, say, $100) compared with the other but shows a return (of, say, $8) for
every future year in perpetuity. Under these circumstances the equalizing rate (or the rate of return over cost) is 8 per cent.
Thus the expression “rate of return over cost” is applied to the comparative merits of two alternative income streams. I repeat that by
cost is meant the
comparative loss from one’s income stream at first, caused by substituting one use of capital for another, and by
return is meant the
comparative gain which accrues usually later, by reason of this same substitution. The
cost is literally the difference it makes today and the
return is the
difference it makes in the future—the first negative, the second positive.
It will be noted that this description is all inclusive. It applies to every possible cost and every possible return. The problem of the investor—and everyone is an investor in some degree and manner—is always to answer the question: “What
difference does it make to my income stream whether I choose one way rather than another? What do I sacrifice and what do I gain?” If the cost comes first and the return comes later, he wants to know if the return exceeds the cost by enough to be worth while. The excess is his return over cost and the important magnitude is the rate per annum of this return over cost.
Usually this question, “What difference does it make?”, is asked with reference to a proposed change from an old to a new layout of one’s plans. Will a little more tilling of the soil bring a big or a little return, both the tilling and return in crops being translated at their market prices into money? Will a new harvesting machine at market prices make enough difference in the harvest to be worth while? Will a merger of two companies make a return in future profits sufficient to make the temporary costs involved in the merging process worth while? It will be seen, then, that the concept here used of investment
opportunity is not contrary to ordinary ideas. It includes them. Every time a person considers what he calls an opportunity to invest, he weighs in his mind the differences in his expected income—the expected future additions against the more immediate subtractions. Even when the investment is not made in installments out of savings from current income, but is made in one lump sum, it must not be forgotten that this lump sum invested merely represents the sacrifice of some alternative income stream.
The rate of return over cost is not, of course, to be confused with the rate of interest which it helps to determine, any more than the rate of impatience is to be so confused.
§4. The Principle of Return over Cost
Now let us restate the forestry-farming-mining comparison in the land example of the preceding chapter in terms of the rate of return over cost.
If the actual market rate of interest is 4 per cent, a person using the land for farming, or thinking of so doing, would find forestry preferable. The change from farming to forestry would cost certain sacrifices of income in the first four years, as specified in Table 6, but would return certain net additions thereafter. The rate of return over cost which would be realized by choosing the forestry rather than the farming use is 4.2 per cent. He would be realizing 4.2 per cent, which is more than the market rate, 4 per cent.
If, however, the market rate of interest were 4.5 per cent, it would not pay to change from farming to forestry; for to do so would return only 4.2 per cent as compared with 4.5 per cent which he could get in the loan market.
Our farmer would prefer to invest at 4.5 per cent
by lending in the first four years $450, $450, $150, $50 rather than sacrifice these same amounts for 4.2 per cent by giving up farming for forestry. To induce him to make a change, the
rate of return over cost must exceed the rate of interest.*62
Thus, by employing the concept of a rate of return over cost, we may restate the investment opportunity principle of maximum present value, or the principle of comparative advantage, as the principle of greatest return over cost. So stated the principle is:
Out of all possible options open to a person that particular one is selected, the comparison of which with any other option affords a rate of return over cost equal to or greater than the rate of interest.
§5. Marginal Rate of Return Over Cost
Next let us apply this statement of principle to the case in which the range of choice is not confined to a
few definite options, but extends to an
infinite number varying by continuous gradations. This case is really more like the facts of life than the imaginary case of a few fixed options, such as the farming, mining, or forestry uses of land. In fact, each of these three uses is in actual
life not merely a single use, as was assumed for simplicity, but a whole group of optional uses. Thus, the farmer may carry farming to any degree of intensity, and the same may be said of mining or lumbering. For each particular degree of intensity he will have a different income stream. He may, for instance, find it possible at the beginning of the scale of intensity to invest an extra $100 worth of his or other labor in the present in order that one year later he may have an income of $150 more than he would otherwise have. If the rate of interest is 4 per cent per annum, he would evidently prefer this course, for while his present income is diminished by $100 he would realize an increase of $150 in his income one year later, or $50 over cost, making a rate of return over cost of 50 per cent per annum, whereas the interest is only 4 per cent. If he invests another $100 in present cultivation, this will add to his income in a year’s time something less than the $150, say $130, making a rate of return of 30 per cent. And so each successive choice compared with its predecessor follows the
law of decreasing returns. A third $100 will add, let us say, $120 or $20 more than the cost. A fourth $100 may secure a return of an additional $10 a year over and above the cost; a fifth $100 may secure a return of an additional $8; a sixth $100 may bring $6; a seventh $100, $4.
Thus far, in the scale of intensity, each option yields 4 per cent or more, while the rate of interest is 4 per cent a year. The lure of a rate of return equal to or in excess of the interest rate will induce the farmer to incur the additional cost. But the next option, let us say, is to invest an eighth $100 for an additional $3 a year. Evidently, it will not be to the farmer’s advantage to take this last step; he will stop at the previous step, at which
he barely gets a 4 per cent return. As we saw in the preceding section, each successive investment opportunity is chosen as long as the rate of return over cost of that option compared with the previous one is greater than the rate of interest, and that use is rejected at which the rate of return over cost becomes less than the rate of interest. The intensiveness of his farming is thus determined by the rate of interest. In our example, he will stop at the seventh $100 which barely returns the equivalent of the rate of interest. We may say, then, that he chooses that degree of intensiveness at which the rate of return over cost is barely more than the rate of interest. This envisages a series of possible income streams arranged successively in order of intensiveness of the cultivation required for each. By substituting successively one of these income streams for the preceding we incur more cost but obtain more return. The rate of the return over the cost compared with the market rate of interest is our guide as to how far to go in the series. We thus reach the
marginal rate of return over cost.
§6. The Illustration of Cutting a Forest
To vary the illustration from intensive agriculture to forestry, let us apply the option selection idea to cutting a forest. Let us consider as the first option the cutting of the forest at the end of nine years, when the income stream consists of the single-item, the production of 900 cords of wood (or $900 if wood is $1 a cord).
*63
The second option is holding the forest for another
year of growth and cutting it at the end of ten years, to receive an income item of 1000 cords (or $1000, assuming an unchanging price of $1 a cord). The two alternatives may be put in precisely the same tabular form as the one previously employed for the case of forestry and farming as follows:
| TABLE 8 Optional Incomes from Forest |
|||
|---|---|---|---|
| 10-Year Plan
|
9-Year Plan
|
Difference in Favor of 10-Year Plan |
|
| 1st year | $000 | $000 | |
| 2nd year | 000 | 000 | |
| ……… | … | … | |
| 9th year | 000 | 900 | -900 |
| 10th year | 1000 | 000 | +1000 |
The last column shows that the ten-year plan, compared with the nine-year plan, involves a cost of 900 in the ninth year, but involves a return of 1000 in the tenth year. The rate of the return (100) over the cost (900) would thus be a little over 11 per cent. If the rate of interest in the market is 5 per cent, it would evidently pay to wait, that is, to postpone the cutting to the tenth year.
The next option would be to cut in the eleventh year, which, as compared with the previous or ten-year plan, would, let us say, cost 1000 in the tenth year and return 1050 in the eleventh year—in other words, give a rate of return over cost of 5 per cent. Evidently, then, it would be a matter of indifference whether the forest were cut in the tenth or eleventh year, inasmuch as the rate of return over cost would be exactly equal to the rate of interest.
Similar reasoning might show that the choice of the next option, that of cutting the forest in the twelfth year,
would yield a return of say 21 / 1050 or 2 per cent. Inasmuch as 2 per cent is less than the rate of interest, this alternative would be rejected. Thus, equilibrium is found where the rate of return on cost equals 5 per cent, the rate of interest.
The case may be illustrated by Chart 16. Let
AB represent the number of cords of wood on an acre of growing trees; let
A‘
B‘ represent the amount of wood which may be expected at the end of five years; let
A”
B” represent what may be expected in ten years and so on for successive years until the forest reaches its maximum growth,
MN, at the end of
AM years. The percentage-slope, or rate of ascent,
*64 of the curve
BN at any point, therefore,
represents the rate of growth, at any time, of the forest. The value at present (at the point of time
A) of the forest,
in terms of cords of wood, will be represented, not by the height
AB, but in a different manner, as follows: If from
B‘ the discount curve
*65B‘
C‘ be drawn, the ordinate of which, at any time, will represent the discounted values of
A‘
B‘ at that time, then
AC‘ will represent the present value of
A‘
B‘, i.e., of the amount of the wood if cut in five years. Similarly,
AC” will represent the present value of
A”
B”, the wood if cut in ten years. We draw in like manner a number of discount curves until one is found,
tT, which is tangent to the curve
BN.At will then be the correct value of the young forest, and
D will represent the time at which it should be cut. Clearly,
At is quite different from
AB, the amount of wood at the present time, and also from
DT, the amount of wood at the time of cutting.
At is the maximum present value out of all possible choices as to the time of cutting. If the forest is for some reason to be cut at once, its value will be only
AB; if it is to be cut at
A‘ its present value will be
AC‘ if at
A”, it will be
AC”; if at
D, it will be
At.At is the maximum, for if the forest were cut at any other point of time on either side of
T the discount curve passing through that point would evidently lie below the curve
tT.
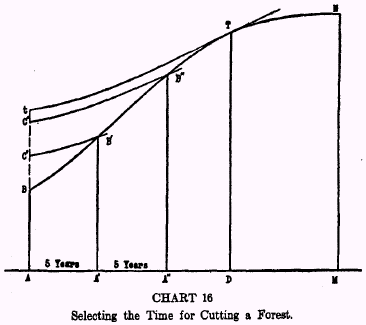
At the time
A, then, the wood in the forest is only
AB but, assuming proper foresting, the value of the forest in terms of wood is
At; the rate of growth of the forest is the percentage-slope of
BN at
B, but the rate of interest is the percentage-slope (the same at all points) of
tT.
At the point of tangency alone, namely
T, are the rate of growth and rate of interest (both in terms of wood)
identical, and to that extent at least there is truth in the thesis that the rate of interest is the rate of growth. This, however, is not the average rate of growth but the rate of growth at the time of cutting. This is the element of truth in the organic productivity theory of Henry George and Alexander Del Mar. These writers based their theories of interest on the productivity of those particular kinds of capital which reproduce themselves, and reached the conclusion that, in the last analysis, the rate of interest consists in the “average rate of growth of animals and plants.”
*66.
Evidently the theory would be substantially correct if “average” were replaced by “marginal.” The example of cutting the forest illustrates the simplest theoretical case of marginal productivity as a true basis of the rate of interest.
But that this element of truth is insufficient of itself to afford a complete determination of the rate of interest is evident when we consider that the point at which the forest is to be cut itself depends, among other causes, upon the rate of interest! If the interest rate rises, the discount curves employed become steeper and the point of tangency
T moves toward the left, that is, the forest will be cut earlier.
In no case, of course, is the time of cutting the time of maximum stumpage. To wait for that time would eat up too much interest. The theories of Del Mar and Henry George thus constitute a special case under the opportunity principles.
§7. Other Similar Illustrations
Both the preceding examples, one of intensive agriculture and the other of forest cutting, involve (1) an immediate cost and (2) a return one year later, thus reducing the marginal rate of return over cost to such simple calculations as (105 – 100) ÷ 100 = 5 per cent.
We may vary the illustration indefinitely and still preserve this elementary simplicity. A merchant has always before him an indefinite number of possible income-streams from which to choose. As in the case of the land cultivation and the forest cutting we may simplify his choice by supposing successive doses of costs of $100, each spent on more or better machinery, more or better workmen, more or better advertising, more or better supervision, and so forth, each $100 cost being immediate, and then supposing the returns to these successive doses of invested cost to come respectively one year later and to be respectively, say, $140, $130, $115, $106, $105, $104; so that the excess of return over the cost will be respectively $40, $30, $15, $6, $5, $4. Thus the rate of return over cost will be respectively 40, 30, 15, 6, 5, and 4 per cent. The enterpriser will incur the costs as long as the rate of return over these costs is greater than the market rate of interest. In this case, therefore, he will stop at 5 per cent if the market rate of interest is 5 per cent. Again we have ($105 – $100) ÷ $100 = 5 per cent.
In practice, however, we seldom, if ever, have such simplicity in calculating the rate of return over cost and there are innumerable other types of contrast between the successive income streams which may be at the same time under consideration by the investor.
§8. The Case of Perpetual Returns
Next in simplicity is the type in which $100 of immediate cost is incurred for the sake of a perpetual annuity of $5 a year. Let us suppose the individual possesses some swamp land in a primitive condition. He has a large range of choice as to the method of utilizing this land. He wants to make the most of his opportunities. One option is to allow the land to remain a swamp. Others occur if, by clearing and draining it, it is converted into crop-yielding land, the yield varying with the thoroughness with which the clearing and draining are accomplished. Let us suppose that, under the first option, he derives a perpetual net income of $50 a year, and let us suppose that, at an immediate cost of $100 in his labor or in payment for the labor of others for clearing and draining, he can secure an addition of $25 a year. That is, as between retaining these two options, the swamp undrained and draining it partially, the latter involves a $100 decrease of immediate income and thereafter an income of $75 a year, or an increase of $25 a year. In other words, at the cost of $100 he will obtain a return of 25 per cent per annum in perpetuity.
Evidently, if the rate of interest in the market is 5 per cent, or anything less than 25 per cent, it will pay him to make such an investment, borrowing at 5 per cent if he wishes the $100 required for the improvement. Next suppose that another $100 invested in improving the swamp would yield crop returns of $90, or $15 more than before. The investment of this second $100 yields 15 per cent, and is therefore also a lucrative one, when the rate of interest is only 5 per cent. A third $100 may increase the annual crop still further, say by $10, netting
a return of 10 per cent over the cost. A fourth $100 invested will cause the annual crop to be increased by $5 giving a return of 5 per cent. A fifth $100 will cause the crop to increase by $3—a return of 3 per cent. Evidently it will pay the farmer to invest in draining and improving his swamp up to the fourth $100, but not to the fifth $100. Rather than invest this fifth $100 and receive thereon an annual income of $3 a year, he would prefer to invest $100 in the savings bank and receive 5 per cent a year.
In other words, the exact degree of intensity with which he will improve and cultivate his land is determined by the current rate of interest. Should the rate of interest in the market fall from the 5 per cent just assumed to 2 per cent, it would then pay him to invest the fifth $100. For, evidently, if need be, he could borrow $100 at 2 per cent and receive from his land a return of 3 per cent. As Rae has so clearly pointed out, in communities where the rate of interest is low, swamps will be more thoroughly improved, roads better made, dwellings more durably built, and all instruments developed to a higher degree of efficiency so as to yield a lower marginal return over cost than in a community where the rate of interest is high.
§9. The General Case
In general, the rate of return over cost has to be derived by more complicated methods. As already indicated, the rate of return over cost is always that rate which, employed in computing the present worth of all the costs and the present worth of all the returns, will make these two equal. Or, as a mathematician would prefer to put it, the rate which, employed in computing the present worth
of the whole series of differences between the two income streams (some differences being positive and others negative) will make the total zero.
If the rate, so computed, were taken for every possible pair of income streams compared as to their advantages and disadvantages, it would authentically decide in each case which of the pair is to be preferred. That one which compared with the other shows a rate of return on sacrifice greater than the rate of interest would be preferred and the other rejected. By such preferences and rejections the individual would be led to a final
margin of choice of the best option. This contrasted with its nearest rival would show a marginal rate of return over cost equal to the market rate of interest.
The problems of choosing when to cut a forest, of what length to make a production period, how far to push any industrial policy, to what degree of intensiveness to cultivate land, are all the same problem of choosing the best out of innumerable possible income streams, i.e.,
problems of making the best out of one’s investment opportunities.
In each problem the rival income streams present differences as to size and shape. They can best be compared by means of diagrams. Charts 17 to 20 show typical ways in which the income streams may conceivably be subjected to slight variation. The unbroken line in each case indicates the income stream chosen, and the dotted line the next best opportunity, rejected on behalf of the unbroken line. Chart 17 may be taken as applying to the planting of a crop; Chart 18 to the draining of a swamp; Chart 19 to the cutting of a forest; and Chart 20 to the case of alternating costs and returns.

§10. Range of Choice Depends on Interest Rate
Up to this point one complication in the problem of interest has been kept in the background. Although this complication does not invalidate any of the principles
which have been developed, it seemed advisable not to distract attention from the essential features of the theory by introducing it prematurely. The complication referred to is, after all, more intricate than important. It consists in the fact that not only, as we have seen, does the choice between different optional income streams depend upon the rate of interest, but also that even the
range of choice depends upon that rate. If the rate of interest is changed, a change is produced not only in the present values of the income items but in the income items themselves.
The net income from any instrument or group of instruments of wealth is the difference between the total gross income and the outgo. But many of the elements, both of income and outgo, are materially dependent upon the rate of interest. This is especially true of those items of income and outgo which are not final but merely intermediate or interactions.
*67 In the case of interactions, a change in the rate of interest affects the income stream directly, because, as has been shown elsewhere,
*68 the valuation of an interaction (i.e., intermediate service) involves the discount process and is therefore dependent upon the rate of interest. Thus, the iron yielded by an iron mine has its value determined in part by the discounted value of the machinery to be made of it and therefore its value will be affected by a change in the rate by which this discount is reckoned.
For present purposes, it is only necessary to emphasize the bare fact that the
range of choice between different income streams is somewhat dependent upon the rate of interest. If the modification due to this fact were introduced
into the tables previously given for the three different uses of land, we should find that the income streams from using the land for farming, forestry, and mining would differ according to the rate of interest.
Thus, let us suppose, as before in Chapter VI, §2, that for a rate of interest of 5 per cent the three optional income streams are:
| TABLE 9 The Original Optional Income Streams of Farming, Forestry, and Mining |
|||
|---|---|---|---|
| Farming
|
Forestry
|
Mining
|
|
| 1st year | $450 | $000 | $2000 |
| 2nd year | 450 | 000 | 1800 |
| 3rd year | 450 | 300 | 1600 |
| 4th year | 450 | 400 | 1400 |
| 5th year | 450 | 500 | 1200 |
| 6th year | 450 | 500 | 1000 |
| 7th year | 450 | 500 | 800 |
| 8th year | 450 | 500 | 600 |
| 9th year | 450 | 500 | 400 |
| 10th year | 450 | 500 | 200 |
| Thereafter | 450 | 500 | 000 |
In our previous discussion, when we changed the rate of interest from the 5 per cent of the foregoing table to 4 per cent, we supposed the items in the foregoing table to remain unchanged. The only change we had then to deal with was the change in their present values. Now, however, we admit the possibility of a change in the table items themselves. If the rate of interest falls to 4 per cent, the product of forest, farm, and mine will be more nearly equal to the value of the ultimate services to which they lead. The value of lumber will be more nearly equal to the value of the houses it makes, and these to the value of the shelter they give; the value of wheat from a farm will be nearer the value of the bread it will make; and the value of ore from a mine will be
nearer the value of the steel it will become, and this, in turn, more nearly equal to the values of those innumerable satisfactions which come about through the use of steel. These shiftings forward of the values of the intermediate income of forest, farm and mine toward the values of the ultimate satisfactions to which they lead, combined with possible readjustments in the values of these satisfactions themselves—the values of house shelter, bread consumption, etc.—will result in a change, say, in the items in the foregoing table, where we were assuming a 5 per cent rate of interest, to the following table wherein the rate is 4 per cent.
| TABLE 10 The Optional Income Streams of Farming, Forestry, and Mining, as Affected by the Rate of Interest |
|||
|---|---|---|---|
| Farming
|
Forestry
|
Mining
|
|
| 1st year | $500 | $000 | $2100 |
| 2nd year | 500 | 000 | 1900 |
| 3rd year | 500 | 350 | 1700 |
| 4th year | 500 | 450 | 1500 |
| 5th year | 500 | 600 | 1300 |
| 6th year | 500 | 600 | 1100 |
| 7th year | 500 | 600 | 850 |
| 8th year | 500 | 600 | 650 |
| 9th year | 500 | 600 | 450 |
| 10th year | 500 | 600 | 225 |
| Thereafter | 500 | 600 | 000 |
If, then, the rate is 5 per cent, the land owner will make the most of his opportunities by choosing that use among the three which, computing from the figures in the
first table, has the greatest present value; while if the rate is 4 per cent, he will choose that which, computing from the figures in the
second table, has the greatest present value. If, then, the rate is 5 per cent, he will choose mining, since, as we saw in Chapter VI, §4, the present values, when we compute at 5 per cent, are: forestry, $8820;
farming, $9000; mining, $9110; but if the rate is 4 per cent, he will choose the highest from the present values at 4 per cent, computed from the second table. These present values now are: forestry, $13,520; farming, $12,500; mining, $10,100.
Whatever the final outcome of all the readjustments, it is evident that the introduction of the influence of the rate of interest on the range of choice does not in any material way affect the reasoning already given in regard to the determination of the rate of interest. Since the rate of interest will itself fix the range of choice, it will still be true that, once the range of choice is fixed for a given rate of interest, the individual will choose, as before, that use which has the maximum present value. On the basis of this choice he is then led to borrow or lend in order to modify his income stream so that his degree of impatience may harmonize with the rate of interest. If, upon an assumed rate of interest, the borrowing and lending for different individuals actually cancel one another—in other words, clear the market—then the rate of interest assumed is clearly the one which solves the problem of interest; otherwise the borrowing and lending will not be in equilibrium, and some other rate of interest must be selected. By successively postulating different rates of interest, and remembering that each rate carries with it its own range of options and its own set of present values of those options, we finally obtain that rate which will clear the market.
The rate which will clear the market, while drawing into equality with itself all marginal impatience rates and all marginal rates of return on cost, is the one which solves the problem of interest under the assumed conditions.
§11.
The Investment Opportunity Principles Summarized
The chief results of the chain of reasoning which has been followed in this chapter are that the same principle of investment opportunity may now be stated in four ways as:
The Principle of Maximum Present Value.
Out of all options, that one is selected which has the maximum present value reckoned at the market rate of interest.
The Principle of Comparative Advantage.
Out of all options, that one is selected the advantages of which over any other option outweighs its disadvantages, when both these advantages and disadvantages—returns and costs—are discounted at the market rate of interest.
The Principle of Return over Cost.
Out of all options, that one is selected which, in comparison with any other, yields a rate of return over cost equal to or greater than the market rate of interest.
The Same Principle when the Options Differ by Continuous Gradations.
Out of all options, that one is selected the differences of which from its nearest rival gives a rate of return over cost equal to the market rate of interest. Such a rate is called the
marginal rate of return on cost.
In whichever of these aspects it is regarded, this is the principle of investment opportunity. However he reckons it, every one measures his opportunities to invest—to
modify his income stream—in reference to the rate of interest by applying this principle.
We can scarcely exaggerate the importance of the concept of “rate of return over cost” and of its special variety ”
marginal rate of return over cost” as an element in our analysis of the conditions determining the rate of interest. It supplies, on the physical or technical or productivity side of the analysis, what the marginal rate of time preference supplies on the psychical side. The subject is, as has been seen, one which may be looked upon from many points of view, which may seem at first to be inconsistent yet which may be thoroughly coordinated under the foregoing generalizations.
§12. Interrelation of Human Impatience and Investment Opportunity
The rate of interest, then, is the resultant of three sets of principles of which the market principles are self-evident. The other two great sets of principles are the one comprising two principles of human impatience and the other comprising two principles of investment opportunity. The principles of impatience relate to subjective facts; those of investment opportunity, to objective facts. Our inner impatience urges us to hasten the coming of future income—to shift it toward the present. If incomes could be shifted at will, without shrinking in the process, they would be shifted much more than they are. But technical limitations prevent free shifting by penalizing haste and rewarding waiting. Thus Henry Ford might have continued making his Model T car. He would have thereby enjoyed a large immediate income but a gradually decreasing one. Instead, he resolved to place a better type of car on the market. To do so, he had to suspend
the productive operations of his plant for a year, to scrap much of his old machinery and to provide a new installation at the cost of millions. The larger returns which he expected from the sale of the new car were only obtainable by the sacrifice of immediate income—by waiting.
Our outer opportunities urge us to postpone present income—to shift it toward the future, because it will expand in the process. Impatience is impatience to spend, while opportunity is opportunity to invest. The more we invest and postpone our gratification, the lower the investment opportunity rate becomes, but the greater the impatience rate; the more we spend and hasten our gratification, the lower the impatience rate becomes but the higher the opportunity rate.
If the pendulum swings too far toward the investment extreme and away from the spending extreme, it is brought back by the strengthening of impatience and the weakening of investment opportunity. Impatience is strengthened by growing wants, and opportunity is weakened because of the diminishing returns. If the pendulum swings too far toward the spending extreme and away from the investment extreme it is brought back by the weakening of impatience and the strengthening of opportunity for reasons opposite to those stated above.
Between these two extremes lies the equilibrium point which clears the market, and clears it at a rate of interest registering (in a perfect market) all impatience rates and all opportunity rates.
It is all a question of the
time and amount of the series of items constituting real income. Shall we get income enjoyment now or later and how much? Shall we spend or invest?
less than the rate of interest. In such a case it would be more convenient, in comparing the two options, to regard them in the reverse order, that is, to consider the advantages of the farming use over the mining use, so that the disadvantages may come first, i.e., the investment precede the returns. As long as the costs always precede the returns, we need only to consider whether or not the rate of return over cost exceeds the rate of interest.
Science of Money. New York, Macmillan & Co., 1896; George, Henry.
Progress and Poverty. New York, Sterling Publishing Co., 1879. For a general criticism of this theory see Lowry,
The Basis of Interest, American Academy of Political and Social Science, March, 1893, pp. 53-76
The Nature of Capital and Income, Chapters VII, VIII, IX, and X.
Part II, Chapter 8
