The Theory of Interest
By Irving Fisher
THE tremendous expansion of credit during and since the World War to finance military operations as well as post-war reparations, reconstruction, and the rebuilding of industry and trade has brought the problems of capitalism and the nature and origin of interest home afresh to the minds of business men as well as to economists. This book is addressed, therefore, to financial and industrial leaders, as well as to professors and students of economics.Inflation during and since the War caused prices to soar and real interest rates to sag in Germany and other nations far below zero thus impoverishing millions of investors. In all countries gilt-edge securities with fixed return became highly speculative, because of the effect of monetary fluctuations on real interest rates. After the War the impatience of whole peoples to anticipate future income by borrowing to spend, coupled with the opportunity to get large returns from investments, raised interest rates and kept them high. Increased national income has made the United States a lender nation. At home, real incomes have grown amazingly because of the new scientific, industrial, and agricultural revolutions. Interest rates have declined somewhat since 1920, but are still high because the returns upon investments remain high. Impatience to spend has been exemplified by the organization of consumers’ credit in the form of finance companies specially organized to accommodate and stimulate installment selling and to standardize and stabilize consumption…. [From the Preface]
First Pub. Date
1930
Publisher
New York: The Macmillan Co.
Pub. Date
1930
Comments
1st edition.
Copyright
The text of this edition is in the public domain.
- Dedication
- Errata
- Preface
- Suggestions to Readers
- Part I, Chapter 1
- Part I, Chapter 2
- Part I, Chapter 3
- Part II, Chapter 4
- Part II, Chapter 5
- Part II, Chapter 6
- Part II, Chapter 7
- Part II, Chapter 8
- Part II, Chapter 9
- Part III, Chapter 10
- Part III, Chapter 11
- Part III, Chapter 12
- Part III, Chapter 13
- Part III, Chapter 14
- Part IV, Chapter 15
- Part IV, Chapter 16
- Part IV, Chapter 17
- Part IV, Chapter 18
- Part IV, Chapter 19
- Part IV, Chapter 20
- Part IV, Chapter 21
- Appendix to Chapter I
- Appendix to Chapter X
- Appendix to Chapter XII
- Appendix to Chapter XIII
- Appendix to Chapter XIX
- Appendix to Chapter XX
- Appendix to Chapter XX
§1. Price Changes and Interest Rates
PART IV, CHAPTER XIX
THE RELATION OF INTEREST TO MONEY AND PRICES
No problem in economics has been more hotly debated than that of the various relations of price levels to interest rates. These problems are of such vital importance that I have gone to much trouble and expense to have such data as could be found compiled, compared, and analyzed. The principal result of these comparisons are given in this chapter.
The general theory of the relationship between the rate of interest and the buying power of money was summarized in Chapter II. The main object of this chapter is to ascertain to what extent, if at all, a change in the general price level actually affects the market rates of interest.
Since the theory of Chapter II presupposes foresight, the question arises at the outset: How is it possible for a borrower or lender to foresee variations in the general price level with the resultant increase or decrease in the buying power of his money? A change in the value of money is hard to determine. Few business men have any clear ideas about it. If we ask a merchant whether or not he takes account of appreciation or depreciation of money values, he will say he never heard of it, that “a dollar is a dollar!” In his mind, other things may change in terms of money, but money itself does not change. Most people
are subject to what may be called “the money illusion,” and think instinctively of money as constant and incapable of appreciation or depreciation. Yet it may be true that they do take account, to some extent at least, even if unconsciously, of a change in the buying power of money, under guise of a change in the level of prices in general. If the price level falls in such a way that they may expect for themselves a shrinking margin of profit, they will be cautious about borrowing unless interest falls, and this very unwillingness to borrow, lessening the demand in the money market, will tend to bring interest down. On the other hand, if inflation is going on, they will scent rising prices ahead and so rising money profits, and will be stimulated to borrow unless the rate of interest rises enough to discourage them, and their willingness to borrow will itself tend to raise interest.
And today especially, foresight is clearer and more prevalent than ever before. The business man makes a definite effort to look ahead not only as to his own particular business but as to general business conditions, including the trend of prices.
Evidence that an expected change in the price level does have an effect on the money rate of interest may be obtained from several sources. During the free-silver agitation of 1895 and 1896, municipalities could sell gold bonds on better terms than currency bonds. There was a strong desire on the part of lenders to insert a gold clause in their contracts, and to secure it they were willing to yield something in the interest rate.
The same tendency was strikingly shown in California during the inflation period of the Civil War.
*43 For a time,
gold contracts could not be enforced, and in consequence interest rates were exceptionally high.
§2. United States Coin and Currency Bonds
A more definite test may be made where two standards are simultaneously used. An excellent case of this kind is supplied by comparing two kinds of United States bonds, one payable in coin and the other in currency. From the prices for which these bonds sold in the market it is possible to calculate the interest realized by the investor. The currency bonds were known as currency sixes and matured in 1898 and 1899. The coin bonds selected for comparison were the fours of 1907. The table on page 402 gives the rates of interest realized in the two standards, together with the premium on gold.
Several points in this table deserve notice. In 1870 the investor realized 6.4 per cent in terms of gold but was willing to accept a return of only 5.4 per cent currency. Why should a gold bond be thus inferior to a paper bond? This has become intelligible in the light of the theory which was explained in Chapter II. It meant the hope of resumption. Just because paper was depreciated below gold and there was a chance of bringing it up to par, there was in prospect a great rise in its value, as compared with gold. It was not until 1878, just before resumption, when the prospect of any further rise disappeared, that the relative position of the two rates of interest was reversed. After resumption in 1879, when paper money did reach par with gold, the two bond rates remained very nearly equal for several years, until fears of inflation from Greenbackism and Free-Silverism again produced a divergence. The quotations for 1894, 1895, and 1896 showed a considerably higher rate of interest
in the currency standard than in the coin standard, as well as a higher rate in both standards than in previous years. The contrast is that between 2.7 per cent and 3.5 per cent in 1894, and between 3.2 per cent and 4.3 per cent in 1896. The divergence of the two rates is explainable
as the effect of the fear of Bryan’s free-silver proposal, incorporated (July, 1896) in the platform of the Democratic party. Had free coinage of silver been restored at the ratio of 16 to 1, since the bondholders had the option of demanding either gold or silver in payment, coin bonds presumably would still have meant gold bonds. Hence investors were ready to accept lower interest on these bonds than on currency bonds.
| TABLE 11 Rates of Interest Realized from Dates Named to Maturity*44 |
||||||
|---|---|---|---|---|---|---|
|
|
||||||
| Coin
|
Currency
|
Price of Gold *45 |
Coin
|
Currency
|
||
| Jan. 1870 | 6.4 | 5.4 | 119.9 | Jan. 1879 | 3.7 | 4.5 |
| July 1870 | 5.8 | 5.1 | 112.2 | Jan. 1880 | 3.8 | 4.0 |
| Jan. 1871 | 6.0 | 5.3 | 110.8 | Jan. 1881 | 3.3 | 3.4 |
| July 1871 | 5.8 | 5.0 | 113.2 | Jan. 1882 | 3.0 | 3.5 |
| Jan. 1872 | 5.3 | 4.9 | 109.5 | Jan. 1883 | 2.9 | 3.3 |
| July 1872 | 5.6 | 5.0 | 113.9 | Jan. 1884 | 2.6 | 2.9 |
| Jan. 1873 | 5.7 | 5.1 | 111.9 | May 1885 | 2.7 | 2.7 |
| July 1873 | 5.4 | 5.0 | 115.3 | Jan. 1886 | 2.6 | 2.6 |
| Jan. 1874 | 5.0 | 5.0 | 110.3 | Jan. 1887 | 2.3 | 2.6 |
| July 1874 | 5.1 | 4.9 | 110.7 | Mar. 1888 | 2.3 | 2.9 |
| Jan. 1875 | 5.0 | 4.7 | 112.6 | Jan. 1889 | 2.2 | 2.6 |
| July 1875 | 5.1 | 4.4 | 117.0 | May 1890 | 2.1 | 2.6 |
| Jan. 1876 | 4.7 | 4.4 | 112.9 | July 1891 | 2.4 | 3.0 |
| July 1876 | 4.5 | 4.2 | 112.3 | Jan. 1892 | 2.6 | 3.1 |
| Jan. 1877 | 4.5 | 4.4 | 107.0 | Mar. 1893 | 2.8 | 3.1 |
| July 1877 | 4.4 | 4.3 | 105.4 | Nov. 1894 | 2.7 | 3.5 |
| Jan. 1878 | 5.0 | 4.6 | 102.8 | Aug. 1895 | 2.8 | 3.6 |
| July 1878 | 3.9 | 4.4 | 100.7 | Aug. 1896 | 3.2 | 4.3 |
§3. Gold and Rupee Bonds
Having compared the rates of interest of paper and coin bonds, we may next compare those of gold and silver securities. The comparison, to be of value, must be between gold and silver contracts in the same market and with the same security. Fortunately such contracts have been available in the London market of government securities. The loans of India have been made partly in gold and partly in silver, and both forms of securities have been quoted in London.
*46 The interest on the silver bonds, or rather rupee bonds, was paid by draft on India. The sums actually received in English money depended on the state of the exchanges. The rate of interest in the silver standard was calculated
*47 in the same way as was
shown for coin bonds in §2. The results follow:
| TABLE 12 Rates of Interest Realized from Dates Named to Maturity or in Perpetuity *48 |
||||
|---|---|---|---|---|
|
|
||||
| Rupee *49 |
Gold *50 |
Difference
|
Exchange on India
|
|
| Pence per Rupee | ||||
| 1865 | 4.3 | 4.1 | .2 | 23.2 |
| 1868 | 4.3 | 4.0 | .3 | 23.0 |
| 1870 | 4.3 | 4.0 | .3 | 23.6 |
| 1871 | 4.1 | 3.8 | .3 | 23.2 |
| 1872 | 3.9 | 3.7 | .2 | 22.6 |
| 1873 | 3.9 | 3.7 | .2 | 22.4 |
| 1874 | 3.9 | 3.8 | .1 | 22.2 |
| 1875 | 4.0 | 3.6 | .4 | 21.9 |
| 1876 | 4.1 | 3.7 | .4 | 20.5 |
| 1877 | 4.1 | 3.7 | .4 | 20.9 |
| 1878 | 4.2 | 3.9 | .3 | 20.2 |
| 1879 | 4.4 | 3.7 | .7 | 19.7 |
| 1880 | 4.3 | 3.6 | .7 | 20.0 |
| 1881 | 4.0 | 3.4 | .6 | 19.9 |
| 1882 | 3.9 | 3.5 | .4 | 19.5 |
| 1883 | 4.1 | 3.4 | .7 | 19.5 |
| 1884 | 4.1 | 3.3 | .8 | 19.5 |
| 1885 | 4.1 | 3.5 | .6 | 18.5 |
| 1886 | 4.1 | 3.5 | .6 | 17.5 |
| 1887 | 4.1 | 3.4 | .7 | 17.2 |
| 1888 | 4.1 | 3.1 | 1.0 | 16.5 |
| 1889 | 4.1 | 3.0 | 1.1 | 16.5 |
| 1890 (1st half) | 4.0 | 3.0 | 1.0 | 17.6 |
| 1890 (2nd half) | 3.9 | 3.1 | .8 | 19.3 |
| 1891 | 3.8 | 3.1 | .7 | 17.1 |
| 1892 | 3.9 | 3.1 | .8 | 15.3 |
| 1893 | 3.9 | 3.0 | .9 | 15.0 |
| 1894 | 3.9 | 3.0 | .9 | 13.5 |
| 1895 | 3.4 | 2.8 | .6 | 13.4 |
| 1896 | 3.3 | 3.1 | .2 | 14.3 |
| 1897 | 3.5 | 3.1 | .4 | 15.1 |
| 1898 | 3.7 | 3.2 | .5 | 16.0 |
| 1899 | 3.6 | 3.2 | .4 | 16.1 |
| 1900 | 3.7 | 3.4 | .3 | 16.0 |
| 1901 | 3.7 | 3.5 | .2 | 16.0 |
| 1902 | 3.6 | 3.5 | .1 | 16.0 |
| 1903 | 3.5 | 3.5 | .0 | 16.0 |
| 1904 | 3.6 | 3.7 | -.1 | 16.1 |
| 1905 | 3.6 | 3.6 | .0 | 16.1 |
| 1906 | 3.6 | 3.2 | .4 | 16.0 |
Footnotes to the table are given on page 405.
From this table it will be seen that the rates realized to investors in bonds of the two standards differed but slightly until 1875, when the fall of Indian exchange began. The average difference from 1875 to 1892 inclusive was 0.7 per cent. Within this period, from 1884, exchange fell much more rapidly than before, and the difference in the two rates of interest rose accordingly, amounting in one year to 1.1 per cent. Inasmuch as the two bonds were issued by the same government, possessed the same degree of security, were quoted side by side in the same market, and were similar in all important respects except in the standard in which they are expressed, the results afford evidence that the fall of exchange (after it once began) was, to some extent, discounted in advance and affected the rates of interest in those standards. Of course investors did not form perfectly definite estimates of the future fall, but the fear
of a fall predominated in varying degrees over the hope of a rise.
The year 1890 was one of great disturbance in exchanges, the average for the first six months being 17.6 and for the last six months, 19.3. The gold price of the silver bonds rose from an average for the first six months of 73.8 to 83.5 for the last six months, but the rise in their silver price was only from 100.6 to 103.7, showing that the increase of confidence in the future of silver was not great, and, in fact, only reduced the disparity in the interest from 1.0 to .8 per cent.
This great rise in exchange and the slight revival in silver securities occurred simultaneously with the passage of the Sherman Act of July, 1890, by which the United States was to purchase four and a half million ounces of silver per month. The disturbance was doubtless due in some measure to the operation, or expected operation, of that law.
This is not the only case in which the relative prices of rupee paper and gold bonds were probably affected by political action. One of the smallest differences in the two rates occurs in 1878, which was the year of the Bland Act and of the first International Monetary Conference.
After the closure of the Indian mints to silver on June 26, 1893, exchange rose from 14.7 to 15.9, the gold price of rupee paper from 62 to 70, and consequently its rupee price from 101.2 to 105.7.
From this point the exchange again dropped, much to the mystification of those who had predicted an established parity between gold and silver at the new legal rate of 16d per rupee. There was much discussion as to the reasons for the failure of the legal rate to become operative. The chief reason seems to have been that the
closure of the mints to silver attracted into the circulation silver from other channels, especially old native hoards. Within a few years, however, this source of supply was dried up so that the legal par was reached in 1898 and was maintained thereafter, subject only to the slight variations of exchange due to the cost of shipping specie.
But until the par was proved actually stable by two or three years’ experience, the public refused to have confidence that gold and the rupee were once more to run parallel. Their lack of confidence was shown in the difference in the rates of interest in gold and rupee securities during the transition period, 1893-1898, and the two or three succeeding years. From 1893 to 1900 inclusive the two rates averaged .5 per cent apart. From 1901 to 1906 inclusive, the average difference was only .1 per cent,
*51 showing that confidence in the gold value of the rupee had been established.
§4. Money Interest and Real Interest
The foregoing comparisons relate to
simultaneous rates of interest in two contrasted monetary standards each actually used for loan contracts. We now turn to a comparison between money rates and real rates of interest, mentioned in Chapter II. Unfortunately no contracts in terms of real or commodity standards are available for quotation. All we can do is to note the changes in the
price level, translate the actual rates in terms of money into real rates, and compare
successive periods. Such comparisons are not very satisfactory, since no two periods, not even successive periods, are so alike industrially that we can say that they differ only as to the state of the monetary standard as reflected in the index numbers of prices. Of course, influences other than changes in money affect interest rates.
Detailed tables showing the average annual rate of change in the commodity price level,
*52 the rates of money interest, and the rates of real interest for London, New York, Berlin, Paris, Calcutta, and Tokyo are given in basic tables in the Appendix to this chapter. Wholesale commodity prices were used in computing these rates although cost of living indexes would have been preferable for this purpose and more in harmony with my theory of income. But cost of living indexes do not exist for the period covered.
Chart 42 shows the annual rate of change in the commodity price level (upper part) compared with the market rates of interest (lower part) in the London market over the period 1825 to 1927. The chart also gives the real rate by a dotted line, but this may, for the present, be overlooked.
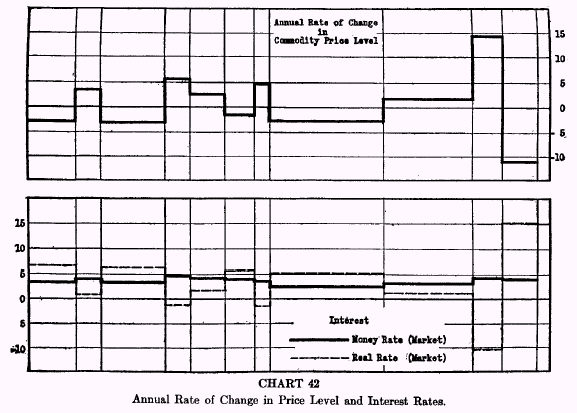
It will be observed that the entire period is broken up into sub-periods, which conform to rather definite and successively contrasted price movements. These sub-periods were allowed to choose themselves, so to say. That is, they were so chosen that each period should show a rather distinct change in the rate of price change as compared with the preceding and succeeding periods.
The periods were not chosen with any reference to, or indeed with any knowledge of, how the choice would affect the comparisons to be made. For example, the period 1825-1834 was a period during which commodities at wholesale fell at the average (annual) rate of 3.0 per cent per annum; this is plotted on the chart, in the usual way, by a horizontal line 3.0 points below the zero line. In the period 1834-1839 prices rose at the rate of 3.3 per cent per annum; this is plotted on the chart by a horizontal line 3.3 points above the zero line.
A brief glance at Chart 42 reveals that when the rate of price change
falls from one period to the next, the money rate of interest usually
falls, and when the rate of price change
rises, the interest rate usually
rises also. The comparison of each period with the one following may be designated as a sequence. In London eight such sequences out of ten for bank rates, and nine out of ten for market rates support the theory that money interest rates move in the same direction as the price level.
Comparisons of price change rates and interest rates have also been made for New York, Berlin, Paris, Calcutta, and Tokyo. The results, favorable and unfavorable, of all these comparisons are summarized in Table 13.
| TABLE 13 Sequences, Favorable and Unfavorable |
|||||||
|---|---|---|---|---|---|---|---|
|
|
|||||||
| London
|
Berlin
|
Paris
|
N. Y.
|
Calcutta
|
Tokyo
|
Total
|
|
| Favorable | 17 | 10 | 0 | 4 | 6 | 1 | 38 |
| Unfavorable | 3 | 2 | 1 | 3 | 3 | 3 | 15 |
Of the sequences compared, 38 support and 15 oppose the theory propounded. Thus, the favorable sequences are two and a half times as numerous as the unfavorable
sequences. This is a large preponderance, especially when we consider that there are so many inexactnesses in the statistical data and so many other causes affecting the rate of interest besides changes in the price level.
The same result may be expressed in terms of correlation coefficients. When we correlate interest rates with price changes for the important industrial countries (England, Germany, United States), fairly high coefficients (about +0.7) are obtained. Correlating the first differences, that is,
changes in interest rates and rates of price changes, likewise, shows a fairly high relationship in accord with the theory. However, the correlation for the data of all countries combined is insignificant. For all the countries studied we find +.036; for the corresponding first differences, -.165. It is seen that the well defined movements of prices and interest in the principal countries are largely offset by the movements in the countries of lesser economic importance. To obtain more decisive evidence upon the relationship studied, it is necessary to resort to the more rigorous analysis given in subsequent sections.
The evidence obtained from the comparisons in this section indicate that there is a very apparent, though feeble, tendency for the interest rate to be high when prices are rising, and the reverse. The adjustment is imperfect and rather irregular, but in the great majority of cases the tendency is evident.
§5. Real Interest Varies More Than Money Interest
If perfect foresight existed, continuously rising prices would be associated
not with a continuously rising rate of interest but with a continuing high rate of interest, and falling prices would be associated not with a continuously
falling rate of interest but with a continuing low rate of interest, and a constant price level would be associated with a constant rate of interest—assuming, in each case, that other influences than price change remained the same.
This perfect theoretical relationship of interest rates to price levels, assuming perfect foresight, is shown in Chart 43, showing high (not rising) interest rates while prices are rising, and low (not falling) interest rates while prices are falling. The real rate would remain constant at, say, 5 per cent under the ideal conditions here assumed.
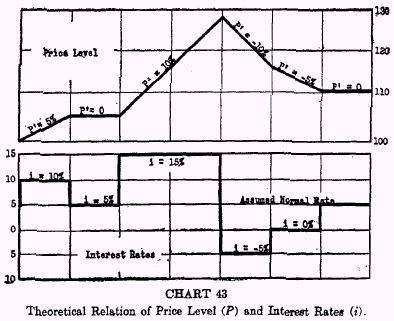
In this chart,
i stands for interest rate and
P‘ for price change, but the upper line indicates the price level. When
in the first period the price level rises, the price change (
P‘) is assumed to be at the rate of 5 per cent per annum. In the next period, the price level remains constant so that price change is zero, and so on as indicated. The lower curve shows the theoretical effects on the rate of interest. In the first period, it would be 5 per cent above normal; in the second period, normal; and so on.
One obvious result of such an ideally prompt and perfect adjustment would undoubtedly be that money interest would be far more variable than it really is and that when it was translated into real interest this real interest would be comparatively steady. What we actually find, however, is the reverse—a great unsteadiness in real interest when compared with money interest.
Real interest, however, as shown by the dotted lines on Chart 42, changed in the opposite way to money interest, due to the lack of foresight and adjustment. Attention is called to the period 1852-1857 in London, during which prices rose very fast (that is, money depreciated) simultaneously with, and mainly because of, the great gold production. The market rate of interest averaged 4.7 per cent, which was higher than in any subsequent or in any previous period. Yet during this period of apparently highest interest rates, lenders were receiving, in real interest, less than nothing for their savings. Also in the inflation period 1914-1920, bank rates reached their highest peak, 5.2 per cent, while average market rates, at 4.4 per cent, were but little lower than in 1852-1857. Yet in terms of real commodities those who saved and deposited or invested at the bank rates or market rates of interest were mulcted 9 to 10 per cent for their abstinence and sacrifices. In the following period, 1920-1927, however, the savers and lenders got back more
than all they, or their predecessors, lost in the previous period. The tremendous fall in prices in 1920 and 1921 boosted the real interest rate above 15 per cent. Thus the computed real rate is exceedingly erratic during a serious inflation or deflation.
Chart 44 represents in a different way the same theoretical relationship between price change and the rate of interest as that depicted on Chart 43. In Chart 44, price change (
P‘) is represented not by the slope of a line, but by distance measured above or below the zero line. Thus when the price level is rising at the rate of 5 per cent per annum,
P‘ is represented by a horizontal line 5 per cent above zero. When prices are stationary,
P‘ drops to zero, and so on. If men had perfect foresight, they would adjust the money interest rate so as exactly to counterbalance
or offset the effect of changes in the price level, thus causing the real interest rate to remain unchanged at the normal rate.
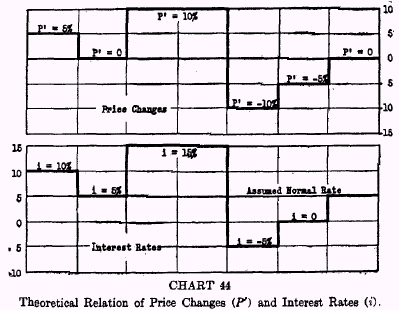
The following table shows that the standard deviation from the mean is far greater for the computed real rate of interest than for the actual rate of interest.
| TABLE 14 Standard Deviations of Money Interest and Real Interest |
||||
|---|---|---|---|---|
|
|
||||
| Number of Periods
|
Standard Deviations
|
|||
| Market Interest
|
Computed Real Interest
|
|||
| London | 11 | .62 | 6.1 | |
| New York | 8 | 1.07 | 8.5 | |
| Berlin | 7 | .73 | 5.0 | |
| Calcutta | 11 | .57 | 7.5 | |
| Tokyo | 5 | .69 | 7.0 | |
This table shows that the real rate of interest in terms of commodities is from seven to thirteen times as variable as the market rate of interest expressed in terms of money. This means that men are unable or unwilling to adjust at all accurately and promptly the money interest rates to changed price levels. Negative real interest could scarcely occur if contracts were made in a composite commodity standard. The erratic behavior of real interest is evidently a trick played on the money market by the “money illusion” when contracts are made in unstable money. The computed real rate of interest was
minus 7.4 per cent in New York in the period 1860-1865 and was still lower during 1915-1920. The rate was nearly minus 100 per cent in Germany during the period of most rapid inflation.
Another symptom of the same imperfection of adjustment
is the fact that the adjustment is very
slow. When prices begin to rise, money interest is scarcely affected. It requires the cumulative effect of a long rise, or of a marked rise in prices, to produce a definite advance in the interest rate. If there were no “money illusion” and if adjustments of interest were perfect, unhindered by any failure to foresee future changes in the purchasing power of money or by custom or law or any other impediment, we should have found a very different set of facts.
§6. Interest Rates and Rates of Price Change
The roughness of the comparisons between interest rates and price levels thus far made impels to further study of this important problem. For these more rigorous comparisons, the statistics of prices and of bond yields in Great Britain and the United States have been taken, being the only reliable statistics ready at hand which permit of long trend comparisons.
Since the theory being investigated is that interest rates move in the opposite direction to changes in the value of money, that is, in the same direction as price changes, the first analysis made is the same as that already made by rougher methods, the comparison of
price changes with interest rates.
For the rate of change of prices, the customary link relative expression was at first used in a preliminary study of quarterly United States data for the period 1890-1904. But to ensure full comparability with my related studies of several years ago on price changes and trade variations, the symmetrical expression
P‘ (rate of price change per annum) is used throughout. The precise derivation of
P‘ is given in my paper,
Our Unstable Dollar
and the So-Called Business Cycle.*53 The upper part of Chart 45 gives the correlation coefficient (
r) obtained by correlating the long term interest rates as reflected in the yield of British consols with percentage changes in prices computed from the British wholesale index numbers of Sauerbeck and The Statist.
*54 The lower part of this chart gives the
r‘s for bond yields and percentage price changes in the United States.
*55
In Great Britain, the price changes from 1820 to 1924 fall into three clearly defined periods, namely, 1820 to 1864, a period of fluctuating prices with no marked upward or downward trend in prices; 1865 to 1897, a period of declining prices; 1898 to 1924, a period chiefly of rising prices, including a big boom from 1915 to 1920, followed by a crash and more stable prices since 1922.
A very brief examination of the charts below indicates that there is little or no
apparent relationship between
price changes and interest rates in any of the periods studied in either country except for 1898-1924 in Great Britain. For the period 1820-1864 in Great Britain we obtain a maximum inverse correlation of -0.459, without lagging. For the period 1898-1924, we get as a maximum +0.623 when
i is lagged 4 years and +0.678 when
i is lagged 6 years. Lag means the time interval between a
price change and the associated change in the interest rate. Chart 45 shows the results of lagging interest rates behind price changes on the one hand and lagging price changes behind interest rates on the other. For the United States, without lagging,
r = +0.289, while the highest correlation is +0.406 when
i is lagged 4 years. These results suggest that no direct and consistent connection of any real significance exists between
P‘ and
i.
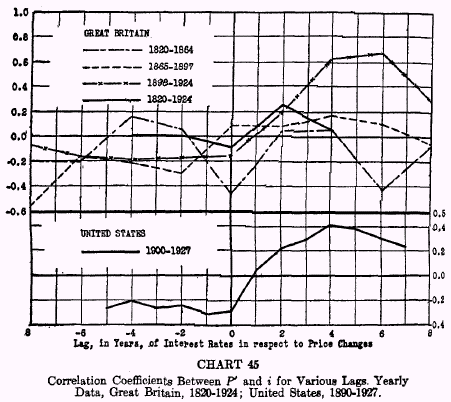
The variations in
r for different lags may be due to the zigzag cycles in the data correlated. The maximum value
of
r establishes definitely that, characteristically, movements in
i lag behind corresponding movements in
P‘. The small numerical value of
r suggests that the relation can be revealed only faintly by
P‘ and
i directly. But a little consideration suggests that the influence of
P‘ or
i may be
assumed to be distributed in time—as, in fact, must evidently be true of any influence. This hypothesis proved quite fruitful in my studies several years ago, in the course of which the theory of
distributed influence or, if we wish to avoid the implication of cause and effect, of
distributed lag was developed in considerable detail.
*56
The reader may consult the references cited for details. It must suffice here to point out only the essence of the transformation of
P‘ into the derived quantity
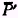 , measuring the distributed influence of sundry
, measuring the distributed influence of sundry
P‘. Arithmetically,
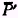 is merely a certain weighted average of sundry successive
is merely a certain weighted average of sundry successive
P”s. (See (
a) and (
b) referred to in the footnote.) In any specific problem the number of successive
P”s that enter into the average
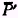 ‘s depends on the length of the time interval during which the influence of any
‘s depends on the length of the time interval during which the influence of any
P‘ is
assumed to be perceptible. The weights used vary in a certain functional form, generally that of a skew probability curve. Thus, in applying the theory at least two parameters are involved: (1) the length of the influence interval (which determines the number of
P”s
that enter into the composite
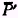 ), and (2) the form of variation of the weights. As indicated in reference (
), and (2) the form of variation of the weights. As indicated in reference (
b) in the above footnote, the form of variation of the weights is exactly—but in reverse order—the form in which the distributed influence of any
P‘ tapers off during successive periods of time.
*57
In the present study we must limit our investigation to only one type of distribution of influence and variation of weights. The form chosen is the simple straight line function or arithmetical progression which proved most effective and easily calculated in my 1925 study. Several periods of influence range, however, were tried. The results for the British and American yearly data are shown in Charts 46 and 47.
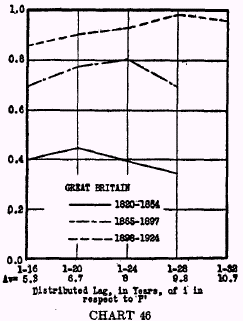
Correlation Coefficients Between
and
i for Various Distributions of Lag.
is the Combined Effect at Any Point of Time of the Influence of Preceding
P‘ ‘s with Lags Distributed. Yearly Data, Great Britain, 1820-1924.
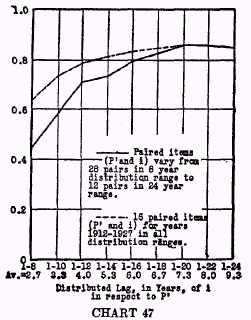
Correlation Coefficients Between
and
i for Various Distributions of Lag.
is the Combined Effect at Any Point of Time of the Influence of Preceding
P‘ ‘s with Lags Distributed. Yearly Data, United States, 1900-1927.
The figures at the bottom of Charts 46 and 47 refer to the number of years over which the effect of price changes is taken into account in the correlations between
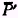 and
and
i. For example, in Chart 46, the figures 1-16 mean that the
effect of a price change is assumed to begin the first year after the change and to cease at the end of 16 years. The weighted average of the distributed lag is 5.3 years. The longest distribution shown at the right is from 1 to 32 years, or a weighted average of 10.7 years.
The charts picture only the effects of the distributed lag when interest rates follow behind price changes.
Experiment proved that when price changes were lagged behind the distributed influence of changing interest rates, the correlation coefficients were too small to have any significance.
The high and consistent correlations shown in the
above charts are in striking contrast to the results previously obtained from correlating
P‘ directly with
i. The assumption that a change in prices occurring during one year exhausts its influence upon interest rates in the same year or in another single year is shown to be quite wrong, as might be expected. Our first correlations seemed to indicate that the relationship between
P‘ and
i is either very slight or obscured by other factors. But when we make the much more reasonable supposition that price changes do not exhaust their effects in a single year but manifest their influence with diminishing intensity, over long periods which vary in length with the conditions, we find a very significant relationship, especially in the period which includes the World War, when prices were subject to violent fluctuations.
The British figures for 1820-1864 give the lowest correlations of any included in this study. These low figures are possibly due in part to the less accurate price indexes in those early years. It is noteworthy that the correlation coefficients are distinctly lower for the United States in the period 1900-1927 than they are for Great Britain in the period 1898-1924. It is also interesting that for Great Britain in 1898-1924, the highest value of
r (+0.980) is reached when effects of price changes are assumed to be spread over 28 years or for a weighted average of 9.3 years, while for the United States the highest
r (+0.857) is for a distribution of the influence due to price changes over 20 years or a weighted average of 6.7 years.
Chart 48 shows graphically the smoothing effect of distributing the influence of
P‘ over various periods.
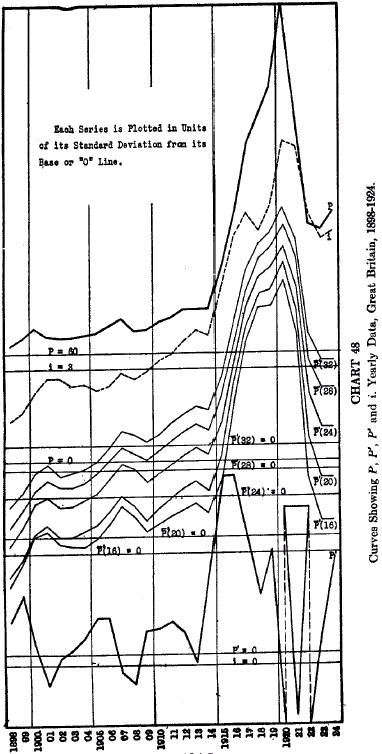
By assuming a distribution of effect of price changes over several years according to the form described above, the relationship between price changes and interest rates
which was only faintly revealed by the first direct comparisons is clearly revealed. The high correlation coefficients obtained by means of the method of distributing the influence of
P‘ and
i show that the theory tested in this chapter conforms closely to reality, especially during periods of rather marked price movements.
Furthermore the results and other evidence, indicate that, over long periods at least, interest rates
follow price movements. The reverse, which some writers have asserted, seems to find little support. Experiments, made with United States short term interest rates, to test the alternative hypothesis of distributed influence of interest rate changes instead of price changes, gave results of negligible significance. Our investigations thus corroborate convincingly the theory that a direct relation exists between
P‘ and
i, the price changes usually preceding and determining like changes in interest rates.
§7. Short Term Interest Rates and Prices in the United States
A study of short term commercial paper rates in relation to short term price movements corroborates the evidence obtained from correlating long term interest rates and price changes. The New York interest rates on short term commercial paper have been correlated with changes in the quarterly wholesale price indexes computed from monthly indexes of the United States Bureau of Labor Statistics for the periods 1890-1914 and 1915-1927.
*58
On Chart 49 are plotted the curves showing the quarterly price indexes and the
P‘ and
P‘ derived from them, with the interest rates for the entire period 1890-1927.
P‘ is shown for 120 quarters or 30 years.
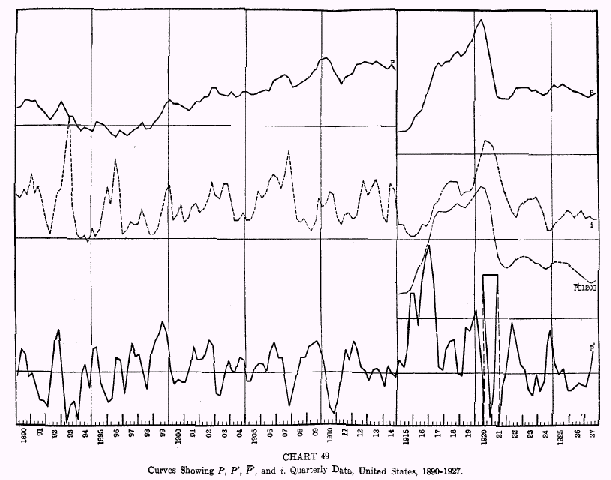
These curves of quarterly data tell much the same story as is told by the curves representing yearly data, shown in Chart 48, for Great Britain.
P‘ obviously corresponds much more closely to
i than does
P‘.
Chart 50 shows the rather erratic variation of the
r‘s computed from
i and
P‘ directly without distributing the effects of price changes.
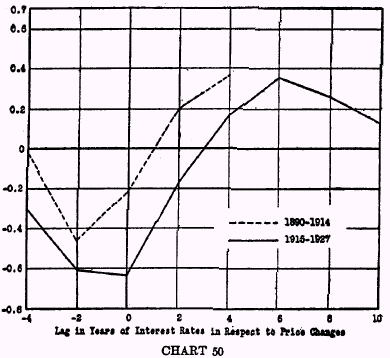
Correlation Coefficients Between
P‘ and
i: for Various Lags, Quarterly Data, United States, 1890-1927.
Chart 51, on the contrary, shows, in sharp contrast, the steady increase in
r computed from
i and price changes with influence distributed over periods from 20 to 120 quarters. This chart shows that, in the period 1915-1927,
r reaches its maximum (+0.738) only when a total of 120 quarters, or 30 years, is included in the period subject to the influence of price changes upon
i.
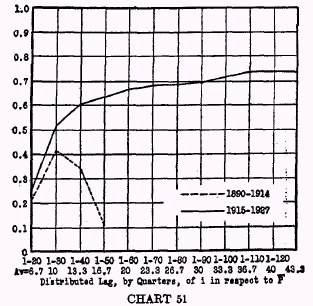
Correlation Coefficients Between
and
i for Various Distributions of Lags.
is the Combined Effect at Any Point of Time of the Influence of Preceding
P‘ ‘s with Lags Distributed. Quarterly Data, United States, 1890-1927.
The studies of both the long term and short term movements of prices and interest rates give very similar results. In both studies the
r‘s are insignificant when
P‘ and
i are correlated directly, either with or without lagging, so long as we ignore the fact that the effects
of price changes are distributed over many years. But when the effects of price changes are distributed, the
r‘s take on an entirely different aspect with an entirely new meaning, especially during the War period when prices fluctuated widely and quickly. It would seem then that price and interest fluctuations are governed by
one law, not, as has been suggested, by two different opposing laws, for short and for long periods of time.
It seems fantastic, at first glance, to ascribe to events which occurred last century any influence affecting the rate of interest today. And yet that is what the correlations with distributed effects of
P‘ show. A little thought should convince the reader that the effects of bumper wheat crops, revolutionary discoveries and inventions, Japanese earthquakes, Mississippi floods, and similar events project their influence upon prices and interest rates over many future years even after the original casual event has been forgotten.
*59 The skeptical reader need only be reminded that the economic effects
on the farmer of the deflation of 1920 are now, in 1929, sufficiently acute to make farm relief a pressing political problem and that these economic effects may be expected to persist for many years to come. A further probable explanation of the surprising length of time by which the rate of interest lags behind price change is that between price changes and interest rates a third factor intervenes. This is business, as exemplified or measured by the volume of trade. It is influenced by price change and influences in turn the rate of interest.
§8. Interest Rates and Price Indexes
Thus far we have considered the relation of changes in the price level and interest rates. It remains to study the relations of the
price levels themselves to interest rates. The same basic data are used as in the preceding sections, but we now correlate the price indexes directly with the interest rates in Great Britain and the United States.
Chart 52 shows the British long term interest rates (bond yields) plotted with the wholesale price index for the years 1820-1924.
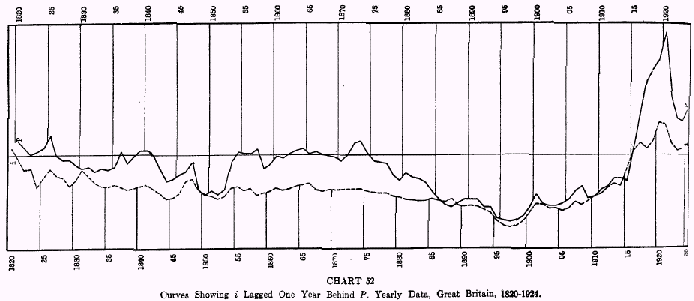
It is apparent that the
P curve and the
i curve, as plotted, conform very closely. Furthermore, lagging interest rates one year gives the highest obtainable degree of correspondence. The corresponding data for the United States, plotted on
Chart 57 below without lagging
i, shows the same close relationship between
P and
i.
On Chart 53 are plotted the curves of the correlation coefficients computed for
P and
i for Great Britain and the United States.
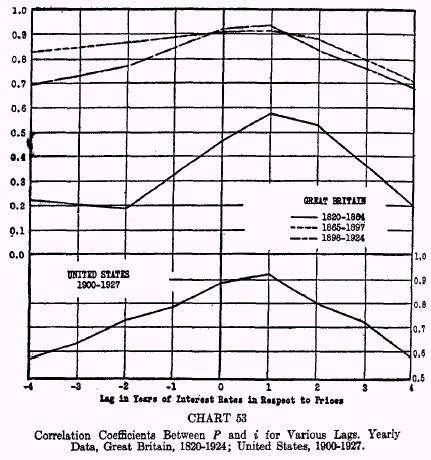
The
r‘s for the whole period 1820-1924 for Great Britain are not shown on Chart 53 since they reveal nothing
not shown by the
r‘s for the shorter periods. These highly significant correlations seem to establish definitely that over long periods of time high or low interest rates
follow high or low prices by about one year.
Comparison of short term interest rates with quarterly index numbers gives results of no significance for the period 1890-1914. On the contrary, the
r‘s obtained from
comparing these series over the period 1915-1927 are high; without lagging
r = +0.709; lagging one quarter,
r = +0.829; two quarters,
r = +0.891; four quarters,
r = +0.838. In both periods the coefficients of correlation grow smaller as the
P‘s are lagged behind
i, while they grow larger when
i is lagged behind
P. The results from the analysis of the short term data, while differing in some respects, may be said to confirm the results obtained from comparing the long term data.
§9. Elimination of Trends
These high correlations do not necessarily mean that the interest rate will always be high when prices are high and low when prices are low, but the tendency toward this is definitely established.
The correlations obtained for all periods and sub-periods considered are unusually high. It is necessary to guard against the possibility that these coefficients are of the familiar nonsense type, and are spuriously high because of the presence of
secular trend forces that affect both
P and
i. Due consideration was given to the control devices that have wide acceptance in the literature of statistics, such as “elimination of trend” and “seasonal” fluctuations. The general methodology of analysis of time series is still in the process of formulation. The specific problem of trend analysis is still largely unsolved.
*60 In the present case, it is rather doubtful that trend forces are involved which should be eliminated. What is desired in
all the preceding comparisons of price levels and interest rates is to discover what precise relation obtains between interest rates and prices
in the long run. It is like giving the play of
Hamlet without Hamlet to eliminate the secular trends of
i and
P from a study of long term relationships in which these very secular trends are most important and often dominant influences.
However, to anticipate possible criticisms and errors, the results of eliminating secular trends of prices and interest rates have been studied. These additional studies are also made for another and more important purpose, namely, to discover whether or not the shorter so-called
cyclical movements of prices influence long-term interest rates in the same way as the long
secular price movements have been shown to do. For simplicity, least square straight line and parabola trends were used. These will answer sufficiently the present purpose. In addition, a cubic trend was applied to the yearly data for the United States for the period 1900 to 1927 and to the British data for the corresponding period.
Charts 54, 55, and 56 show the curves of price levels and interest rates in Great Britain for the period 1820-1924 with straight line trends and parabolic trends plotted, while Chart 57 shows the corresponding curves for the United States for the period 1900-1927.
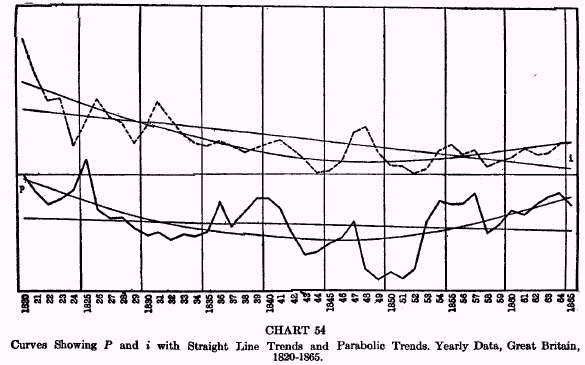
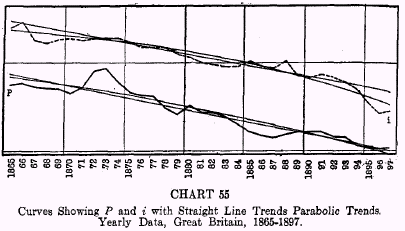
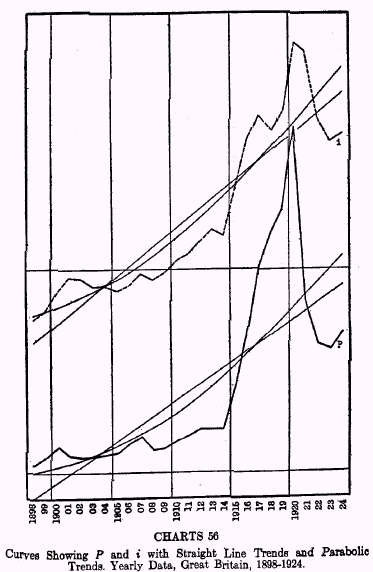
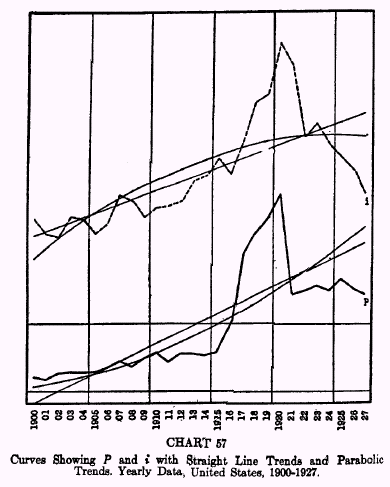
The results, after eliminating these secular trends, are interesting and amazing. The correlation coefficients with straight line trends eliminated are naturally smaller than when these trends are included, but they are still significantly high except for the period 1865-1897 in Great Britain. In the majority of cases, the characteristic lag of about a year of interest rates behind prices gives the highest correlation.
As a further test of the validity of the comparisons, the parabola trend deviations for the recent period, ending with the high point for both
P and
i in 1920, have been computed and plotted, though the charts are not here shown. It might be supposed that the elimination of a parabolic trend from these violently fluctuating series would leave only erratic wiggles in the
P and
i curves with little or no correspondence with each other. That price levels and interest rates are very closely related, even when great secular and cyclical forces are eliminated, is clearly demonstrated by the results of these investigations. The correlation coefficients obtained from the data for the period ending in 1920 with the parabolic trends eliminated are about +0.70, which certainly indicates that yearly fluctuations, as well as cyclical and secular trends, of prices and interest are generally in the same direction. The coefficients obtained from correlating
P and
i with straight line trends eliminated are plotted on Chart 58.
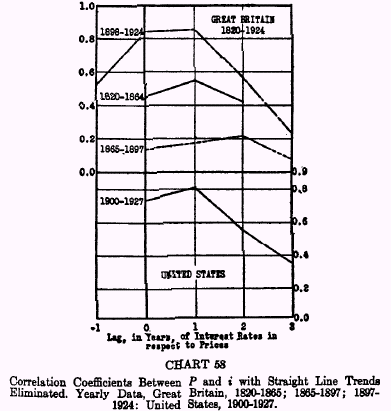
The reader will see that the
r‘s for the latest period are much higher than for the other periods. For Great Britain in the period 1898-1924,
r = +0.851 with
i lagged one year. For the United States for the corresponding period 1900-1927, and with the same lag of
i, we get
r = +0.806. It is not worth while to plot the
r‘s
with
P lagged behind
i, since it is apparent at a glance that
r decreases with the lagging of
P.
When the parabolic trend is eliminated, the correlation coefficients for the cycles become insignificant except for the period including the World War. The highest
r for the British data for 1820-1864 is +0.319 when
i is lagged one year; for 1865-1897, the highest
r is +0.045 with
i lagged two years; for 1898-1924,
r is +0.829 with no lagging, and +0.817 when
i is lagged one year. The
United States data give
r‘s of +0.695 without lag, and +0.876 with
i lagged one year. Even when a cubic trend is eliminated for 1898-1924 the
r‘s still remain significantly high, namely, without lagging,
r = +0.794 and with
i lagged one year
r = +0.790. For the United States without lagging,
r = +0.525 and with
i lagged one year
r = +0.769.
The elimination of the secular trends from the comparisons makes the relationship of
i and
P depend solely upon the similarity of fluctuations in the shorter or cyclical periods. Even without Hamlet the play proves to be astonishingly informing and interesting. It is quite definitely demonstrated that, in times of marked price changes, as in the World War period, the effects of price movements are felt rather quickly upon the rates of interest, even in the case of long term bond yields.
§10. Relations of Prices and Interest Interpreted
The studies of
P,P‘ and
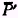 in relation to
in relation to
i have brought out four relationships:
(1) The rate of interest tends generally to be
high during a
rising price level and
low during a
falling price level;
(2) The rate of interest lags behind
P‘ so that often the relationship is obscured when direct comparison is made;
(3) The rate of interest correlates very markedly with
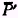 , representing the
, representing the
distributed effect of lag. For recent years in Great Britain, the close relationship is indicated by
r = +0.98 when
i is lagged and the effects of
P‘ are distributed over 28 years;
(4) The rate of interest tends definitely to be
high with a
high price level and
low with a low price level.
We have also seen that the first three sets of facts fit in with the analysis presented, the first corresponding, although only roughly, with the ideal assumption of perfect foresight and adjustment, the second and third corresponding to the more realistic assumption of imperfect foresight and delayed, but accumulated, adjustment.
Two facts have, I think, now been well established. The first, that price changes influence the volume of trade, has been shown in earlier studies made by me.
*61 The second, that the volume of trade influences the rate of interest, has been shown by Carl Snyder,
*62 Col. Leonard Ayres,
*63 Prof. Waldo F. Mitchell,
*64 and others.
The evidence for both relationships is not only empirical but rational. Rising prices increase profits both actual and prospective, and so the profit taker expands his business. His expanding or rising income stream requires financing and increases the demand for loans.
In my study of the so-called business cycle, the lag of volume of trade,
T, behind price changes when the influence of
P‘ was distributed over a range of 25 months, was found to have a modal value of 9½ months. The
lag of
i behind
T using a simple lag was found by Carl Snyder to be 10 to 15 months, by Leonard Ayres to be about 14 months and by Waldo F. Mitchell about 6½ months.
If we add the lag of
T behind
P‘ which I found to be over all about 25 months, and the lag of
i behind
T of 14 months, found by Snyder and Ayres, we obtain a combined lag of
i behind
P‘ of 39 months. This combined lag obtained by simple addition is far shorter than the lags discovered in the calculations presented above, whether for yearly or for quarterly price changes in relation to
i. Apparently the double distribution of the lag of
T behind
P‘ and again of
i behind
T may result in a greater lag than would be obtained by simple addition.
The fourth relationship stated above must be, I think, regarded as an accidental consequence of the other three. At any rate, it seems impossible to interpret it as representing an independent relationship with any rational theoretical basis. It certainly stands to reason that
in the long run a high level of prices due to previous monetary and credit inflation ought not to be associated with any higher rate of interest than the low level before the inflation took place. It is inconceivable that, for instance, the rate of interest in France and Italy should tend to be permanently higher because of the depreciation of the franc and the lira, or that a billion-fold inflation as in Germany or Russia would, after stabilization, permanently elevate interest accordingly. This would be as absurd as it would be to suppose that the rate of interest in the United States would be put on a higher level if we were to call a cent a dollar and thereby raise the price level a hundredfold. The price level as such can evidently have no permanent influence on the rate of interest except
as a matter of transition from one level or plateau to another.
The
transition from one price level to another may and does work havoc as we have seen, and the havoc follows with a lag which is widely distributed. The result is that during a period of inflation the interest rate is raised
cumulatively, so that at the end of this period when the price level is high, the interest rate is also high. It would doubtless in time revert to normal if the new high level were maintained, but this seldom happens. Usually prices reach a peak and then fall. During this fall the interest rate is subject to a cumulative downward pressure so that it becomes subnormal at or near the end of the fall of prices. Thus, at the peak of prices, interest is high, not because the price level is high, but because it has been rising and, at the valley of prices, interest is low, not because the price level is low, but because it has been falling.
Another consideration seems to complete the explanation of the close association between high and low price levels with high and low interest respectively. This is the necessity for banks to cope with maladjustments following inflation and deflation. Mr. R. G. Hawtrey has emphasized this point in a letter to me, and I have summarized his views almost in his own words:
When credit is expanding, the rising price level and high profits bring about a high rate of interest. When the expansion has reached, the limit permitted by the stock of gold, the rate of interest is put
still higher in order to bring about a
fall in the price level. When the fall in prices takes effect, a low rate of interest becomes appropriate, and when credit contraction has proceeded so far that a redundant supply of gold has accumulated, the rate of interest is depressed still lower in order to bring about a renewed rise in the price level. Thus a high rate of interest corresponds first with rising,
then with falling, prices, and so synchronizes with high prices. A low rate of interest corresponds first with falling, and then with rising, prices, and so synchronizes with low prices.
The process of inflation boosts both prices and interest, until a still further boost of interest is made by the banks in order to stop the over extension, leaves a peak of prices with high interest before, at, and after that peak, while, contrariwise, the process of deflation reduces both prices and interest until a still further reduction of interest is made by the banks in order to stop the depression, leaves a valley of prices with low interest before, at, and after the valley.
Such considerations seem to be sufficient to explain the otherwise puzzling and apparently irrational coincidence which we have so often found to exist between high and low prices and high and low interest rates.
The only alternative interpretation of which I can think is that a high or low price level is not a monetary and nominal affair but a matter of real commodities. Sometimes, as in France and Italy just cited, the high prices may be closely associated with impoverishment. If it were true that a high price level usually signified a real scarcity of goods—a low income stream—while a low price level usually signified relative abundance, we could explain our puzzle by the relation of time preference to the size of the income stream. But the facts in general do not seem to justify such an interpretation,
*65 least of all in the United States in the War years when the correlations are the highest. During that period, incomes increased at a tremendous rate, and interest rates advanced
pari passu.
§11. Relations of Interest to Business and Prices
As implied by what has just been said regarding banking policy, the relationships of
P‘ and
i are mutual. A change in
i undoubtedly has an effect upon
P‘ as well as the reverse. Our analyses have demonstrated that, in a decisive majority of instances, price changes precede changes in
i. This does not mean that changes in the interest rate can never be used to forecast changes in prices and in business activity.
*66 In fact, an arbitrary increase in
i at any time does tend to pull down the level of general commodity prices, while a decrease in
i tends to increase
P. This is a fact which has been quite well established and is made use of by central banks in formulating their banking and credit policies.
The influence of changes in interest rates upon prices and business activity is made use of also by forecasting agencies in making their prognostications of business and price movements for the near future.
*67 The fact that
i follows
P‘, in most instances over secular and cyclical periods, is not inconsistent with the other fact that every increase or decrease in
i exerts an influence upon
P in the
opposite direction. Within limits, a fall in the rate of interest may and often does produce a rise in prices and in business activity almost immediately. This effect may be continued for many months until increased prices again become dominant and pull the interest rate up again.
In so far as the rate of interest is cause and the price movements are effect, the correspondence is
just the opposite of that which occurs in so far as the price movements are cause and the interest movements effect.
It is outside the scope of this treatise, which has to do only with things which affect the theory of the rate of interest, to attempt to explain fully all the very complicated relations connecting interest and business. The studies completed or in progress in my office show some interesting results which I hope to publish later.
It is unfortunate that many students in this field seem to take it for granted that there is one and only one definite cycle, or that the cycle is controlled by one and only one definite influence. I have been accused of inconsistency for presenting several seemingly incompatible theories concerning the business cycle. As a matter of fact, I have never as yet studied the so-called business cycle as a whole. I have only studied a few of its elements or aspects.
*68
§12. Interest Rates and Bank Reserves
That there is a relationship between bank reserves and the rate of bank discount is perhaps self-evident. Every banker and business man is familiar with it. J. P. Nor
ton
*69 found such a correlation and the relationship finds expression in practically every treatment of commercial banking.
This relationship furthermore carries over into the rates fixed on commercial paper. Mr. W. Randolph Burgess
*70 has made a study of this relationship which he expresses briefly as follows:
“Banks are the custodians of money in this country. When the bankers have much money to lend,
money rates tend to be easy; when they have little to lend, money rates tend to be firm. The amount a banker can lend depends upon his reserve position. Therefore, the reserve position of the banks of the country determines short term money rates, and the causes of changes in money rates are to be found in the causes of changes in the reserve position of banks.”
Mr. Burgess presents an impressive inductive verification of this theory for the period 1904 to 1909 by comparing the changes in the short term money rate with the changes in the average surplus or deficit in the reserves of New York City Clearing House Association Banks.
The same relationship, Mr. Burgess finds, obtains under the Federal Reserve System between the excess or deficit in reserves of twenty-three New York City Banks and the closing call money rate for intra-week periods between the balancing of the reserves by the Federal Reserve Banks. Over longer periods of time, the relationship is shown by the similarity in the movement of the open
market interest rate for prime 4-6 months commercial paper and the average daily bills discounted for member banks by all Federal Reserve Banks.
The Federal Reserve Act requires the pooling of member banks’ reserves with the Federal Reserve Banks. These reserves must average the minimum legal requirements and balancing periods are maintained once a week in large cities and twice a month elsewhere. Surplus and deficit reserves are, therefore, impossible for periods of more than two weeks at the very maximum under this system. But the influence of the banks on the money market rates are now effected through borrowings at the Federal Reserve Banks. Thus a period of member banks borrowing corresponds in its relation to the money market to a period of deficit reserves under the National Banking Act, and a period when member banks are paying off their loans at the Reserve Bank corresponds to a period of excess reserves.
A similar correspondence between commercial paper rates and gold reserves is shown by a recent study by Colonel Leonard Ayres, of the Cleveland Trust Company.
*71
Curiously enough, this well known and sound relationship between bank reserves and interest rates is often confused with the entirely different, generally incorrect, but commonly believed proposition that the rate of interest is high when money in general is scarce, and low when money in general is abundant. The thought seems to be if the rate of interest is called the price of money it is natural to conclude that abundance of money, like abundance of wheat or anything else, makes its price low, while scarcity of money makes its price high.
But the price of money in the sense of the rate of interest is a very peculiar kind of price. It is, as we know, the deviation from par of the price of present money in terms of future money. It is not very analogous to the price of wheat. The real analogy with the price of wheat is not the rate of interest but the
purchasing power of money. In that sense it is perfectly true that the price of money is high or low with its scarcity or abundance. But in the other sense it is not true. Moreover, as we have seen, when the price of money, in the sense of the purchasing power of money, is low, that is, when the price level is high, and when, therefore, presumably the quantity of money is large, we do not then find the rate of interest low, as the theory outlined above requires. On the contrary, we find a high price level associated with a high interest rate.
That short term interest rates vary inversely with bank reserves, however, fits in with our theory of interest as related to real income. A low bank reserve is, among other things, a symptom of a prospective general increase in the income of the community. When business is optimistic, which means when future income looms large, there is an impatient desire to discount that big future and to make it even bigger by investing present income, provided the investment can be financed. Evidently the immediate effect is to increase bank loans and consequently to increase deposits. These results tend to lessen the ratio of bank reserves to liabilities. Thus the banker is led to raise his rate. It
seems that the rise merely reflects his reserve situation. But back of this situation is the demand for loans, and back of that something more fundamental—the rising income stream, a period of increasing prosperity, of invention and progress, or of great financing.
From these changes, rather than from a merely technical banking situation, come high rates of interest.
Thus the banker registers the effect of the increasing income stream. The reverse situation of descending income stream, lessened opportunity to invest, lessened loans and deposits, tend toward idle reserves and low interest.
Normally the banking function should do little more in relation to the rate of interest than to transmit the effects of the income stream. This would be substantially the case if we had a scientific adjustment of the ultimate source of bankers’ reserves, the world’s supply of monetary gold. If this were so adjusted as to maintain a constant purchasing power of that gold and so of money units, the banker could be trusted to adjust properly, even if unconsciously, the rates of interest to the income situation of the country.
Unfortunately, we do not yet have such a scientific currency system, but are still exposed to every wind that blows in the gold bullion market. The consequence is that superimposed on the normal credit operations are abnormal ones by which the rate of interest is perverted through the very banking machinery which should make it normal.
Banking thus becomes, in practice, not simply a register of fundamental economic influences, not merely their facilitator, but a most powerful independent influence. Practically, then, the banking machinery often interferes with, rather than transmits, the normal influence of society’s income situation. If the gold mines become depleted, gold reserves become inadequate to support the growing inverted pyramid of credit based upon it and required by the expanding income of society. The banker
then has no choice, under the law, but to raise his rates in self-defense. The result is a shrinkage of credit when an expansion is needed, a fall of prices and high bank rates at the very time that low money rates of interest are needed. The real rates are then doubly high—high because the money rates are high and still higher because of the appreciation of money.
These maladjustments are largely responsible for the so-called business cycle. When they are serious, not only are the consequences disastrous but there is little then left in the market figures of interest to register the influence of fundamental income conditions.
*72 The interest rate then registers, rather, a choking or stalling of the banking machinery. In an acute panic, scarcity of money itself has made interest high. Money of any kind brought into the market at such times will relieve the stringency and lower the rate of interest. To relieve the money stringency, the United States has, in times past, poured money into the channels of trade by prepaying interest on bonds, and clearing houses have accomplished it by issuing clearing house certificates.
The establishment of the Federal Reserve System has stabilized prices and interest rates in the United States, although the cataclysm of war in 1914-1921 upset the price level and the normal correspondence between real and money rates of interest as they had never been upset before.
At present, the Federal Reserve System exerts a normalizing influence and seems to be groping to apply the
stabilizing principles which for many years have been suggested by Wicksell, Cassel, and other economists.
Even these efforts, while in the end they save us from price convulsions and real-interest convulsions, nevertheless themselves involve a slight interference with the natural effects of the income situation. The rediscount rate, when raised, restricts credit and stops price inflation; and when lowered, liberates credit and stops price deflation. As the effect, in either case, tends to be cumulative as long as the slight artificial raising or lowering is in force, the interference with the normal course of events need only be slight, almost negligible. It would not be surprising if a difference of one half of 1 per cent from an ideally normal rate should prove usually sufficient. Maintained sufficiently long, this deviation from a normal interest rate may prevent a very abnormal deviation in our monetary standard.
Some slight interferences are inherent in any such banking system, not only as an incident to the supremely important function of preventing inflation and deflation, but also as a necessary price to pay for the very existence of a banking system. In order to maintain a liquid condition and to avoid risk of bankruptcy, each bank must occasionally put its loan policy out of line with the ideal requirements of the income situation.
But, as we gradually perfect our banking technique and policies, we shall get closer and closer to a condition in which the rate of interest as a whole will reflect the income influences discussed in this book. The money rate and the real rate will become substantially the same, and any action of the banker which can be called an interference with, rather than a registering of, fundamental economic conditions will become almost negligible.
§13. Summary
We have found evidence general and specific, from correlating
P‘ with both bond yields and short term interest rates, that price changes do, generally and perceptibly, affect the interest rate in the direction indicated by
a priori theory. But since forethought is imperfect, the effects are smaller than the theory requires and lag behind price movements, in some periods, very greatly. When the effects of price changes upon interest rates are
distributed over several years, we have found remarkably high co-efficients of correlation, thus indicating that interest rates follow price changes closely in degree, though rather distantly in time.
The final result, partly due to foresight and partly to the lack of it, is that price changes do after several years and with the intermediation of changes in profits and business activity affect interest very profoundly. In fact, while the main object of this book is to show how the rate of interest would behave if the purchasing power of money were stable, there has never been any long period of time during which this condition has been even approximately fulfilled. When it is not fulfilled, the money rate of interest, and still more the real rate of interest, is more affected by the instability of money than by those more fundamental and more normal causes connected with income impatience, and opportunity, to which this book is chiefly devoted.
Legal Tender Notes in California, Quarterly Journal of Economics, October, 1892, p. 15.
Official Intelligencer (1894), p. 75.
Report of the Indian Currency Committee (1893), p.27, but it is corrected to apply to calendar instead of official years.
Appreciation and Interest, but are not reproduced here.
The Future Course of High Class Investment Values, The Bankers’, Insurance Managers’ and Agents’ Magazine, January, 1923, p. 15. Reprinted in revised form in The Spectator, March 7, 1925.
The Business Cycle Largely a “Dance of the Dollar,” Journal of the American Statistical Association, December, 1923, p. 5, top paragraph; (b)
Fluctuations in Prive-Levels in The Problem of Business Forecasting by Warren M. Persons, William T. Foster, Albert Hettinger. Boston, Houghton Mifflin Company, 1924, pp. 50-52; and particularly, (c)
Our Unstable Dollar and the So-Called Business Cycle, Journal of the American Statistical Association, June, 1925, pp. 179-202.
m pertaining to the month t
m exerts an influence, F(t
m +
l), whose intensity is proportional to 8 during t
m+3, to 7 during t
m+4,…, to 1 during t
m+10, to 0 during t
m+11.
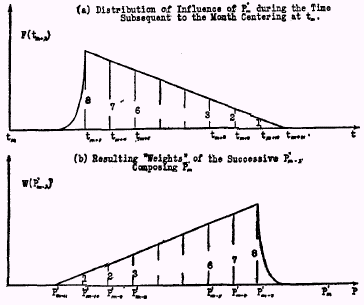
Conversely the aggregate influence on the affected variable during the month t
m consists of the various P’
m-
l which enter with the following weights tapering off in arithmetical progression; P’
m-3 with weight 8, P’
m-4 with weight 7,…., P’
m-10 with weight 1, P’
m-11 with weight 0. The numerical measure of this composite influence is:
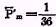 [8 P’
[8 P’m-3 + 7 P’
m-4 +… + 1P’
m-10 + 0 P’
m-11],
the divisor 36 being the sum of the weights,
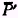 . For example, in the case of a 20 term influence-range straight line distribution,
. For example, in the case of a 20 term influence-range straight line distribution,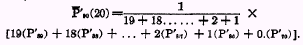
It is evident, and I have tested it thoroughly, that the composite
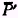 would be only slightly changed if the tail half of the distribution were omitted. The distribution in the above example would then be,
would be only slightly changed if the tail half of the distribution were omitted. The distribution in the above example would then be,
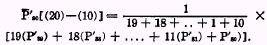
For the United States yearly data 1890-1927, the correlation of
i and
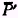 with an influence range of 20 years was r = + 0.857. For this distribution truncated by chopping off the end quarter, r = +0.843; the end half, r =+0.798; and the end three quarters r =+0.439.
with an influence range of 20 years was r = + 0.857. For this distribution truncated by chopping off the end quarter, r = +0.843; the end half, r =+0.798; and the end three quarters r =+0.439.
The Variate Difference Method, Biometrica, Vol. XIV, 1923, pp. 281-309; W. M. Persons,
Statistics and Economic Theory, Review of Economic Statistics, Vol. VII, No. 13, July, 1925, pp. 179-197; Anderson,
The Decomposition of Statistical Series into Components, Journal of the Royal Statistical Society, Vol. XC, pt. 3, 1927, pp. 548-570.
Our Unstable Dollar and the So-Called Business Cycle, Journal of the American Statistical Association, June, 1925, pp. 181-202;
A Statistical Relation Between Unemployment and Price Changes, International Labour Review, Vol. XIII, No. 6, June, 1926, pp. 785-792.
The Influence of the Interest Rate on the Business Cycle, American Economic Review, Vol. XV, No. 4, Dec., 1925, pp. 684-699;
Interest Rates and the Business Cycle, American Economic Review, Vol. XVI, No. 3, Sept., 1926, pp. 660-663.
Interest Cost and the Business Cycle, American Economic Review, Vol. XVI, No. 2, June, 1926, pp. 209-221;
Supplementary Note on Interest Costs, American Economic Review, Vol. XVI, No. 3, Sept., 1926, pp. 451-452.
The Money Illusion. New York, Adelphi Company, 1928, pp. 41-42.
Geldzins und Güterpreise; Prof. Alfred Marshall, Prof. Gustav Cassel, Rt. Hon. Reginald McKenna, Chairman of the Midland Bank of London, Mr. R. G. Hawtrey, of the Treasury of Great Britain, and many other well known economists, bankers, and business men have emphasized that business activity is influenced and may be largely controlled by manipulation of the discount rate.
P‘ and (2) the logarithms of the deviations of commercial interest rates from bond yields.
Our Unstable Dollar and the So-Called Business Cycle, Journal of the American Statistical Association, June, 1925, pp. 179-202.
The Loan Fund presented to the faculty of Harvard University in 1926-1927.
Part IV, Chapter 20
