The Theory of Interest
By Irving Fisher
THE tremendous expansion of credit during and since the World War to finance military operations as well as post-war reparations, reconstruction, and the rebuilding of industry and trade has brought the problems of capitalism and the nature and origin of interest home afresh to the minds of business men as well as to economists. This book is addressed, therefore, to financial and industrial leaders, as well as to professors and students of economics.Inflation during and since the War caused prices to soar and real interest rates to sag in Germany and other nations far below zero thus impoverishing millions of investors. In all countries gilt-edge securities with fixed return became highly speculative, because of the effect of monetary fluctuations on real interest rates. After the War the impatience of whole peoples to anticipate future income by borrowing to spend, coupled with the opportunity to get large returns from investments, raised interest rates and kept them high. Increased national income has made the United States a lender nation. At home, real incomes have grown amazingly because of the new scientific, industrial, and agricultural revolutions. Interest rates have declined somewhat since 1920, but are still high because the returns upon investments remain high. Impatience to spend has been exemplified by the organization of consumers’ credit in the form of finance companies specially organized to accommodate and stimulate installment selling and to standardize and stabilize consumption…. [From the Preface]
First Pub. Date
1930
Publisher
New York: The Macmillan Co.
Pub. Date
1930
Comments
1st edition.
Copyright
The text of this edition is in the public domain.
- Dedication
- Errata
- Preface
- Suggestions to Readers
- Part I, Chapter 1
- Part I, Chapter 2
- Part I, Chapter 3
- Part II, Chapter 4
- Part II, Chapter 5
- Part II, Chapter 6
- Part II, Chapter 7
- Part II, Chapter 8
- Part II, Chapter 9
- Part III, Chapter 10
- Part III, Chapter 11
- Part III, Chapter 12
- Part III, Chapter 13
- Part III, Chapter 14
- Part IV, Chapter 15
- Part IV, Chapter 16
- Part IV, Chapter 17
- Part IV, Chapter 18
- Part IV, Chapter 19
- Part IV, Chapter 20
- Part IV, Chapter 21
- Appendix to Chapter I
- Appendix to Chapter X
- Appendix to Chapter XII
- Appendix to Chapter XIII
- Appendix to Chapter XIX
- Appendix to Chapter XX
- Appendix to Chapter XX
§ 1 (to Ch. XII, § 1)
Algebraic expression of rate of time preference
APPENDIX TO CHAPTER XII
IF
W signifies wantability, or utility, or desirability and this year’s income is signified by
X‘ and next year’s by
X”, then
DW‘ may be taken to signify the present wantability of, or want for, a small increment,
DX‘ of money
this year and
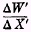 will be the want-for-one-more unit of money this year. Also
will be the want-for-one-more unit of money this year. Also
DW” is the present want for a small increment,
DX”, of money available
next year, and
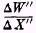 will be the present want-for-one-more unit of money available next year.
will be the present want-for-one-more unit of money available next year.
Exact mathematical theory requires that the marginal wants per unit of money are the
limits of those ratios when the increments approach zero as their limits or lim
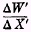 and lim
and lim
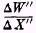 ordinarily written in the differential calculus:
ordinarily written in the differential calculus:
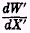 and
and
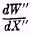 which, for short, may be called
which, for short, may be called
w‘ and
w”.
The rate of preference,
f, for a unit of present money over a unit of next year’s may be defined as
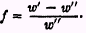
§2 (to Ch. XII,§3)
Equality of marginal rate of time preference and rate of interest implies that desirability of income stream is made a maximum
ASSUME at first that only two years are considered. The fact that total desirability or wantability of the individual, as reckoned at the beginning, depends on the amount of income this year and next year may be represented by the equation
c‘ +
x‘,
c” +
x”),
where
W” represents his total wantability, and the equation represents this
W” as a function of his income stream consisting of
c‘ +
x‘ this year and
c” +
x” next year. This
W” is represented in Chapters X and XI by the numbers attached to the several Willingness or Wantability lines, each representing a certain level of wantability of Individual
1. But as we shall here consider only one individual, we omit the subscript numbers, 1, 2,…,
n. The individual under consideration will attempt to adjust
x‘ and
x” so as to maximize
W. We are to prove algebraically that the condition that
W shall be a maximum implies also that the rate of interest
i shall be equal to the individual’s rate of preference
f. The condition
*2 that
W shall be a maximum is that the total differential of
W or of its equal F(
c‘ +
x‘,
c” +
x”), called below F( ) shall be zero; thus
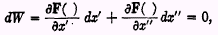
where the ∂’s represent the partial differentials with respect to
x‘ and
x”.
From this equation it follows that
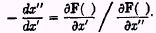
The
left-hand number of this equation is 1 +
i, as may be seen by differentiating the equation of the loan as originally stated, viz.:
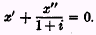 This differentiation yields
This differentiation yields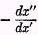 = 1 +
= 1 +i.
The
right-hand member, being the ratio of this year’s marginal wantability to next year’s marginal wantability, is by definition equal to 1 +
f. Substituting the new value for the right- and left-hand members, we have
i = 1 +
f,
whence it follows that
i =
f, which was to have been proved.
The same reasoning may now be applied to three or more years. The total wantability for any individual is a function of the total future income stream. In other words,
c‘ +
x‘,
c” +
x”,…,
c(
m) +
x(
m)).
The individual tries to make this magnitude a maximum. In terms of the calculus, this is equivalent to making the first total differential equal to zero namely,
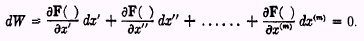
This total differential equation is equivalent, according to well-known principles of the calculus to a number of subsidiary equations obtained by making particular suppositions as to the different variations. Let us, for instance, suppose that only
x‘ and
x” vary in relation to each other and that
x”’,
xiv,…,
x(
m) do not vary. Then in the above equation all terms after the second disappear and the equation reduces, as before, to
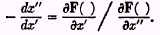
So that, again, 1 +
i‘ = 1 +
f‘, and therefore
i‘ =
f‘.
This expresses the relation between the first and second years. If we wish, in like manner, to express the corresponding connection between the second and third years, let us assume that
x‘ as well as
xiv,…,
x(
m) are constant but that
x” and
x”’ vary. Then the first term of the equation and all after the third disappear, and the equation reduces to
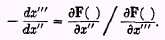
In other words, 1 +
i” = 1 +
f”, or
i” =
f”. Similarly,
i =
f for every other pair of successive years.
We have here, in mathematical language, the reason that the point of maximum total wantability is also the point at which the marginal rate of time preference for a unit of each year’s income over that of next year’s income is equal to the rate of interest connecting these two years.
*3
Advanced Calculus. Boston, Ginn & Co., 1912, pp. 118-125.
total wantability
W is vitally related to the function F in Chapters XII and XIII, representing the marginal rate of time preference
f, since 1 +
f is the ratio of the differential quotient of
W relatively to this year’s income to the corresponding differential quotient for next year’s income.
Appendix to Chapter 13
