The Theory of Interest

PART II, CHAPTER VI
SECOND APPROXIMATION TO THE THEORY OF INTEREST
Assuming Income Modifiable (1) by loans and (2) by other means

§1. The New Hypothesis

HITHERTO we have assumed:

(1) perfect foresight, and
(2) absence of any opportunity to alter income save by trading.

We now abandon the second of these hypotheses. Still assuming that all available income streams can be definitely foreseen, we now introduce the new hypothesis, much nearer actual life, that the income streams are not rigid, but are flexible, that is, that the owner of any item of capital-wealth or capital property, including, of course and especially, his own person, is not restricted to a sole use to which he may put it, but has open to his choice several possible or alternative uses, each of which will produce a separate optional income stream. He has, therefore, two kinds of choice: first, the choosing one from many optional income streams, and secondly, as under the first approximation, the choosing of the most desirable time shape of his income stream by exchanging present income against future.

The two sorts of choice are exercised concurrently in practice and each in consideration of the other. But, for purposes of exposition, we may take one at a time. Or rather, we may suppose the double choice made and then, in order to analyze it, we go back and consider each process separately, assuming the other constant. Let the varying process be the loan, that is, let us suppose one individual to have irrevocably made his choice from among options mutually available. This done, he is limited, as in the first hypothesis, to buying and selling or borrowing and lending as a means of changing the shape of that particular income stream. In this process he cannot change the present value, but in making his initial choice he had the privilege of selecting that option having the maximum present value.

For example, the owner of a piece of land may use it in any one of several different ways. He may, let us say, use it to grow crops, graze animals, plant forests, extract minerals, or to support buildings. Again, the owner of a building may use it, say, for office purposes, apartments, manufacturing, salesrooms, or a warehouse. Most raw materials, too, may be used for any one of a number of purposes. Iron may be wrought into steel rails, or into machinery, implements, tools, armor for ships, or girders for buildings. And so of tools and other implements; a derrick may be used for quarrying stone, building a house, or unloading a boat. A ship may be used to carry any sort of cargo, and sent over any one of numerous different routes. Hammers, saws, nails, and other tools may be used in almost numberless ways.

Perhaps the most adaptable of all instruments of wealth is man himself. He may be simply a passive enjoyer or "transformer"*55 of the services of other wealth and as such derive his satisfactions in any one or more of several different ways, sensual, esthetic, intellectual, or spiritual. Or, he may also be an active producer, and, as such, perform work in any one or more of several different ways, physical or mental. Even the skilled laborer who is most specialized and restricted has many ways to turn. And each of these varieties includes numerous sub-varieties. If his work is physical, it may consist in anything from wielding a pick and shovel to the deft manipulation of the instruments employed in the jeweler's art. If his work is mental, he may be a bookkeeper, clerk, superintendent, manager, director, lawyer, physician, clergyman, editor, teacher, or scientist. Some of these options, of course, may be out of the question and, in each case, there will be only one best choice. That choice is what is now under discussion.

In consequence of such a range of choice, any given productive instrument, or any given set of productive instruments, including human beings, may produce any one of many different income streams. Men may work to produce cheap frame houses or durable stone ones; to equip a city with trolleys, elevated, or under-ground rapid transit; to secure an income stream which shall consist of the pleasures of the table, of the amusements of the theatre, of the gratification of social vanities, or of endless combinations of these groups, as well as of all others. Each individual must select one particular income stream out of a thousand possible income streams differing in size, composition, time shape, and uncertainty; but, in this chapter, the element of uncertainty is, as already stated, supposed absent, being reserved for the third approximation (Chapter IX).

As in the first approximation, a perfect market is assumed in which each individual is so insignificant a part that he acts as if the market rate of interest were fixed and merely has to decide how much at that rate he is willing to borrow or lend.

Because of the existence of a wide range of choice, the owner of a given capital has ample opportunity to modify the income stream he derives from it by changing the uses to which that capital is put. He is seldom so committed to a definite future program but that he can consider some alternative. It is on this principle that the cotton belt of the United States, by diversifying its crops and industries, has increased its real income. The production of these Southern States has recently risen with expanding industries, diversified agriculture, water power development, and improved highways. It was largely by changing the uses to which its income, natural resources, and technological equipment had been put that the South has entered a new era.

Under the first approximation, our first glimpse of any flexibility of income was by borrowing and lending. Next we introduced the process of buying or selling and noted that this really included as a special case borrowing and lending. It might be claimed here that, just as buying and selling virtually include borrowing and lending, so the substitution of one use of a person's capital for another use may be said to include buying and selling, and therefore also to include borrowing and lending. It is evidently quite possible to say that one method of utilizing capital is to sell it. In fact, a merchant regards himself as making use of his stock in trade only in the sense of selling it.

While we could thus extend the meaning of optional uses to include buying and selling (which in turn include borrowing and lending) it will better serve the purpose of our analysis not to do so.

There are two principal reasons for this. First, borrowing and lending, the narrower method of modifying income streams, cannot be applied to society as a whole, since there is no one outside to trade with; and yet society does have opportunities radically to change the character of its income stream by changing the employment of its capital. Secondly, when borrowing and lending, or ordinary buying and selling, are employed to modify an income stream, the present value of the original income stream and the present value of the modified income stream are the same, for each $100 added to this year's income has the same present value as the $100 with interest, returned out of next year's income, so that every loan adds and subtracts equal present values. But when an income stream is modified by a change in the use of capital yielding it, the present value of the alternative, as in the case of the South, may not, and, in general, will not, be the same as the present value of the original. This fact, that the present value is not changed by buying or selling (or, in particular, by borrowing or lending) but is changed by otherwise altering the use of one's capital, marks an important distinction between the two methods of altering one's income stream. The distinction and its importance are most clearly seen by a mathematical analysis such as that shown in Chapter XI and XIII.

§2. Optional Income Streams

The choice among all available optional income streams will fall on that one which has the maximum desirability or wantability.

We have seen in the preceding chapter that income streams may differ in size, time shape, composition and certainty. As among income streams of different sizes but similar in other respects, the most desirable will, of course, be the largest.

As among income streams of different composition but similar in other respects, the most desirable will be that in which, to the given individual, the marginal desirabilities of the different constituents are proportional to their several prices, in accordance with the fundamental principle of marginal desirability in the theory of prices.*56

Finally, and principally, as among income streams differing in time shape alone, the most desirable is found in accordance with the principles which govern the rate of interest, and which are to be expounded in this book. It is, therefore, with income streams differing in time shape that we are here chiefly concerned.

In order definitely to illustrate income streams differing in time shape, let us begin by supposing only three. An individual is, let us say, possessed of a piece of land almost equally good for farming, lumbering, or mining. These terms are used merely to fix the reader's thought in concrete pictures. Logically, it would be better to designate the three optional supposititious income streams simply by the letters A, B, and C, for there is no pretense that the income streams closely resemble in more than a very general and sketchy way those of actual farming, lumbering, or mining; nor is it essential that the three products should differ in kind. Thus, the three streams might represent three different methods of producing the same product, one more roundabout or capitalistic than another. They are here given the concrete names of farming, lumbering, mining, merely for convenience in distinguishing and remembering the three types, not because these types are true to these names, nor because examples concerned with land comprise opportunities any more important than those concerned with commercial or industrial examples. The only essential point is that the three series of numbers representing the income streams A, B, and C are different.

Our imaginary land owner thus has the option of securing any one of these three different income streams. While they will, in the first instance, differ in composition—one income stream consisting in the production of crops, another in the production of lumber, and the third in the production of minerals—we may, for our present purpose, assume that these are all reduced to real income measured in terms of money. That is, we here assume that the prices and values of the crops, lumber, and minerals are given and determined in accordance with the principles which determine prices.*57

Assuming, then, that the land owner finds predetermined prices and quantities of crops, lumber and minerals, with predetermined costs for obtaining them, he has before him simply the choice of three definite income streams, each expressible in terms of money, according as he uses his labor, land, and capital in one or the other of the following three ways:

(1) for farming purposes, which, let us say, will give him a regular and perpetual succession of crops and income equally valuable year after year, that is, with an income stream of the type AA' in Chart 14;

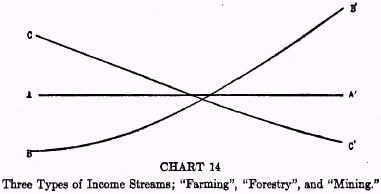
(2) for forestry purposes, with very slight returns for the first few decades, and larger returns in the future, as indicated by the curve BB';

(3) for mining purposes, in which case we shall suppose that the income is greatest for the early years and thereafter gradually decreases until the mine is exhausted; illustrated by Curve CC'.

The important question now before us is: What are the principles upon which the owner of the land chooses the best one among these three income streams, A, B, and C? This question is fundamental and typical in the second approximation.

The rate of interest is just as relevant to this initial choice of uses for maximum present value as to the subsequent choice for shape alone, for it is used in finding the present value; and when the rate changes, the relative present values of differently shaped streams may change about.

We shall suppose, as heretofore, that there is a uniform rate of interest in the community and that any individual is free either to borrow or to lend at that rate and up to any amount desired. Under this hypothesis the choice among the three available options will simply fall on that one which yields the maximum present value, reckoned at the market rate of interest.

Let us assume a market rate of interest at five per cent. To reckon the three respective present values, suppose the use of the land for mining purposes will yield an income stream, let us say, as follows: $2000 the first year, $1800 the second, $1600 the third, and so on, diminishing annually by $200 to the point of the mine's exhaustion. The present value of these ten sums, discounted at five per cent, is $9110. If the land is used for farming purposes and yields a net income of $450 a year perpetually, the present value at five per cent will be $9000. If, finally, the land is used for forestry purposes, we shall suppose it yields the following sums: zero for the first two years, $300 for the third, $400 for the fourth, $500 for the fifth, and $500 thereafter forever—then the value of the land, reckoning at 5 per cent, will be $8820.

Under these conditions the choice will evidently fall on the mining use, because, for mining purposes, the land is worth $9110, which is greater than $9000, its value for farming purposes, and than $8820, its value for forestry purposes.

The three options may be contrasted as to distribution in time as follows:

TABLE 2 The Three Optional Income Streams
	A For farming	B For forestry	C For mining
1st yr.	$ 450	$ 000	$2000
2nd yr.	450	000	1800
3rd yr.	450	300	1600
4th yr.	450	400	1400
5th yr.	450	500	1200
6th yr.	450	500	1000
7th yr.	450	500	800
8th yr.	450	500	600
9th yr.	450	500	400
10th yr.	450	500	200
11th yr.	450	500	000
	etc.	etc.	etc.
Present Value	$9000	$8820	$9110

The particular income stream selected will tend to leave its impress on the time shape of the total income stream of the individual who owns it. For, as was seen in Chapter I, the total net, or final, income stream of any individual during any interval of time is simply the sum total of the items of income flowing during that interval from all the articles of property belonging to him. Hence, if one selects the mining use for his land, whereby the income stream gradually decreases, its tendency will be to produce a similarly decreasing trend in the total income stream enjoyed by the individual. This tendency may be counteracted, of course, by some opposing tendency, but will have full sway if the income from all other capital than the land remains the same in value and time shape. It is true that the direct income from the mine is not itself real income, but consists of services which, relatively to some other capital source, are disservices, thus constituting intermediate income or interactions. But those items are readily transformed, through a chain of credits and debits, into real, and then into enjoyment income. Thus the ore of the mine is exchanged for money, and the money spent for enjoyable services or for commodities which soon yield enjoyable services, so that the real income closely copies in time shape *58 the original intermediate income from the mine.

§3. The Two Kinds of Choice

The possessor of the mine, however, is not compelled thus to copy in his real income the mine's fluctuations of physical or natural income. He may counteract any fluctuations in his whole net income which may be caused, in the first instance, by the choice of income C rather than B, or A. Or, if he prefers, he may further exaggerate those fluctuations. In fact he may make the time shape of his income follow any model he likes. He may do this as described under the first approximation, by either borrowing or lending in suitable amounts and at suitable times along his income stream; or, more generally, by buying and selling income streams or parts of income streams so as to fashion the time shape of his own final net enjoyable income to suit himself.

He may, for instance, so far as time shape is concerned, achieve an even flow of income such as he could get from the farm use of his land. But he will not on that account choose this farm use in preference to the mining use; for the mining use has the larger present value, and the undesirable time shape of its income stream, under our present hypothesis, can be very easily remedied. For instance, he may lend some of the proceeds of its earlier output and in later years be paid back with interest.

Of course, his loan at five per cent does not alter in the least the figure $9110, the discounted value at five per cent of all the ten items of income ($2000, $1800, $1600, $1400, $1200, $1000, $800, $600, $400, $200); it simply adds to the later of these ten figures and subtracts from the earlier ones. The present value of the additions is necessarily equal to the present value of the subtractions; for the additions are the repayments, while the subtractions are the loans, and the present value of any loan equals that of its repayment.

We may totally separate, therefore, in thought the two choices made by the land owner, namely, (1) the choice of C (mining) in preference to A and B on the ground of greater present value, and, (2) the choice of time shape. If, as just supposed for illustration, the second sort of choice is that of an even income stream, it will be at the rate of $455.50 a year perpetually. That is to say, the mine owner will lend at interest $1544.50 the first year (all but $455.50 out of his original mining income of $2000); in the second year he will lend $1344.50 (all but $455.50 out of his original $1800); and so on. When the ninth year is reached, he ceases to lend further, for the mine then yields only $400. Instead, he then ekes this out by $55.50 returned from the previous loans. Likewise, in the tenth year he ekes out the $200 from mining by $255.50 returned from loans. Thereafter he will get nothing further from mining; but his loans will have accumulated a sinking fund (of $9110) to take the place of the mine and from this fund he can annually derive a 5 per cent revenue of $455.50. Consequently, the net result of the double choice (mining use and even time shape) is to increase the perpetual income of $450 offered by farming to a perpetual income of $455.50. This new perpetual annuity has exactly the same time shape as that derived from the farming use, but is larger by $5.50 per annum.

Incidentally it may be observed that this mining income, thus evened out by financing into a uniform $455.50 per year, exceeds the uniform farming income of $450 in exactly the same ratio as the present value ($9110) of the mining income exceeds that ($9000) of the farming income.

The following table exhibits the operations in detail:

TABLE 3 Mining and Farming Use Compared
	Owner Receives from Mine	Of which He Lends	Leaving for Real Income	As Against Which the Farming Use Would Have Yielded
1st year	$2000	$1544.50	$455.50	$450
2nd year	1800	1344.50	455.50	450
3rd year	1600	1144.50	455.50	450
4th year	1400	944.50	455.50	450
5th year	1200	744.50	455.50	450
6th year	1000	544.50	455.50	450
7th year	800	344.50	455.50	450
8th year	600	144.50	455.50	450
9th year	400	-55.50	455.50	450
10th year	200	-255.50	455.50	450
11th year	000	-455.50	455.50	450
etc.	etc.	etc.	etc.	etc.

Or, instead of wanting a perpetual even flowing income, the land owner may prefer as his model the time shape of the forestry income. He will not, however, on that account, choose this forestry use in preference to the mining use. He will simply lend at interest from the items of mining income all of his $2000 the first year, leaving no income for that year; likewise, all of his $1800 the second; all but $310 the third; all but $413 the fourth and all but $516 the fifth, and every succeeding year until the ninth year. He will then turn around and use $116 from his loans just described to eke out his $400 and bring up his income in that year to $516. The tenth mining item, $200, will likewise be brought up to $516 after which he will depend entirely on his outside loans at five per cent, deriving therefrom exactly $516 every year.

The result will then be a series of income items exactly similar to the B, or forestry, series but each item magnified in the ratio of $9110 to $8820, the present values respectively of C and B.

The following table exhibits these operations:

TABLE 4 Mining and Forestry Use Compared
	Owner Receives from Mine	Of Which He Lends	Leaving for Real Income	As Against Which the Forestry Use Would Have Yielded
1st year	$2000	$2000	$000	$000
2nd year	1800	1800	000	000
3rd year	1600	1290	310	300
4th year	1400	987	413	400
5th year	1200	684	516	500
6th year	1000	484	516	500
7th year	800	284	516	500
8th year	600	84	516	500
9th year	400	-116	516	500
10th year	200	-316	516	500
11th year	000	-516	516	500
etc.	etc.	etc.	etc.	etc.

Since, therefore, any time shape may be transformed into any other time shape, nobody need be deterred from selecting an income because of its time shape, but everyone may choose an income exclusively on the basis of maximum present value. It will then happen that his income, as finally transformed, will be larger than it would have been if he had chosen some other use which afforded that same time shape.

All this is true under the assumption used throughout this chapter, namely, that after the most valuable option has been chosen, you can borrow and lend or buy and sell ad libitum and without risk. If this assumption is not true, if a person were cut off from a free loan market, the choice among optional income streams might or might not fall upon that one having the maximum present value, depending on the other circumstances involved, particularly his preferences as regards time shape.

Of course our assumption is a violent one, made in this second approximation, as in the first, in order to simplify the theory of interest. But already it must be evident that the principle involved has important practical applications. To a very considerable extent a modern business man, with access to loan markets, can choose from among the various options open to him on the basis of present value, and trust to loans or other financing to rectify any inconvenience in time shape.

The lines AB and A'B' in Chart 15 picture alternative income streams, of which the descending one, AB, has the larger present value. The choice will fall on AB, and if the individual prefers the time shape of A'B', he will then lend some of the early receipts from the income stream AB and receive back some of the latter, converting his income AB of undesirable shape into the income stream A''B'' which has the desired shape. This final income A''B'' combines the virtues of both the original alternative incomes AB and of A'B'; it possesses the superior shape of A'B' and the superior present value of AB. As compared with A'B' it has the same shape but a greater size.

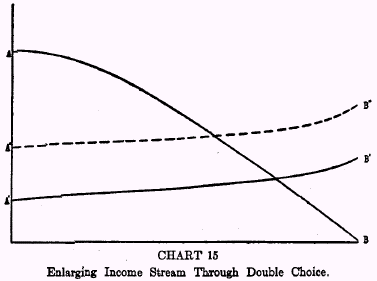
In practice, of course, the two steps are usually made simultaneously, not successively. In fact, usually the borrowing or financing often precedes the choice of option, thus reversing the order of presentation here adopted for convenience of exposition. So it would be quite as true to say that the loan, with the choice of option it makes possible, is made to secure an increased income as it is to say that the loan is made to even up the distorted income given by the option chosen.

But were it not for the possibility here assumed of modifying the time shape of his income stream by borrowing and lending, or buying and selling, the land owner would not feel free to choose the one from among the optional income streams which possesed the highest present value. He might find it advantageous, or even necessary, to take one of the others, being scarcely able to live if his property offered only distant income. If his capital were all in the form of growing young forests, and he could not mortgage the future in some way, he would have to starve or give up some of his holdings. In actual life we find such people—people who are said to be "land poor." In fact, we are all somewhat hampered in the choice of options by difficulties and risks both in the choice of options and in the financing it requires.

But we see that, in such a fluid world of options as we are here assuming, the capitalist reaches his final income through the co-operation of two kinds of choice of incomes which, under our assumptions, may be considered and treated as entirely separate. To repeat, these two kinds of choice are: first, the choice from among many possible income streams of that particular income stream which has the highest present value, and, secondly, the choice among different possible modifications of this income stream by borrowing and lending or buying and selling. The first is a selection from among income streams of differing market values, and the second, a selection from among income streams of the same market value.

§4. Opportunity to Invest by Change of Use of Capital

Since this double choice results, when made, in a perfectly definite income stream, it might seem that the situation does not materially differ from the case of the rigid income stream discussed in the first approximation. But the two cases do differ materially, for under the present hypothesis (of optional income streams) the particular choice made by the individual depends upon what the rate of interest is. A change in that rate may shift the maximum present value to some other option, or alternative income stream, and that shift reacts on the rate of interest.

In the example cited, if the rate of interest should be 4½ per cent instead of 5 per cent, the order of choice would be changed. The present value of the land for A (farming) would be $10,000, for B (forestry), $9920, and for C (mining), $9280. The farming use, or A, would now be the best choice. Again, if the rate of interest should be 4 per cent instead of 4½ per cent, the present value of the use of the land for A, farming purposes, would be $11,250; for B, forestry purposes, $11,300; and for C, mining purposes, $9450. In this case, B, the forestry use, would be chosen.

Thus, it would pay best to employ the land for mining if the rate of interest were 5 per cent, for farming if it were 4½ per cent, and for forestry if it were 4 per cent.

The three options open to the owner of the land at these three different rates of interest may be summarized as follows:

TABLE 5 Present Values of the Three Options at Three Different Rates of Interest
Options	Present Value at
	5%	4½%	4%
For forestry	$8,820	$ 9,920	$11,300
For farming	9,000	10,000	11,250
For mining	9,110	9,280	9,450

Thus a change in the rate of interest results in a change in the relative attractiveness of different optional income stream opportunities. A high rate of interest will encourage investment in the quickly returning incomes, whereas a low rate of interest will encourage investment in incomes which yield distant returns. As the business man puts it, when interest is high, he can less afford to wait for a remote return because he will "lose so much interest." An investor will, therefore, make very different choices among the various options open to him, according as interest is at one rate or another.

Consequently, the existence of various options to use one's capital introduces a new variable into the problem of interest determination. For the individual, the rate of interest will determine the choice among his optional income streams, but, for society as a whole, the order of cause and effect is reversed—the rate of interest will be influenced by the range of options open to choice. If we live in a land covered with young forests or otherwise affording plenty of opportunities for distant income but affording few opportunities for immediate income (as was the case in the pioneer days in this country) the rate of interest will, other things being equal, be very much higher than in a land full of nearly worked out mines and oil fields or otherwise affording many opportunities for immediate but few opportunities for remote income.

We are thus coming in sight of a principle, applying to interest determination, new in our study, the principle of opportunity to invest, not simply by lending but by changing the use of one's capital. This new principle, largely physical or technical, is just as important as the psychical principle of human impatience. It is really old in the sense that, implicitly, it has been recognized in almost all theories of interest, and explicitly in those of Rae, Landry, Walras, and Pareto. To trace this new influence on interest is the special purpose of the second approximation.

§5. The Reasoning not "Circular"

At first sight it may appear to those not familiar with the mathematics of simultaneous equations and variables that the reasoning is circular; the rate of interest depends on individual rates of impatience; these rates of impatience depend on the time shapes of individual income streams; and the choice of these time shapes of income streams depends, as we have just seen, on the rate of interest itself.

It is perfectly true that, in this statement, the rate of interest depends in part on a chain of factors which finally depend in part on the rate of interest. Yet this chain is not the vicious circle it seems, for the last step in the circle is not the inverse of the first.

To distinguish between a true and a seeming example of a circular dependence we may cite simple problems in algebra or mental arithmetic. Suppose we wish to find the height of a father who is known to be three times as tall as his child. To solve this we need to know something more about these two heights. If we are told in addition that the child's height differs from his father's by twice itself, the problem is really circular and insoluble, for the additional condition is really reducible to the first, being merely a thinly veiled inversion of it. The problem essentially states (1) that the father's height is three times the child's and (2) that the child's is one-third of the father's—an obvious circle.

But if the dependence of the father's height on the child's is essentially different from—independent of—the dependence of the child's on its father's, there is no circle. Thus supposing, as before, that the father is three times as tall as the child, let us stipulate in addition that the child's height differs from the father's by four times as much as the child's less two feet. This may sound as circular as the first statement—the father's height is expressed in terms of the child's, and the child's is expressed in terms of the father's; but the second stipulation is not now reducible to the first. The heights are entirely determinate, that of the father being six feet and that of the child, two. The mere fact that both of these magnitudes, the father's height and the child's height, are specified each in terms of the other does not constitute a vicious circle. The general principle, as Cournot and other mathematical economists have often pointed out, is simply the well known algebraic principle of simultaneous equations. In order that the equations may determine the unknown quantities involved, there must be as many independent equations as there are unknown quantities, although any or all of these equations may contain all the unknowns. (The equations are independent if no one of them can be derived from another or the others.) Many an example of economic confusion and wrong reasoning could be avoided if this fundamental principle of mathematics were more generally applied.

This mathematical principle of determinateness applies in our present problem. Real examples of circular reasoning in the theory of interest are common enough, but the dependence, above stated, of interest on the range of options and the dependence of the choice among them on interest is not a case in point, for this last determining condition is not derivable from the others.*59

For our present purpose we need only present the matter to the reader's imagination by a process of trial and error. To find the rate of interest on which the market will finally settle, let us try successively a number of different rates. First, let us suppose a rate of 5 per cent. This rate will determine the choice between options for each individual. The land owner formerly supposed will, as we have seen, choose C, the mining use, because the present value of the income so obtained ($9110) exceeds the present values of the rival uses. Every other individual in the market, in like manner, will select that particular use for his capital which will give him the maximum present worth. With these choices made, the different individuals will then enter the market of loans or sales, desiring to modify the time shapes of their income streams to suit their particular desires.

As a result of all these choices, the total amount which all the would-be lenders are willing to lend at 5 per cent out of this year's instalment of their chosen income stream will be perfectly definite, and likewise the total amount which all the would-be borrowers are willing to take. This we saw in the preceding chapter. In other words, the demand and supply of loans for the present year, at the given rate of interest, 5 per cent, will both be definite quantities. Should it happen that the supply of loans exceeds the demand, it would follow that 5 per cent could not be the correct solution of the rate of interest, for it would be too high to clear the market.

In that case, let us try again; suppose a rate of 4 per cent. Following the same reasoning as before, we now find that the land owner will select the forestry opportunity for his land because the present value ($11,300) of the income from forestry—now reckoned at 4 per cent—will exceed that of the two rival income possibilities. Other capitalists will likewise select their best option from among those available to them and on the basis of these income streams—not the same as before under 5 per cent. In a word, there will now be a different supply and demand. The land owner, for instance, instead of lending, may now borrow (or sell securities) to even up his income stream. Should it then happen that the demand and supply of loans, on the basis of 4 per cent, are still not equal, but that, this time, the demand exceeds the supply, it would be a proof that not 4 per cent is the true solution, but some higher rate. By again changing our trial rate—part way back toward 5 per cent, we may evidently reach some intermediate point, let us say 4½ per cent, at which rate not only will each individual choose the best use of his capital—that having the highest present worth—but also, at the same time, the demand and supply of loans engendered by all such choices will exactly clear the market, i.e., bids and offers at the given rate will be equal. Likewise, the same clearing will be worked out for next year and for all years.*60

The introduction, therefore, of flexibility into our income stream still leaves the rate of interest entirely determinate, even though the income streams are now, in the second approximation, not fixed or rigid but subject to choice, and even though that choice will depend on the rate of interest itself.

§6. Summary

For the determination of the rate of interest we must now, therefore, in the second approximation, add two new principles to the four principles already given in the first approximation described in the previous chapter.

THE TWO INVESTMENT OPPORTUNITY PRINCIPLES

A. Empirical Principle

There exists, for each individual, a given specific set or list of optional income streams to choose from, differing in size and time shape (but without any uncertainty as to what will happen if any particular one is chosen).

B. Principle of Maximum Present Worth

Out of this list of options each individual will choose that particular income stream possessing the greatest present worth when calculated by means of the rate of interest as finally determined by these six conditions.

THE TWO IMPATIENCE PRINCIPLES

A. Empirical Principle

The degree of impatience, or rate of time preference, of any given individual depends upon his income stream as chosen by him and as modified by exchange.

B. Principle of Maximum Desirability

Each person, after or while first choosing the option of greatest present worth, will then modify it by exchange so as to convert it into that particular form most wanted by him.

This implies, as we have seen, that each person's degree of impatience, or rate of time preference, will at the margin, be brought to equality with the market rate of interest and, therefore, with the marginal preference rates of all the other persons.

THE TWO MARKET PRINCIPLES

A. Principle of Clearing the Market

The rate of interest must be such as will clear the market, that is, equalize supply and demand. That is, for every time interval, the additions to some individuals' incomes caused by borrowing or selling must balance the deductions from others caused by lending or buying.

B. Principle of Repayment

The loans must be equivalent in present worth to repayments, or, more generally, the additions to any individual's income, brought about by borrowing or selling, in some time intervals must be equivalent in present worth to the deductions from his income in other time intervals brought about by lending or buying.

Thus we see that the rate of interest is determined by two principles of investment opportunity as well as by two principles of impatience and by the two self-evident market principles.

More briefly stated, the rate of interest is determined so as (1) to make the most of opportunities to invest, (2) to make the best adjustment for impatience and (3) to clear the market and repay debts.

In short, the theory is thus one of investment opportunity and human impatience, as well as exchange.

But while we have reached the two chief theoretical foundations of our subject, we are still, of course, far from the real world. The real world is vastly more complex than the imaginary world described in this chapter. In particular, we still need to take account of risk. This we shall do in the third approximation.