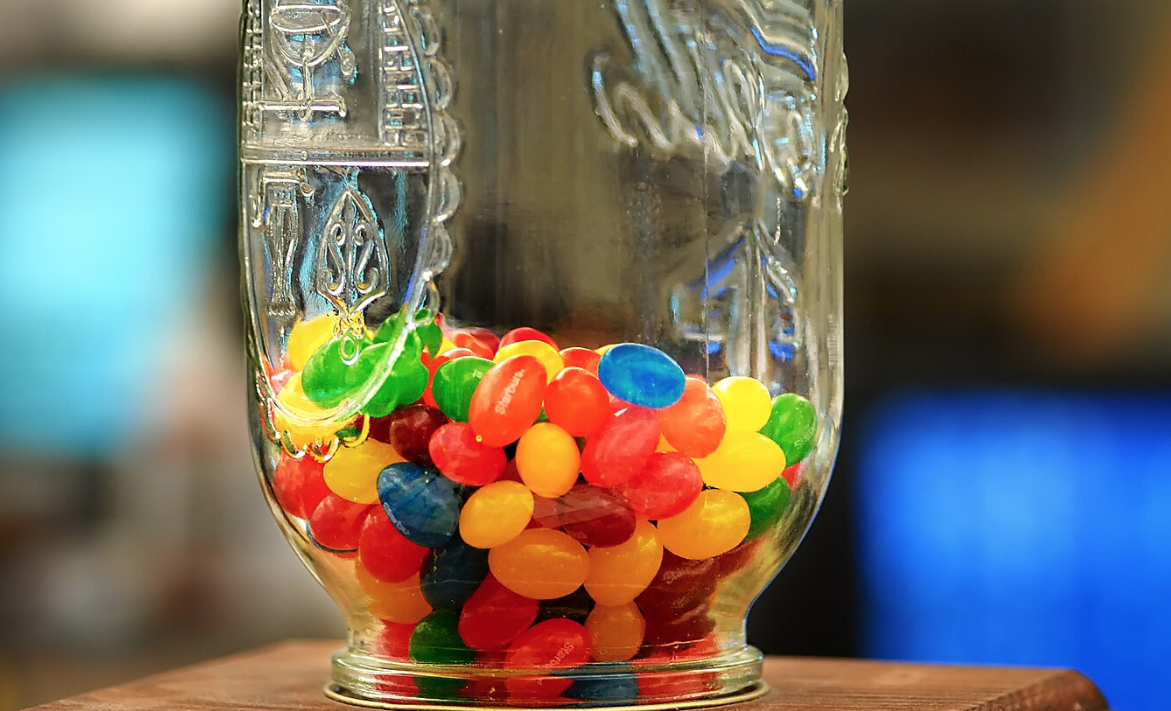
John Cochrane has an excellent post discussing Bob Lucas’s contributions to macroeconomics. Here’s a point that I also keep harping on:

The Fed often asks economists for advice, “should we raise the funds rate?” Post Lucas macroeconomists answer that this isn’t a well posed question. It’s like saying “should we cry wolf?” The right question is, should we start to follow a rule, a regime, should we create an institution, that regularly and reliably raises interest rates in a situation like the current one? Decisions do not live in isolation. They create expectations and reputations. Needless to say, this fundamental reality has not soaked in to policy institutions. And that answer (which I have tried at Fed advisory meetings) leads to glazed eyes. John Taylor’s rule has been making progress for 30 years trying to bridge that conceptual gap, with some success.  

Lucas is the economist that launched the rational expectations revolution.  Much of the skepticism about “rational expectations” comes from a lack of comprehension about what the assumption actually means. Here’s Cochrane:

But “rational expectations” is really just a humility condition. It says, don’t write models in which the predictions of the model are different from the expectations in the model. If you do, if your model is right, people will read the model and catch on, and the model won’t work anymore. Don’t assume you economist (or Fed chair) are so much less behavioral than the people in your model. Don’t base policy on an attempt to fool the little peasants over and over again. It does not say that people are big super rational calculating machines. It just says that they eventually catch on. 

I’d like to illustrate the issue with a hypothetical example involving a big glass jar of jellybeans. You may recall a famous example cited in the “wisdom of crowds” literature, where an MBA class was asked to estimate the number of jellybeans in a large jar. Most of the guesses were far from reality, but the median guess was surprisingly close, say within 1% or 2%. In that case, how would I model the public’s jellybean estimates? 

The least bad approach might be to estimate the actual number of jellybeans, and then assume that this figure was also the public’s estimate. This approach would not work perfectly, but it’s hard to see any alternative that would be better. Would you wish to assume the average guess is only 60% of the truth? How about 150%? If so, why?

Now suppose I ask a mathematician how many ellipsoids with dimensions of 9 mm long and 6 mm wide will fit into a cylinder that is 8 inches tall and has a diameter of 5 inches. The mathematician provides an equation that looks sort of complicated to the average person. Does it make sense to assume that the average person uses that equation when estimating the number of jellybeans? Obviously not. But that equation gives you a good estimate of the actual number of jellybeans, and if we have no reason to assume the public’s estimates are biased, then it also provides the best model of the public’s estimate.

Rational expectations models in macroeconomics are often full of scary looking equations. The modeler then assumes that the public’s forecast of variables such as inflation is “consistent” with the model. Thus if the model predicts 7% inflation, we don’t assume that the public forecasts 3% or 13% inflation—why would we? We assume that the public also expects 7% inflation. That may not be correct, but it seems the least bad approach unless we have specific knowledge that the public either over or under estimates the variable in question. (Unfortunately, this is hard to test, as inflation is poorly defined. The public’s estimates that show up in places like the Michigan survey probably reflect a definition of inflation that doesn’t include hedonic adjustments, and thus is a bit higher than the government inflation estimate.)

Many people reject rational expectations because it seems to suggest that the public is composed of super intelligent calculating machines. But that’s not at all what it means. Bennett McCallum suggested that it would have been better to call the concept “consistent expectations.” The claim is actually quite modest. All the rational expectations assumption says is that if your model specifically implies that X is true; don’t assume the public believes that X is false, at least not without evidence for that claim.