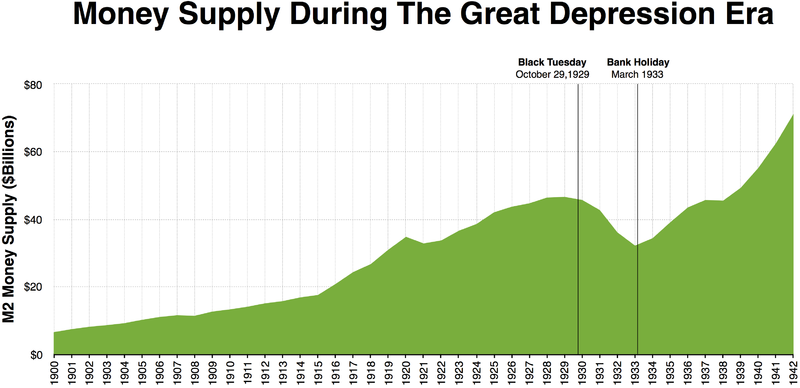
In Jeff Hummel’s Monetary Theory and Policy class recently, he assigned an interesting computational problem that shed light on the main factors driving the drop in the U.S. money supply between 1929 and 1933. He used a problem from Greg Mankiw’s Intermediate Macro text. The problem didn’t give magnitudes but I assume everything was in billions of dollars.
The money supply was $26.5 billion in 1929 and $19.0 billion in 1933. That’s a drop of 28 percent.
Here was the first question. What would have happened to the money supply in 1933 if the currency-deposit ratio had risen the way it did but the reserve-deposit ratio had remained constant? (The c/d ratio rose because people tried to convert their demand deposits to currency; the r/d ratio rose because banks were trying to have reserves available for people trying to convert their demand deposits to currency. Both factors caused the money supply to fall.)
M = (cr + 1)/(cr + rr) times B,
where M is the money supply,
B is the monetary base = currency held by the public (C) plus bank reserves (R)
cr is C/D, where D is demand deposits
rr is R/D.
In August 1929,
C = $3.9 billion
D = $22.6 billion
B = $7.1 billion
R = $3.2 billion.
To make sure the formula worked, I plugged the numbers in for August 1929.
cr = C/R = 3.9/22.6 = of 0.17
rr = R/D = 3.2/22.6 = 0.14.
So plug and chug.
M = (0.17 + 1)/(0.17 + 0.14) times 7.1
= 1.17/0.31 times 7.1
= 3.8 * 7.1
= 27.0 (close enough)
By 1933, cr had risen to 0.41 and rr had risen to 0.21.
So if rr had stayed at 0.14, the only other thing we need to know is B in 1933. That was $8.4 billion.
So M would have been (0.41 + 1)/(0.41 + 0.14) times 8.4
= 1.41/0.55 times 8.4
= $21.5 billion.
In other words, rather than falling from 26.5 to 19, the money supply would have fallen to 21.5.
Next question:
What would have happened to the money supply if the reserve–deposit ratio had risen but the currency–deposit ratio had remained the same?
R/D rose to 0.21. Assume C/D stays at 0.17.
Then M = (0.17 + 1)/(0.17 + 0.21) times 8.4
= 1.17/0.38 times 8.4
= 3.08 * 8.4
= $25.9 billion.
So the money supply would have fallen from 26.5 to 25.9, a drop of only 2.3 percent.
In part (c), which mattered more? The increase in the currency/deposit ratio.

READER COMMENTS
Matthias
Mar 22 2021 at 11:10am
If only banks had been allowed to print their own notes..
David Henderson
Mar 22 2021 at 12:28pm
Exactly. This theme has come up a number of times in the class.
Marc Herlands
Mar 22 2021 at 4:03pm
Friedman and Schwartz, and later Bernanke, focused our attention on the decline of the Money Supply as a significant cause of the Great Depression. Bernanke expanded our attention to include the Gold Standard. I wish to point out that raising short term interest rates by the Fed in 1928 and 1929, caused the Recession and the Stock Market to crumble. Thus began the Credit Crunch. Banks withdrew from lending to consumers, and prices for finished goods fell. Production of durable goods and housing fell. Unemployment rose swiftly. Consumption fell, and bankruptcies increased. As banks stoped making consumer, commercial and real estate loans and bankruptcies increased, Banks began to fail increasingly. By the end of 1930, faith in the financial stability of banks was reduced; depositors withdrew their funds, which decreased the money supply, and started saving more, which reduced velocity of money. England and it’s Commonwealth’s abandonment of the Gold Standard caused US exports to plummet. Sterling’s devaluation caused US Imports to rise, which put marginal US producers into bankruptcy. This downward spiral was halted only when the US had a banking holiday where banks were given Stress Tests, the Fed began to increase reserves, and the US abandoned the Gold Standard. There were more factors that caused the Great Depression than just a decline in the Money Supply.
Andrew_FL
Mar 23 2021 at 1:47pm
Focusing on the Gold Standard is quite literally a narrowing of our attention, not an expansion of it.
Comments are closed.