The Purchasing Power of Money

APPENDIX TO CHAPTER II

§ I (TO CHAPTER II, § 3)
The Concept of an Average

The subject of averages or means is so important—both theoretically and practically—and so little upon it is readily available for economic readers that a short statement of its fundamental principles may be fitly inserted here.*1

There are numerous kinds of averages or means. Among them are the arithmetical, geometrical, and harmonical; and of each of these there are many different varieties. The simple arithmetical mean of a specific series of terms is found by adding the terms together and dividing by their number. Thus, suppose it is desired to find a mean of 2 and 8. It is evidently

This is, as a matter of fact, the mean most commonly employed.

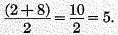
The simple geometrical mean is obtained by multiplying all the terms together and extracting that root of the product which corresponds to the number of terms. Thus, the geometrical mean of 2 and 8 is 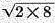or 4.

The simple harmonical mean of any number of terms is the reciprocal of the arithmetical average of their reciprocals. For 2 and 8 it is

or 3 1/5.

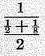
The weighted arithmetical mean is a modification of the simple arithmetical mean. Suppose it is desired to find the mean height of two groups of trees, one tall, the other short. The tall group is 8 yards high, the short, 2. The simple arithmetical mean as we have seen is 5. But this mean treats both groups as of equal importance. Let us suppose that there are twenty of the two-yard trees and ten of the eight-yard trees, and let us seek a mean of the two heights, such as will give equal importance to each tree. This will give the short group of twenty trees twice the importance of the tall group of ten trees. We shall be giving equal importance to each tree if we take the simple arithmetical mean of the thirty trees. But this simple mean of thirty trees will be a weighted mean of the two groups of trees. It is to be found by adding their heights together (twenty heights of two yards plus ten of eight) and dividing by the number of trees (20 + 10). That is, the mean height is

and this (considered as an average of the two groups instead of that of the thirty trees) is said to be the weighted arithmetical mean of 2 and 8, the 2 being weighted twenty times, and the 8, ten times. The weighted mean of the two groups means the simple mean of the thirty trees. In other words when we "weight" the various terms averaged, we no longer count these terms once each, but we count one term as though it were (say) twenty, and another as though it were (say) ten and the number of times we count a term is its "weight." In the same way we may define the weighted geometrical and weighted harmonical means. Taking the same example of the trees, we find the results to be respectively or 3.175 and

or 2 2/3.

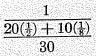
The same results would have been obtained in each case if, instead of the weights 20 and 10, we had taken, as weights, 2 and 1.

Since there are so many different kinds of means, the question arises, What is the meaning of an average or mean in general? We answer: Any mean of a series of terms must be obtainable from them by a mathematical rule such that, when applied to a series of identical terms, it will make their mean identical with each of them. Any rule of averaging is admissible which is consistent with this condition (that the average of identical terms must be identical with each). We know that the simple arithmetical mean A, of a, b, and c is

It is easy to see that this formula meets the required test. Substituting A for each of the three magnitudes a, b, and c in (a + b + c)/3, we obtain

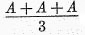
which is evidently equal to A; thus the test is satisfied.

Again, let G be the geometrical mean of a, b, and c; so that G = This formula also conforms to the definition of a mean because G = .

Similarly, the harmonical average (which we may call H) of a, b, and c is

This also conforms, because

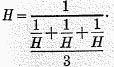
For a weighted arithmetical average A_w of a, b, c, the weights being a, b, g, we have the formula

which conforms to our test, since evidently

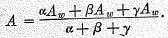
By applying this general rule, we can make at will innumerable kinds of averages. It is only necessary to write any formula twice, once using the terms to be averaged and once using, instead, the required average, and then equate the two. Thus, let us take the complicated formula

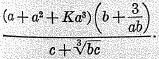
This may be employed to obtain a new species of average (x) of a, b, and c, simply by equating it with the similar form

That x as determined by this equation will conform to our definition of an average is evident, since substituting x for a, b, and c, the equation becomes a truism, showing that the proposed new average of the identical terms x is x.

A special case of the definition, requiring particular mention, is that in which two or more means (not necessarily of the same kind) are related to one another. In order that A should be a mean of a₁, a₂, a₃,...when we know that B is a mean of b₁, b₂, b₃,...it is only necessary to have a determining formula such that if a₁ = a₂ = a₃...and at the same time b₁ = b₂ = b₃...(each of which by hypothesis must be equal to B), then A shall also be equal to each of the magnitudes a₁, a₂, a₃, etc. Many examples of pairs of means like A and B will be given in Chapter X (on the construction of index numbers). The following is a simple example:—

Let nAB = a₁b₁ + a₂b₂ + a₃b₃ +...and let B be the arithmetical mean =

(n being the number of terms). Then A is a (new) sort of mean of a₁, a₂, a₃; for, substituting A for a₁, a₂, a₃,... and B for b₁, b₂, b₃, in the equation nAB = a₁b₁ +..., the equation is satisfied.

§ 2 (TO CHAPTER II, § 5)
The Concept of Velocity of Circulation

The velocity of circulation of money has been defined as a ratio of the money expended to the average money on hand, that is, as a rate of turnover. A rate of turnover differs from the popular concept of velocity. The latter regards velocity as the average number of times money changes hands from one person to another; whereas, the concept we have employed treats velocity as the average number of coins which pass through one man's hands, divided by the average amount held by him. The difference between the two concepts is very similar to that between two methods of obtaining the velocity of a railway train. One method is to follow the train for a certain number of miles, and note how long a time it takes to travel those miles. The other is to stand on a certain spot beside the track and note the time consumed by a given length of train in passing that spot. Following the train from place to place is like following a coin from person to person, while watching the train pass one point is like observing the rate of turnover of one person's purse. We may distinguish the two methods as the "coin-transfer" method and the "person-turnover" method. Both methods, if correctly employed, yield the same result. But in the coin-transfer method, an important distinction is usually overlooked, the distinction between the gross and net circulation of money. What is desired is the rate at which money is used for purchasing goods, not for "making change." The result is the difference between the number of times each piece changes hands against goods, and the number of times it changes hands with goods. If a $10 bill is transferred in purchase of goods and $2 is given back "in change," the actual money expended for goods is measured, not by $12, the gross transfer of money, nor yet by $10, the gross amount transferred against goods, but by $8, the net amount paid for goods.

If it is desired, in the coin-transfer method, to learn the average velocity of circulation of two pieces of money, such as a dollar and a ten-cent piece, we must not only find the net rate of turnover of each coin, but also take account of the discrepancy between the buying efficiencies of the two coins. Let it be assumed that during the year the dollar is passed 115 times against goods and 15 times with goods, so that its net velocity of circulation is 115 - 15 or 100. If we suppose the velocity of the ten-cent piece to be 290 - 90 or 200, the average velocity of the two must somehow take account of the different values of different denominations. A dollar is the equivalent of ten dimes. Its rapidity of circulation should therefore be "weighted" tenfold in order to get the real average, that is, the average of the service performed by the two. The net rate of circulation of 100 for the dollar is equivalent to a net velocity of circulation of 100 for each and every one of ten dimes. It follows that the average velocity of the two coins is

,

a result much closer to the velocity of the dollar than to that of the dime. With these two safeguards against error applied to the coin-transfer method, it is easy to see that the coin-transfer method will yield the same results as the person-turnover method.*2

There is yet another magnitude which should be considered in connection with the velocity of monetary circulation. This may be called the average time of turnover, i.e. the average amount of time consumed by all the given money, in being turned over once. This is the "reciprocal" of velocity. If money changes hands twenty times in a year, it turns over, on the average, once in 1/20 of a year, or once in somewhat over 18 days. This is its average time of turnover. If the average velocity of circulation or rate of turnover is forty times a year, then the average time of turnover is 1/40 of a year or about 9 days. Or, instead of considering all the given money directly, let us come at it through a component part of it. If a man having, on the average, $10 in his pocket every day, expends on the average $1 a day, he evidently turns over 1/10 of his money each day. Since to turn over 1/10 of his average stock each day is to turn over the whole of it 36½ times a year or once in 10 days, the time of turnover will be 10 days. If the man under consideration had a pocketbook arranged with a series of ten one dollar bills, and every day, as one was taken from the top to be expended, another were added at the bottom, evidently any and every bill would remain in his hands just ten days traveling from the bottom to the top of the pile.

§ 3 (TO CHAPTER II, § 5)
"Arrays" of p's, Q's, and pQ's

Let us assume that the year is divided into an indefinite number of periods, or moments, and distinguish the prices and quantities relating to those successive periods by the subscripts 1, 2, 3, etc., at the left; and that we are dealing with a community of an indefinite number of persons, distinguished likewise by subscripts at the right. Thus the quantity of a particular kind of goods purchased by individual No. 1 in moment No. 3 is represented by ₃q₁ and the price of the sale by ₃p₁. The entire system of quantities and prices is represented by the two following "arrays."

PERSONS	PERIODS			TOTAL	PERSONS	PERIODS			AVERAGE
	1	2	3			1	2	3
1	1q1	2q1	3q1	Q1	1	1p1	2p1	3p1	p1
2	1q2	2q2	3q2	Q2	2	1p2	2p2	3p2	p2
3	1q3	2q3	3q3	Q3	3	1p3	2p3	3p3	p3
—	—	—	—	—	—	—	—	—	—
—	—	—	—	—	—	—	—	—	—
Total	1Q	2Q	3Q	Q	Average	1p	2p	3p	p

We have just stated the meaning of the letters inside these arrays. Those outside are as follows: Q₁ is the total quantity bought by person 1 and is the sum (₁q₁ + ₂q₁ + ₃q₁ +...) of all quantities purchased by him in all the different periods of time. Like definitions apply to Q₂, Q₃, etc. ₁Q is the total quantity purchased in moment 1 and is the sum (₁q₁ + ₁q₂ + ₁q₃ +...) of all quantities purchased in that moment by all the different persons. Like definitions apply to ₂Q, ₃Q,.... Finally Q is (as already employed in the text) the grand total of quantities bought by all persons in all periods of time. Evidently,

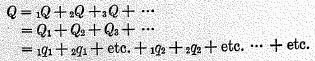
Like definitions apply to the letters outside the p array, but the relations to the letters inside are here averages instead of sums. We may best derive the form of these averages from a third or intermediate array for pQ indicating the money values of the purchases.

This last named array is

PERSONS	PERIODS			TOTAL
	1	2	3
1	1p11q1	2p12q1	3p13q1	p1Q1
2	1p21q2	2p22q2	3p23q2	p2Q2
3	1p31q3	2p32q3	3p33q3	p3Q3
Total	1p1Q	2p2Q	3p3Q	pQ

In this array the same relations must evidently hold as in the Q array. That is, pQ, the entire sum spent on the given commodity by all persons in the community during all periods of the year, must be equal to (1) the sum of the column above it, (2) the sum of the row at its left, and (3) the sum of the interior terms of the array. In other words, it must be equal to (1) the sum of the total yearly amounts spent by the many different persons, (2) the sum of the total amounts spent in the community at the many different periods of the year, and (3) the sum of the purchases of all the individuals in all the periods.

The nature of the p array is now determined by the Q and the pQ arrays. It must namely be such as to permit the summation just described for the pQ array. That is, each of the average prices (such as p₁) must conform to the type of formula:—

Hence, p is a weighted average of ₁p₁, ₂p₁, etc., the weights being ₁q₁, ₂q₁, etc. That is, the average price paid by person No. 1 is the weighted arithmetical average of the prices paid by him at different moments through the year, the weights being the quantities bought. The same principle obtains for all other persons.

Similarly, the average price, ₁p, may be shown to be

That is, the average price in period No. 1 is the weighted arithmetical average of all prices paid by different persons at moment No. 1, the weights being the quantities bought by each. The same principles obtain at all other moments.

Finally, the average price, p, in the lower right corner of the p array, is either

(that is, p is a weighted arithmetical average of p₁, p₂, etc., the weights being Q₁, Q₂, etc.; or (using the row instead of column), p is the like weighted arithmetical average of ₁p, ₂p, etc., the weights being ₁Q, ₂Q, etc.; or lastly, either of these two expressions for p, combined with the preceding expression for p₁, p₂, etc., or with that for ₁p, ₂p, etc., may be used to show that p is a weighted arithmetical average of all the p's within the array, the weights being the corresponding q's. In short, the price of each commodity for the year is its average at all times and for all purchases in the year weighted according to the quantities bought.

This principle covers the method of averaging prices in different localities. Thus the average price of sugar in 1909 in the United States is the weighted arithmetical average of all prices of sales by all individuals throughout the United States, and at all moments throughout the year, the weights being the quantities bought. Thus, if there are large local or temporal variations in price, it is important to give chief weight to the largest purchases.

What has been said as to Q and p arrays relates only to one commodity. But the same principles apply to each commodity yielding separate arrays corresponding to each of the total quantities, Q, Q', Q'', etc., as well as corresponding to each of the average prices, p, p', p'', etc.

§ 4 (TO CHAPTER II, § 5)
"Arrays" of e's, m's, and V's

In the preceding section we have seen that there exists an "array" of p's, pQ's and Q's for each commodity. These relate to the right side of the equation of exchange. Similar arrays relate to the left side.

If, as before, we assume a community of any number of persons, distinguished respectively by subscripts at the right, and if we divide the year into moments, distinguished by subscripts at the left, we may designate the amount of money expended in the first moment by the first person as ₁e₁, the average amount of money he has on hand at that moment as ₁m₁ and his velocity of circulation at that moment (reckoned at its rate per year) as ₁V₁. The expenditure in the moment being ₁e₁, that moment's rate per annum is ₁n_{1 1}e₁, there being n moments in the year, so that the velocity of circulation or rate of turnover per annum, ₁V₁, is

A similar notation may be used to express the amounts expended and held and the velocity of circulation for each member of the community during each moment of the year as shown in the following three "arrays" (inside the lines).

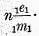
In the first table, E₁ at the right of the first line is the sum expended by the first person, being the sum of ₁e₁, ₂e₁, ₃e₁,...in the first line representing the amounts expended by him at successive moments during the year. Likewise, E₂ is the sum expended by the second person during the year, and E₃ is the sum expended by the third. ₁E at the foot of the first column is the amount expended by all persons in the first moment; that is, it is the sum of all the amounts in the column above it; ₂E is likewise the amount expended by all persons in the second moment; ₃E, the amount expended in the third, etc. Finally, E, in the lower right-hand corner, is, as employed in the text, the grand total expended by all persons in all moments of the year. Evidently E can be obtained by adding the row to the left of it, or by adding the column above it. It is also the sum of all the elements inside the lines, i.e. E = S₁E = SE₁ = S₁e₁.

In the second table, M in the lower right corner is a sum of the average amounts held by the different members of the community during the year, i.e. it is the sum of the elements in the column above it, m₁, m₂, m₃, etc., each of which is by hypothesis a simple average of the row to its left.

Or, again, M is a simple average of the row to its left, ₁M, ₂M, ₃M, etc., the average amounts of money in the community, in the successive moments of the year, each of which averages is in turn the sum of the column above it, i.e.

Thus M is both the sum of averages and the average of sums. That the two are equal follows by expressing both in terms of the elementary quantities ₁m₁ by means of the equations

and the equations ₁M = ₁m₁ + ₁m₂ + ₁m₃ +....It is, of course, easy also to express M directly in terms of ₁m₁, etc., within the table. Thus expressed, it is

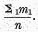
The third table (that for velocities) is derived from the other two. As just explained, ₁V₁ is the velocity of circulation (considered as a per annum rate) for the first person in the community in the first moment.

There remain to be shown the relations of the elements in the V table.

Form (1) shows that V is a weighted average of the yearly velocities of the different persons, the velocity of each person being for the entire year and weighted according to his average amount of money on hand.

Following an analogous but slightly different sequence, we have

Form (2) shows that V is also the weighted average of the yearly velocities of the successive moments into which the year is divided, the velocity of each moment being for the entire community and weighted according to its average amount of money then in circulation.

Thus form (1) gives V in terms of the column above it, while form (2) gives V in terms of the row at its left. A formula similar to (1) may be constructed to express each of the magnitudes ₁V, ₂V, ₃V, etc., in terms of the column above it, while a formula similar to (2) may be constructed to express each of the magnitudes V₁, V₂, V₃, etc., in terms of the row at its left. That is, the velocity in the entire community at any particular moment is a specific form of average of the velocities of different persons at that moment; and the velocity for the entire year of any particular person is a specific form of average of the velocities at different moments for that person.

Finally, V may be expressed, not only as an average of its column and row as in formula (1) and (2), but also as an average of the magnitudes in the interior of the table. This last result may be obtained in several ways, of which the most direct may briefly be expressed as follows: We know that E is the sum of the interior of the first or E table, that is, E = S₁e₁; and that M is equal to

Hence, we have

That is, V is the weighted arithmetical average of the yearly velocities pertaining to different persons in different moments, each velocity being weighted by the amount of money on hand in that instance. The mathematical reader will perceive that an alternative treatment would derive the result in terms of an harmonic average.

§ 5 (TO CHAPTER II, § 5)
The Coin-transfer Concept of Velocity and the Concept of Time of Turnover

We now turn to the coin-transfer concept of velocity of circulation. To show what kind of an average V is of the velocity of circulation of individual coins, or rather of individual pieces of money in general, let us denote the values of the individual pieces of money circulating in the community by the letters a, b, c, d, etc., and let us denote the net velocity of circulation of these (the number of times exchanged against goods minus the number of times exchanged with goods or "in change") by h, i, j, k, respectively, etc. Then E, the total amount expended, is denoted by ha + ib + jc + kd +...; and the amount of money, M, in the community is a + b + c + d.

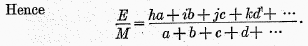
That is, E/M is a weighted average of the net velocities of circulation of the different pieces of money, the velocity of each piece being weighted according to its denomination. But E/M is also V, which we have already seen is the velocity of circulation in the person-turnover sense.

It is clear, therefore, that the coin-transfer method of averaging is the same in results as the person-turnover method, if all the pieces of money in the community are included.

Finally, we come to the concept of "time of turnover."

If velocity of circulation is represented as V, then 1/V represents the time of turnover. Similarly, the reciprocals of ₁V, ₂V,..., V₁, V₂,..., ₁V₁, ₁V₂,..., ₂V₁,..., are corresponding times of turnover. Using W for the reciprocal of V and applying the appropriate subscripts, we may write an array of W's analogous to the previous array of V's, and we may show that W is an average of W₁, W₂, or of ₁W, ₂W,... or of ₁W₁, ₁W₂,...,₂W₁,...

But these averages are all harmonic averages. To see this, we need only remember that V has already been analyzed*3 as a weighted average of the elementary V's, and that W has been defined as the reciprocal of V. That is, W is the reciprocal of this weighted average of elementary V's. But the elementary W's are reciprocals of the elementary V's. In other words, W is the reciprocal of the weighted arithmetical average of the reciprocals of elementary W's. This makes W, by definition, a weighted harmonic average of these elementary magnitudes.

§ 6 (TO CHAPTER II, § 5)
Algebraic Demonstration of Equation of Exchange

It is clear that the equation of exchange, MV = SpQ, is derived from elementary equations expressing the equivalence of purchase money and goods bought. The money expended by any particular person at any particular moment is, by the very concept of price, equal to the quantities of all commodities bought in that moment by that person multiplied by the prices, i.e.

From this equation and others like it, for every person in the community and for every moment in the year, simply by adding them together, we obtain, for the left side of the equation, the sum of the e's which we call E; and for the right side the sum of all the pq's. We have already seen in the text how the left side, E, may be converted (by multiplying and dividing by M) into MV, and we have also just seen (§ 3 of this Appendix) how the sum of all the terms relating to each particular commodity represented on the right side may be converted (by similar simple algebraic operations) into one term of the form pQ so that the whole sum becomes SpQ. The final result is, therefore, MV = SpQ. This reasoning constitutes, therefore, a demonstration of the truth of this formula, based on the simple elementary truth that in every exchange the money expended equals the quantity bought multiplied by the price of sale.

§ 7 (TO CHAPTER II, § 5)
P must be a Specific Form of Average in order to vary directly as M and V and inversely as the Q's

Let us assume that V and the Q's remain invariable while M changes to M_o and p, p', p', etc. to p_o, p'_o, p'_o, etc. (The subscripts "0" refer to a year called the base year other than the original year.) We have for the two years respectively the two equations:—

whence by division, we obtain

The last expression is evidently a weighted arithmetical average of

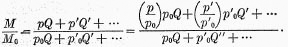
etc., the weights being p_oQ, p'_oQ', etc. We conclude that, if the velocity of circulation and the quantities of goods exchanged remain unaltered, while the quantity of money is altered in a given ratio, then prices will change in this same ratio "on the average," the average being exactly defined as a weighted arithmetical average, in which the weights are the values of goods sold, reckoned at the prices of the base year. The ratio may evidently also be written:—

which is a weighted harmonic average of

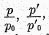
etc., in which the weights are pQ, p'Q', etc., that is, the values, not in the base year, but the other year.

If M and the Q's remain invariable, while V changes from V to V₁, evidently the ratio V/V₁ will be expressed by precisely the same formulæ as above.

If the Q's remain invariable, while M and V both change, evidently the ratio

will be expressed by the same formulæ.

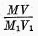
Again the same formulæ apply if M and V remain invariable while the Q's all vary in a given ratio, or if the Q's all vary in a given ratio in combination with any variation in M or V or both. In short, the formulae apply perfectly in all cases of variation, except when the Q's vary relatively to each other.

These formulæ, it should be noted, are those later discussed as the formulae numbered (11) in the large table of formulæ in the Appendix to Chapter X.