The Purchasing Power of Money
By Irving Fisher
THE purpose of this book is to set forth the principles determining the purchasing power of money and to apply those principles to the study of historical changes in that purchasing power, including in particular the recent change in “the cost of living,” which has aroused world-wide discussion.If the principles here advocated are correct, the purchasing power of money–or its reciprocal, the level of prices–depends exclusively on five definite factors: (1) the volume of money in circulation; (2) its velocity of circulation; (3) the volume of bank deposits subject to check; (4) its velocity; and (5) the volume of trade. Each of these five magnitudes is extremely definite, and their relation to the purchasing power of money is definitely expressed by an “equation of exchange.” In my opinion, the branch of economics which treats of these five regulators of purchasing power ought to be recognized and ultimately will be recognized as an exact science, capable of precise formulation, demonstration, and statistical verification…. [From the Preface to the First Edition]
First Pub. Date
1911
Publisher
New York: The Macmillan Co.
Pub. Date
1922
Comments
Assisted by Harry G. Brown (Instructor in Political Economy in Yale U.) 2nd edition. Harry G. Brown, assistant.
Copyright
The text of this edition is in the public domain.
- Preface to the First Edition
- Preface to the Second Edition
- Suggestions to Readers
- Addendum
- Chapter 1
- Chapter 2
- Chapter 3
- Chapter 4
- Chapter 5
- Chapter 6
- Chapter 7
- Chapter 8
- Chapter 9
- Chapter 10
- Chapter 11
- Chapter 12
- Chapter 13
- Appendix to Chapter II
- Appendix to Chapter III
- Appendix to Chapter V
- Appendix to Chapter VI
- Appendix to Chapter VII
- Appendix to Chapter VIII
- Appendix to Chapter X
- Appendix to Chapter XII
§ 1.
Each Form of Index Number for Prices implies a Correlative Form of Index Number for Quantities
APPENDIX TO CHAPTER X
We have seen that the number of possible forms of averages is infinite. Since an index number, as
P1, is an average, it follows that there exists an infinite number of possible forms of index numbers. Forty-four of the simplest and most important forms are given in the table which follows. In this table the subscript “1” relates to any specified year called for convenience “year 1,” while the subscript “0” likewise relates to “year 0,” called the “base” year. The headings of the columns in the table give the formula for the index number,
P1, for the year 1 relatively to the base year 0. By substituting “2” for “1,” each formula could be made to refer to a second year, 2, considered relatively to the base year 0. Likewise, substituting “3,” “4,” etc., for “1,” we have an entire series of index numbers,
P1,
P2,
P3,
P4, etc., for different years, all relative to the same base year 0. Since the formulæ are all alike and differ only in subscripts, it is unnecessary to waste space by expressing
P2,
P3, etc., in the headings. Consequently, in each column heading, only the formula for
P1 is expressed.
Also to save space, the column headings omit the formulæ for
T1, etc., correlative to those for
P1. Each form of price index,
P1, applicable to the equation of exchange, implies a correlative trade index,
T1, such that the product of the two is equal to
Sp1Q1, the right side of the equation of exchange.
Since
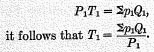
Hence, given a particular formula for
P1, we have a resultant and particular formula for
T1. For instance, if
P1 is a
simple arithmetic average of
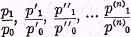 ,
,i.e. if
 ,
,(formula 3 of the table), where
n is the number of commodities of which the price ratios are included, then the correlative formula for
T1 will evidently be
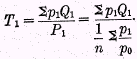
Again, if
P1 is the geometric average
 ,
,(formula 7 of the table), then
T1 has the correlative form
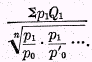
Conversely any particular formula for
T1 implies a correlative particular formula for
P1. For, since
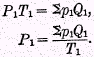
By means of this equation, if we have given any particular formula for
T1, we may obtain a resultant particular formula for
P1.
The examples already given of
P1 (the arithmetical and geometric average) illustrate how to obtain the correlative formula for
T1. If we work backward from these somewhat complicated formulæ for
T1, we may in turn derive as the correlative formulæ for
P1 the arithmetic and geometric averages.
As a third example illustrating the derivation of the formula for
P1 from a given formula for
T1, let
T1 be defined as
Sp0Q1; then
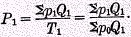
We may consider, then, that each column heading, though stating only the formula for
P1, implies also a corresponding formula for
T1; that is,
P1 and
T1 occur in correlative pairs.
P1 and
T1 are such that if one of them (say
P1) is given independently of the equation,
Sp1Q1 =
P1T1, the other is then defined by means of that equation.
The two magnitudes
P1 and
T1 are not, however, absolutely symmetrical. There is this important distinction between them: that, while
P1 is an
abstract number,
T1 is
concrete, being expressible in dollars and cents.
It thus appears that, although the
p‘s and
Q‘s enter symmetrically into the expression
Sp1Q1, yet, when this expression is replaced by
P1T1, the first factor,
P1, represents the
p‘s in a somewhat different manner from that in which the second factor,
T1, represents the
Q‘s.
P1 is a pure number, an average of pure numbers—the ratios the
p‘s bear to the base prices,
p0‘s, whereas
T1, being
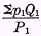
is a concrete number, being a value found by dividing the value
Sp1Q1 by the pure number
P1.
Thus, while the
p‘s and
Q‘s occur symmetrically in the original formula
Sp1Q1, the process by which we convert
Sp1Q1 into
P1T1 treats them asymmetrically. But evidently we can reverse the asymmetry in their treatment; for, instead of putting
Sp1Q1 equal to
P1T1, we may put it equal to
A1Q1, in which
Q1 is now a
quantity index, that is, an average of the ratios which the
Q1‘s bear to the
Q0‘s or base quantities (
i.e. an average of
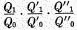 …),
…),and
A1, being therefore
 ,
,is the “aggregate price,” that is, the
value found by dividing the value
Sp1Q1 by the pure number
Q1. Here, if the form of
Q1 is given independently of the equation
Sp1Q1 =
A1Q1, the form of
A1 is defined by means of this equation, and conversely.
Thus we may convert
Sp1Q1 into either
P1T1 or
A1Q1. In the first, the
p‘s are represented by a ratio,
P1; in the second,
by a value,
A1; in the first, the
Q‘s are represented by a value,
T1; in the second, by a ratio,
Q1. The asymmetry of each of the two formulæ
P1T1 and
A1Q1 is the reverse of the other.
Finally we may, if we wish, treat both the
p‘s and
Q‘s
alike by putting
Sp1Q1 equal to (
Sp0Q0)
P1Q1, where
P1 and
Q1 are, both of them, index numbers for the
p1‘s and
Q1‘s respectively. That is (as we shall prove),
P1 and
Q1 are
averages respectively of price ratios like
p1/
p0, and of quantity ratios like
Q1/
Q0. The equation
Sp1Q1 = (
Sp0Q0)
P1Q1 may be said to define either one of the two averages (
P1 and
Q1) in terms of the other. One or the other must be defined irrespective of the equation.
Thus there are three ways of resolving
Sp1Q1, as follows:—
P1T1 =
A1Q1 = (
Sp0Q0)
P1Q1.
The third form becomes, dividing the equation through by
Sp0Q0,

We wish now to prove that if either
P1 or
Q1 is first determined in any way conformably to the definition of an average, leaving the other to be determined by the above equation, then the latter also necessarily conforms to the definition of an average. We have to prove that if
Q1 is taken as an average of
 …,
…,then the correlative expression for
P1 derived from (1), viz.:—

is an average of
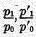 ….
….It is, therefore, only necessary to show (in accordance with the most general definition of an
average as given in the Appendix to Chapter II) that expression (2) shall be equal to
k when

by the definition of an average.
Hence the expression (2) may now be written
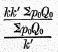
which is evidently equal to
k.
Therefore expression (2) is, by definition, an average of
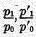 ….
….By the same reasoning we may show conversely
that

is a true average of
 ….
….We conclude that if either
P1 or
Q1 in the formula

is an average of the
p or
Q ratios respectively, then the other is also an average respectively of the
Q or
p ratios.
§ 2.
Index Numbers for Prices occur in Antithetical Pairs as also do Index Numbers for Quantities
We have seen that, given any special form of average for
P1, there results therefrom a correlative form for
Q1 and
vice versa. Thus if
P1 is the simple arithmetical average
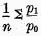
then
Q1 is
 .
.Again, if we start with
Q1 as the simple arithmetical average
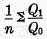
then we discover in its correlate a new formula for
P1, viz.
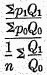 .
.In this way any given formula for
P1 leads to another formula for
P1 which may be called its antithesis. This second formula for
P1 is identical in form with the formula for
Q1 correlative to the first formula for
P1, differing merely in the fact that the
p1‘s and
Q1‘s are interchanged.
The four forms and their relations are best seen by placing them in a square, as in the following example:—

The pair of formulæ in the left vertical column express correlative formulæ, one for
P1 and the other for
Q1. The formula diagonally opposite each of these has the
p‘s and
Q‘s interchanged. The right pair thus formed are evidently also
correlates of each other and each is the
antithesis of that in the same horizontal line at its left. Since any formula for
P1 involves an antithetical formula for
P1, we have here a means of devising new formulæ from old and also of noting certain unsuspected relationships between formulæ already in use.
In the table of index numbers for
P1 which follows, the antithetical formulæ are in each case placed side by side and joined by a bracket. The two together represent, in each case, the upper half of a square like the above. The omitted lower half, giving the correlative forms for
Q1, can be readily supplied in every case; but, to save space, each column heading in the table only includes the formula for
P1, omitting its correlate for
Q1 as well as the corresponding formulæ for
T1 and
A1. The formula for
Q1 is, as above explained, easily written by interchanging
p‘s and
Q‘s in the formula given in the neighboring (antithetical) columns; that for
T1 is found by dividing
Sp1Q1 by
P1; that for
A1 by dividing
Sp1Q1 by
Q1. Practically
P1 and
A1 serve the same purpose, namely, that of indicating price changes; likewise
Q1 and
T1 serve the same purpose, namely, that of indicating quantity changes. For any series of years the numbers for
P1 and for
A1 will be proportional, the only difference being that
P1 is expressed in percentages, the figure for the base year being 100 per cent, whereas
A1 is expressed in dollars, the figure for the base year being the actual exchanges
Sp0Q0 in that year. Likewise
Q1 and
T1 differ merely as percentage and dollar measurements, the base figure being 100 per cent and
Sp0Q0 dollars respectively.
§ 3.
General Meanings of p’s and Q’s
We may here pause to point out that the whole present discussion relates purely to the
form of an index number of
p‘s and
Q‘s without reference to the meaning to be assigned to these
p‘s and
Q‘s. These meanings may be far wider than simply the prices and quantities in the equation of exchange. For example, an index number of prices may be constructed with reference to the purchasing power of a workman’s wages. In this case, the same formula as before,
Sp1Q1, may be employed, but the terms have different meanings. The
p‘s now relate to the prices of goods entering into the workmen’s budgets, and the
Q‘s to the quantities of workmen’s goods entering into their consumption. In this case, the price index,
P, indicates the price level of workmen’s consumption, and the index,
T, means an index for workmen’s
real-wages. Any special form of price index now implies a correlative special form of real-wages index.
Again, if we are studying statistics of capital such as in Giffen’s
Growth of Capital, we have
SpQ as the value of capital, the
p‘s being the prices of different forms of capital and the
Q‘s, their quantities. For every special form of price index number,
P, representing the price level of capital, there will be a correlative special index of
capital showing the real “growth of capital” as distinct from its mere money value. Such an index seems seldom to have been employed.
*11 Yet it is evidently advisable to distinguish between an apparent increase of capital due to inflated prices and a real increase, as would be shown by such an index as here suggested.
We see, therefore, that wherever prices and quantities are united, we have the requisite conditions for constructing correlative pairs of index numbers, one index in each pair relating to prices, and the other to quantities.
We shall, however, for convenience, continue to employ the magnitude
T, rather than
Q, and to refer to it as a “trade” index.
§ 4.
Review of 44 Formulæ, heading the Table Columns
We shall now briefly review the formulæ of the table of selected index numbers. Each even-numbered formula is best regarded as derivable from the odd-numbered formula at its left as its antithesis. The odd formulæ are those constructed directly for the
p‘s without reference to any average for the
Q‘s; the even are constructed indirectly by reference to some average first assumed for the
Q‘s. The latter are what Walsh had in mind under the name of “double weighting.”
Formula (1) is simply the ratio of the sums of prices. It may also be considered as the ratio of the averages of prices in the two years considered, as is evident by writing it,—
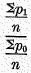 ,
,where
n is the number of commodities employed.
This formula was used by Dutot in 1738,
*12 and has been used recently by Bradstreet,
*13 who applied it practically.
Although it is a ratio of average
prices, it may also be thrown into the form of a weighted arithmetical average of the
price ratios,
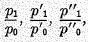 ,
,etc., as the following transformation shows:—
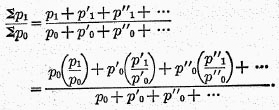
The formula in this last form is evidently the weighted arithmetical average of the ratios in parenthesis, the weights being the prices
p0,
p‘
0,
p”
0,…of the year 0. A change in the units of quantity for the various goods would change these prices; thus a change from ounces to pounds would multiply the number expressing price by sixteen. Such a change in any price, such as
p0, would entirely change the relative importance of the “weights,”
p0,
p‘
0, etc. Consequently this system of weighting is, as Walsh says, quite accidental or haphazard.
*14
The same formula is also a harmonic average, as the following transformations show:—

The last expression is evidently the reciprocal of a weighted arithmetical average of the price ratios in parenthesis. But these price ratios are the reciprocals of
 ,
,etc. In other words, the formula is the reciprocal of a weighted
arithmetical average of the reciprocals of the ratios
p1/
p0, etc. It is therefore the weighted
harmonic average of these ratios
p1/
p0, etc., the weights being
p1,
p1‘, etc., or the prices of the year 1.
In short, formula (1) is both an arithmetical and a harmonic average of
 ,
,etc., the weights being, in the first case, the terms of the denominator, and in the second, those of the numerator.
We have seen that formula (1) in the table, although primarily a
ratio of averages of prices, may be also considered as an
average of ratios of prices with arbitrary weighting.
Conversely we may, if we choose, regard every average of ratios as a ratio of averages by assuming arbitrary units for measuring commodities. It is evident that, if the unit of measure is increased in any ratio, the number expressing the price is decreased in the inverse ratio. If, therefore, we change the unit of measure of a commodity the price of which is at first expressed by
p1 by dividing by the ratio
p0, this price becomes
p1/
p0. Thus
p1/
p0 may be considered to be a price as well as a price ratio. Hence an average of
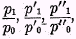
etc., may be regarded as an average of
prices. The new units, instead of being pounds, yards, etc., are
dollars-worth-in-the-base-year. With these units, the price in the base year is unity, for dividing the price,
p0, in the original units by the factor
p0, we obtain unity.
Hereafter, however, we shall treat all index numbers as averages of price ratios.
It is interesting to note that the antithesis of Dutot’s or Bradstreet’s formula (No. 2), found by dividing the fraction

by the correlative formula for
Q1, viz.,
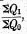 ,
,turns
out to be that advocated by Drobisch,
*15 and earlier by Sir Rawson-Rawson.
*16
Formula (3)
*17 is evidently the familiar simple arithmetical average,—
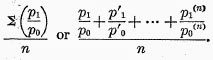
Formula (4), the antithesis of formula (3), gives, as the average price ratio, the ratio of total values
Sp1Q1/
Sp0Q0 corrected for change in the
Q‘s by division by the arithmetical average ratio of the
Q‘s.
Hereafter the even-numbered formulæ, being antitheses of the preceding odd formulæ, will be passed over unless there is, in any case, special reason for mention.
Formulæ (5), (7)
*18, and (9)
*19 are respectively the simple harmonic, simple geometric, and simple median averages. We note that the antithesis of (7), viz. (8), is one proposed by Nicholson and Walsh.
*20
Formula (11)
*21 resembles Bradstreet’s, except that the introduction of the
Q‘s as multipliers prevents the weighting from being arbitrary; for the weights
p0Q1, etc., unlike the weights
p0, etc., are uninfluenced by a change in the units of measurement for commodities. Whether an article be measured in pounds or ounces will not affect the value of a given amount of it. The following transformations show that the formula is a weighted arithmetic mean:—
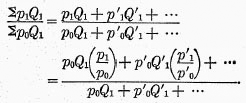
The last expression is evidently a weighted arithmetic average of the price ratios in the parentheses, the weights being
p0Q1,
p‘
0Q‘
1, etc.,
i.e. the
values of the quantities in the year 1 reckoned at the prices of year 0.
But the same formula is also a harmonic average, as may be seen by transforming the denominator instead of the numerator as was done for formula (1). It is a weighted harmonic average, the weights being
p1Q1,
p‘
1Q‘
1, etc., or the values in the year 1.
In short, formula (11) or
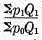
is, like formula (1), both a weighted arithmetical and a weighted harmonic average of
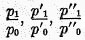 ,
,etc., but the weights are different in the two cases.
(11) has the interesting property that its antithesis (12) is of the same form except that the subscripts for
Q are now 0 in place of 1. Similar reasoning shows that this formula (12) is also both an arithmetical and an harmonic average, weighted according to the terms in its denominator and numerator respectively.
These two formulæ, (11) and (12), seem to be the favorites among writers on Index Numbers. Since the shortcomings of one are, in some cases, not shortcomings of the other, there have been many attempts to combine them into some composite. No. (13),
*22 for instance, is their simple arithmetical average. The antithesis of (13), viz. (14), turns out to be the simple harmonic average of (11) and (12). Number (15) is the simple geometric average of (11) and (12). This formula (15) has the distinction of being identical with its own antithesis (16). Numbers (17), (19), (21), and (23) are other attempts at combining (11) and (12), not by averaging them, as was the case with (13) and (15), but by averaging their coefficients, viz.,
Q1 and
Q0,
Q‘
1, and
Q‘
0, etc. Two antitheses of these, namely (18) and (22), turn out to be formulæ proposed by Walsh, and a third (24) to be one proposed by Julius Lehr.
*23
We have seen that the formulæ (11) and (12) considered as arithmetical averages have for weights

thus completing the four permutations of the subscripts, 01, 00, 11, 10. Number (29) represents a weighted arithmetical average in which the weights are derived from other considerations than the product of the prices and quantities of the base year (1). An instance is the method employed in some of the tables in the “Aldrich Report,”
*24 the weights being the percentage of consumption of various kinds in workingmen’s budgets without reference to the base year or any other particular year.
Numbers (31) and (33) are weighted harmonic means in which the weights instead of being

thus completing for harmonic averages the same permutations of subscripts as before for arithmetical averages. We see then that the odd formulæ (11) to (33) inclusive are merely arithmetical averages or harmonic averages of
p1/
p0 etc., or else averages or mixtures of such averages.
Numbers (35), (37), (39), (41) are various forms of weighted geometric averages of those price ratios, the weights being
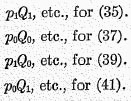
Number (43) is the ratio of the weighted geometric average of the prices in years 1 and 0, the weights being
p1Q1, etc., for year 1 and
p0Q0, etc., for year 0.
It will be seen that all of the 44 formulæ selected for the table are based on a few simple principles of averaging. Most are arithmetic, harmonic, or geometric averages or their combinations. Needless to say, numerous other and more complicated forms might be constructed.
§ 5.
Review of Eight Tests, heading the Table Rows
Having reviewed the headings of the vertical columns of the table, we have next to note the headings of the horizontal rows. These headings are the eight tests of index numbers. The first six tests are arranged in pairs, the odd being expressed in terms of prices and the even in terms of quantities.
THE EIGHT TESTS FOR A GOOD INDEX NUMBER
The eight tests are intended to include all the tests which have been hitherto applied in the study of index numbers and some others. They are:
1. Test of proportionality, as to prices.
2. Test of proportionality, as to trade.
3. Test of determinateness, as to prices.
4. Test of determinateness, as to trade.
5. Test of withdrawal or entry, as to prices.
6. Test of withdrawal or entry, as to trade.
7. Test by shifting base, both as to prices and as to trade.
8. Test by shifting unit of measurement, both as to prices and as to trade.
We shall first define each of these tests in general terms and then proceed to illustrate them by actual applications.
1.
Test of proportionality as to prices. A formula for the price index should be such that the price index will agree with all individual price ratios when these all agree with each other. Thus, if in 1910 the price of everything is 10 per cent higher than in 1909, the index number should register 10 per cent higher.
2.
Test of proportionality as to trade. Likewise the correlative formula for the trade index should be such that the trade index will agree with all individual trade ratios when these all agree with each other.
3.
Test of determinateness as to prices. A price index should not be rendered zero, infinity, or indeterminate by an individual price becoming zero. Thus, if any commodity should in 1910 be a glut on the market, becoming a “free good,” that fact ought not to render the index number for 1910 zero.
4.
Test of determinateness as to trade. The correlative trade index should not be rendered zero, infinity, or indeterminate by an individual quantity becoming zero. Thus, if any commodity should go completely out of use in 1910 so that its quantity exchanged becomes zero, that fact ought not to render the trade index for 1910 indeterminate.
5.
Test of withdrawal or entry as to prices. A price index should be unaffected by the withdrawal or entry of a price ratio agreeing with the index. Thus, if the price index of a certain number of goods, not including sugar, should be 105 in 1910 as compared with 1900, and the price of sugar itself should be 105 in 1910 as compared with 1900, then the inclusion of sugar in the calculation of the index number ought not to change the index from 105.
6.
Test of withdrawal or entry as to trade. The correlative trade index should be unaffected by the withdrawal or entry of a quantity ratio agreeing with the index.
7.
Test by changing base. The ratios between various price indexes (and therefore also, as we shall see, the ratios between the correlative trade indexes) should be unaffected by reversing or changing the base. Thus, if the index number for 1910 is twice that for 1900, when calculated on the basis of 1860, it should remain twice, when calculated on the basis of 1870.
8.
Test by changing unit of measurement. The ratios between various price indexes (and therefore also, as we shall see, the ratios between the correlative trade indexes) should be unaffected by changing any unit of measurement. Thus, if the index number for 1910 is twice that for 1900 when coal
is measured by the ton, it should remain twice, when coal is measured by the pound.
The statements of tests 7 and 8 are expressed in each case both as to prices and quantities; in these cases it was implied that what holds true of price indexes holds true also of trade indexes, and
vice versa. To show this reciprocal relation for test 7 (base shifting), let the price index for year 1 in terms of year 0 be designated by
P1, 0 instead of by
P1 as heretofore, in order that the base year may be specifically designated, and let us compare years 1 and 2 by using first year 0 as a base and then (say) year 8. If the base-shifting test is fulfilled for the
P‘s,
i.e. if
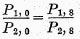 ,
,we are to prove that the corresponding relation is also true for the
T‘s, viz.
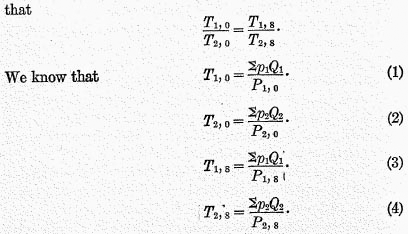
Divide (1) by (2) and (3) by (4). The quotients are
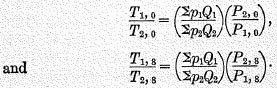
Comparing the right sides of these equations, we find that the ”
S” ratios are identical in the two cases, and we know that the
P ratios are equal by hypothesis. Consequently
the entire right sides of the two equations, and therefore the left sides, are also equal, and this is what was to be proved. The converse reasoning is also evident.
Like the base-shifting test, the unit-shifting test, No. 8, cannot apply to prices without applying also to quantities, and
vice versa. To show this we employ the equation
 .
.Evidently the numerator of the right side of this equation is unaffected by a change of unit. For instance, if coal should be measured in ounces instead of tons, thus greatly increasing the number (say
Q) representing its quantity, the value (
pQ) will not be disturbed, since the number (
p) representing the price will be correspondingly diminished. Consequently, if the denominator (
P) meets the corresponding test,
i.e. is likewise unaffected by a change in unit, the quotient (
T) must be unaffected. That is, if the unit-shifting test is met for
P, it must be met for
T. As the converse reasoning also applies, the proposition is proved.
As will have been noted, the first six tests are expressed alternately in terms of
prices and in terms of quantities. We now wish to point out that those expressed in terms of prices have a significance for quantities also, and that those expressed in terms of quantities have a significance for prices as well. That is, all the tests have significance both as to prices and as to quantities.
To emphasize this fact, which is important, let us note the
price significance of each test. Since the price significance of tests 1, 3, 5, 7, 8 is evidently expressed in the statement of the test, we have left merely to express the price significance of tests 2, 4, 6.
Test 2 tells us that if all the trade ratios agree, their index should agree with them; that is,
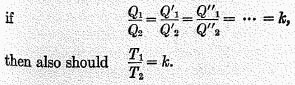
The question now before us is, assuming this condition to hold as to the
Q‘s, what condition holds true as to the
p‘s. The answer evidently is:—
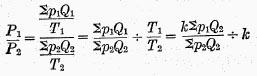
[obtained by substituting
kQ2 for
Q1,
kQ‘
2 for
Q1, etc., and
kT2 for
T1]
 .
.The last form is derived from the next to the last by multiplying both numerator and denominator by
k and then substituting
Q1 for
kQ2,
Q‘
1 for
kQ‘
2, etc.
The resulting two formulæ for
P1/
P2 express test No. 2 in terms of the conditions to which
prices must conform. These formulæ will be recognized as those discussed in § 7 of the Appendix to Chapter II, the significance of which was there explained. It was there shown that a change in
M, or a change in
V, or a
uniform change in all the
Q‘s, or any combination of these changes will, through the equation of exchange, affect the price level in the manner expressed by the formula:—

Thus the equation of exchange itself prescribes test No. 2; for the fundamental theorems which the equation of exchange has taught us are that prices vary directly as
M and as the
V‘s and inversely as the
Q‘s; and the only forms of index numbers which will faithfully reflect these changes,
i.e. will vary directly with
M and inversely with the
Q‘s (assuming that all
Q‘s vary in unison), are those forms of index numbers which conform to test No. 2. Any other form of index number, when
M (and
M‘) increased 50 per cent and there was no change in
V‘s or
Q‘s, might register a rise of 49 per cent
or 51 per cent. That is, no other forms of index numbers will enable us to say that when the quantity of money changes, the velocity of circulation and the
Q‘s remaining the same, the index number of prices will vary proportionately. No other forms will enable us to state the corresponding theorem as to the effect of a change in velocity or of a (uniform) change in the
Q‘s. But these theorems are fundamental. The very concept of an index number is that it shall replace the divergent individual variations and enable us to state of its proportionate changes the same theorems which hold true when prices all change alike.
Test No. 2 is therefore of such fundamental importance that we may profitably pause a moment to restate it in words. To be concrete, let us suppose two years, 1900 and 1910. Let us assume that the quantity of every kind of goods sold in 1910 is (say) exactly double the quantity sold in 1900. Then the only proper index number showing the level of prices in 1910 (year 1) as compared with the level of prices in 1900 (year 0) is
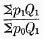
the ratio of the total value of the goods sold in 1910 to what that value would have been at the prices of 1900; or, what amounts to the same thing, it is
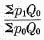
the ratio of what the total value of the goods sold in 1900 would have been at the prices of 1910 to what it actually was at the prices of 1900.
Of the 44 formulæ in the table, only the following reduce to the required formula when the
Q‘s change uniformly: (2) of Drobisch, (4), (6), (8), (10), (11), (28), (30), (34), (38), (40). All these are even-numbered except formula 11. Several others will reduce to the required formula, provided one of the years compared is the base year.
The formulæ of the tables which fail to meet test 2 at all would not even allow us to say of
MV+
M‘
V‘=
PT that if all the
Q‘s remain the same,
T will remain constant and
P will vary as the other side of the equation. For these formulæ
T fails as a true index of the
Q‘s, and its error
in one direction implies a corresponding error in
P in the opposite direction.
Test 2 seems therefore in some respects the most important of all the eight tests for prices; although primarily it was not stated in terms of prices, but in terms of quantities. It is the only test which indicates the kind of
weighting required. It completely prescribes the conditions which, while permitting any individual changes in prices, however divergent, enable us to say that a change in
M or the two
V‘s or in all the
Q‘s in a given ratio will affect prices “on the average” in that same ratio (directly, of course, for the
M‘s and
V‘s and inversely, for the
Q‘s).
Test 2 in fact points out the true form of the index number of prices as prescribed by the equation of exchange under all possible circumstances
except when the
Q‘s vary in unequal proportions. It also points to the proper weights required. These weights may be said to depend either on the
Q1‘s or on the
Q0‘s, interchangeably. The formula suggested by the
Q1‘s is formula 11; that suggested by the
Q0‘s is formula 12. Either will be
perfectly satisfactory when the
Q1‘s and
Q0‘s are proportional, while when they are not, their discrepancy is negligible. When the
Q‘s vary unequally, however, there seems to be
no perfectly satisfactory formula. Under these circumstances the two systems of weights—one in terms of
Q1‘s, the other in terms of
Q0‘s—conflict with each other. But the conflict has been shown by Edgeworth
*25 to be slight. In fact, the weights are of much less importance in determining an index number of prices than the prices themselves.
The discussion of test 2 will be resumed later when in § 7 we come to compare the various forms of index numbers.

As to test 4, this states that if an individual
quantity becomes zero this fact should not render the quantity or trade-index zero, infinity, or indeterminate. But according as the index does or does not become zero, infinity, or indeterminate, will the price index become or not become infinity, zero, or indeterminate respectively. This is clear from the relation
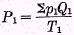 .
.Hence test 4 possesses a significance as to prices similar to that which it possesses as to quantities.
The price significance of test 6 is more complex and of no apparent importance. Its statement is included in the explanatory table on LF-BK133Page 407. In the preceding table of 44 index numbers the “score” for test 6 is bracketed to indicate that it has no important price significance, and is to be omitted in the totals.
Mutatis mutandis, each of the tests expressed in terms of prices (tests 1, 3, 5) has a significance as to quantities also.
The preceding explanatory table exhibits in algebraic terms both hypothesis and conclusion for each of the eight tests with respect both to prices and quantities.
§ 6.
The Interior of the Table; Column 11 in Particular
We have reviewed briefly the headings of the table, including both those of the vertical columns and those of the horizontal rows. Their relations to each other are contained in the interior of the table. The object of the table is to show the degree of conformity of the 44 various formulæ for
P (and their correlates for
T) to the eight tests. In spite of all the mathematical ingenuity spent by many writers in devising index numbers, no known formula and apparently no possible formula will meet all eight of the tests.
For each test we note three possible degrees of conformity. It may be fulfilled by any particular formula in three degrees of conformity or nonconformity: (1) completely, (2) partially, or (3) not at all. These three degrees are indicated in the table which follows, by the numbers 1, ½, 0 respectively.
A test is completely fulfilled by index numbers for
any two years whatever (as year 1 and year 2). A test is
partially fulfilled if it is fulfilled by index numbers for two years,
one of which is the base year (year 0). Thus the former relates to the general case, the latter to a particular case. Since the general includes the special, if the test is fulfilled in general it is fulfilled in particular; the converse is not necessarily true. But if the test is
not fulfilled in the particular case, it is not fulfilled in general; the converse of this proposition is not necessarily true. In short, an affirmative answer to the question of complete conformity carries with it an affirmative answer to the question of partial conformity; and a negative answer to the question of partial conformity carries with it a negative answer to the question of complete conformity. These two rules save much labor in working out the figures in the table.
Our next task is to illustrate the eight tests by applying them to a particular formula for
P1 and the correlative formula for
T1. We select for this illustration the pair of formulæ numbered (11) in the table, namely
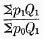
and
T1 =
Sp
0Q1, and we seek to know how far this pair of formulæ conform to the eight tests.
TEST 1.
Proportionality as to prices.—We shall begin with “the particular case” where one of the two years compared is the base year. In concrete terms, this test means that, if all prices for the year 1 are any given number of times (
k times) the prices for the base year 0, then the index number for the year 1 (in terms of the year 0) should be the same number
k.
The test is best expressed in algebraic language as follows:—
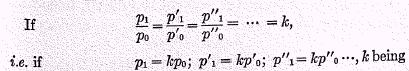
the given constant price ratio, then also should
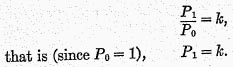
It is easy apply this test to our given pair of formulæ.
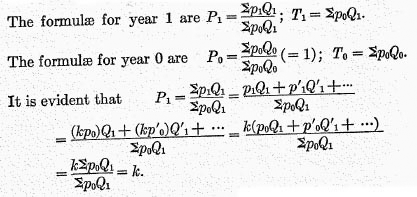
Therefore test 1 is fulfilled for the particular case when one of the years is the base year.
But, as we have noted, it does not follow that the test is fulfilled
in general. For “the general case” of any two years the test may be thus stated: If the price of each good for the year 1 is
k times the price of the same good for the year 2, then the index number for the year 1 (in terms of the year 0) should also be
k times the index number for the year 2 (in terms of the year 0). That this may be true, the test requires, for the general case, that if
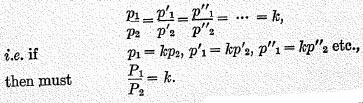
This general test, however, will not be fulfilled, as may be seen from the following:—

In order that this last expression should reduce to
k, it is evident that

would have to be equal to
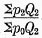 .
.But this cannot be assumed to be always true. If this equality should happen to hold true for any particular value of (say)
Q2, it would evidently be disturbed by the slightest deviation from that value. If, for instance,
Q2 should vary, the left side,
 ,
,of the supposed equality would be unaffected, but the first term in the numerator and the first term in the denominator of the right side would vary. Consequently the right fraction
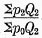
would be affected, except when the ratio of the first term,
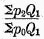 ,
,happened to be equal to
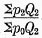 ,
,in which case by a well-known principle of proportion (the principle of “composition and division”) the size of the terms
p2Q2 and
p0Q2 would be immaterial.
The first test, therefore, is fulfilled for the particular case where one of the two years compared is the base year, but is not fulfilled in general. Therefore, following our convention, we assign to formula 11 the number ½ as representing its degree of conformity to test 2.
TEST 2.
Proportionality as to trade. This test, stated for the
general case, is: If the quantities of all goods sold in the year 1 is
k times the quantities of the corresponding goods sold in the year 2, the index number of trade for the year 1 (in terms of the year 0) should also be
k times the index number for the year 2 (n terms of the year 0).

We shall find that this test is fulfilled in the general case, and therefore also in the particular case.

which was to have been proved. Therefore test 2 is completely fulfilled, and the formula is therefore assigned the full credit, “1,” in the table.
TEST 3.
Determinateness as to prices. This test is also completely fulfilled.
If, in the formula for
P1, namely
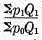 ,
,some but not all of the prices, as
p1, or one of the quantities, as
Q1, should become zero, it is clear that the above expression would still be determinate, and lie between zero and infinity. It will merely happen that some of the numerous terms in the numerator will vanish, but all the other terms will remain.
Since the same reasoning applies to
P2, it follows that
P2/
P1 must also be determinate, being the quotient of two finite, non-zero, and determinate numbers. Thus test 3 is completely fulfilled.
TEST 4.
Determinateness as to trade. The fourth test is analogous to the third, and states that the trade index number must not be rendered indeterminate, zero, or infinity simply because some price or prices should become zero. The formula for
T1 is always
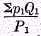 .
.Since, as neither the numerator nor the denominator of this fraction becomes zero, infinity, or indeterminate by the vanishing of some but not all of the
p‘s or
Q‘s, the quotient must likewise be nonzero, finite, and determinate. Thus, test 4 is completely fulfilled.
*26
TEST 5.
Withdrawal or entry as to prices. Suppose that there are 100 specified commodities. If the general price level of one year s
k times that of another, and if any good, the price of which in the one year is
k times that in the other, be withdrawn from the 100 commodities, leaving 99, then the ratio of the price levels of the two years should remain unchanged.
This is a difficult test to meet, and the formula under discussion meets it only partially, that is, when one of the two years compared is the base year.
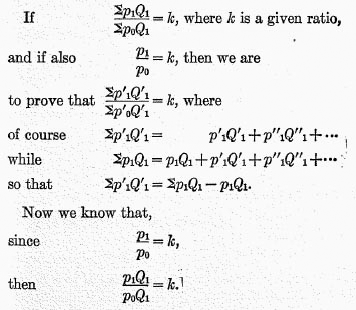
And, since
 ,
,it follows by the principle of proportion
(“composition and division”) that
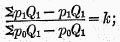
that is,
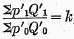 ,
,which was to have been proved.
If the missing commodity is reëntered, the ratio will evidently be undisturbed, so the rule works both ways,
i.e. for entry as well as for withdrawal. Therefore, test five is fulfilled for the particular case.
When, however, we consider the general case for price ratios of two years neither of which is the base year, the test will not be fulfilled.

For, if this expression should happen to be equal to
k in any particular instance, a slight change in any base year price, such as
p‘
0, would disturb the equality, unless the variation in
p‘
0 should affect the denominators of both numerator and denominator of the last expression in the same proportion. This would mean that the ratio
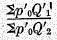
would be unaffected by a change in
p‘
0, which in turn would assume (by the principle of “composition and division”) that
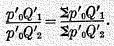
This is not necessarily true, as it is evidently easy to assume values for (say)
Q‘
1 which would render it untrue. Thus, a doubling of
Q‘
1 would double the left side but not the right. Therefore test five is only partially met by our formula. This is therefore to be credited only with ½ as its degree of conformity to test 5.
TEST 6.
Withdrawal or entry as to trade. If the index numbers for trade are in a given ratio, the inclusion or exclusion of a given good, the quantities of which are in the same ratio, ought not to disturb that ratio. This test is completely fulfilled by our formula.

TEST 7.
Changing the base. This test 7 is not fulfilled by our formula even in the particular case. The particular case means here the case of
reversing the base, as between (say) year 1 and year 0.
In order not to alter and thereby confuse the notation we shall have to use the subscript 0, which indicated the original base year, to indicate that same year, even when, for the moment, it is not considered as the base year; and likewise we shall use the subscript 1 to indicate the year 1, even when it is, for the moment, taken as the base year.
By the formula which we are testing, the price index ratio for year 1 compared to year 0 as the base is
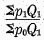 .
.By analogy it is clear that the price index ratio for year 0, compared with year 1 considered as the base, is
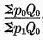 .
.If these two expressions are reciprocals of each other, then

should be equal to
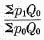 .
.That this is not necessarily true is evident, since there is no necessary relation between the
Q0‘s and the
Q1‘s. If the equation should accidentally hold true for a particular set of
Q0‘s and
Q1‘s, the change, even in the smallest degree, of a single letter, say
Q0 or
Q1, would evidently disturb the relation. Therefore the test is not fulfilled even for the particular case of reversing the base as between two years, and the formula must therefore be assigned a “0” or complete failure to conform to test 7.
TEST 8.
Changing units of measurement. If the unit for indicating the price, say of coal, should be changed from a ton to a pound, the index number ought not to be affected thereby. We shall find that this test is met by formula (11).
Evidently a change of unit, say from a ton to a pound, applied to any particular goods (the prices of which are
p1,
p‘
1,
p”
1, the corresponding quantities being
Q1,
Q‘
1,
Q”
1) will magnify all the
Q‘s 2000 times, but, on the other hand, will reduce all the
p‘s in the reciprocal ratio (1/2000). Consequently, the products
p1Q1,
p‘
1,
Q‘
1,
p”
1Q”
1, will be unaffected.
Hence the sum of such products constituting the numerator and denominator of the right side of the equation

will likewise be unaffected. Therefore the ratio of the index numbers
P1/
P2 will be unaffected. Hence the test is completely fulfilled.
*27
§ 7.
The 44 Formulæ Compared
We have gone through the reasoning by which the conformity of one pair
P1 =
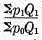 ;
;T1 =
Sp0Q1)
out of the 44 pairs of index numbers of prices and trade, given in the table, are tested and graded with respect to the eight tests. The table contains for the remaining 43 formulæ the results of similar reasoning. This reasoning is here omitted to save space. The mathematical reader who chooses can verify the results as tabulated. He can also prove the relationship by which it follows that the figure in any column for the odd tests corresponds to that in the neighboring antithetical column for the even tests. In consequence of this relationship the sum of any column for the odd tests equals the sum in the antithetical column for the even tests. In fact, the table is full of correspondences and relationships of many kinds.
The footings give us a means of comparing the merits of the various index numbers. These footings are intended to express, so far as may be, the fitness of the formulæ to serve as index numbers for price levels. Consequently the score for test 6 should be omitted from the footing, as test 6 has no value in regard to
prices. (If it be desired to compare the scores of the correlative index numbers for quantities or trade, the score of test 6 will be included, but that of test 5 should then be omitted.)
Thus a perfect score would be
seven. The highest score in the table is 5½, the lowest, 2.
It would, of course, be absurd to compare the merits of index numbers merely by their “score” in the table. This score is more or less arbitrary, and it treats all seven tests as equally important. Yet it affords at least some insight into the comparative characteristics of the 44 formulæ. It is noteworthy that, in general, the simplest formulæ have high scores and the most complicated have low scores. Thus formulæ 1 (Dutot), 7 (simple geometric), 9 (median), 11 and 12 (Scrope) have scores of 5 and 5½. The only others as
high as 5 are “mixtures” of formulæ 11 and 12. The simple arithmetical (3) and simple harmonic (5) have a score of 4, which is fairly high. The more complicated forms which have fairly high scores are in several cases “mixtures,” averages, or antitheses of simple formulæ 11 and 12.
The above comparisons treat all the other seven tests as of equal importance. But they are not of equal importance. Since opinions might differ as to the exact relative importance of the various tests, we shall not attempt to “weight” them. Nor will this be necessary in order to decide the question of most importance to us, viz., which of the 44 index numbers meet the tests most completely. Tests 3 and 4 are probably of little practical importance as compared with the remaining tests. Test 2, on the other hand, may be accorded chief importance, for reasons given in section 5 of this Appendix and in Chapter II. In order to select the best index numbers of prices, therefore, let us first rule out of the competition all the 18 formulæ which have “0” for test 2. We have left the following formulæ classified into two groups.
(Omitting test 6), score for formulæ which do not completely fail on test 2,
| FORMULÆ COMPLETELY FULFILLING TEST 2 |
FORMULÆ PARTIALLY FULFILLING TEST 2 |
||
|---|---|---|---|
| Formulæ | Score | Formulæ | Score |
| 2 | 4 | 12 | 5½ |
| 4 | 3 | 13 | 4 |
| 6 | 3 | 14 | 4 |
| 8 | 4 | 15 | 4½ |
| 10 | 4½ | 16 | 4½ |
| 11 | 5 | 17 | 5 |
| 28 | 4 | 18 | 4½ |
| 30 | 3 | 20 | 4 |
| 34 | 3 | 21 | 5 |
| 38 | 3 | 22 | 4½ |
| 24 | 4 | ||
| 26 | 3½ | ||
| 32 | 2½ | ||
| 36 | 2½ | ||
| 42 | 2½ | ||
If, next, we rule out of the competition from among those which completely meet test 2, all except those which have scores of 4½ or above, we have left only formulæ numbers 10 and 11. Among the formulæ which only
partially meet test 2 we may eliminate all which fail to
exceed 4½ in total score; for, although those which reach 4½ tie formula 10, yet when all tests are counted as of equal importance, they are inferior in not completely meeting the most important test—test 2. Putting the matter in another way, we may say that if test 2 should be weighted more heavily than the other tests, the scores of those formulæ
half meeting that test which now tie formulæ
wholly meeting that test would fail to do so and would therefore drop out of competition with formulæ 10 and 11 in the first column.
Eliminating therefore from the second column all formulæ with scores of 4½ or less, we have as the only rivals of formulæ 10 and 11, formulæ 12, 17, and 21, having scores of 5½, 5, and 5 respectively. Our best formula, therefore, should be found among numbers 10, 11, 12, 17, 21. We shall therefore examine with particular care these five surviving competitors.
These all conform to tests 3, 4, and 8. Comparing them in other respects, we find:—
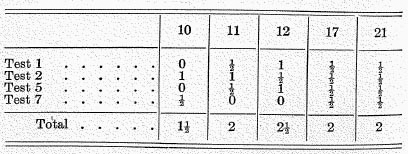
Tests 17 and 21 have scores identical in every instance, and may therefore be said to be
tied.
Comparing tests 11 with 17 (or 21), we see that 11 excels in respect to the important test 2, and 17 in test 7. As test 2 is regarded as of more importance than test 7, we may
safely give the preference to formula 11 over 17 (or 21). We therefore now strike out 17 and 21 from the competition.
We have left formulæ 10, 11, 12; comparing 10 and 11, we note that 10 excels in test 7, while 11 excels in tests 1 and 5. If we may be allowed here to exercise a comparative judgment, we shall say that the superiority in the one test 7 is more than offset by superiority in the two tests, 1 and 5. We therefore eliminate formula 10.
We now have left only the two formulæ, 11 and 12. There is not much to choose between them. While 12 has the higher score when all tests are counted as of equal importance, 11 excels in the most important test 2, and we are therefore inclined to give it the preference.
According to our judgment, therefore, test 11 emerges as the winner in the score contest. It has also the advantage of being among the very simplest formulæ and of having as its correlative formula for
T the simplest of all formulæ for
T, viz.
T1 =
Sp0Q1.
In nonmathematical language, the pair of formulæ 11 mean that
the level of prices in any year is found by dividing the total value of the quantities sold in that year by what that value would have been at base prices, and that the trade index in any year is simply the value of the quantities sold in that year
reckoned at base prices.
Applying formula 11 to the equation of exchange, we have—

We wish now to emphasize once more the virtues of this formula 11 in respect to test 2. The equation of exchange, stated above, is intended to show how prices are affected by changes in
M,M‘,
V,V‘ or the
Q‘s. It is evident from the original form (1) of this equation that a proportional change in the
M and
M‘ (if the
V‘s and
Q‘s remain unchanged) will
affect all the
p1‘s in exactly the same ratio, or else raise some prices more and others enough less than this ratio to compensate in the sense that the equation of exchange will be preserved. In some sense, therefore, the general
level of prices varies exactly with
M and
M‘. Form (3) enables us to express this proportionality by formulating the price level as the fraction
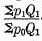 .
.This varies directly with the
M‘s.
In precisely the same way we are enabled to state that a uniform change in the two
V‘s, or any change in the left side of the equation as a whole, will affect prices in precisely the same ratio (the
Q1‘s being assumed constant). We may also say that a
uniform change in the
Q1‘s will affect
T1 in exactly the same ratio, and
P1 in exactly the inverse ratio (assuming the left side of the equation to be unchanged). In fact, if we use formula 11 to express the average price ratio, we are able to state in all cases (so long only as the
Q1‘s change in unison or not at all) that prices rise or fall “on the average” directly as the left side of the equation, and inversely as the
Q1‘s.
As noted, these are the basic theorems for which the equation of exchange stands. We would naturally like to remove the restriction as to the
Q1‘s changing uniformly. We should consider an index number perfect (so far as needed in the equation of exchange) if we could assert of it the same theorem of proportion as above, without the restriction as to the
Q1‘s changing uniformly, so that we might substitute an
average change in the
Q‘s in place of a uniform change. No such index is found in the table, and no such index seems possible. Practically this conclusion does not greatly matter, for we are interested in prices far more than in quantities, the latter being chiefly important as supplying weights for the price indexes. As we have already noted, Edgeworth has shown that considerable variation in weighting is of comparatively little practical importance.
The chief use of index numbers is to compare
successive years, not years remotely distant from each other. We are
not so much interested in comparing the prices of 1909 and 1910 each with those of 1873 as we are in comparing them with each other. In fact, the chief use of 1873 as a base year is to enable us to compare any other two years with each other. But only a few index numbers which afford a true comparison between any year and another year as the base will give a true comparison between any two years, each in terms of a third year as the base. These few index numbers are those which completely meet the base-shifting test 7.
*28 In the table the only formulæ which come up to this requirement are formulæ numbered 1, 2, 7, 8, 43, 44, to all of which there are serious objections on other grounds. Formulæ 1 and 2 are very arbitrary, having “haphazard weighting”; formulæ 43 and 44 have the lowest scores in the table; formula 7 has no system of weighting; and formula 8 becomes zero if a single quantity, as
Q, should disappear from a year’s sales.
The question therefore arises, why should we, as has usually been done, construct out index numbers with reference to a fixed base in terms of which we
indirectly compare two given years? Why not make the comparison
directly? The indirect comparison introduces an error in all cases except of those formulæ which conform to test 7. In these cases the indirect comparison cannot, of course, give any better result than the direct comparison, while in all other cases the direct comparison is better.
It seems, therefore, advisable to compare each year with the next, or, in other words, to make each year the base year for the next. Such a procedure has been recommended by Marshall, Edgeworth, and Flux.
*29 It largely meets the difficulty
of non-uniform changes in the
Q‘s, for any inequalities for successive years are relatively small.
Such
successive index numbers, each on the basis of 100 per cent for the previous year, will, if multiplied together, give a
chain of index numbers showing the fluctuations from year to year, like any ordinary series, but much more suitable for comparison of neighboring years.
Let us now reëxamine the comparative merits of index numbers on the supposition that they are to be used only for successive years, that is, for comparison between each year and the previous year as a base. In this case we do not need to distinguish between a “partial” and a “complete” fulfillment of the tests. We may therefore now substitute “1” for every “½” Omitting, as before, all formulæ which fail to meet test 2, we have the following results:—
| FORMULA | SCORE | FORMULA | SCORE |
|---|---|---|---|
| 2 | 4 | 20 | 5 |
| 4 | 3 | 21 | 7 |
| 6 | 3 | 22 | 6 |
| 8 | 4 | 24 | 5 |
| 10 | 4½ | 26 | 4 |
| 11 | 6 | 28 | 4 |
| 12 | 6 | 30 | 3 |
| 13 | 5 | 32 | 3 |
| 14 | 5 | 34 | 3 |
| 15 | 6 | 36 | 3 |
| 16 | 6 | 38 | 3 |
| 17 | 7 | 40 | 3 |
| 18 | 6 | 42 | 3 |
| 19 | 6 |
We note that formulæ 11 and 12 have scores of 6 each, while their average 15 (and 16) and their mixture 18 and also 22 have the same score, but that formulæ 17 and 21, which are mixtures of 11 and 12, have perfect scores, 7. Each of these two formulæ uses as weights the average of the weights used in formulæ 11 and 12. Theoretically, therefore, we find two formulæ which fit all tests perfectly so far as year-to-year comparisons of prices are concerned.
Where, therefore, great accuracy is desired and there exist abundant funds to provide for the laborious computations necessary, we may recommend the use of formula 17 or 21. This presupposes that statistics are available for the
Q‘s, which is not usually the case.
Thus far our conclusions therefore are (1) that theoretically formula 11 is the best when each year is expressed in terms of a common base; (2) that (also theoretically) formula 17 and 21 are slightly superior when each year is expressed in terms of the preceding year as base, and that these two meet
all tests for year-to-year comparisons.
§ 8.
Reasons for preferring the Median for Practical Purposes
Practically, however, there is little if any advantage in 17 and 21 over 11 (or 12, which in the case of year-to-year comparisons amounts to the same thing) because (1) weighting is of little importance; (2) the more perfect weighting contained in formulæ 17 and 21 will seldom differ materially from that of 11 and 12, for any gain of precision would probably be less than the errors in measurement of the
Q‘s, which are never exactly known; (3) the systems of 17 and 21 are practically far more laborious. In the end we must be guided largely by practical considerations except where the great labor and expense of computation may be disregarded. If in a
practical spirit we examine the merits of the various formulæ, we shall, I believe, reject all formula except 9 and 11, and come to the conclusion that the best index number is the
weighted median. It has no rival in ease of computation. The score of the median in the table (formula 9) is high, although it fails in test 2. Excepting this test it meets, partially or wholly, every other test. It therefore possesses some merit even on the theoretical side.
In passing, we may mention a feature of medians, although I am disposed to regard it as a fault. Edgeworth emphasized the fact that price
dispersion upward always or usually exceeds the price
dispersion downward. There is no limit to
the former, but the latter is limited by zero. Statistical tests show clearly this asymmetry of dispersion.
*30 From this fact it has been argued that the best average should be one from which large deviations above it count no more than small deviations below it. This condition, whether good or ill, is not met by arithmetical averages, but is met by the geometric average and by the median
*31 which, in fact, usually closely follows the geometric average. Edgeworth also argues that the median is superior when the variabilities of the various elements averaged are widely different.
*32
Edgeworth concludes that “in the present state of our knowledge, and for the purposes on hand, the median is the proper formula.”
*33
As to methods of weighting, theoretical discussion with reference to test 2 shows that the weighting should be made on the basis of values sold in one or the other of the years compared.
It is easy to show that a system of weighting the median by given weights, that is, by counting each price ratio, not only
once but a certain number of times (that number being the weight) will not affect the relative fulfillments of the tests as met by the simple median 9, which is the only median in the table. Edgeworth has shown that for all practical purposes a very rough system of weighting will suffice.
*34 Whether the weighting be according to the values
p0Q0, etc., or
p1Q1 etc., or
p0Q1, etc., or
p1Q0 etc., is usually of no practical importance whatever. If, then, we subordinate theoretical to practical considerations, the proper procedure would seem to be to select certain constants consisting of simple integers, and as near as may be to the values dealt with in the years considered. These weights need not be changed every year, but should be changed when the values (
p1Q1) change very greatly.
If it be desired to have a quantity or trade-index number (
Q1, or
T1) as well as a price-index number (
P1), we may likewise select as the form for Q
1 the median. In other words, the indexes for
p‘s and Q’s are best selected independently of each other. It is true we there by abandon any absolute mutual consistency between the two, but we are now speaking of practical, not theoretical, considerations.
One of the great practical advantages of the median is its use in conjunction with “quartiles” or “deciles” to portray
dispersion as well as averages. This method of showing dispersion about a mean is both easier to calculate, and capable of more detail, if detail be desired, than the method of Karl Pearson of the “Standard Deviation” about an arithmetical mean.
The final
practical conclusion, therefore, is that the weighted median serves the purposes of a practical barometer of prices, and also of quantities as well as, if not better than, formulæ theoretically superior.
In spite, however, of the peculiar simplicity and ease of
computation which characterizes the median, and in spite of Edgeworth’s strong indorsement, it remains still almost totally unused, if not unknown. Wesley C. Mitchell
*35 has used the median for price indexes more extensively than any one else. Professor Davis R. Dewey has used them for wages in his special Census report on that subject.
§9.
Summary
The conclusions of this Appendix may be briefly stated as follows:—
1. Any sum of products of two factors each, such as
SpQ, may be converted into any one of three forms: (1)
PT, in which
P is an average of the ratios of the
p‘s to some base
p0‘s, and
T is the quotient
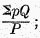
(2)
A Q, in which Q is an average of the ratios of the
Q‘s to some base
Q0‘s, and
A is the quotient
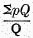 ;
;(3)
PQ
Sp0Q0.
2. Of the foregoing three formulæ only the last is symmetrical in the sense that the
p‘s and
Q‘s are treated alike.
3.
P and
T (or P and Q) are said to be
correlative, and any particular formula for either implies a particular correlative formula for the other.
4. Two correlative formulæ for
P and Q are, in general, quite unlike each other. If like formulæ be constructed for
P and Q, the correlate of Q constitutes a new formula for
P,said to be antithetical to the original formula for P, and
vice versa.
5. There are an indefinite number of formulæ for
P, of which 44 are given in the table; and there are at least 8 important tests to which each formula may conform in one of three degrees (1)
wholly, or for the ratio of
P1 to
P2, each being relative to a third year as a base; (2)
partially, or for the ratio
P1 to unity; and (3)
not at all.
6. The eight tests are of
proportionality as to prices or quantities (1 and 2);
determinateness as to prices or quantities (3 and 4);
withdrawal or entry as to prices and quantities (5 and 6); changing base as to prices and quantities (7); and changing units as to prices and quantities (8).
7. The tests arrange themselves in pairs, one of each pair relating to the
p‘s in the same manner as the other is related to the
Q‘s; but each test has significance both with respect to the
p‘s and the
Q‘s.
8. The formulæ arrange themselves in antithetical pairs.
9. Of any four neighboring compartments in the table, relating to two correlative rows (tests) and two antithetical columns (formulæ), the diagonals will have the same “scores.”
10. No known form of index number
P conforms perfectly to all the eight tests when a common base year is employed, but several conform well, the best being formula No. 11,
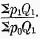
11. But if we are content with year-to-year comparisons, renouncing comparisons in terms of a third year, there are two formulæ which conform perfectly, viz. formulæ 17 and 21.
12. Practically, however, formula 11 is superior to 17 or 21, and formula 9 (median)—when properly “weighted”—is superior to 11.
13. For practical purposes, therefore, unless the expense and labor of computation can be disregarded, the median (with its two neighboring quartiles) is recommended, with a simple system of weights (whole numbers) based on expenditures, and changing from time to time for the sake of making better year-to-year comparisons.
Growth of Capital, London (George Bell and Sons), 1889, pp. 50-54, where allowance is made for changes in the price level. Index numbers of the
Economist, of Sauerbeck, and of Soetbeer are cited. Professor J. S. Nicholson has advocated such a capital-standard in the
Journal of the Royal Statistical Association, March, 1887, pp. 152 ff. This method is discussed by Edgeworth,
Report of the British Association, 1887, p. 276.
Measurement of General Exchange Value, New York (Macmillan), 1901, pp. 534, 553.
op. cit., pp. 81 and 82.
Berichte über die Verhandlungen der Königlich sächsischen Gesellschaft der Wissenschaften zu Leipsig; Mathematisch-physische Classe, Band XXIII, 1871, pp. 25-48). Also “Üeber die Berechnung der Veränderungen der Waarenpreise und des Geldwerthes” (
Jahrbücher für National-oekonomie und Statistik, 1871, Band XVI, pp. 143-156); and “Ueber einige Einwürfe gegen die in diesen Jahrbüchern veroffentlichte neue Methode, die Veränderungen der Waarenpreise und des Geldwerthes zu berechnen” (
ibid., 1871, Band XVI, pp. 416-427). See also Walsh,
op.cit., pp. 97-99, where the method is explained.
Report of the British Association for the Advancement of Science, 1889, p. 152. Sir Rawson-Rawson’s suggestion, as developed by Edgeworth, was to divide the value of exports (or imports) by the tonnage of exports (or imports) and consider the result as an index number of prices of exports (or imports). The suggestion was made not for any theoretical virtues, but because of the practical ease of computation. Edgeworth compares the results of Rawson’s rough and ready method with the more exact method of Giffen by actual figures for 1886 compared with 1885, and finds substantial agreement.
op.cit., p. 534.
Investigations in Currency and Finance, London (Macmillan), 1884; Edgeworth,
Reports British Association, 1887, 8, 9; Walsh,
op.cit., pp. 229 ff.
Reports British Association, 1887, 8, 9, esp. 1888, pp. 206 ff.
op.cit., p. 548.
op.cit., esp. pp. 191 ff., and pp. 539 ff.
op.cit.
Measurement of General Exchange-Value, pp. 386-388.
weights only makes an “error” one twentieth as great in the resultant index number, while an “error” in the
prices themselves makes an “error” in the resultant index number one fourth or fifth as great.
n” commodities is
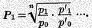
Evidently if
p1 becomes 0, the value of the entire expression becomes 0. If, therefore, we should depend on the geometric mean for ascertaining price levels, the temporary plethora of any commodity, to the extent of making its price vanish for a single moment, would cause the index number representing the entire price level for that moment to fall to 0. A form of average which in an extreme case is so absurd will
approach absurdity before the extreme is reached. Thus the geometrical average is unduly affected by prices which are low, even if not actually zero.
 ,
,fails to conform.
It is evident that if there is a change in the unit of any one commodity, such as that whose prices are
p1, and
p0, both the numerator and denominator will be affected, but not in the same proportion, except when it happens that

Consequently, the index number is dependent upon the unit of measurement. Such an index number is entirely arbitrary, and by sufficient manipulation of the units of measurement could be made to favor any particular commodity. The larger the unit of any particular commodity employed, the higher the price for it which enters into the formula, and the more that commodity tends to affect the result.
Bradstreet uses 96 commodities in common use, all of which are measured by the pound. The result is that silver, for instance, dominates over iron, entering at several dollars a pound instead of a few cents. If radium, which recently cost $8,000,000 an ounce, were included, it would absolutely dominate the group, and we would reach the absurd result that since radium has fallen to hundreds of thousands instead of millions of dollars an ounce, the general price level must have fallen several fold in spite of the general impression of rising prices! An index number of this kind is fitly called by Walsh one of accidental or haphazard weighting.
The easiest test to meet is test 8, opposite which the total is 40 out of 44; the next easiest is test 3 (and 4) with 31 out of 44.
Quarterly Journal of Economics, August, 1907, pp. 613-631.
Report of the British Association for the Advancement of Science, 1887, pp. 284-855.
ibid., pp. 284-286. From the standpoint, however, of the relation of prices to the currency, a large upward variation should count more than a small downward variation; for it requires more currency. In fact, as we have already seen, the arithmetical average complained of is precisely the average needed to fit into the equation of exchange. See § 6 of Appendix to Chapter II and § 7 of this Appendix. As to the asymmetry of price dispersion, see Mitchell,
Gold, Prices, and Wages under the Greenback Standard Berkeley (University of California Press), 1908, and reviews of same by Edgeworth,
Journal of the Royal Economic Society, December, 1908, pp. 578-582; and H. G. Brown,
Yale Review, May, 1909, pp. 99-101.
Philosophical Magazine, September, 1887; see also
Report of the British Association for the Advancement of Science, 1889, pp. 156-161, and
Journal of the Royal Statistical Society, June, 1888.
Report of the British Association for the Advancement of Science, 1888, pp. 208-211. Edgeworth compares various means for 21 articles in 1885 and 1873, one being that recommended by the committee of which he was a member, and above referred to in the text of Chapter X, §5.
relatively to 1860. There is practically no use in knowing the dispersion of prices in 1909 or 1910 as compared with 1860, and this knowledge throws no light on whether prices change uniformly or disperse widely from 1909 to 1910. What is needed is a knowledge of price dispersion from year to year, and this can readily be indicated by drawing three radiating lines from 1909 to 1910, the central one to show the movement of the median, and the other two to show the movements of the two neighboring quartiles.
Notes for Appendix to Chapter XII
