The Purchasing Power of Money
By Irving Fisher
THE purpose of this book is to set forth the principles determining the purchasing power of money and to apply those principles to the study of historical changes in that purchasing power, including in particular the recent change in “the cost of living,” which has aroused world-wide discussion.If the principles here advocated are correct, the purchasing power of money–or its reciprocal, the level of prices–depends exclusively on five definite factors: (1) the volume of money in circulation; (2) its velocity of circulation; (3) the volume of bank deposits subject to check; (4) its velocity; and (5) the volume of trade. Each of these five magnitudes is extremely definite, and their relation to the purchasing power of money is definitely expressed by an “equation of exchange.” In my opinion, the branch of economics which treats of these five regulators of purchasing power ought to be recognized and ultimately will be recognized as an exact science, capable of precise formulation, demonstration, and statistical verification…. [From the Preface to the First Edition]
First Pub. Date
1911
Publisher
New York: The Macmillan Co.
Pub. Date
1922
Comments
Assisted by Harry G. Brown (Instructor in Political Economy in Yale U.) 2nd edition. Harry G. Brown, assistant.
Copyright
The text of this edition is in the public domain.
- Preface to the First Edition
- Preface to the Second Edition
- Suggestions to Readers
- Addendum
- Chapter 1
- Chapter 2
- Chapter 3
- Chapter 4
- Chapter 5
- Chapter 6
- Chapter 7
- Chapter 8
- Chapter 9
- Chapter 10
- Chapter 11
- Chapter 12
- Chapter 13
- Appendix to Chapter II
- Appendix to Chapter III
- Appendix to Chapter V
- Appendix to Chapter VI
- Appendix to Chapter VII
- Appendix to Chapter VIII
- Appendix to Chapter X
- Appendix to Chapter XII
§ 1
CHAPTER XII
STATISTICS OF RECENT YEARS
THE last chapter was devoted to a brief sketch of price movements and their causes, in so far as the scanty data available make even a tentative interpretation possible. From this telescopic view of the past we turn to a microscopic view of the present. We shall confine it to a study of the events of the last three decades in the United States. In the study of the last chapter we found the facts of history to be in accord with the
a priori principles already set forth in the equation of exchange. But these facts of history were too general and vague to constitute a quantitative fulfillment of the equation of exchange. We shall find, however, much fuller data in the last few decades. We shall see that the equation of exchange, which has already been proved
a priori, may also be verified by actual statistics—within at least the limit of error to which the statistics are liable.
A good beginning of such a study is afforded by the pioneer work of Professor Kemmerer, already often referred to. He has estimated
*1 roughly the chief magnitudes of the equation of exchange and found that these conform in a general way to the conditions which the equation of exchange imposes. For each year, beginning
with 1879 (the year of resumption of the gold standard), and ending with 1908, he has estimated the total monetary and check circulation (what we have called
MV and
M‘
V‘) and the volume of trade (
T), and from these has calculated
*2 what the price level ought to be as determined by these factors,
i.e.
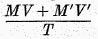
This calculated magnitude, which Professor Kemmerer calls the “relative circulation of money,” he then compares with the actual figures for price levels as given in statistics of index numbers.
Professor Kemmerer’s calculation is, I believe, the first serious attempt ever made to test statistically the so-called “quantity theory” of money. The results show a correspondence which is very surprising when we consider the exceedingly rough and fragmentary character of the data employed.
Most other writers who have attempted to test the quantity theory statistically seem to have been animated by a desire not to give it a fair test, but to disprove it. They have carefully avoided taking account of any factors except money and prices. It is not to be wondered at that they find little statistical correlation between these two factors.
*3 The virtue of Professor Kemmerer’s work consists in giving due attention to factors other than money.
The chief error in his investigation is the assumption of 47 as the velocity of circulation of money. The true value, as we shall see, is nearer 18 to 20. But the volume
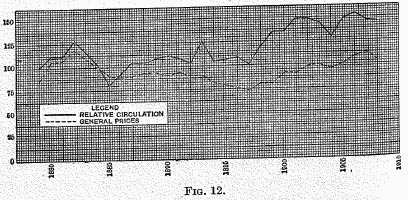
of money payments, even with Kemmerer’s exaggerated figure for velocity, is so small when compared with check payments, that this weakness does not greatly affect his final comparisons. At my request, Professor Kemmerer has recalculated his curves on the basis of 18 instead of 47 as the velocity of circulation of money. The results are given in Fig. 12. If these are compared with those contained in Professor Kemmerer’s book, there will be seen to be little difference. It is interesting to observe that when minute comparison is made the selection of 18 as the estimate of velocity gives a slightly better agreement between the two curves than does 47.
The “coefficient of correlation” between Professor Kemmerer’s results for
P, as directly shown by statistics and as indirectly calculated from the other factors in the equation of exchange, is found, by Professor Persons
*4 of Dartmouth, to be only .23 (or 23 per cent of perfect correlation), with a probable error of .13. As Professor Persons says, this is a very low degree of correlation.
But Persons’s method of testing agreement by means of a coefficient of correlation is not really applicable to two curves representing magnitudes changing
in time. For it practically ignores a most essential factor, their
order in time. A year-to-year comparison is better. If we consider the curves of prices and of “relative circulation,”
*5 we see at a glance that almost every successive change in direction in the one curve is matched by a corresponding change in direction in the other. In fact, out of 28 such possible coincidences, we find the actual number to be 16 cases of agreement in the changes of direction, 9 cases of disagreement, and 3 cases of a neutral kind (
i.e. cases which showed no change of direction in one of the two curves).
The above figures relate to the curves in Professor Kemmerer’s book. The later curves employing 18 instead of 47 for money-velocity show about the same results, there being 16 cases of agreement, 8 cases of disagreement, and 4 cases of a neutral kind. The correspondence here between prices and “relative circulation” is very slightly greater than before. In both sets of diagrams the agreements are not only much more numerous but much more pronounced than the disagreements.
Finally, some of the disagreements seem to be really agreements, disguised by being shifted forward one year. Thus, the inflections of 1899, 1900, 1901, for “relative circulation,” although all counted as cases of disagreement, are strikingly similar respectively to the inflections of 1900, 1901, 1902, for “general prices.” From the fact that the statistics are partly for calendar and partly for fiscal years, such one-year shifting of correspondence is to be expected, as Professor Kemmerer points out.
§ 2
I shall now attempt to make as precise statistical estimates of the magnitudes in the equation of exchange for the years 1896-1909 as the data available will allow. This period—1896-1909—is selected chiefly because its two end years afford the only known data making possible an estimate of velocity of circulation of money and of bank deposits.
The magnitudes will be considered in the order
M,M‘,
V‘,
V,T,P. For each the figures to be used are new.
M. The following table gives the estimated amount of money in circulation in the United States. By this we mean the total amount of money (coin and paper) outside of the federal treasury and outside the banks of deposit and discount (national, state, private and trust companies). The treasury stock is excluded because it is a hoard which does not become adjusted to needs of payment in the sense—or at any rate in the degree—that the stocks in merchants’ tills and in people’s pockets become adjusted. The bank reserves are excluded because, as we have shown, they are used for banking operations, not commercial purchases.
| ESTIMATED MONEY IN CIRCULATION IN THE UNITED STATES ( M) (IN BILLIONS OF DOLLARS) |
|||
|---|---|---|---|
| 1896 | .87 | 1903 | 1.38 |
| 1897 | .88 | 1904 | 1.37 |
| 1898 | .96 | 1905 | 1.45 |
| 1899 | 1.03 | 1906 | 1.59 |
| 1900 | 1.17 | 1907 | 1.63 |
| 1901 | 1.22 | 1908 | 1.63 |
| 1902 | 1.26 | 1909 | 1.63 |
This table is based on the official estimate of money in the United States, which includes money in banks and
in the federal treasury. These official figures are then corrected by means of recent revisions of the estimates of the gold in the United States, and by deducting the money in the federal treasury and the estimate of money in banks reporting and unreporting.
*6 The results differ somewhat from the official figures for so-called “money in circulation,” the chief reason for the discrepancy being that these official figures include money in banks. The figures here given are probably nearly correct; the probable error may, I believe, be assumed to be within 2 or 3 per cent.
The table shows that, during the space of thirteen years between 1896 and 1909, the money in circulation has nearly doubled and that its increase has been almost uninterrupted.
M‘. The following figures for
M‘ are estimates of
individual deposits, subject to check.
| INDIVIDUAL DEPOSITS SUBJECT TO CHECK ( M‘) *7 (IN BILLIONS OF DOLLARS) |
|||
|---|---|---|---|
| 1896 | 2.68 | 1903 | 5.70 |
| 1897 | 2.80 | 1904 | 5.80 |
| 1898 | 3.19 | 1905 | 6.54 |
| 1899 | 3.90 | 1906 | 6.84 |
| 1900 | 4.40 | 1907 | 7.13 |
| 1901 | 5.13 | 1908 | 6.60 |
| 1902 | 5.43 | 1909 | 6.75 |
These figures are based on the official figures for “individual deposits,” but are much less than these, owing to the fact that the official figures include deposits in savings banks and other deposits not subject to check, as well as to several other minor causes. The estimates here given constitute the first attempt to give a series
of figures for the bank deposits subject to check in the United States. It was made possible through the kind cooperation of the National Monetary Commission and its expert, Mr. A. Piatt Andrew.
*8
These figures give, therefore, the actual
deposit currency of the United States. They show an enormous growth of bank deposit currency. In the space of thirteen years (between the beginning and the end of the table) it has nearly trebled. Moreover, each year shows an advance over the preceding year, excepting only the year 1908 following the crisis of 1907.
§ 3
Having found
M and
M‘, the circulating media, we next proceed to ascertain
V and
V‘, their velocity of circulation. We shall find it convenient to consider the latter first.
The velocity of circulation of bank deposits is found by dividing respectively the total check circulation (
M‘
V‘) by the bank deposits (
M‘). The divisor,
M‘, has already been found. As to the dividend,
M‘
V‘, this is practically the total checks drawn in a year, for we may reasonably assume that, on the average, each check circulates against goods once and but once.
*9
For two years, 1896 and 1909, thanks to the efforts of Professor Kinley of the University of Illinois, we have voluminous and unique data collected originally for the purpose of calculating the ratio of money-transactions to check-transactions in the United States,
i.e. the ratio of
MV to
M‘
V‘. We shall see that these data, in conjunction with other official statistics, are sufficient for something more important than computing this ratio;
for they enable us to calculate with a tolerable degree of exactness the magnitudes
V and
V‘ for both the years mentioned. We shall find incidentally that, with the aid of these magnitudes, it is possible to work out more exactly than in the investigations above mentioned the very magnitude for which these investigations were undertaken, viz. the ratio of money-transactions to credit-transactions.
We need first to estimate
M‘
V‘.
M‘
V‘. Professor Kinley’s special investigation of 1896 indicates that on “the settling day nearest July 1, 1896,” the value of the checks deposited was about $468,000,000. If we could assume that this day was an average day for the year, we should need, in order to obtain the total year’s deposits of checks, simply to multiply this by the number of settling days in 1896, which was 305.
*10 But it happens that July 1 is an exceptionally heavy day in the deposit of checks. Making allowance for this fact, as indicated by the clearings of the New York clearing house, we conclude that the total year’s deposits of checks in 1896 was about 97 billions, with a probable error of some 5 or 6 per cent.
*11 Similar calculations for 1909 make the total check transactions of that year 364 billions.
*12 We have thus the value of the total check circulation (
M‘
V‘) in the two years 1896 and 1909, and find them to be 97 and 364 billions respectively, indicating a prodigious growth in thirteen years. We have still to interpolate figures for intervening years. For the period between these two years, we have, unfortunately, no such data as those of
Professor Kinley for 1896 and 1909. However, we can find an excellent barometer in the clearing house transactions,—a barometer dependent partly on the clearings in New York City, but more on those outside of New York City. It is well recognized that, although the clearings in New York deserve an exceedingly large representation, their relative importance in the total clearings is exaggerated.
*13
On the question, therefore, “What relative importance should be given respectively to clearings in New York and to the outside clearings in order to get the best barometer of the check transactions for the entire country?” we conclude that, if the outside clearings be multiplied by five and the result added to the New York clearings, we shall have a good barometer of check transactions for the United States.
*14
By means of this barometer of check transactions, consisting of New York clearings plus five times the outside clearings, and our knowledge of the actual check transactions of 1896 and 1909, we may easily derive from the “barometer” an estimate of the actual check transactions. The result is as follows:—
| ESTIMATED CHECK TRANSACTIONS ( M‘ V‘) (IN BILLIONS OF DOLLARS) 1896-1909 *15 |
|||
|---|---|---|---|
| 1896 | 97 | 1903 | 223 |
| 1897 | 106 | 1904 | 233 |
| 1898 | 127 | 1905 | 282 |
| 1899 | 166 | 1906 | 320 |
| 1900 | 165 | 1907 | 320 |
| 1901 | 208 | 1908 | 300 |
| 1902 | 222 | 1909 | 364 |
The probable error of the figures between 1896 and 1909 may be set at some 5 to 10 per cent.
V‘. Having obtained estimates of
M‘
V‘ and having previously obtained estimates of
M‘, it is easy, by simple division, to obtain
V‘. The results are as follows:—
| ESTIMATED VELOCITY ( V‘) OF CIRCULATION, BY CHECKS, OF DEPOSITS SUBJECT TO CHECK |
|||
|---|---|---|---|
| 1896 | 36 | 1903 | 39 |
| 1897 | 38 | 1904 | 40 |
| 1898 | 40 | 1905 | 43 |
| 1899 | 43 | 1906 | 47 |
| 1900 | 37 | 1907 | 45 |
| 1901 | 41 | 1908 | 46 |
| 1902 | 41 | 1909 | 54 |
The probable error in these figures may be set at some 5 to 10 per cent, being least for 1896 and 1909 and greatest midway between.
We note that the velocity of circulation has increased 50 per cent in thirteen years and that it has been subject to great variations from year to year. In 1899 and 1906 it reached maxima, immediately preceding crises. These results correspond to those of Pierre des Essars for the rates of turnover of deposits in continental banks already noted, except that he usually finds the maximum in the crisis year itself rather than the year before. It is to be noted that the figure for 1909 is much the highest in the table. Whether it portends an approaching crisis, time will determine.
§ 4
MV. Our next quest is for the velocity of circulation of money. The calculation of the velocity of circulation of money presents great difficulties,—difficulties which, in fact, have usually been considered insurmountable.
This opinion was well expressed by Jevons,
*16 who wrote:
“I have never met with any attempt to determine in any country the average rapidity of circulation, nor have I been able to think of any means whatever of approaching the investigation of the question, except in the inverse way. If we know the amount of exchanges effected, and the quantity of currency used, we might get by division the average number of times the currency is turned over; but the data, as already stated, are quite wanting”
As we shall see, however, data now exist, capable of revealing the “amount of exchanges effected,” or,
MV. In fact, this is equal to the total money deposited in banks, plus the total money-wages paid, plus a small miscellaneous item. From
MV and
M it is of course easy to obtain
V by division.
The formula for obtaining
MV is as simple as it may at first seem mysterious. The chief peculiarity of the method which this formula represents, and the feature which adapts it to practical use, is that it utilizes bank records and other ascertainable statistics as a means of discovering the total value of money transactions. The method is based on the idea that money in circulation and money in banks are not two independent reservoirs, but are constantly flowing from one into the other, and that the entrance and exit of money at banks, being a matter of record, may be made to reveal its circulation outside.
It is obvious how the bank-record would be read, were it true that every dollar withdrawn from banks circulated once and only once before being redeposited. Under these circumstances the annual flow of monetary circulation would exactly equal the annual withdrawal
from banks prior to circulation, as well as the annual deposits in banks subsequent to circulation.
Since we have a record of the first and last steps of the three, viz. the withdrawals and the deposits, we possess the means of knowing the intermediate step, the exchange of money for goods. The ordinary circulation of money,—excluding cases where it changes hands more than once between withdrawal and redeposit,—is equal to the money-flow through banks.
The complete facts, however, are not so simple, for the reason that money withdrawn from banks is often circulated more than once. Yet the complications involved follow definite laws. They do not destroy the value of the bank record, but merely make it somewhat more difficult to read. We propose to show (1) that in actual fact much money circulates out of bank only once, as in the hypothetical case just mentioned; (2) that when it is paid for wages, it usually circulates twice; and (3) that only rarely does it circulate three or more times before completing its circuit back to the banks.
This statement means that, like checks, money circulates in general only once outside of banks; but that when it passes through the hands of non-depositors (which practically means wage-earners) it circulates once more, thus adding the volume of wage payments to the volume of ordinary money circulation, which, as we have seen, is equal to the flow of money through banks.
We falsely picture the circulation of money in modern society when we allow ourselves to think of it as consisting of a perpetual succession of transfers from person to person. Were it such a succession, it would be, as Jevons said, beyond the reach of statistics. But we may form a truer picture by thinking of banks as the home of money, and the circulation of money as a temporary
excursion from that home. If this description be true, the circulation of money is not very different from the circulation of checks. Each performs one transaction or, at most, a few transactions, outside of the bank, and then returns home to report its circuit.
As is shown in the Appendix, the total money deposited in banks in 1896 amounted to nearly 10 billions of dollars,
*17 and the total expenditures of non-depositors to nearly 6 billions, of which 4½ billions constituted the expenditures of wage-earners; the remaining item in the formula for circulation amounted to less than 1 billion, making about 16 billions for the total circulation.
For 1909 the corresponding figures are: money deposited, 21 billions; expenditures of non-depositors, 13 billions; and the remaining item about 1 billion, making 35 billions in all.
The following table summarizes these results in billions of dollars:
*18—
| 1896 | 1909 | |
|---|---|---|
| 1st term (money deposited in banks) | 10- | 21 |
| 2d term (expenditure of “non-depositors”) | 6- | 13 |
| Remaining item | 1-
|
1
|
| TOTAL | 16+ | 35 |
V. In order to obtain the velocity of circulation, the total circulation,
MV (16 billions for 1896, or to be more exact, 16.2 billions), must be divided by the amount of money,
M, circulating in 1896. This amount is estimated at $870,000,000. Hence the velocity is 16,200,000,000 ÷ 870,000,000 = 18.6, or about 19 times a year. In other words, money was held on the average about 365 ÷ 19, which amounts to 19 or 20 days. If I have made as full allowance for error as I believe has been made, the error in this estimate does not exceed two or three days. For 1909 the velocity of circulation is estimated as the total circulation (35.1 billions) divided by the money in circulation (1.63 billions), which is 21.5+; that is, about 22 times a year, or once in 17 days. We conclude that the velocity of circulation of money in 1896 and the velocity in 1909 were about 19 and 22 times respectively, with a probable error judged to be about 2 in 1896 and not much more than 1 in 1909.
These results would assign money a slower circulation than most of the estimates or guesses which have been made. We must remember, however, that such persons as economists, who are most apt to think about the circulation of money, have a rapid turnover. They are usually city dwellers and the comparatively well to do, who, as we know, do not keep their cash inactive long. Laborers, especially thrifty laborers and laborers paid monthly, will keep cash on hand for several weeks without spending it. Farmers and others living in sparsely settled districts will even keep it for months. Probably the velocity of circulation of money differs widely among different classes and different localities.
We may now compare the years 1896 and 1909 in respect to money in circulation, deposit currency, their velocities, and their total circulation as follows:—
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| M | M‘ | V | V‘ | MV | M‘ V‘ |
MV + M‘ V‘ |
|
| 1896 | .87 | 2.68 | 19 | 36 | 16 | 97 | 113 |
| 1909 | 1.63 | 6.75 | 22 | 54 | 35 | 364 | 399 |
Our next task is to interpolate estimates for
V between 19 in 1896 and 22 in 1909. The results are given in the following table:—
| ESTIMATES OF V, 1896 to 1909 *19 |
|||
|---|---|---|---|
| 1896 | 19 | 1903 | 21 |
| 1897 | 19 | 1904 | 21 |
| 1898 | 20 | 1905 | 22 |
| 1899 | 22 | 1906 | 22 |
| 1900 | 20 | 1907 | 21 |
| 1901 | 22 | 1908 | 20 |
| 1902 | 22 | 1909 | 22 |
§ 5
We have now finished our statistical review of the magnitudes
M,M‘,
V,V‘, on the left side of the equation of exchange, and have remaining only the two magnitudes
P,T, on the right side of the equation.
First we shall consider
T. The results of our calculations are given in the following table, which expresses the volume of trade in billions of dollars as reckoned at the prices of 1909:—
| ESTIMATED VOLUME OF TRADE (IN BILLIONS OF DOLLARS AT PRICES OF 1909) | |||
|---|---|---|---|
| 1896 | 209 | 1903 | 335 |
| 1897 | 239 | 1904 | 324 |
| 1898 | 260 | 1905 | 378 |
| 1899 | 273 | 1906 | 396 |
| 1900 | 275 | 1907 | 412 |
| 1901 | 311 | 1908 | 381 |
| 1902 | 304 | 1909 | 399 |
The table is constructed by averaging the index numbers of the
quantities (not the values) of trade in various lines. The figures representing trade are based on data for 44 articles of internal commerce, 23 articles of import and 25 of export, sales of stocks, railroad freight carried, and letters through the post office. The final figures are so adjusted that the figure for 1909 shall be 399; namely, the actual money value of transactions in that year as worked out on the other side of the equation (
i.e.MV +
M‘
V‘). Relatively to each other, the numbers for
T are independent of the other side of the equation.
*20
P. The only remaining factor in the equation of exchange is the index number of prices,
P. Theoretically this could be calculated from the other five magnitudes already evaluated, provided all our
previous calculations could be depended upon for absolute accuracy. But there are possible errors in all the magnitudes
M,M‘,
V,V‘,
T, and such errors, should they exist, would be registered cumulatively in
P. It is important, therefore, to check such an indirectly calculated value of
P by directly calculated statistics. By so doing we are able to compare the
P directly calculated and the
P indirectly calculated. In like manner, we might, if desired, compare the directly and indirectly calculated values of
M,M‘,
V,V‘, and
T. We shall confine ourselves to comparing the two values of
P, since it is
P which, as we have seen, is really dependent on the five other factors in the equation of exchange. The values of
P (including prices of commodities, securities, and labor), directly calculated in terms of the figures for 1909, as 100 per cent, are as follows:—
| INDEX NUMBERS OF GENERAL PRICES | |||
|---|---|---|---|
| 1896 | 63 | 1903 | 87 |
| 1897 | 64 | 1904 | 85 |
| 1898 | 66 | 1905 | 91 |
| 1899 | 74 | 1906 | 96 |
| 1900 | 80 | 1907 | 97 |
| 1901 | 84 | 1908 | 92 |
| 1902 | 89 | 1909 | 100 |
This table is based on the figures of the Bureau of Labor for wholesale prices. It differs slightly from the Bureau of Labor figures owing to the fact that we here include prices of securities and wages.
*21
It remains to compare these actual statistics for
P with
P as computed indirectly from the other magnitudes in the equation of exchange. This calculation and comparison will be given in the following section.
§ 6
We have now calculated independently the six magnitudes of the equation of exchange for the fourteen years 1896-1909. But, as already stated, we know that these six magnitudes are mutually related through the equation of exchange. The question arises whether the magnitudes as calculated will actually fulfill approximately the equation of exchange.
One way of testing this question is that adopted by Professor Kemmerer; namely, to compare the statistics for any one factor (say
P), as above directly calculated, with what it would be as indirectly calculated from the five other magnitudes in the equation of exchange. The following table shows the value of
P as obtained in these two ways:—
| INDEX NUMBERS OF PRICES AS CALCULATED | ||
|---|---|---|
| DIRECTLY ( P) |
INDIRECTLY |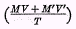
|
| 1896 | 63 | 54 |
| 1897 | 64 | 52 |
| 1898 | 66 | 56 |
| 1899 | 74 | 69 |
| 1900 | 80 | 68 |
| 1901 | 84 | 76 |
| 1902 | 89 | 82 |
| 1903 | 87 | 75 |
| 1904 | 85 | 81 |
| 1905 | 91 | 83 |
| 1906 | 97 | 90 |
| 1907 | 97 | 86 |
| 1908 | 92 | 87 |
| 1909 | 100 | 100 |
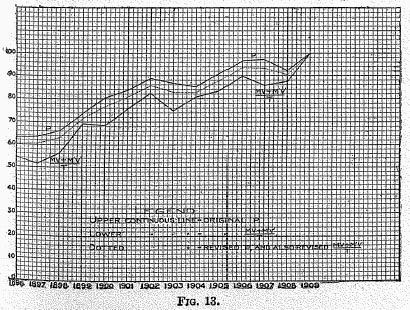
The agreement between the two sets of figures is visualized in Figure 13.
The two values as shown by the upper and lower
curves agree with each other remarkably well.
*22 The closeness of their agreement may be expressed in several ways. One way is to count the agreements and disagreements in their changes of direction or inflections. Out of 12 inflections in each curve the two agree six times, disagree three times, and are neutral three times. Another method is that employed by Professor Pearson. This method consists in calculating what Professor Pearson calls a “correlation coefficient.” It shows an agreement of 97 per cent of perfection as compared with 23 per cent which Professor Persons of Dartmouth found for Professor Kemmerer’s figures
*23 for 1879-1901. But, as already stated, a coefficient of correlation for
successive data is apt to be misleading. If, in the case of Professor Kemmerer’s figures, the coefficient .23 was an understatement of the parallelism between his curves, the coefficient .97 overstates the parallelism between mine. This overstatement is always likely to result when both of the curves to be compared rapidly ascend or descend.
*24
The proper method of applying a coefficient of correlation to successive data appears to be to calculate
the coefficient, not for the raw figures, but for their successive year-to-year ratios. In other words, we tabulate and compare the ratios of each year’s
P to the preceding year’s
P and of each year’s
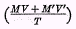to the preceding year’s
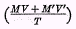. If the two sets of ratios should rise or fall together, the curves would show a close parallelism or agreement in their successive changes of direction. As a matter of fact, the results of this method show a coefficient of correlation of 57 per cent (or .57 ± .10, where .10 is the probable error). This figure, 57 per cent, is a moderately high coefficient of correlation.
*25 We may conclude, therefore, that the “quantity theory” is statistically verified to a high degree of correlation.
*26
It is to be emphasized that the coefficients of correlation as just given compare the price level with what it should be according to the statistics of the
five magnitudes on which, by the so-called quantity theory, it is dependent. The correlation would be less if instead of these five magnitudes only
one were taken. Thus the coefficient of correlation for 1896-1909 as between money,
M, and prices,
P, by the year-to-year-ratio
method is 43 per cent (or .43 ± .13).
*27 Even this is a moderately high degree of correlation.
If the opponents of the “quantity theory” who attempt to disprove any relation between money and prices by pointing out the lack of statistical correspondence between the two mean merely that other factors besides money,
M‘,
V,V‘,
T, change from time to time and that therefore the level of prices does not in actual fact vary exactly with the quantity of money, their contention is sound. But the proposition involved is of as little scientific consequence as the proposition that the pressure of the atmosphere does not vary from day to day in exact proportion to its density. We know that, temperature being constant, the pressure of a gas varies directly as its density; but that, as a matter of fact, temperature seldom is constant. Any critic of Boyle’s law who should attempt to dispute its validity on such a ground, however, would merely betray his ignorance of the real meaning of a scientific law; and if he should seriously attempt to “disprove it statistically” by plotting daily curves of barometric pressure and atmospheric density, he would subject himself to scientific ridicule.
If any one has ever really imagined that the price level depends solely on the quantity of money, he should certainly be corrected. But the really important matter is that students of economics should appreciate the existence of a
law of direct proportion between quantity of money and price level—a law as real, as important, and as fundamental in the economic theory of money, as Boyle’s law of direct proportion between density and pressure is real, is important, and is fundamental
in the physical theory of gases. I believe that the frequent failure to realize the existence of this law is due largely to the lack of any clear conception of the magnitudes involved.
M and
P seem to be the only magnitudes which some students really understand.
M‘,
V,V‘,
T are seldom discussed or even mentioned. But not until the subject is put on a statistical basis,—in figures which measure actual deposit currency, velocities of circulation, and volume of trade,—will these magnitudes be recognized as having a real existence and significance.
But, to a candid mind, the quantity theory, in the sense in which we have taken it, ought to appear sufficiently secure without such checking. Its best proof must always be
a priori, not in the sense which applies to the proof of abstract mathematical propositions, but in the sense which applies to the proof of Boyle’s law. Thus, it is known by induction that the pressure of a confined gas is caused by the bombardment of its molecules on the containing walls. It is likewise known by induction that the pressure must be proportional to the frequency of impact, provided the velocities of the molecules are constant. Finally, it is known that frequency of impact must be proportional to the number of molecules,
i.e. the density of the gas, and that constancy of velocity implies constancy of temperature. Therefore, it follows that, temperature being constant, pressure is proportional to density. Thus, from knowledge gained inductively of the individual pressures of the molecules which compose the gas, we may reason out
deductively the general pressure of a gas.
Analogously, from knowledge gained inductively of individual exchanges—molecules as it were—which
compose society’s exchange, we may reason out deductively the general equation of exchange.
Fortunately, just as Boyle’s law has been established both deductively and inductively, we may now assert that the equation of exchange has been sufficiently established both deductively and inductively.
As previously remarked, to establish the equation of exchange is not completely to establish the quantity theory of money, for the equation does not reveal which factors are causes and which effects. But this question has been answered in Chapter VIII.
§ 7
To those who have faith in the
a priori proof of the equation of exchange the real significance of the remarkable agreement in our statistical results should be understood as a confirmation, not of the equation by the figures, but of the figures by the equation. There are discrepancies in our inductive verification; but these are all well within the limit of errors of measurement. The discrepancies prove that slight errors exist among the figures; otherwise, they would conform exactly to the relation prescribed by the equation of exchange.
Our next task is to examine the discrepancies and locate, so far as possible, the errors involved. The degree of total mutual discrepancy between the independently calculated magnitudes is best expressed by the degree of inequality between the calculated values of
MV +
M‘
V‘ and
PT, which
should be equal. That is,
PT divided by
MV +
M‘
V‘ should always be unity. Actual division gives the figures in the column headed “original” in the following table. The other column will be explained presently.
| RATIO OF PT TO MV + M‘ V‘ AS CALCULATED |
||
|---|---|---|
(1) |
ORIGINAL (2) |
REDUCED (3) |
| 1896 | 1.17 | 1.06 |
| 1897 | 1.24 | 1.13 |
| 1898 | 1.18 | 1.07 |
| 1899 | 1.06 | .95 |
| 1900 | 1.17 | 1.06 |
| 1901 | 1.11 | 1.00 |
| 1902 | 1.08 | .97 |
| 1903 | 1.16 | 1.05 |
| 1904 | 1.06 | .95 |
| 1905 | 1.09 | .98 |
| 1906 | 1.08 | .97 |
| 1907 | 1.13 | 1.02 |
| 1908 | 1.05 | .94 |
| 1909 | 1.00 | .89 |
The figures in column (2) show that the calculated values of
PT are always larger than the calculated values of
MV +
M‘
V‘, the excess varying from 24 per cent to 0 and averaging 11 per cent.
But these discrepancies between
PT and
MV +
M‘
V‘ can be substantially diminished merely by changing the base for measuring prices. This base we have thus far taken as the price level of 1909. But as the index numbers have only a relative significance, we are free to choose any other set of numbers so long as they maintain the same
relative magnitudes. In accordance with this prerogative we choose to reduce all the numbers for
P by 11 per cent, this being the average of the original discrepancies. The result will be to decrease
PT by 11 per cent and to change the series of discrepancies from those shown in column (2) to (approximately) those shown in column (3). These numbers vary from 13 per cent above to 11 per cent below unity. These errors
are very small—far smaller in fact than might have been expected in view of the incomplete and unreliable character of some of our data.
The question remains, Where shall we place the blame for the errors which the small existing discrepancies indicate? Is the fault with
M,M‘,
V,V‘,
P, or
T? How shall we correct our calculated figures? We may conclude on general principles that the smallest corrections are the most likely to be right. The smallest corrections imply a
mutual adjustment between the six factors, each adjustment being in the direction which will diminish the existing discrepancy. In this way each factor, as calculated, is regarded as having
some value, and is given some influence in correcting the
others; so that any one factor requires extremely little change. The changes made in the various factors are made in proportion to their assumed relative liability to error.
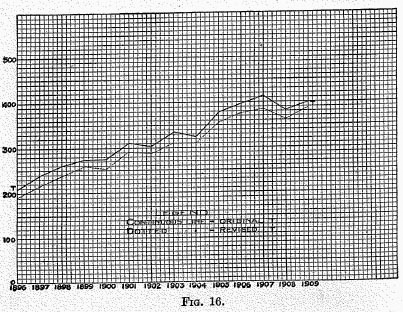
The results are shown in Figures 14, 15, 16, and the previous Figure 13, each of which relates to one of the factors in the equation of exchange as originally calculated and as finally adjusted (dotted lines). When they are all thus adjusted, they conform exactly to the equation of exchange.
*28
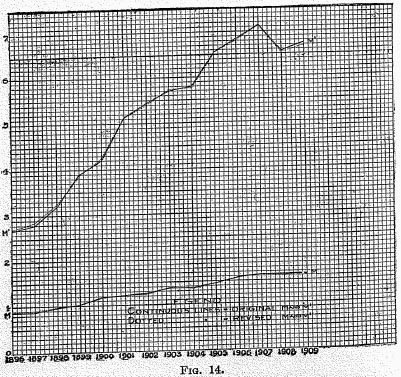
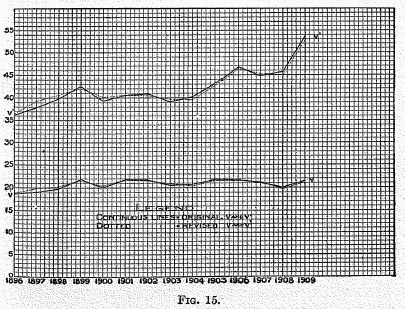
In Figure 14 we see that the alterations made in the figures for
M and
M‘ are so trifling as to be almost negligible, being usually much less than 1 per cent. The alterations in
V and
V‘, which are shown in Figure 15, though somewhat greater, are also small, being usually
less than 2 per cent. The alterations in
T, as shown in Figure 16, though still greater than the preceding, are nevertheless so small and uniform as to preserve an almost perfect parallelism between the original and the altered curve. The differences rarely exceed 10 per cent. The alterations in
P are shown in the previous Figure 13, the upper curve representing the original and the dotted, or middle, curve representing the altered figures for
P. Here also an extremely close parallelism between the original and the altered curves is evident. The differences rarely exceed 3 per cent.
Certainly the most exacting of critics could not ask for any greater consistency of results and conformity to the theory of the equation of exchange than these statistics show. The corrections which have been found necessary to bring the six figures as first calculated into perfect agreement are smaller than the probable error
in those figures themselves. I had—quite antecedently to any knowledge of how closely the final results would harmonize—assigned certain rough estimates of the probable errors. These are noted in the Appendix. The probable error of
M is adjudged to be 2 or 3 per cent; of
M‘, 2 or 3 per cent; of
V, 5 to 10 per cent; of
V‘, 5 to 10 per cent; of
P, 5 to 10 per cent; and of
T, 5 to 10 per cent. In other words, our statistical data were regarded as only rough or approximate; yet the final “doctoring” needed to make them agree with each other was, as has been seen, seldom over 2 per cent, being less than 1 per cent for
M and
M‘; less than 2 per cent for
V and
V‘; less than 3 per cent for
P; and less than 4 per cent for
T. We conclude then that the figures fit each other better than might be expected from their known lack of precision.
The corrections which we have assigned to the various factors are so insignificant that it would be hazardous to attempt to explain them specifically. The errors which they presumably represent might be due to numerous sources, such as the varying ingredient in the New York clearing house transactions of bank transfers as distinct from ordinary check transactions; or such as errors or defects in the statistics of trade in grain, etc.; or such as an over or underestimate of the deviation from normal of the particular days in 1896 and 1909 on which the statistics of deposits made in banks were gathered; or such as over or underestimates of the unreported deposits, or over or underestimates of the gold in the United States, or over or underestimates of wages and of other numerous minor though often conjectural elements in our calculations.
The sources of error just mentioned were named in the order of their probable importance. It is, perhaps, significant that the greatest discrepancies are in
the years 1896-1898, whose data for
T were most defective, and in 1900, 1903, and 1907, which were years of crises or of impending crises.
§ 8
After making the above named mutual adjustments among the six magnitudes in the equation of exchange, we reach the following figures, constituting our final table of values for
M,M‘,
V,V‘,
P, and
T; they are the figures plotted in the dotted curves above given:—
| FINALLY ADJUSTED VALUES OF ELEMENTS OF EQUATION OF EXCHANGE (AS TO 1910-1912, SEE P.492) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| M | M‘ | V | V‘ | P | T | MV | M‘ V‘ |
MV + M‘ V‘ & PT |
|
| 1896 | .88 | 2.71 | 18.8 | 36.6 | 60.3 | 191 | 16 | 99 | 115 |
| 1897 | .90 | 2.86 | 19.9 | 39.4 | 60.4 | 215 | 18 | 112 | 130 |
| 1898 | .97 | 3.22 | 20.2 | 40.6 | 63.2 | 237 | 20- | 131- | 150 |
| 1899 | 1.03 | 3.88 | 21.5 | 42.0 | 71.6 | 259 | 22 | 163 | 185 |
| 1900 | 1.18 | 4.44 | 20.4 | 38.3 | 76.5 | 253 | 24 | 170 | 194 |
| 1901 | 1.22 | 5.13 | 21.8 | 40.6 | 80.5 | 291 | 27 | 208 | 235 |
| 1902 | 1.25 | 5.40 | 21.6 | 40.5 | 85.7 | 287 | 27 | 219 | 246 |
| 1903 | 1.39 | 5.73 | 20.9 | 39.7 | 82.6 | 310 | 29 | 227 | 256 |
| 1904 | 1.36 | 5.77 | 20.4 | 39.6 | 82.6 | 310 | 28 | 228 | 256 |
| 1905 | 1.45 | 6.54 | 21.6 | 42.7 | 87.7 | 355 | 31+ | 279+ | 311 |
| 1906 | 1.58 | 6.81 | 21.5 | 46.3 | 93.2 | 375 | 34 | 315 | 349 |
| 1907 | 1.63 | 7.13 | 21.3 | 45.3 | 93.2 | 384 | 35 | 323 | 358 |
| 1908 | 1.62 | 6.57 | 19.7 | 44.8 | 90.3 | 361 | 32 | 294 | 326 |
| 1909 | 1.61 | 6.68 | 21.1 | 52.8 | 100.0 | 387 | 34 | 353 | 387 |
| 1910 | 1.69 | 7.23 | 21. | 52.7 | 104.0 | 399 | 34 | 381 | 415 |
| 1911 | 1.64 | 7.78 | 21. | 49.9 | 102.2 | 413 | 34 | 388 | 422 |
| 1912 | 1.71 | 8.17 | 22. | 53.4 | 105.3 | 450 | 38 | 436 | 474 |
This table, combining as it does the virtues of all the independent calculations of
M,M‘,
V,V‘,
P,T, with the corrections of each necessary to make it conform to the others, may be considered to give the best available data concerning these magnitudes.
These figures, or the dotted curves in the preceding diagram, show that money in circulation (
M) has nearly
doubled in thirteen years; that its velocity of circulation (
V) has increased only 10 per cent; that the deposit currency has nearly tripled and its velocity of circulation (
V‘) has increased 50 per cent; that the volume of trade has doubled; and that prices have risen two thirds.
These results are not surprising, but are, I believe, just such as we might expect. Nevertheless, almost all are new. The figures for money in circulation (
M) are not greatly different from those given in official documents and used by Professor Kemmerer. Likewise the figures for index numbers of prices are based chiefly on, and are very similar to, the index numbers for wholesale prices of the United States Labor Bureau. The statistics for volume of trade are constructed entirely anew and differ somewhat from Kemmerer’s, which were their only precursors. The statistics for deposits subject to check (M’) are here published for the first time. The statistics of velocities of circulation of bank deposits (
V‘) are the first statistics of their kind, excepting the statistics for the activity of bank accounts of European Banks. Finally the statistics of velocity of circulation of money (
V) are the first of their kind.
With these data we are able to form a fairly correct statistical picture of the circulatory system in the United States. According to the records of 1909, the money in actual circulation (
M) is 1.6 billions of dollars or $18 per capita (much less than the official figure given for circulation, $35); its velocity of circulation (
V) is twenty-one times a year; the deposit currency (
M‘) is 6.7 billions or $74 per capita—fourfold that of money; its velocity of circulation (
V‘), 53 times a year—two and a half times that of money; the total circulation of, or payments by, money (
MV), 34 billions a year; the circulation
of deposits subject to check or payments by check (
M‘
V‘), 353 billions—ten times as much or nearly a billion a day. This makes a grand total for business done at present prices (
MV +
M‘
V‘ or
PT) of 387 billions, or more than a billion a day. The size of this aggregate will probably astonish most readers. In the absence of actual statistics we have heretofore little realized the colossal proportions of our trade. Probably few persons outside of statisticians would have imagined that our import and export trade, which has filled so large a place in our political vision, sinks into utter insignificance as compared with the internal trade of the country. The total exports and imports amount only to a paltry 3 billions as compared with a total national trade of 387 billions.
We are now ready to represent the entire set of figures given in the last table by means of the mechanical illustration adopted in previous chapters. This is done in Figure 17, which shows at a glance the course of all the six magnitudes for fourteen years, making 84 statistical figures in all. This mechanical picture visualizes the increase in prices (lengthening in right arm) which has been going on during these fourteen years, and at the same time exhibits the changes in all the five factors on which that increase of prices depends. All of the six magnitudes represented are, of course, the
corrected ones, so as to exactly harmonize with each other and make the two sides of the scales balance. The steady growth of the money in circulation is shown in the increase in the size of the hanging purse; the similar but more rapid growth of deposits subject to check is shown by the increase in the size of the bank book; the lesser growth in the velocities of these two media of exchange is shown by the lengthening of the two arms at the left
of the fulcrum. These four factors have all conspired to increase prices. The only cause resisting the rise is the growth of trade, which is shown by the increasing size of the hanging tray at the right and which has tended to reduce prices.
We have here a complete quantitative picture of the causes affecting the price level during the last fourteen years, or, at any rate, of all the
proximate causes; for, as we have noted, back of the five proximate causes lie innumerable antecedent causes.
What then, in brief, are the facts of history? They are that prices have increased by about two thirds between 1896 and 1909, that this has been
in spite of a doubling in the volume of trade, and
because of (1) a doubling of money, (2) a tripling of deposits, and (3 and 4) slight increases in the velocities of circulation.
§ 9
There has been much discussion as to the most important causes which have increased prices during recent years. It is, therefore, interesting to compare the four proximate causes which, as we have seen, have alone tended to increase prices in the period 1896-1909. Perhaps the simplest and best method is to compare the actual rise of prices with what it
would have been if any one cause of that rise had been absent. That is, we test the importance of any price-raising factor by answering the question, What difference does it make to prices whether that factor is present or absent? We shall find that the growth of money is by far the most important cause. The growth of deposits is less important than appears at first glance. The growth of deposits would have to be regarded as the most important cause if deposits could be considered as independent of money.
But they are not independent. We have seen that, normally, deposits rise or fall with money in circulation. Therefore, if deposits had increased just as fast as money and no faster, we should ascribe the whole increase to money alone. In that case no part of the rise of prices would be ascribable to any increase in deposits; for there would have been no increase except what was due to the increase in money. The increase of deposits subject to check can be considered independently of the increase of money only in so far as the deposits have increased
relatively to money. We have seen that mere increase of money would of itself normally cause a proportionate increase of deposits; only the
disproportionate increase of deposits should therefore be considered apart from the increase in money as a cause of rising prices. Therefore the true method of considering deposits as a separate cause appears to be to reckon them relatively to money. That is, not
M‘, but
M‘/
M is the magnitude to be considered.
*29
We may therefore consider as the only causes tending to raise prices during the period 1896-1909, the following four:—
(1) The increase in money in circulation,
i.e. the increase in
M.
(2) The increase in relative deposits,
i.e. the increase in
M‘/
M.
(3) The increase in the velocity of circulation of money,
i.e. the increase in
V.
(4) The increase in the velocity of circulation of deposits,
i.e. the increase in
V‘.
The fifth factor determining the price level, viz. the factor
T has, as we have seen, tended to
lower prices.
We shall now proceed to note what would be the
separate effects on prices of these four price-raising causes and of the one price-depressing cause.
We wish, then, to know what the price level
would have been in 1909 under the following five conditions:—
(1) If the money in circulation (
M) had not grown at all since 1896,
(2) If the relative deposits
M‘/
M had not grown at all since 1896,
(3) If the velocity of circulation of money (
V) had not grown at all since 1896,
(4) If the velocity of circulation of deposits (
V‘) had not grown at all since 1896,
(5) If the volume of trade (
T) had not grown at all since 1896,
assuming in each case that all the other four factors had grown in exactly the way they did grow. We have taken the actual price level in 1909 as 100 per cent and shall continue to do so, expressing on this basis what the price level
would have been under each of the five hypotheses above named. We reach the following results:
*30—
Were it not for the growth of
(1) Money (
M), the price level of 1909 would have been 55 instead of 100;
(2) Relative deposits (
M‘/
M), the price level of 1909 would have been 77 instead of 100;
(3) Velocity of circulation of money (
V), the price level of 1909 would have been 99 instead of 100;
(4) Velocity of circulation of deposits (
V‘), the price level of 1909 would have been 72 instead of 100;
(5) Volume of trade (
T), the price level of 1909 would have been 206 instead of 100.
In other words, were it not for the growth of
(1) Money (
M), prices would have been 45 per cent lower;
(2) Relative deposits (
M‘/
M), prices would have been 23 per cent lower;
(3) Velocity of money (
V), prices would have been 1 per cent lower;
(4) Velocity of deposits (
V‘), prices would have been 28 per cent lower.
(5) Volume of trade (
T), prices would have been 106 per cent higher.
The four price-raising causes may, therefore, be arranged in the following order of relative importance:—
Except for the growth of
V, prices would have been 1 per cent lower than they were.
Except for the growth of
M‘/
M, prices would have been 23 per cent lower than they were.
Except for the growth of
V‘, prices would have been 28 per cent lower than they were.
Except for the growth of
M, prices would have been 45 per cent lower than they were.
We conclude, therefore, that the growth of the velocity of circulation of money was a negligible factor in raising prices; that the relative growth of deposits and their velocity were large factors; and that the growth of money was the largest. The importance of the growth of money as a price-raising factor was, according to the above figures, almost exactly double that of relative deposits and a little over 50 per cent greater than that of their velocity of circulation.
§ 10
But the full effect of the increase in the quantity of money is really greater even than these figures indicate; for we have not included the effect of the overflow of money abroad, caused by the great increase in American bank deposits. Evidently this overflow must be taken into account; for the other three price-raising factors, by crowding out money and usurping its place, have given themselves an exaggerated appearance of importance. In other words, there has been a greater increase in money than appears from the United States figures by the amount which has overflowed into foreign lands. The United States is only a small part of the world’s market, and its price level is largely determined by the world’s price level. Whatever raises prices in one country tends to raise prices in all countries, and in the last analysis the only correct way to measure the relative importance of price-raising causes is to consider the world as a whole. If the statistics we have worked out for the United States were typical of the world, the resulting estimate of the relative importance of the four price-raising causes would be true of the world.
But there is strong reason to believe that the growth of deposits and of their velocity played a far greater part in raising prices in the United States than anywhere else. The reason is that banking is in its infancy in France and most other countries. It is so unimportant that even if its rate of growth there were prodigious, it would still be a relatively insignificant price-raising factor. We may therefore be certain, humanly speaking, that outside of the United States the increase of prices is even more largely due to the growth of money (gold) than in the United States.
We conclude, therefore, with much confidence, that the increase in the world’s gold is chiefly responsible for the increase in the world’s prices. What has been said probably explains why, in the last three years, there has been no actual increase in the quantity of money in circulation in the United States. It has been crowded out or prevented from increasing by the excessively great increase of our deposits and of their velocity of circulation.
But besides the world movements of prices there are special local movements as well. Anything which interferes with trade, like a tariff, tends to make the rise of prices unequal. There remains, therefore, the question of such
special influences on the American price level as the tariff,—working out its effects through
M.
As we have seen in a previous chapter, the effect of enacting a protective tariff is to raise the price level of the “protected” country by creating temporarily a “favorable” balance of trade and thus stimulating imports of the money metal and discouraging its export. This effect ceases as soon as the price level at home has been elevated enough, relatively to the price levels abroad, to restore the equilibrium of trade and stop the relative
accumulation of gold in the protected country. Thereafter the tariff ceases to affect the price level, except as it interferes with trade and thereby prevents the price level at home from adjusting itself to the price levels abroad. This
interfering effect may be in either direction; that is, the price level at home will be rendered more
independent of foreign price levels than it would be if trade were free. The tariff merely
isolates the protected country.
During the period under investigation, 1896-1909, there have been two changes in the tariff, that of 1897, and the more recent law of 1909. The first represented an advance over the rates of 1894. This law of 1897 must have tended, therefore, somewhat to restrict imports and to raise prices. So far as our prices have risen faster than prices have risen in other countries, like England, in the period here considered, it seems fair to attribute a part of this additional rise to our tariff system.
We come finally to the tariff of 1909. This act is so recent as scarcely yet to have had much perceptible influence, even if that influence be assumed to have begun as soon as the act was planned, early in 1909. There has waged a bitter political controversy over the question whether it was a revision upward or downward. The best unbiased opinion seems to be that it was slightly upward but was chiefly a mere rearrangement by which some duties were raised and others lowered. These conclusions of Professor Taussig, Professor Willis, and others are based on an intensive study of the tariff schedules.
A review of the statistics of the equation of exchange is entirely consistent with these conclusions. This consistency may not be evident at first glance. On the contrary,
those who claim that duties have been greatly increased might point to the fact that since the tariff American prices have risen faster than English prices;
*31 while those who claim that the revision was distinctly downward might point to the increase in our imports of commodities, and the increase in our exports of gold. But these seemingly discordant facts are reconcilable.
American statistics show that there has been an enormous expansion in bank deposits and in their velocity of circulation in 1909 as compared with 1908. This would naturally have the effect of raising American prices, displacing gold, and checking the increase of money in circulation in the United States, which would otherwise occur, and correspondingly of encouraging the import of commodities. The facts agree precisely with these known tendencies. Prices in the United States have risen more than in England, the increase in the quantity of money in circulation has been checked, the export of gold and the import of commodities have been increased. Thus we may explain all the facts without assuming the tariff as a disturbing element.
*32
It would take us too far afield to discuss all the other factors which have been held more or less responsible for the increase in prices. We have already made it clear
that none of these could influence prices except by increasing the quantity of money in circulation, the relative deposits, or their velocities, or by decreasing trade. As trade has increased greatly, the last possibility may be ignored.
As to the causes which have increased money and deposits and their velocities, the most important seem to be the following:—
(1) The chief cause of the increase of money has been the increase in gold mining. Bank notes have only slightly more than kept pace with other money in circulation.
(2) The chief causes of the relative increase in bank deposits seem to have been those which have extended banking especially in the South. The recent banking laws, encouraging the establishment of small banks, may have had some part in this extension.
(3) The chief cause of the increase of velocity of circulation, especially of bank deposits, seems to have been the concentration of population in cities. We have seen that the larger the town the greater the velocity of circulation of bank deposits.
§ 11
Throughout this book we have aimed at explaining the
general purchasing power of money, not its purchasing power over any particular goods or class of goods. The problem of the rise in “the cost of living” is partly a
general problem of the purchasing power of money, and partly a
special problem of the prices of food, clothing and other costs of “living.” With the special problem we have here nothing to do. But it so happens that the special changes in the cost of living are very small as compared with the general change in
prices. At any rate this is true of the wholesale prices of food. The index number of food rose between January, 1909, and March, 1910, from 122.6 to 130.9, while general wholesale prices rose from 124.0 to 133.8; that is, the special prices of food rose about evenly with the general rising tide of prices. So far as there was any difference it was such that the special prices rose slightly less than general prices. The “general prices” here referred to are only wholesale prices and do not include prices of labor and securities; but the inclusion of these elements, judging from the statistics as already given up to 1909, and market reports since that date, would not materially change the result.
We conclude that the “rise in the cost of living” is no
special movement of food prices nor, presumably, of other particular prices, but is merely a part of the general movement of prices. The cost of living is swept along with the general rising tide of prices of all sorts. It indicates little or no special change in the supply or demand of special classes of goods, but simply reflects the fall in the general purchasing power of money. These remarks apply not simply to the months beginning with January, 1909, but back to 1908. Back of 1908 food prices move somewhat irregularly as compared with general prices, but on the whole maintain an approximately even pace from 1897 to 1909.
The following table gives some interesting by-products of our study for the period 1896-1909.
We note from column (2) that deposits (
M‘) have grown, not only absolutely, but relatively to money (
M), changing, from a little over threefold to a little over fourfold the money in circulation. The figure for the panic year, 1907, was the highest but one, and
the drop in the succeeding year was the largest drop in the table.
Column (3) shows the “virtual” velocity of money, based on the idea that the total work of exchange, even that performed by checks, is really the work, indirectly, of money. It is simply the quotient of the total exchange work done, divided by the total money in circulation
and in banks.
| (1) | (2) |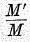
(3) VIRTUAL VELOCITY |
(4) |
(5) |
|---|---|---|---|---|
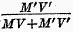| 1896 | 3.1 | 80 | .14 | .86 |
| 1897 | 3.2 | 84 | .14 | .86 |
| 1898 | 3.3 | 89 | .13 | .87 |
| 1899 | 3.8 | 103 | .12 | .88 |
| 1900 | 3.6 | 99 | .12 | .88 |
| 1901 | 4.2 | 114 | .11 | .89 |
| 1902 | 4.3 | 115 | .11 | .89 |
| 1903 | 4.1 | 113 | .11 | .89 |
| 1904 | 4.2 | 107 | .11 | .89 |
| 1905 | 4.5 | 125 | .10 | .90 |
| 1906 | 4.3 | 132 | .10 | .90 |
| 1907 | 4.4 | 129 | .10 | .90 |
| 1908 | 4.0 | 107 | .10 | .90 |
| 1909 | 4.1 | 124 | .09 | .91 |
| 1910 (see p. 492) | 4.4 | 134 | .08 | .92 |
| 1911 (see p. 492) | 4.7 | 131 | .08 | .92 |
| 1912 (see p. 492) | 4.8 | 144 | .08 | .92 |
We note that this virtual velocity of circulation of money, or its efficiency in providing for exchanges, has grown about 50 per cent. Its growth has been interrupted by occasional slumps, but all of these were trifling excepting that following the crisis of 1907.
The fourth and fifth columns give the solution of the much mooted question of the relative importance of check transactions (
M‘
V‘) and money transactions
(
MV),—a question to which many writers, including Professor Kinley, have given much attention. We find that in 1896 about 14 per cent of the business in the United States was performed by money and in 1909 about 9 per cent. In other words, checks performed in 1896 about 86 per cent of the total exchange work, and in 1909 about 91 per cent.
*33
These figures appear to afford the first fairly precise determination of the relative importance of check and money transactions. They confirm the belief
*34 that the relative part played by checks in the country’s transactions has substantially increased. The prevailing impression that they constitute nine tenths of all transactions is also seen to be correct.
e.g. Miss S. M. Hardy, “The Quantity of Money and Prices, 1860-1891. An Inductive Study.”
Journal of Political Economy, Vol. 3, pp. 145-168.
Quarterly Journal of Economics, February, 1908, p. 287.
op. cit., p. 149.
op. cit., p.114.
op. cit., pp. 110-111).
e.g. the remarks on these clearings in
Financial Review for 1910, p. 33, and in Babson’s
Business Barometers (Wellesley Hills, Mass.), 1910, p. 188.
Journal of the Royal Statistical Society on “A New Method of estimating the Velocity of Circulation of Money.” The additions incorporated in the Appendix (§§ 7, 8) include the statistical details of the calculations for the United States.
Quarterly Journal of Economics, 1907-1908, p. 287.
P will be much higher, if instead of taking the period beginning with 1879, which includes many years in which prices do not greatly change, we take the period beginning at the same time as my own figures begin, viz. 1896. The correlation coefficient for Kemmerer’s figures 1896-1908 is 83 per cent, which is far higher than that obtained by Persons for the period beginning in 1879.
M and
P the coefficient of correlation for 1896-1909 is 97 per cent.
relative deposits) is treated and represented by the letter
k.
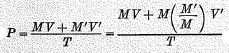,the statistics already obtained for 1909, and for that one factor remaining, the figure for 1896. This one factor remaining is, for the first hypothesis,
M; for the second,
M‘/
M; for the third,
V; the fourth,
V‘; and the fifth
T.
Bulletin of the United States Bureau of Labor show an uninterrupted rise in prices from January, 1909, to March, 1910. Between these dates the index numbers for wholesale prices rose from 124.0 to 133.8. For a good English-American comparison, see
Report of the (Mass.)
Commission on the Cost of Living. Boston, 1910, pp. 26, 56.
a reduction in the tariff would tend powerfully to reduce that level; for, as we have seen, a tariff wall acts like a dam in keeping up the high level accumulated by the original imposition of duties.
e.g. Cannon on Clearing Houses among the
Reports of the Monetary Commission, 1910.
Notes for Chapter XIII