The Purchasing Power of Money

APPENDIX TO CHAPTER XII

§ 1 (TO CHAPTER XII, § 1)
Professor Kemmerer's Calculations

Professor Kemmerer (Money and Prices, p. 99) estimates the money in circulation (M) by deducting from the money in the United States, as estimated by the Comptroller of the Currency, two items, viz. the money in the United States treasury and that in banks (reported and estimated). He then estimates the velocity of circulation of money as 47 times a year, and assumes, in the absence of any data by which to estimate its variations, that it remains constant. He arrives at the figure 47 as follows: The amount of check transactions he first estimates for 1896, at 143 billions (p. 111). This estimate is based on figures taken from Kinley's investigation, made through the Comptroller of the Currency in 1896. Referring to Kinley's estimate that check transactions are at least three times money transactions, he takes one third of 143 billions, or 47.7 billions, as the amount of money transactions. Estimating the amount of money in circulation at 1.025 billions for 1896, he divides 47.7 by 1.025 and obtains (p. 114) 47 times a year as the velocity of circulation of money. This figure, as we shall see, is probably nearly three times too large, the error arising from the fact that Professor Kemmerer does not accept the opinion expressed by Professor Kinley that his (Kinley's) estimate for the percentage of check circulation in 1896 was a "safe minimum," but expressed the contrary opinion that it was rather a safe maximum. We shall give reasons for believing that Kinley was quite right in concluding that the estimate of check transactions at three fourths of total transactions was a "safe minimum." The calculations which we shall presently offer prove nine tenths rather than three fourths to be the probable figure.

Professor Kemmerer, as already indicated, estimates check transactions (what we have called M'V') at 143 billions in 1896. For other years than 1896, there being no corresponding data, he estimates check transactions by assuming that bank clearings are always 35 per cent thereof (p. 118). He makes no attempt to estimate M' (bank deposits) and V' (their velocity) separately. The volume of trade (T) Professor Kemmerer estimates relatively (i.e. he estimates what we have called Q in the Appendix to Chapter X). This is confessedly one of the roughest parts of all his estimates. He seeks to get as many indicators as possible of the growth of trade (p. 130), without much regard to their suitability. His indicators are fifteen in number, viz. population, foreign tonnage entered and cleared, exports and imports of merchandise (values), revenues of Post Office Department, gross earnings from operation of railroads in the United States, freight carried by railroads, receipts of Western Union Telegraph Company, consumption of pig iron, bituminous coal, wheat, corn, cotton, wool, wines and liquors, and market value of reported sales on New York Stock Exchange. Representing each of these sets of figures by index numbers, he takes their simple average as the index number of trade for each year in question.

Of course, as Professor Kemmerer well realized, many of these figures are open to more or less serious objections. Population is a poor index of trade when trade per capita is changing. Values are inappropriate unless the prices are supposed constant, which cannot be the case for exports and imports, railroad earnings, or stocks, and can be only partially the case for post office revenues and telegraph receipts.

Having thus computed for 1879-1908 the various elements theoretically determining price levels (viz. MV + M'V' and T), Professor Kemmerer uses these to calculate an index number of prices. The index number thus calculated from the other magnitudes in the equation of exchange, he calls the "relative circulation." He then compares the figures for relative circulation (virtually from the formula P = (MV + M'V') ÷ T) with the actual statistics of price levels.

These directly calculated index numbers of prices he takes as an average of index numbers of wholesale prices (Common's figures and those of the Bureau of Labor, p. 137), wages (those of reports of Bureau of Labor, p. 137), and of the Industrial Commission), and prices of railroad stocks (Industrial Commission and Wall Street Journal), weighting them as follows: wages, 3 per cent; stocks, 8 per cent; wholesale commodities, 89 per cent.

The two sets of figures—"relative circulation" and "general prices"—presented visually by curves (p. 149), show a general agreement.

§ 2 (TO CHAPTER XII, § 2)
Method of Calculating M

The estimates for M, or money in circulation in the United States, are based on the reports of Comptroller of the Currency. The calculations are shown in the following table:—

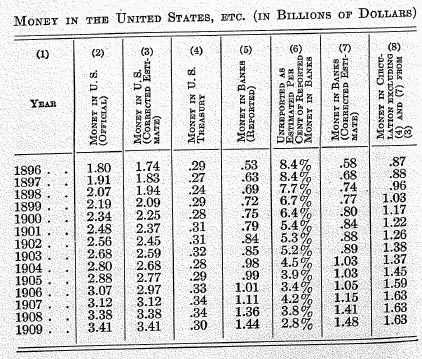
Column (2) gives the money in the United States in the middle of each calendar year according to the official estimates of the director of the mint. In 1907 these official estimates were corrected by subtracting an estimated error of $135,000,000 from the gold believed to be in the United States, this correction being made in view of the investigations of Maurice L. Muhleman. The mint corrections were made, however, only for the ends of calendar years.*36 In order to make the corrections apply to the middle of a given calendar year, the corrected figures for gold in the United States at the beginning and end of it were averaged. The average thus obtained was assumed to be the corrected figure for gold at the middle of the year. This corrected figure was then compared with the official figure for gold for the middle of the year and the difference assumed to be the correction for that date. This correction was then deducted from the figures for money in the United States given in column (2) above. We thus obtain the figures in column (3). Mr. Muhleman has made independent corrections for the middles of the years 1896-1900 inclusive. These are slightly smaller than those calculated from the mint figures as given above, the differences being in successive years, .05, .03, .00, .03, .05. Columns (4) and (5) of our table give the money in the federal treasury and the money reported in banks as stated in the annual reports of the Comptroller of the Currency. Column (6) gives the estimated percentage not reported. This estimate is found by assuming that the unreported reserves bear the same ratio to the reported reserves as unreported deposits bear to reported deposits, the latter ratios being calculated from the table given in the next section (§ 3) of this Appendix.

This estimated percentage being calculated and the correction found by it being added to the money in reporting banks, (column 5), we get the total estimated money in banks, (column 7). Column (8) is then found by subtracting from the corrected money in the United States (as given in column 3), the sum of the money in treasury (column 4), and estimated money in banks (column 7). These estimates of money in nonreporting banks are of course subject to some error; but even a 50 per cent error in the largest of them would not affect the last column much more than 2 per cent. A more important possible source of error is in column (2), which depends upon hypothetical estimates of gold in the United States. Mr. Muhleman writes me that in his opinion the corrections made by the Mint Bureau are not adequate. The corrections as made by that Bureau and here adopted affect several of the figures in column (8) by as much as 10 per cent. The errors in these corrections would presumably be much smaller than this. There are few other sources of error and, taking all things into account, it seems likely that the results are in general trustworthy—subject to a probable error of perhaps 2 or 3 per cent. This is fair accuracy as ordinary statistics go.

§ 3 (TO CHAPTER XII, § 2)
Method of Calculating M'

The calculations for obtaining M', or individual deposits subject to check, are shown in the table on page 49.

The figures of column (2) are those of "Individual Deposits" taken from the annual reports of the Comptroller of the Currency (see Report for 1909, pp. 64-66). For the years 1896-1899 correction is made for deposits of trust companies and savings banks misclassified as individual deposits. Prior to 1900 many banks included such deposits of bankers as individual deposits. They should be deducted because such deposits in one bank by other banks are not generally used for commercial purchases, but for banking operations. These deposits, to be deducted from column (2), are given in column (3).

The figures in column (3) are estimates based on the fact that the deposits of savings banks and trust companies in national banks are (whenever comparison is possible, viz. 1900-1908) found to be approximately equal to the deposits of state banks in national banks. As the state bank figures are available for 1896-1899, they are taken in lieu of the missing trust and savings figures. Since the original edition of this book was printed, consultation with the Comptroller has convinced the writer that these corrections are too large and that it would have been better to have omitted them altogether. They are retained, however, in order not to necessitate numerous changes in the plates. Fortunately, as will be seen on page 492, the net error thus retained is very small.

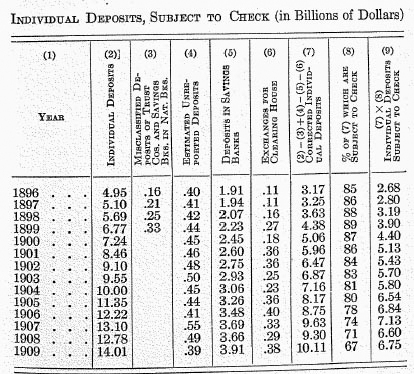
After deducting the correction of column (3), our next step is to add the correction of column (4), the estimated deposits unreported.

The figures for nonreporting banks for 1900 and 1902-1909 are the official estimates of the Comptroller of the Currency. (Those for 1900 and 1902 are entered in the Comptroller's tables under the rubric "reporting capital only" instead of "nonreporting," but I am assured by the Comptroller's office that this is a distinction without a difference.) The figure for 1901 is interpolated between those of 1900 and 1902. The figure for 1896 is estimated by the aid of two assumptions. The first assumption is that the unreported deposits in that year should be larger relatively to all deposits than was the case in 1903, as the table shows that the farther back we go the larger is the percentage of missing deposits. This consideration indicates that the correction exceeds .28. The second assumption is that the correction should be less absolutely than in later years; because the total deposits were then much less than later; and because the official figures in column (4), viz. those for 1900 and 1902-1909 show, as we proceed backward in time, that there is a slight tendency for them to grow less in absolute amount. (The chief exception is for 1909, when the special investigation of April 28 reached an unusual degree of accuracy.) This consideration would make the correction less than .50. Therefore, between .28 and .50 we select .40 as a rough mean. The error involved is not likely to affect the final column more than 3 or 4 per cent. The corrections for 1897-1899 are interpolated.

Column (5) gives a correction to be subtracted, viz. the deposits in savings banks. These deposits, by the nature of the case, are not used as a circulating medium, but are nevertheless included in the official "individual deposits" of column (2). The item for 1909 as here given includes, besides the reported figures, an additional item of .20 (i.e. $200,000,000), being the savings accounts of the state banks of Illinois. The inclusion of this Illinois item is simply in order to make the figures for 1909 comparable with those of the preceding years in which the same item had always been included (see Comptroller's Report, 1909, pp. 43-44).

Column (6) contains another, though small, subtractive correction, viz. the "exchanges for clearing house." In general, these exchanges represent checks which have been deposited by the persons receiving them but which have not yet reached the home bank and been charged against the persons who drew them. Any one (except a sharper or a blunderer) will, as soon as he has drawn a check, deduct the amount of it (say $100) from his deposit balance and refrain from drawing against it again. Such a person—say Smith—regards the $100 as transferred to his drawee—say Jones—and no more Smith's than money would be which he had paid out. But it takes time before the bank on which Smith draws knows of this transfer of Smith's deposits to Jones. In the meantime the bank books still include this $100 among Smith's deposits. The total figure for deposits is not disturbed by the inclusion of the $100 in Smith's account provided it is not included in Jones's account also. But when Jones deposits the check in his bank, this (Jones's) bank adds $100 to Jones's account before Smith's bank can deduct it from Smith's account. That is, the $100 is temporarily counted as both Smith's and Jones's. If both sides of this transfer were recorded at the same time, there would be no double counting. But until the check reaches Smith's bank the only record of the deduction which should be made from Smith's account is in the "exchanges for clearing house" which, accordingly, we must deduct in our statistics.

These figures, however, have to be estimated. Only for April 28, 1909, are they given for all banks, the figures being those of the special Report of the Monetary Commission already referred to. Of this amount, four fifths are of national banks; and as national banks report annually their exchanges against clearing houses, we assume that the total each year is five fourths of that reported by the national banks (see Comptroller's Report, 1908, pp. 514-522). The whole correction is so small that any error in this assumed ratio is quite negligible in the final result.

Column (7) is derived by applying to column (2) the above mentioned corrections,—deduction of items in column (3), addition of those of column (4), deduction of column (5), and deduction of column (6).

But even yet we have not reached the desired item,—deposit currency, or deposits subject to check. The net individual deposits which we have estimated include, not only current accounts, but deposits on certificate and other deposits which are considered investments rather than media of exchange. The first published attempt to give the true deposits subject to check is that of the National Monetary Commission. In their valuable special Report as of April 28,1909, constructed through the Comptroller of the Currency, the checkable deposits are given as 6.94 billions.*37 This 6.94 is subject to an addition for "nonreporting banks" and a deduction for "exchange against clearing house." The unreported deposits of all kinds are estimated for 1909 in the table at .39, of which, by proportion, only 6.94/14.01 of .39 or .19, is probably checkable. The .38 exchanges against clearing houses must be assumed to be almost wholly against deposits subject to check. The net corrected figure is therefore 6.94 + .19 - .38 or 6.75 billions as the checkable deposits in 1909. These constitute about 67 per cent of the "net individual deposits" of column (7).

This figure for checkable deposits in 1909 is found at the bottom of column (9) in the table. As it is only 67 per cent of the net individual deposits, and as it could not be assumed that the same ratio obtained for other years, I was unwilling to guess at the deposits subject to check for these other years without further light. Accordingly I wrote to Mr. A. Piatt Andrew, then Director of the Mint, and asked him whether, in his capacity as advisor to the Monetary Commission, he could not have a search made among the Comptroller's records for 1896 and a few other years in order to obtain the corresponding ratio for such years. Through his kindness and that of the Commission and Comptroller, in acceding to my request, it has been made possible to work out the corresponding ratio for 1896 as 85 per cent; for 1899 as 89 per cent; and for 1906 as 78 per cent.

Mr. Andrew gives 4.97 billions as the total (uncorrected) deposits of all banks as of July 14, 1896. This figure is slightly more complete than what I had already used from the Comptroller's Report (viz. 4.95), doubtless because, for this particular inquiry, a larger number of banks were included than had originally been used in the Comptroller's tables. Mr. Andrew gives the checkable deposits as 2.59 billions. This figure is subject to two corrections: one to account for unreporting banks, and one to account for exchanges for clearing house. We have estimated the deposits of nonreporting banks at .40; and, since Mr. Andrew has discovered in such banks .02 more total deposits (4.97) than the Comptroller reported, we must assume that there are .02 less unreported deposits in his figures than in the Comptroller's. This would make the estimated unreported deposits for Andrew's figures .38 instead of .40 which we assumed for the Comptroller's. The part of this ascribable to the deposits subject to check (2.59) is (2.59/4.97) × .38 or .20. This is the first (and additive) correction. The second (and subtractive) correction is the exchanges for clearing house, viz. .11. The final corrected figure is therefore 2.59 + .20 - .11 or 2.68. The ratio of this to the "net deposits" is 2.68/3.17 or 85 per cent.

For 1899, Andrew's figures for total net deposits are 4.38 and for checkable deposits 4.09. His figures for total deposits (7.07) are .30 completer than those of the Comptroller employed in the first column of the above table, and thus reduce the estimate for nonreporting banks applicable to Andrew's figures from .44 to .14, of which (4.09/7.07) × .14 or .08 are ascribable to the deposits subject to check. The correction consisting of exchanges for clearing house is .27. The figures for checkable deposits are therefore 4.09 + .08 - .27 or 3.90, which is 89 per cent of the "net deposits" (4.38).

For 1906 Andrew's figures for total net deposits are 8.75 and for checkable deposits, 6.90. His figures for total deposits (12.37) are less complete than those of the Comptroller, thus increasing the estimate for unreporting banks applicable to his figures from .41 to .61, of which (6.90/12.37) × .61 or .34 are ascribable to the deposits subject to check. The exchanges for clearing house were .40. The figures for checkable deposits are therefore 6.90 + .34 - .40 or 6.84, which is 78 per cent of the "net deposits" 8.75). We thus have figures for column (9) and column (8) for the years 1896, 1899, 1906, 1909.

If now, for intervening years, we interpolate evenly between these percentage figures for the years 1896, 1899, 1906, 1909, we shall have column (8) of the preceding table.

Column (9) may next be formed for the remaining years by applying the percentages in column (8) to the net individual deposits in column (7). Thus the table is made complete.

The results are of course subject to a probable error which, however, is believed to be only some 2 or 3 per cent for the years 1896, 1899, 1906, 1909, and perhaps double as much for years midway in the intervals between these four years.

It seems strange, since so much has been said of the relative importance of check and money circulation, that no attempt has previously been made to estimate or record the volume of the currency which circulates by check. This currency and its circulation are of many times the statistical importance of money and its circulation. Our wonder is the greater when we consider that "deposits subject to check" have been regularly reported by individual banks to the Comptroller of the Currency. The published figures began in the '60's to omit this category and lump all "individual deposits" together, and subsequent reports have simply followed the precedent thus established. The present Comptroller states that he intends, hereafter, to separate the item of deposits subject to check; so that we may hope from now on to have annual returns of the checkable deposits. We shall then know each year the magnitude of that item in our circulatory medium which, as we shall see, does nine tenths of the exchange work of the country.

§ 4 (TO CHAPTER XII, § 3)
Method of Calculating M'V' for 1896 and 1909

According to the Comptroller's Report for 1896, the total sum (money and checks) deposited in all reporting banks on the settling day nearest July 1, 1896, was 303 millions. Professor Kemmerer's allowance for nonreporting banks (op. cit., pp. 110-111) brings the figures up to 506 millions. The proportion of checks found in all deposits reported was 92.5 per cent, which, if applied to the estimated 506 millions of total deposits, will give 468 millions as the total checks deposited in one day. But July 1, being a first day of the month, would show exceptionally large deposits. In order to determine how much allowance to make for this fact, I have obtained, through the kindness of Mr. Gilpin of the New York clearing house, the figures for the New York clearings of July 2, 1896. July 2 was selected because the checks deposited in New York July 1 would appear in the clearing house statistics of July 2. The clearings for July 2 amounted to 157 millions, while the daily average for 1896 was only 95 millions or 60 per cent as much. Thus, the excessive clearings of July 2 have to be corrected by multiplying by .60 in order to reach a true average for the year. It is perhaps fair to assume that the deposits made on July 1 in New York require substantially the same correction. If we could assume that the abnormality of the day's deposits in the rest of the country were exactly like that of New York, requiring the same correction factor (.60), then this correction factor would apply to the whole country. But this assumption we cannot make. Doubtless .60 is too small an estimate of the true multiplier for the whole country outside of New York. The departure from the average was probably somewhat less than in New York City.

That this is the case appears likely for various reasons. In the first place New York is more sensitive to the variations in business activity than the country generally. Consistently with this view, we find that the percentage fluctuation in clearings from year to year is much greater in New York than in the rest of the country. By comparing each year with the next, we find this to be true of all except five of the twenty-seven years from 1883 to 1909*38 inclusive.

Again, the quarterly and semiannual dividends would cut a larger figure in a financial center like New York than in other places, in many of which few or no dividends are received.

Finally, in large cities like New York, checks are deposited more systematically and promptly, so that a fuller proportion of the first-of-the-month checks received on July 1 would be deposited on that day than in a smaller community. In the smaller community these checks straggle along to banks through several days after being received, thus tending to even up the daily flow and in particular to diminish the excess on and about July 1. We conclude that .60 is a minimum estimate for our multiplier for 1896.

Having obtained .60 as a minimum estimate, we next proceed to ascertain a maximum estimate. We may be reasonably sure that deposits outside of New York are so far subject to the influence of quarterly dividends, first-of-the-month payments, etc., that the volume of checks deposited outside of New York must to some extent exceed the average in 1896. We need to know to what extent we are safe in assuming that this outside volume of checks deposited on the day chosen exceeded the average. We can best reach such a safe estimate by means of some data on clearing houses in the Finance Report for 1896 (p. 493, Comptroller's Report). It is there shown that on July 1, or "the settling day nearest July 1," 66 out of the 78 clearing houses of the country had $228,000,000 of clearings. We are safe in assuming that the country's total clearings on that day were larger than this, because the returns as given include only 66 out of the 78 clearing houses of the country; and that on the following day they were larger still,*39 because it was then that occurred the bulk of the heavy July 1 deposits of checks. If the $228,000,000 clearings on July 1, 1896, were representative for each day of 1896, we could, simply by multiplying by the number of settling days of 1896, 305 days, find the total clearings of the country. But the result of this multiplication is 67.1 billions, whereas the actual clearings of the country for 1896 were only 51.2 billions. This is conclusive evidence that the clearings on July 1, and presumably still more those of July 2, exceeded the daily average and need to be reduced at least in the ratio 51.2/67.1 or .76.

Hence the true correction factor must lie between .60 and .76. Splitting the difference we have .68 as an estimate which cannot be far from the correct figures on either side; especially as .60 and .76 are so very safe or extreme limits. Figures very near either of them are improbable. The probable error is simply set at 5 or 6 per cent.

We turn now to similar calculations for 1909. At my request Professor Weston of the University of Illinois, through the kindness of Professor Kinley, has used substantially the same method for estimating the check circulation of 1909 based on Kinley's investigation*40 of that year for March 16. Professor Weston estimates the total check deposits of March 16, 1909, at 1.02 billions. This is below the daily average. A proof of this is found in the clearings of the New York clearing house on March 17, which reflect the deposits made in New York banks on the previous day; these were 268 millions, which was not representative of the year, as the average daily clearings were much greater, being 342 millions, or 28 per cent greater than those of March 17. 1.28 is therefore the correction multiplier we would apply if we could trust New York clearings to be a faithful barometer for the whole country. But since, as we have seen, New York is especially sensitive to speculative and other variations in banking operations, and as a part is usually more variable than the whole, it is reasonable to assume that the abnormality we find in New York of the deposits on March 16 exaggerates the abnormality of that day for the country at large, and that the correction multiplier should be less than 1.28. In order to set a safe lower limit, we may see what figure would result from the extreme assumption that outside of New York the day's deposits on March 16, 1909, were exactly the same as the daily average for the year. We can make a fairly good estimate of the resulting correction factor from the table on page 59.

This table is constructed from data taken from Kinley's report to the Monetary Commission on Credit Instruments (pp. 182, 186) together with the estimated corrections for the whole country's check deposits made by Professor Weston.

The figure for deposits in New York City is given for March 16, 1909. Deducting these figures from those estimated by Weston for the entire country, we have the deposits (786) outside New York. But the daily average in New York has been shown to be probably 28 per cent higher, or 306. These figures, added to those for deposits outside New York (786), give the daily average for the entire country, on the assumption that only New York City was abnormal on the day selected. The result (1092), compared with the actual deposits on the day selected (1025), shows the correction factor on the assumption that only New York was abnormal. This factor is 1.07. This furnishes a lower limit for the correction factor we are seeking.

CHECKS DEPOSITED (IN MILLIONS)
(1)	(2) NEW YORK CITY	(3) OUTSIDE NEW YORK CITY	(4) TOTAL U.S.
March 16, 1909	239	786	1025
Daily average if New York were alone abnormal	306	786	1092
Ratio average to actual = 1092/1025 = 1.07

Splitting the difference between our extreme limits, 1.07 and 1.28, we get, as our estimate of the correction factors, 1.17 in 1909 as compared with .68 for 1896. The range of possible error on either side is about 10 for 1909 and 8 for 1896. As the limits are all very extreme, the probable error must be much less—perhaps half as much. We may judge that the correction factors, .68 and 1.17, are probably correct within 5 or 6 per cent.

We conclude, then, that the 468 millions estimated as the actual check deposits made on July 1, 1896, must be multiplied by .68 in order to obtain the estimated average daily deposits in 1896. The result is 318 millions; which, multiplied by the 305 (settling days), gives 97.0 billions as our estimate for the check transactions in the United States for the year 1896.

Likewise, multiplying the estimated volume of actual check transactions in the United States on March 16, 1909 (viz. 1025 millions), by the correction factor, 1.17, we obtain 1.20 billions as the estimated daily average check deposits and transactions. Multiplying this by 303 (the number of clearing days of the New York clearing house and presumably the average number of banking days in the country), we obtain 364 billions as our estimate of the check transactions in the United States in 1909.

§ 5 (TO CHAPTER XII, § 3)
Method of Calculating M'V' for 1897-1908

Although New York clearings constitute two thirds of all clearings for the country, it cannot be imagined that the check transactions in and about New York form two thirds of the check transactions of the United States. We have already seen that the reported check deposits in New York on March 16, 1909, amounted to 239 millions. This figure, being for New York, is probably nearly complete and indicates, as we have seen, an estimated average for the daily deposits in New York City in 1909 of 306 millions. This gives 306 × 303 or 93 billions for New York City, for the entire year. Our estimate for the entire country was 364 billions, leaving 271 billions outside of New York City. Let us compare these estimated figures for checks deposited with the figures for clearings. The New York clearings in 1909 amounted to 104 billions and those outside New York, to 62 billions.

The New York clearings (104) thus exceed the New York check deposits (93), probably because the clearings on account of outside banks include clearings representing banking transactions as distinguished from commercial transactions, since New York City is the chief central reserve city. The New York City deposits were thus only 93/104 or about 90 per cent of the New York clearings. Outside of New York, on the other hand, the deposits far exceeded the clearings, being in the ratio 271/62 or 4.4. These ratios between check transactions and clearings, viz. .90 for New York and 4.4 for "outside," would indicate that the published figures for clearings should be weighted in the ratio of 4.4 to .9 or about 5 to 1. That is, on the basis of 1909 figures, five times the outside clearings plus once the New York clearings should be a good barometer of check transactions.

Of 1896, unfortunately, we lack the figures for New York City deposits. We have, however, figures for the deposits in New York state in both 1896 and 1909; and a study of these figures indicates that the ratio of weighting for 1896 should be something over 3 to 1. Not to put too fine a point upon it, we shall use the weighting 5 to 1 for all the years. The difference in the results between this system of 5 to 1 and a system of 3 to 1, or any intermediate system, will be small. but 5 to 1 is chosen because (1) the data for 1896 on which the number 3 is based are less certain than those for 1909, and (2) the New York clearings are not as good a representative of New York deposits as the outside clearings are of outside deposits; the New York clearings being somewhat vitiated by an element extraneous to New York and especially by the banking transactions connected with adjustments of bank reserves. We prefer, therefore, to give as much weight as possible to the "outside" clearings.

Having obtained our "barometer" of check transactions, viz. New York clearings plus five times outside clearings, we merely need to multiply this by the proper ratio in order to obtain the check transactions themselves. Absolute knowledge of this ratio of check transactions to the barometer exists only for 1896 and 1909, in which years we know the check transactions as well as the barometer. These ratios are .69 and .88. But we cannot err greatly in assuming that the intermediate years have intermediate ratios, varying regularly each year. The result is the following table:—

CLEARINGS AS BAROMETER OF CHECK TRANSACTIONS
(1) YEAR	(2) NEW YORK CLEARINGS	(3) OUTSIDE CLEARINGS	(4) BAROMETER (2) + 5 × (3)	(5) RATIO OF CHECK TRANSACTION TO BAROMETER	(6) M'V' CHECK TRANSACTIONS (4) × (5)	(7) V' VELOCITY OF CIRCU. OF DEPOSITS (V') (6) ÷ M'
1896	28.9	22.4	140.9	.69	97	36.2
1897	33.4	23.8	152.4	.70	106	37.9
1898	42.0	26.9	176.5	.72	127	39.8
1899	60.8	33.3	227.3	.73	166	42.6
1900	52.6	33.4	219.6	.75	165	37.5
1901	79.4	39.0	274.4	.76	208	40.6
1902	76.3	41.7	284.8	.78	222	40.9
1903	66.0	43.2	282.0	.79	223	39.1
1904	68.6	43.9	288.1	.81	233	40.2
1905	93.8	50.0	343.8	.82	282	43.1
1906	104.7	55.2	380.7	.84	320	46.8
1907	87.2	57.8	376.2	.85	320	44.9
1908	79.3	53.1	344.8	.87	300	45.5
1909	103.6	62.0	413.6	.88	364	53.9

As already indicated, only the first and last figures in column (5) are independently calculated, the rest being interpolated.

The other figures in the table explain themselves. The last column gives the very important magnitude which we have called the velocity of circulation of bank deposits subject to check, or the "activity" of checkable accounts. The probable errors of the last column are believed to range between about 5 and 10 per cent.

§ 6 (TO CHAPTER XII, § 4)
General Practical Formula for Calculating V

I. An Approximate Formula

For the purpose of tracing the circulation of money, and measuring it by bank records, we may classify the persons who use money in purchase of goods into three groups:—

1. Commercial depositors, i.e. all engaged in business—firms, companies, and others—who have bank deposits mainly or wholly apart from personal accounts.
2. All other depositors, chiefly private persons.
3. All who, like most wage earners, are not depositors at all. These three classes we shall distinguish as "Commercial depositors," "Other depositors," and "Nondepositors," or C, O, and N. The money in the possession of "Commercial depositors" we shall call "till money," and the rest "pocket money."

The three groups necessarily include all in the community who circulate money. By circulating money is meant expending it in exchange, not for some other circulating medium, as checks, but for goods.

The nature of these three groups of people must now occupy our attention. In countries advanced in the art of banking, "Commercial depositors" include practically all business establishments, and little else; "Other depositors" include most persons in the professional and salaried classes and proprietors, and little else; while the class of "Nondepositors" is almost coterminous with wage earners.

It is true that these characterizations of the three classes are not quite complete. "Commercial depositors," for instance, do not include some small business dealers, like street vendors, for these usually have no bank accounts. But the number of such is comparatively small in comparison with the number of business men or corporations who do have accounts, and, what is more to the point, the business they do is still smaller. It follows that the money they handle is negligible. In the United States, at least, excepting those rural parts of the South and a few other places where the money expenditures are very small, the custom of having bank accounts is practically universal among business men, firms, and corporations.

To keep a bank account is, in fact, a practical necessity of business. Without such an account a business man practically deprives himself of three of the most essential aids in modern business: the use of circulating credit; the use of remittance by mail; and the use of time credit.

Unless a dealer is obliged to pay "spot cash" or prefers to do so—and such cases are both few in number and insignificant in the amounts of money involved—he will almost invariably find it easier to make payment by check. Moreover, the very fact that most other business men use banking facilities creates in his mind the desire to have an account himself, both because he dislikes to appear "different," and because, when others pay him by checks, he finds it necessary to cash these checks,—a procedure which is always more trouble than to deposit them.

Cash payments are especially inconvenient when business is done at a distance. Remitting money by post, express, or personal delivery is troublesome, risky, and expensive as compared with posting a letter containing a check. Even a post-office money order is a clumsy and expensive substitute, and its use proclaims the user an insignificant financial factor.

Again, a business man without a bank account cannot usually obtain time credit, either from dealers or from banks. In the United States a bank likes to lend only to its own depositors. A business man who asks for a bank loan usually meets with the request to open an account. If he should seek a loan from another dealer, as for instance, his supply house, the absence of a bank account would arouse suspicions as to his business standing, and might lead to a refusal.

These facts, confirmed by observation and inquiry, have led to the belief that practically all business transactions in the United States, certainly over 99 per cent (measured, not by their number, but by their aggregate size), make some use of bank accounts. Even in localities where there are no banks, traders usually like to have a bank account in the nearest town, in order to facilitate their dealings as purchasers. We conclude, therefore, that the category of "Commercial depositors" coincides for all practical purposes with the category of business establishments.

"Other depositors" include most proprietors, professional, and salaried persons. Almost no wage earners are included, and almost no business establishments or business men in a business capacity. When a single individual conducts a business, he usually separates carefully his business self from his personal self. John Smith, the individual, and the John Smith Shop are distinct. The pocket money of the one and the till money of the other are not often confused. Where payments of money are made from one to the other, the transaction is regarded as of the same nature as the payments between the shop and any other person. Originally, and under primitive conditions, it is of course true that no such distinction was observed, and even to-day the differentiation is sometimes unmarked, e.g. in the case of hucksters, peddlers, fruit-stand dealers, and small country shopkeepers. But, as we have seen, these persons are not usually depositors anyway. Moreover, their number is small; and since by the nature of the case the money they handle is also small, their classification is, for practical purposes, a matter of indifference. It is true that occasional cases exist of ordinary business men who have the exclusive ownership of a business and do not take care to separate clearly their business and their personal accounts. Yet we may, in such cases, perform the separation in thought. When such a person withdraws money from his till and puts it in his pocket, we may say his business self has paid his personal self some dividends of the business. Likewise, his checks drawn are usually distinguishable as between his business or his personal expenses, even though he himself fails to keep two separate bank accounts. But such cases are rare and unimportant, because modern business of size is usually conducted by partnerships and corporations, where a strict separation of accounts is necessary to safeguard conflicting interests.

So much for the line of demarcation between "Other depositors" and "Commercial depositors." As to the line separating "Other depositors" and "Nondepositors," it should be observed that, although "Other depositors" include most proprietors and professional and salaried persons, yet some proprietors and professional men, especially in rural communities, and some salaried persons, chiefly small clerks, are "Nondepositors."

Finally, "Nondepositors" consist chiefly of those who are classed in statistics as wage earners. While there are some wage earners who are depositors,*41 they are rare; and while there are some "Nondepositors" who are not wage earners, especially (as just indicated) the agricultural proprietors (farmers) and small clerks, the amount of money circulated by them is small in comparison with the total circulation. While the line separating wages and salaries is not definitely marked in theory, it is usually easily recognized in practice.

Children under, say, twelve years need not be included in any of the three categories, as they are not handlers of money; at least, not to a sufficient degree to have any appreciable influence on the total circulation.

We may now picture concretely the main currents of the monetary flow, including the circulation of money in exchange for goods. Figure 18 illustrates the three principal types.

The corners of the triangle, C, O and N, represent the three groups of "Commercial depositors," "Other depositors," and "Nondepositors," and the B's represent banks. The arrows represent the flow of money from each of these four categories to the others. Thus B_o represents the annual withdrawals from banks by "Other depositors," O_c the spending of this withdrawn money by "Other depositors" among "Commercial depositors," and C_b the return of the money from the "Commercial depositors" to the banks. This circuit (B_oO_cC_b) of three links is very common. A second type of circuit is represented by a chain of four arrows (B_oO_cN_cC_b. It is illustrated by private depositors drawing money (B_o), and paying wages (O_n) to servants who in turn spend the money (N_c) among tradesmen who finally deposit it (C_b). A third type of circuit, also fourfold, is represented by the arrows B_cC_nN_cC_b. It is illustrated by commercial firms cashing their checks at banks (B_c) for pay rolls, with the cash so obtained paying wages (C_n) to workmen who spend it (N_c) among other tradesmen who redeposit it in banks (C_b). These three types are not the only ones, but they are so much more important than any others that they merit our undivided attention before a completer study is undertaken. Figure 18 has been constructed for the purpose of exhibiting them uncomplicated by other details.

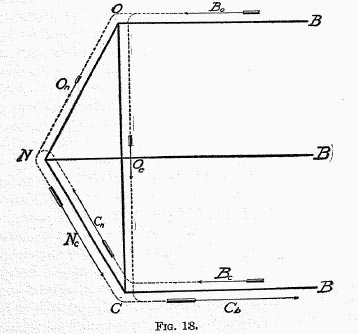
It will be noted that not all of the flows described are examples of the circulation of money. As already indicated, money may be said to circulate only when it passes in exchange for goods. Its entrance into and exit from banks is a flow, but not a circulation against goods. In the diagram the horizontal arrows represent such mere banking operations, not true circulation. On the other hand, the arrows along the sides of the triangle represent actual circulation. The diagram shows four such arrows, representing the four chief types of circulation: O_c payments of money from "Other depositors" to "Commercial depositors" in the purchase of goods; O_n payments from "Other depositors" to "Nondepositors," as when a housewife pays wages; C_n payments from "Commercial depositors" to "Nondepositors," as when a firm pays wages; and N_c payments from "Nondepositors" to "Commercial depositors," as when a wage earner buys goods of a merchant.

These four types of circulation of money occur in the three circuits already described, being sandwiched between the flows from and to the banks. The first, O_c, is contained within the circuit B_oO_cC_b, and since no "Nondepositors" intervene, represents money changing hands once between its withdrawal from bank and its re-deposit there. The remaining types (O_n,C_n, and N_c) are contained within the two other circuits (B_oO_nN_cC_b and B_cC_nN_cC_b), and, owing to the fact that "Nondepositors" intervene, represent money circulating twice between withdrawal and re-deposit.

In short, one of the three circuits (B_oO_cC_b) shows money circulating once out of bank. Both the others pass through N, and show money circulating twice out of bank. The diagram, then, represents all circulating money as springing from and returning to the banks; all of it as circulating at least once in the interim; and that portion handled by "Nondepositors" as circulating once in addition. Therefore, the total circulation exceeds the total flow from and to banks by the amount flowing through "Nondepositors." In other words, the total circulation in the diagram is simply the sum of the annual money flowing from and to banks and the money handled by "Nondepositors." The quotient of this sum divided by the amount of money in circulation will give approximately the velocity of circulation of money.

II. The Complete Formula

We have, however, still to consider the correction to be made for the less important forms of monetary circulation excluded from Figure 18.

In order to estimate the degree of accuracy of the first approximation just made for the circulation of money, we need to compare this approximation with a complete formula framed to include all possible transfers of money against goods.*42 There are nine possible kinds of transfers, three being respectively within each one of the three groups C, O, and N, and six being between each pair of these three, in either direction.

The exchanges possible within a class are (1) those between one "Commercial depositor" and another "Commercial depositor" (2) those between one "Other depositor" and another; and (3) those between one "Nondepositor" and another. The transfers possible between classes are (4 and 5) those between "Commercial depositors" and "Other depositors" in either direction; (6 and 7) those between " Other depositors" and "Nondepositors" in either direction; and (8 and 9) those between "Nondepositors" and "Commercial depositors" in either direction. Thus there are three interclass kinds and six interclass kinds of transfers of money against goods.

Figure 19 gives a complete picture of all these nine flows of money in exchange for goods; that is, of the entire "circulation of money." The nine flows are represented in the diagram by the nine arrows about the triangle, six being along the three sides of the triangle and representing interclass circulation, and three (c, o, and n) at the corners to represent interclass circulation. The remaining six arrows on the horizontal lines represent, of course, mere banking operations. The total circulation or monetary flow (F) in exchange for goods is, therefore, the sum of the magnitudes represented by these nine arrows, viz.

This is an exact formula for the circulation of money. We shall now compare it with the inexact first approximation, namely, "money deposited plus expenditures of 'Nondepositors.'" This comparison will express the error of the first approximation, and will suggest a method of transforming the exact formula (1) into a shape more suitable for statistical application. First, we need to express algebraically the first approximation. This may easily be done by inspecting Figure 19.

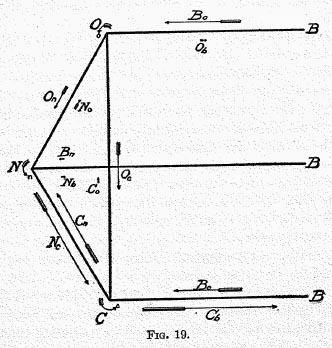
The total money deposited is C_b + O_b + N_b, while the total expenditure of "Nondepositors" is N_c + N_o. The sum of these two expressions we shall call F'. It is:—

which is, therefore, the algebraic expression for the first approximation.

To obtain the difference, F - F', between the exact and the approximate formula, we subtract (2) from (1), canceling N_c and N_o and placing the negative terms first. We thus obtain for a remainder (r) the following:—

That the value of F - F' is small may be seen clearly by transforming (3). We shall transform it by means of another equation (4) given below. In order to derive this new equation (4), we shall need to make a digression. This new equation is merely a special application of the general principle that the net outflow (i.e. outflow minus inflow) from the contents of any reservoir must equal the net decrease in its contents during the same time, or (algebraically expressed) that the net outflow (positive or negative) plus the net increase in contents (negative or positive) must be zero. We may apply this principle to any reservoir or store of money, but shall here find it most helpful to apply it to the reservoir of money contained among the "Commercial depositors" and "Nondepositors" taken together as one group. Let us designate the combination of these two as the "CN group." The total outflow indicated in the diagram from this "CN group" is evidently C_b + C_o + N_b + N_o, and the total inflow B_c + O_c + B_n + O_n. Hence, the net outflow, so far as the diagram shows us, is:—

This, plus the net outflow not shown in the diagram, is the true net outflow. Since the diagram was constructed to show only flows against goods (monetary circulation), and flows to or from banks, we have still to take account of money flowing in the community in exchange for something else than goods, and that flowing without any exchange at all, as well as any net outflow outside of the community.

We have thus to take account of three undiagramed flows. The first is the net outflow of money from the "CN group" to the "O group," which, though in exchange, is not in exchange for goods. This means simply cashed checks, for, according to the classification we are here using, "goods" are taken to include anything exchangeable, not either money or checks. Our first correction is, therefore, the net outflow of money from the "CN group" for cashing checks, i.e. the difference between the checks cashed by the "CN group" for the "O group" and those cashed in the opposite direction.

It will be understood that we have nothing to do here with the cashing of checks at banks, for this is included in the diagram (B_o, B_n, and B_c). Moreover, we have nothing to do here with cashing of checks within the "CN group," as when a storekeeper cashes a check presented by a "Nondepositor." We have only to do with the net outflow for cashed checks from CN to O. This net outflow (which may be positive, negative, or zero) we shall designate by the letter a, to stand for "accommodation" checks.

For the second correction, we have to designate the net outflow of money given away by the "CN group" in gifts, taxes, thefts, etc., for which no specific goods are received in return. This net outflow may be designated by g.

We have, thirdly and lastly, the net outflow of money with respect to the "CN group" outside of the community, i.e. the net amount of money which is lost to the country by export, fire, shipwreck, melting, etc., in excess of that imported, minted, etc. This net outflow may be designated by e, to stand for "external" outflow. Adding the net undiagramed outflow (a + g + e) to the net diagramed outflow, we have, for the total net outflow,

Now, on the reservoir principle already explained, the algebraic sum of this net outflow from the "CN group" and the net increase of the money in that group must be zero. That is, representing this net increase by i, we have

We now place this new equation (4) under the old equation (3), giving the value of r = F - F' in the following manner:—

Adding and canceling the terms of (3) and (4) indicated in parentheses, and rearranging the remaining terms, we have

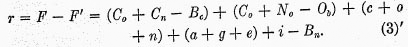
The letters are grouped in parentheses forming six terms, arranged, as far as can be judged, in the order of descending importance.

By using the expression just obtained for r, the complete formula (1) for the circulation of money may now be put in a form suitable for statistical application. Since r = F - F', then F = F' + r. Substituting for F' and r the expression already given in equations (2) and (3)', we have, as a transformation of (1),

= (1) all money deposited
+ (2) money expenditures of "Nondepositors"
+ (3) C's money expenditures from tills (i.e. money expenditures in excess of money withdrawn from bank)
+ (4) O's money receipts pocketed (i.e. money receipts in excess of money deposited in bank)
+ (5) intraclass monetary circulation
+ (6) CN's undiagramed net outflow of money
+ (7) CN's net increase of money on hand
- (8) N's withdrawals of money from bank.

This is a complete and universal formula for the circulation of money in any community. Its first two terms constitute the first approximation, and the other six terms constitute r, which may be called the "remainder term."

The first and second terms are by far the most important. The last three terms—sixth, seventh and eighth—are doubtless quite negligible under all circumstances actually met with. I am also reasonably confident that, in the United States, the 3d, 4th, and 5th terms amount to less than 10 per cent of the total and probably less than 5 per cent. Therefore, the complete omission of all except the first two terms would still give us a fairly good figure for the total F; for any one familiar with the inaccuracies of statistics knows that 5 or 10 per cent is a small error, especially for a magnitude which has hitherto eluded any attempt at measurement.

We may, therefore, distinguish three successive stages in our approximations. The first approximation comprises only the first two terms, viz. money deposited plus expenditures of "Nondepositors"; the second includes, in addition, terms (3), (4), and (5), viz. till-paid money expenditures of C, pocketed money receipts of O, and intraclass circulation; while the third is rendered absolutely complete by including terms (6), (7), and (8), none of which has practical importance. The complete formula is presented in the hope of arousing discussion and investigation which will disclose in particular to what extent it may be applied in countries where data exist for the first two terms, viz. money deposited and expenditures of "Nondepositors." The former is to a large extent a matter of daily record in most civilized countries, and the latter consists chiefly of wages, a magnitude which has for long been a favorite subject for statistical estimate.

§ 7 (TO CHAPTER XII, §4)
Application of Formula to Calculation of V for 1896 and 1909

We shall now exemplify the use of our formula by means of actual figures for the United States. The Report of the Comptroller of the Currency for 1896, already referred to, and the special report of the National Monetary Commission for 1909, give a basis for estimating the first term (C_b + O_b + N_b), the annual money deposited in banks in those years. Both reports were made under the direction of Professor David Kinley of the University of Illinois. We shall consider first the figures for 1896. The total money deposited in banks on the settling day nearest July 1, 1896, was 7.4 per cent of the total deposits of all kinds. This total for all reporting banks was 303 millions, of which 7.4 per cent would make $22,400,000. It was made up of over $16,200,000 from 3474 national banks, and the remainder from 2056 other banks. There were, all together, according to the Comptroller's Report, about 13,000 banks in the country at that time. On the basis of these figures, the Comptroller attempts to estimate the (retail) deposits of all kinds for all these 13,000 banks, assuming that the average deposit was the same as for the country banks replying. This average was $2375 for banks in places of 12,000 inhabitants or less. Applying this average to the unreporting banks, we would increase the retail deposits (which were $26,500,000) by an additional $17,800,000.

If we assume the same ratio of increase for the total money deposits, the sum of 22.4 millions would be increased by 15.0 millions, making a total of 37.4 millions, as the amount of money deposited in banks on the settling day nearest July 1, 1896. This figure represents at least a rough approximation to the inflow of cash into, and, therefore, also the outflow of cash from, the banks of the country. Multiplying by 305 settling days for the year, we obtain 11.4 billions as the total annual amounts deposited. The figures, being for the settling day nearest the first of July, are probably above the daily average for the year. Thus 11.4 is an upper limit rather than an estimate. Later we shall also set a lower limit.

The preceding figures relate to the year 1896. Similar calculations for 1909 have been made by Professor David Kinley *43 with the assistance of Professor Weston. The resulting figure for money deposited in 1909 is 19.1 billions.*44

But if it is necessary to adjust the figures for deposits of checks in 1896 and 1909 because the days selected are exceptional (see § 4 of this Appendix), it is also necessary to adjust the figures for the deposits of money. On July 1, 1896, many June bills must have been paid by cash as well as by check and on March 16, 1909, the middle of a month, there must have been slackness of settlements by cash as well as by check. Consequently, like the total deposits of checks, the total deposits of money made on July 1, 1896, were in all probability above the daily average for 1896, and on March 16, 1909, they were below the daily average for 1909. In other words, without adjustment for the abnormality of the days selected, the figure expressing monetary circulation for 1896 would be too large, and that for 1909, too small. That is, without such adjustment our calculations merely set an upper limit in 1896 and a lower limit in 1909.

But we may easily set the opposite limits. We may be reasonably sure that deviations from the average are less for money deposits than for check deposits. It cannot be expected that daily money deposits fluctuate as greatly as daily check deposits. Practically all check payments are influenced by the periodicity in receipts of checks by the depositors (as of their salary, interest, or dividend checks), or by the periodicity of credit extended to them (as of the tradesmen who render them monthly bills). While the fluctuations to which money payments are subject are more or less similar, they are much less in extent for two reasons: First, the payment or credit cycles which influence the fluctuations of money deposits are usually shorter than those which influence the fluctuations of check deposits; the wage earner usually gets his money weekly as against the salaried man who receives his check monthly, or the stockholder who receives his dividends quarterly. Secondly, unlike check payments, many, if not most, money payments have no payment or credit cycle. There is no credit cycle in what are called "cash" payments, for they imply that no credit is given. The receipts at "cash stores," the smaller receipts at all stores, the receipts of tramway, railway, and steamship offices, the receipts at theaters and many miscellaneous establishments are almost wholly on a cash basis and result in daily and fairly steady money deposits made by these establishments. These are facts of every-day experience and are confirmed by inquiry of bankers, who state that their money deposits are far steadier day by day than their check deposits. Confirmatory and conclusive evidence is also obtainable from Kinley's investigation in the Comptroller's Report for 1896 (p. 95). If check and money deposits were to fluctuate in perfect sympathy with each other, the percentage of the total which consists of checks would remain constant. But if, as we shall endeavor to show, the excess or abnormality of check deposits on July 1 is greater than the excess or abnormality of money deposits on that date, then we ought to find that the percentage of check deposits is greater on July 1 than usual. The figures of the Comptroller's Report indicate that this is the case. They show that the percentage of checks received (unfortunately not quite synonymous with "deposits") was on September 17, 1890, 91.0 per cent and on July 1 of the same year, 92.5 per cent, or 1½ per cent higher. Again, comparing July 1, 1896, with the nearest available date for another season of the year, namely, September 15, 1892, we find the figures to be as follows: for September 15, 1892, check receipts, 90.6 per cent; for July 1, 1896, check deposits, 92.5 per cent, or 1.9 per cent higher. The excess would have been still greater if both the figures were for receipts instead of one of them being for deposits; for, as the Comptroller says, the inclusion of other receipts than deposits tends to exaggerate the percentage of checks. That July 1 has a far larger proportion of checks than June 30 is indicated by the figures for retail deposits for June 30, 1894, and July 1, 1896, the former being 58.5 per cent and the latter 67.6 per cent, or 9.1 per cent higher. We should be cautious, however, in drawing any quantitative conclusion from this difference, since the investigations for 1894 and 1896 were conducted somewhat differently. But the difference, as we find it, harmonizes with all the facts at hand. Similar confirmation may be drawn from the absence of any contrast between the figures for June 30 and September 17, 1881, as compared with the sharp contrast already noted between July 1 and September 17, 1890. The credit receipts in 1881 on June 30 and September 17 were 91.77 per cent and 91.85 per cent, respectively, which figures are substantially equal, while, as above noted, for July 1 and September 17, 1890, we find a difference of 1½ per cent.

We feel, therefore, safe in concluding that check deposits are subject to greater fluctuations or abnormalities than money deposits. Consequently the deposits of money on July 1, 1896, while they may have exceeded the daily average, were probably not so far above the daily average as were the deposits of checks; also on March 16, 1909, the deposits of money were probably not so far below the average daily deposits of money as were the deposits of checks.

Now, if this were not true,—if the money deposits fluctuated exactly parallel with check deposits,—we should need to assume the same correction-factors for money as for checks, viz. .68 in 1896 and 1.17 in 1909, with the results given in column (1) of the following table:—

		ESTIMATED MONEY DEPOSITS OF YEAR
(1)	(2) MONEY DEPOSITED ON DAY SELECTED (IN MILLIONS)	(3) ASSUMING DAY AN AVERAGE ONE (IN BILLIONS)	(4) ASSUMING CORRECTION FACTORS EQUAL TO THOSE FOR CHECK DEPOSITS	(5) MEAN BETWEEN TWO PRECEDING COLUMNS
1896	37.4	11.4	7.8	9.6
1909	62.9	19.1	22.3	20.7

We see that the true value of the money deposited in banks in 1896 must in all probability lie between 7.8 and 11.4 billions, and in 1909, between 19.1 and 22.3 billions. If, in each case, we split the difference, the estimates become for 1896, 9.6, and for 1909, 20.7. The truth cannot be far from these figures, for there are only narrow limits on either side. The probable error, judged roughly from the calculated limits and from the character of the estimates of these limits, is placed at about 1 billion in each case. It will be noted, of course, that this error is larger proportionally in 1896 than in 1909.

We have now estimated the first term (total deposits) of the formula for the total circulation of money.

The next term (N_c + N_o) is the expenditure of the "Nondepositors" made to other classes. This is practically the expenditure of wage earners. The Census gives the average wages in manufacturing industries as $430. Mr. William C. Hunt of the Census Bureau, in an unofficial memorandum which he has kindly allowed me to see, has estimated that the laborers in the United States number about 18,400,000. Let us assume, as a reasonable approximation, that their average wages are the same as the average in manufacturing industries, namely, $430. We first apply this to the 8.5 millions of people which Mr. Hunt estimates are engaged in manufacturing and mechanical pursuits and trade and transportation. These persons, therefore, receive about 3.7 billions of dollars in wages.

The remaining classes of laborers are domestic servants and agricultural laborers. These, however, receive board and lodging as part pay. Since food and rent form about 60 percent of workingmen's budgets, we may assume that the actual money paid to domestic and agricultural workers is only about 40 per cent of that paid to manufacturing laborers, i.e. about $170. Mr. Hunt estimates the number of domestic and agricultural laborers at 9.9 millions. Hence the total money they handle in a year is probably about 1.7 billions. This, added to the previous 3.7 billions, gives 5.4 billions as the total money paid in wages in the United States All these figures relate to the year 1900, while the figures for our first term relate to 1896. In the interim both the number of laborers and their wages doubtless increased somewhat and we must, therefore, make a correction for each. We shall assume that the number of laborers increased in the same ratio as population, and that population increased between 1896 and 1900 at the same rate per annum as between 1890 and 1900. This would reduce the 5.4 billions to 5.0 billions. If, instead of population, we use the number of employees in manufacturing and mechanical pursuits as given by the Bureau of Labor,*45 the result is lower, viz. 4.6. The truth probably lies between, since agricultural labor, for which we have no statistics, has probably not increased as fast as manufacturing labor, and, therefore, even if labor as a whole increased in the same ratio as population, the relative increase of manufacturing labor, as compared with agricultural labor, would mean a greater payment of money wages. We may select 4.8 billions as close to the truth. As to the rate of wages, the index numbers of the Bureau of Labor*46 for 1896 and 1900 are 99.5 and 104.1 respectively. On this account, therefore, we should still further reduce our estimate of money wages paid in 1896,—in the ratio of 104.1 to 99.5 or from 4.8 billions to 4.6 billions. Furthermore, a small fraction of these laborers are prosperous enough to have bank accounts, and the expenditures of these should not be included among the expenditures of "Nondepositors." About 4½ billions is probably as close to the truth as we can expect to get.

But we must now add to this an allowance for "Nondepositors" other than wage earners. Some of the 2.1 million clerks and 8.6 million proprietors and professional men in Mr. Hunt's estimates, though not laborers, are nevertheless "Nondepositors." As to the clerks, it is said by business men that most clerks who receive over $100 a month, and some who receive less, have bank accounts. Probably, the great bulk of the 2 millions of persons estimated as clerks are far below $100 a month, and many are doubtless included who, like office boys, have less than what are ordinarily called wages. To make a guess sure to be large enough, let us say that three-fourths of the clerks have no bank account and average $60 a month. Even then the total cash-paid clerk hire would scarcely exceed a billion.

Among the proprietors and professional men, the only group we need to consider is agricultural proprietors (5.7 millions). The remainder consists of classes among which bank accounts are practically universal. Of these agricultural proprietors, those who have no bank accounts are doubtless smaller ones, living in districts where little money changes hands. Their number could certainly not exceed four millions, which would be over two thirds of the whole. The problem is, What cash do these farmers pay to depositors, commercial and other? Practically, this means, What do they pay to country storekeepers? Their payments to laborers or other farmers are payments to other "Nondepositors" and do not concern us here. For rent, food, or such farm supplies as they can raise themselves, they pay little or nothing. Thus, the hay crop of the nation is said to exceed in value the wheat crop; but so little hay is marketed that it is seldom quoted or thought of as a market commodity. Even the trade of these farmers with the storekeeper is conducted largely by barter or book credit. Their expenditures in actual money may be conjectured to average less than $250 a year for each farmer, making less than a billion dollars at most (even if the number of such farmers be counted at 4 millions).

It seems safe to say, then, after allowing a billion for clerks and a billion for farmers, that the total expenditures of "Nondepositors" cannot exceed 4½ + 1 + 1 = 6½ billions.

On the other hand, it can scarcely be less than 5 billions. To reduce it to this figure would require us practically to ignore the existence of "Nondepositors" other than wage earners, or to assume a large error in the estimate of wages.

We conclude that for 1896 the second term lies somewhere between 5 and 6½ billions. Placing it midway, we obtain approximately 5.7 billions with a possible error of .7 or. 8. Similar calculations for 1909 show 13.1 billions for the second term with a possible error of 1.0. To quote from Professor Kinley's article already referred to:*47—

"The second term of the formula is the money payments of 'Nondepositors,' made up principally, as Professor Fisher thinks, of the wages of working people. The following table shows an estimate of the increase from 1900 to 1909 in certain pursuits on the basis of the percentage of increase from 1890 to 1900 and on census and railroad returns since 1900. As far as possible salaried officers are eliminated.

	1890	1900	Increase Per Cent	Estimate 1909
Agricultural pursuits	8,565,926	10,381,765	21.2	12,362,605
Domestic and personal service	4,220,812	5,580,657	32.2	7,377,628
Total				19,740,233
Trade and transportation	1,977,491	2,617,479	35.2	4,275,913
Manufacturing and mechanism	4,251,613	5,208,406		6,935,113
Total				11,211,026

"A rough calculation based on the figures of Census Bulletin No. 93 gives us about $550 as the average yearly wages of people in manufacturing. If we should include mechanical pursuits, probably the average should be raised a little. Very likely $600 would be more nearly correct for this class.

"Again the Report of the Interstate Commerce Commission for 1907 gives figures from which it appears that the average yearly wage is about $640. It is more difficult to get a ground for making an estimate of the money wages of those engaged in agricultural and domestic pursuits. Doubtless it is more than, at first thought, might be believed. The money wages of domestic servants at present probably will average not less than $250 a year. Agricultural laborers are certainly receiving a good deal more than formerly, and $300 or $350 probably will not be too large a sum to assign to these. Accordingly, we may recapitulate as follows:—

Trade and transportation	4.3 millions at $640	$2,752 millions
Manufacturing and mechanical pursuits	6.9 millions at $550	$3,790 millions
Agricultural pursuits	12.4 millions at $300	$3,720 millions
Domestic and personal service	7.4 millions at $250	$1,850 millions
Clerks, etc., having no bank account		$1,000 millions
Total		13,112 millions

"This gives us the second term of the formula."

We have now estimated the first two terms (constituting together what has been called the first approximation) for both 1896 and 1909.

To this first approximation must be added the remainder, r, consisting of the many terms already explained, most of which are not known with exactness, but all of which are known to be small. The term "small" is always relative, and in this case a term is small for 1896 which is small compared to 16 billions. For instance, 160 millions is a mere trifle, being only 1 per cent of 16 billions, while 16 millions is only one tenth of 1 per cent. For purposes of comparison we do not need exact statistics for the various terms of which r is composed. All we need to know is that r is small and that it varies approximately as the rest of circulation varies. Under these circumstances a large mistake in estimating it will make a small error in comparisons. Only in case r were at once large and variable relatively to the other terms could a mistake in its estimation greatly affect the comparisons. Our attempt to estimate r has been made, not so much for the purpose of obtaining its absolute value, as to set for it wide and safe limits.

The magnitude r consists of all the five terms of our formula beyond the second. We shall take these up in order.

The third term of the formula is (C_o + C_n - B_c). This represents the till-paid commercial expenditures, or the excess of the money paid out by "Commercial depositors" over the money withdrawn by them from banks. Personal inquiry shows that the great bulk of the money withdrawn by "Commercial depositors" from the banks is drawn for the purpose of paying wages; also that the great bulk of the actual money expended by "Commercial depositors" is expended for wages. In other words, C_o is very small compared with C_n, and the sum of the two is nearly the same as B_c. Hence the difference (C_o + C_n - B_c), or till-paid expenses, is nearly zero. Till-paid expenses, being mostly wages and, as all observation shows, only a small part of total wages (4½ billions)—certainly not over one tenth—can be set down as less than half a billion in 1896 and less than a billion in 1909.

The fourth term (C_o + N_o - O_b) is O's money receipts which are pocketed instead of being deposited. Now O's money receipts, C_o + N_o, are small in the first place, for O, being depositors, usually receive their dividends, interest, and salaries by check. The chief exception is found in the rents and the professional fees paid by workingmen to landlords, physicians, etc., payments which constitute most of N_o. But these rents and fees paid by workingmen to private individuals are only a part of total rents and fees of workingmen, and the total rents and fees themselves are known by statistics of workingmen's budgets to be only about 20 per cent of wages. From this and other clews, we may safely set half a billion as an upper limit for the fourth term in 1896. Professor Kinley places .8 billion as the upper limit in 1909.

The fifth term (c + o + n) is the circulation within each of the three groups. Obviously only in trifling cases does money circulate between one "Commercial depositor" and another, between two "Other depositors," or between two "Nondepositors." Half a billion is put as an extreme upper limit for the total for 1896 and .8 by Professor Kinley for 1909. This would mean that about one dollar out of every thirty-five expended is passed on to other persons who are within the class to which the expender belongs. In fact, the universal testimony of such few representatives of c, o, and n as I have been able to interrogate personally is that the true ratio is less than this.

The remaining three terms are even more insignificant. In the normal state of equilibrium for the "CN group" it is evident that the sixth and seventh terms would both be substantially zero. The eighth term, withdrawals from banks by people who have no bank accounts, represents very exceptional conditions, such as where workmen cash checks at banks. Workmen seldom have checks to cash and, when they have, usually cash them in stores or saloons.

We shall summarize the estimates for each of the eight terms in the following table. Each term is placed midway between upper and lower limits estimated as safe, and the possible variation in either direction is indicated after a "±". Thus, $300,000,000 ± $300,000,000 means simply that, though $300,000,000 is assigned as the estimate, the true value may be more or less by an amount not exceeding $300,000,000, in other words, that the truth lies between $600,000,000 and zero. Instead of half billions we have used in the table $600,000,000 as being more easily divisible by two. The results for both years are given in the following table, in which generous estimates are given for the "probable error" in each case. In fact most of these "probable" errors are improbably large.

	1896	1909
1. Money deposited (Cb + Ob + N	9.6 ± 1.5	20.7 ± 1.5
2. Expenditure of "Nondepositors" (Nc + No)	5.7 ± .7	13.1 ± 1.0
3. C's expenditure, till paid (Co + Cn - Bc	0.3 ± .3	0.5 ± .5
4. O's receipts, pocketed (Co + No - Ob)	0.3 ± .3	0.4 ± .4
5. Intraclass circulation (c + o + n)	0.3 ± .3	0.4 ± .4
6. Net undiagramed outflow from CN (a + g + e)	0.0 ± .1	0.0 ± .2
7. Net increase of money of CN (i)	0.0 ± .1	0.0 ± .2
8. Money withdrawn from banks by "Nondepositors" (- Bn)	-0.001±.001	-0.001±.001
	16.2 ± 2	35.1 ±2

The first two terms (F') constitute the great bulk of the total. The remaining six terms (r) make up less than a billion more for either year. The total reaches about 16 billions as the estimated circulation of money in the United States in 1896. This estimate is subject to error, but not as much as the total of the possible errors of individual terms, which is over 3 billions. Even if each of the possible errors indicated were as likely as not to occur, the chance that in all eight cases they should all simultaneously occur in the same direction is (½)⁸, or one chance in 256. We may, therefore, "trust to luck" that the errors will, to some extent, offset each other. In fact, the chance of the error reaching the sum of those of the first three terms, or 3 billions, is less than a half. The "probable error" can therefore be placed with some confidence as less than 2 billions.

Dividing the figures we have obtained for the total circulation of money by the figures for the amount of money in circulation, we obtain figures for the velocity of circulation. These are 18.6 in 1896 and 21.5 in 1909, which show remarkably little change.

Reverting now to the remark with which we began the discussion of money velocity, namely, that it circulates but seldom outside of banks, let us picture our statistical results in the light of this fact.

Evidently, if all money circulated once only, then the bank record for 1896, showing about 9½ billions annually flowing into and out of the banks, would also exactly indicate the volume of the intervening work done. This would then be 9½ billions. But the true figure is, as we have shown, probably about 16 billions, and consequently we infer that some of the 9½ billions emanating from banks changes hands more than once before it returns.

Next let us suppose that all of the 9½ billions circulate once, except the part passing through the hands of "Nondepositors" (6 billions), and that the latter circulates twice. Then 3½ billions circulate once only. Under this assumption we can account for 3½ + 2 × 6 = 15½ billions of exchange work. But we have found in fact 16 billions. The difference of about half a billion is chiefly due to the existence of some money which circulates more than twice outside of banks.

The entire 16 billions may be roughly accounted for by dividing the 9½ billions flowing from banks into three streams; 3½ billions circulating once and once only; 5½ billions, twice and twice only; and ½ billion, three times. This makes 3½ + 2 × 5½ + 3 × ½ = 16 billions. Of the three parts, the first (3½ billions) is mainly the spending money drawn by "Other depositors," the second (5½ billions) is money withdrawn from bank for wages and other payments to "Nondepositors," and the third (½ billion) is the small amount not otherwise accounted for. This is only a rough scheme of division. A very small part circulates oftener than three times.*48

Similarly, for 1909, of the 21 billions flowing into and out of the banks, the 13 billions passing through the hands of "Nondepositors" must have circulated twice or more and thus have accounted for 26 billions or more of the total circulation (35 billions), leaving 21—13, or 8, to have circulated only once. This would account for 26 + 8 or 34 billions. The entire 35 billions may be accounted for by supposing the 21 billions flowing from banks to be divided into the following three streams:—

8 billions circulating once, making 8 billions,
12 billions circulating twice, making 24 billions,
1 billion circulating three times, making 3 billions.

The whole 21 billions, bank outflow, perform 35 billions of circulation before returning to bank.

The first two terms of the formula for the monetary circulation evidently give 15½ billions out of our estimated total of 16 billions for 1896, and 34 out of 35 for 1909; showing that the remainder, unless it has been greatly underestimated, is relatively small. The significance of this fact is that the terms most difficult to estimate statistically are least important. Of the two terms constituting the "first approximation," the first and most important is susceptible of the most accurate determination of all, while the second is made up chiefly of wages, which also are susceptible of statistical determination, or seem destined to become so.

In fact, if we should, as a statistical makeshift for the first approximation, merely add the amount of money annually withdrawn from bank to the annual money wages, we should, as to the year 1896, account for 9½ + 4½ or 14 out of 16 billions, leaving only 2 billions to be otherwise accounted for. In other words, this makeshift—the part most adapted to statistical measurement—accounts for about 88 per cent of the total circulation, leaving only 12 per cent for the part which can only be determined within wide limits. For 1909, deposits plus wages make up about 32 billions out of 35, or over 90 per cent. A still simpler makeshift is to add the deposits to the total wages without attempting to ascertain the part which is paid in money. This makeshift might be justified on the ground that total wages are more exactly ascertainable than the part paid in money, and that presumably the money part will maintain a fairly constant ratio to the total wages from year to year. The two parts here indicated may be distinguished as the measurable part (comprising the first term of our formula (1)' and most of the second term), and the conjectural part, comprising the remainder of the second term and the other six terms. Even if the allowance for the conjectural part should prove to be but half the truth, the measurable part would still constitute the great bulk of the total. The measurable part would therefore still be a safe practical index, or barometer of changes in the volume of circulation. Any excess of variation in the conjectural part, as compared with the measurable part, would, when spread over the whole, produce a disturbance only one fourth as great. It is reasonable to suppose that the conjectural and measurable parts will ordinarily vary together. If the measurable part varies 10 per cent, it is natural to suppose that the conjectural part, and therefore also the total of both, will vary likewise. But suppose this assumption erroneous and that, while the measurable part varies 10 per cent, the conjectural part really varies 14 per cent or 6 per cent. The difference between these and 10 per cent, i.e. 4 per cent, representing a supposed excess or deficiency of variation of the conjectural part, would produce a difference of only 1 per cent in the total! That is, the total, instead of varying 10 per cent, would vary 11 per cent or 9 per cent. Evidently, therefore, any unknown variation in the conjectural part can cause only a trifling variation in the result. In other words, the measurable part will always be a good index of the total—a reliable barometer of circulation. If we divide this by the quantity of money in circulation, we obtain a figure indicating the relative velocity of circulation of money from year to year. We conclude, therefore, that money deposits plus wages, divided by money in circulation, will always afford a good barometer of the velocity of circulation.

It is not always the absolute value of any magnitude we find most useful, but its relative value under different conditions. We may compare the relative length of two ships by measuring their water lines, although this method omits the overhang at either end. Such a comparison will apply roughly to any two vessels, and with great exactness to two ships of the same build. Similarly, our proposed barometer will afford rough comparisons for any two countries using banking facilities in comparable degrees, and will afford fairly exact comparisons for two successive years in the same country.

The proper statistical procedure would, therefore, seem to be to provide for the conjectural part by an estimated percentage correction, to be applied to the measurable part as a constant factor. Different correction factors will presumably apply in different countries, as, let us say, 10 per cent in the United States, 20 per cent in England, 30 per cent in France, etc. The chief value of such conjectural corrections would be to enable us to compare roughly the circulations and velocities of different countries. For comparisons in the same country at different times it would be almost immaterial what percentage correction were adopted or whether none at all were employed.

By means of the method which has been explained, it is believed that some interesting and valuable results can in the future be obtained, if statisticians in various lands will obtain (1) the total money deposited each year in banks (except by other banks), or, what is normally the same thing, the total money withdrawn from banks (except by other banks); (2) the total wages expended, or, what is practically the same thing, the total wages received; (3) if desired, a conjectural percentage addition to allow for the remaining and less known part of our formula; (4) the total money in circulation. The sum each year of (1) and (2) corrected by (3) and divided by (4) will be a very accurate barometer of the velocity relatively considered, as well as a fair approximation to its absolute value. The omission of (3) will not invalidate the results for purposes of relative comparison.

The importance of such accurate determinations can scarcely be overestimated, as the remarks on the subject by Jevons, Landry, and others have shown. When we know statistically the velocity of circulation of money, we are in a position to study inductively the "quantity theory" of money, and to discover the significance of that velocity in reference to crises, accumulation of wealth, density of population, rapid transit, and communication, as well as many other conditions. In fact a new realm in monetary statistics is laid open.

§ 8 (TO CHAPTER XII, § 4)
Interpolating Values of V for 1897-1908

To interpolate values for V we split the difference between two extreme hypotheses: the one of extreme steadiness; the other of extreme variability.

The first of these hypotheses is that V changes in a steady progression from its value of 18.6 in 1896 to its value of 21.5 in 1909. This would imply a perfectly steady growth with time, with no temporary fluctuations. But it seems unlikely that the velocity of circulation of money should not fluctuate somewhat from year to year. We have seen that, theoretically, there is a tendency under normal conditions for money expenditures (MV) to keep pace with check expenditures (M'V'). If this correspondence were perfect, we should have the ratio of MV to M'V', if not constant, at least changing in a perfectly even manner with time. Now this ratio for 1896 is 16.7 per cent and in 1909, 9.6 per cent. If we were to assume a perfectly steady change in this ratio during the intervening 13 years, the resulting value for V would have to vary considerably. This assumption is our second hypothesis of extreme variability. The following table shows the results of the two extreme hypotheses. It will be seen that in general there is no great difference between them.

YEAR	(1) HYPOTHESIS OF EXTREME STEADINESS	(2) HYPOTHESIS OF EXTREME VARIABILITY V VARYING AS NEEDED TO PRESERVE EVENLY CHANGING RATIO OF MV TO M'V'	(3) MEAN OF TWO PRECEDING
1896	18.6	18.6	18.6
1897	18.8	19.4	19.1
1898	19.0	20.6	19.8
1899	19.3	24.4	21.9
1900	19.5	20.4	20.0
1901	19.7	23.9	21.8
1902	19.9	23.6	21.8
1903	20.2	20.9	20.6
1904	20.4	20.9	20.7
1905	20.6	23.0	21.8
1906	20.8	22.5	21.7
1907	21.1	21.0	21.1
1908	21.3	18.6	20.0
1909	21.5	21.4	21.5

A supplementary calculation reveals the interesting fact that the "hypothesis of extreme variability" would make money velocity fluctuate approximately with deposit velocity. Splitting the difference between the two extreme hypotheses,—that of extreme steadiness and that of extreme variability,—we have what would seem to be an approximately correct estimate of actual velocity. It is probably correct in most cases for the first two digits. We cannot assume even for 1896 and 1909 that the third digit, that beyond the decimal, is correct, much less can we assume this to be true for the intervening years. But it is sometimes advisable to carry out the calculations to one digit beyond "the last significant figure."

§ 9 (TO CHAPTER XII, § 5)
Method of Calculating T

The table in the text is taken from the final column of the following more complete table:—

This table is constructed as follows:—

Column (2) is constructed for 1900-1909 from monthly figures on Internal Commerce published in the Monthly Summary of Commerce and Finance of the United States. By taking the monthly figures it was possible to obtain results for calendar years. This column is an average of separate indices for the following articles for which records were available. The original figures give the quantities of each article brought into the principal cities of the United States. These quantities were each multiplied by an assumed price which remained as a constant multiplier for every year. The products were then added together and the figures thus obtained taken to represent the total trade in these commodities, and to be a barometer of the relative internal commerce in the United States.

The articles referred to, and the dates for which data were used (as well as the price factors employed as explained below) are as follows:—

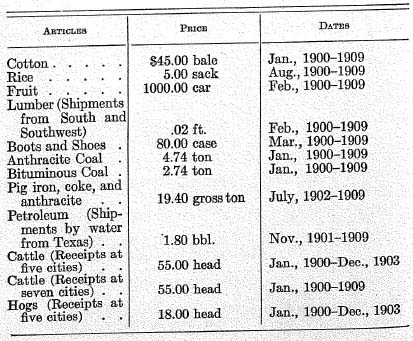
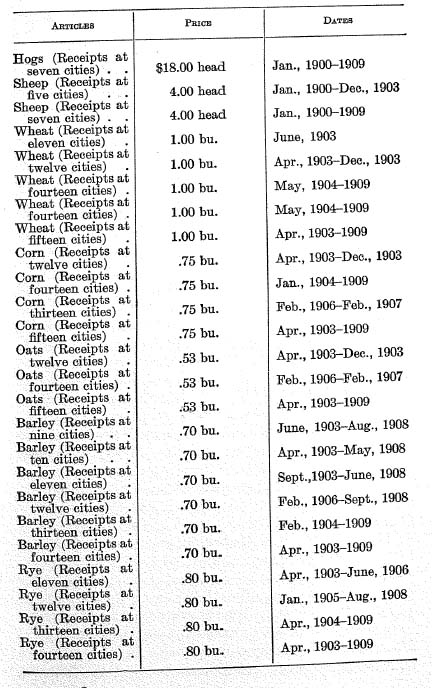
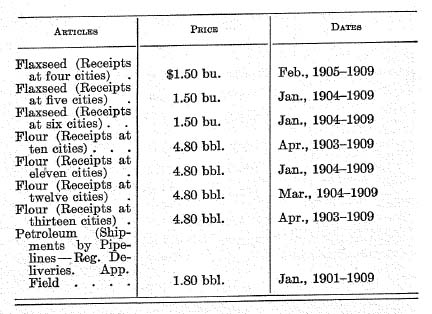
These articles are representative for the trade of the country and may well serve as a barometer of that trade. Yet the amount of trade, actually consisting of the sales of these articles in the few cities concerned, constitutes of course only a very small part (probably less than one tenth of 1 per cent) of the total trade of the country.

The actual figures first obtained were all divided by two before being entered in column (2) in order to bring them down to a scale more comparable with the figures of column (3). Since not all of the commodities were quoted in all the years, the table had to be "pieced out" for the defective years by the principles of proportion as already exemplified. As the statistics of the Monthly Summary go back only to 1900, the table had to be "pieced" back to 1896. This was done by using data from the statistical abstract of the United States and the abstract of the United States Census for 1900. The only figures obtainable for important articles in internal trade were those for grain, received during calendar years at fifteen principal primary markets, and for the estimated national consumption during fiscal years of the following articles, chiefly, or largely, of domestic production: cotton, wool, bituminous coal, pig iron, iron and steel railroad bars, and "distilled spirits, wines, and malt liquors."

The fiscal year figures were taken from 1896 to 1901 inclusive and reduced to calendar years on the assumption, for instance, that the true figure for the calendar year 1896 is the average of those for the two fiscal years ending June 30, 1896, and June 30, 1897. In this way we get hypothetical calendar year figures for 1896 to 1900. These figures and those for grains, which were already for calendar years, were then reduced by a factor so that each was made to be 111 for 1900, the number for that year found by the calculations involving the articles in the series, 1900-1909. The figures thus found were then averaged with weights selected to correspond with the estimates of their respective importance as judged from the estimates of their national consumption values and from the fact that some of them are indicators of large related businesses. The weights chosen were: for grains (including wheat, wheat flour, corn, rye, oats, barley, malt, and pease *49), 20; for bituminous coal, iron and steel, liquors, and cotton, 5 each; and for pig iron and wool, 1 each.

The data for 1896-1899 are far inferior to those for 1900-1909 taken from the Monthly Summary, and this for three reasons: (1) because they are so few in number; (2) because all except the grains are for fiscal years and the hypothetical correction to calendar years is subject to error; and (3) because all except the grains are very rough estimates of consumption, not based on shipments or receipts, but based on estimated production, corrected for exports and imports, which three elements are all subject to error.

We should not be surprised, therefore, to find larger errors in the resulting figures for 1896-1899 than for 1900-1909. In fact, we shall see that such is probably the case.

For carrying out the laborious operations involved in ascertaining the index numbers from 1900 to 1908, I am indebted to one of my undergraduate students, Mr. Robert N. Griswold, and for bringing them down to 1909, to one of my graduate students, Mr. W. Y. Smiley.

Column (3) is also based on laborious calculations which were performed by Mr. Griswold. The materials were also taken from the Monthly Summary of Finance and Commerce and covered 23 staple articles of import and 25 for export. The quantities of each were multiplied by a uniform price, and the sum of the resulting figures for imports and exports was taken. The articles of imports (with the price multipliers used) were:—

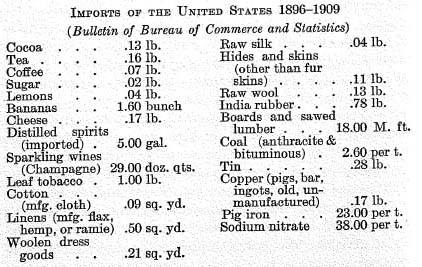
The articles of exports were:—

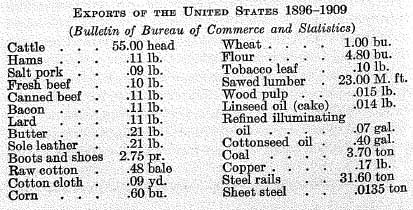
The statistics of exports and imports are probably fifty times as full as those of internal commerce and therefore (on the principle that probable errors vary inversely as the square root of the fullness of returns) some seven times as accurate. But, on the other hand, exports and imports represent less than 1 per cent as much trade as the internal commerce of the United States, and, by the principles already explained in previous chapters, should count in the equation of exchange only at half its value, one of the parties in the exchange being a foreigner. In spite, however, of the diminutive character of external commerce, it is to some extent an index of internal commerce; since a vast amount of internal business is a preliminary to exports and a sequel to imports, while perhaps a still larger amount is in other ways indirectly related to such commerce. By balancing these and other considerations, the relative weights to be assigned to the external and internal trade were selected as given in column (5).

Column (4) gives the sales of stocks according to the ordinary figures as given, for instance, in the Financial Review. These figures are, of course, not for values, but for amounts.

Column (6) gives the figures for tons of freight carried by railroads according to Poor's Railroad Manual for fiscal years.

Column (7) gives the figures for pieces of first-class mail matter carried in fiscal years. These figures were kindly supplied by the Post Office Department. They are lacking for 1896.

We have still to describe the method employed for combining columns (2), (3), (4), (6), (7).

The first three are regarded as constituting a group by themselves, representing direct indices of trade: and the last two are regarded as constituting another group of indirect indices.

The direct indices are combined by weighting the internal commerce, twenty, the exports and imports, three, and sales of stocks, one. These weights are, of course, merely matters of opinion, but, as is well known, wide differences in systems of weighting make only slight differences in the final averages.

In this way, column (5) is found.

As to the relative weights to be given to the railroad and post office statistics, the former were weighted as two and the latter as one. Railway tonnage represents almost every conceivable commodity in commerce and comes far closer to actual trade than post office letters.

After railroad and post office indexes are thus combined, the transition from fiscal to calendar years is made on the assumption that the figures for a calendar year are the mean of the figures for the fiscal years ending June 30 of that year and June 30 of the next year.

In this way column (9) is obtained.

From columns (5) and (9) column (10) is obtained by weighting (5) two, and (9) one.

Finally, column (11) is found by magnifying the figure of column (10) in the ratio 399/155 in order to make the figure for the base year, 1909, equal to 399 billions of dollars,—the total value of the left side of the equation (MV + M'V').

The probable errors in the values of T which have been calculated are believed to be some 5 to 10 per cent for the years 1900-1909 and 10 to 15 per cent for the years 1896-1900.

§ 10 (TO CHAPTER XII, § 5)
Method of Calculating P

The table in the text for index numbers of prices is taken from the last column of the table on page 487.

Column (2) gives the index numbers of the United States Labor Bureau (No. 81, March, 1909, p. 204).

I am under obligations to the Commissioner of Labor, Mr. Neill, for his courtesy in supplying me with the figure for 1909 in advance of publication.

Column (3) is taken from the Bulletin of the Bureau of Labor, July, 1908, p. 7.

Column (4) is from "The Prices of American Stocks, 1890-1909," by Wesley C. Mitchell, Journal of Political Economy, May, 1910. These figures are doubtless the best yet available in this difficult subject.

INDEX NUMBERS OF PRICES
(1) YEAR	(2) WHOLESALE, 258 COMMODITIES	(3) WAGES PER HOUR	(4) FORTY STOCKS	(5) WEIGHTED AVERAGE	(6) COLUMN (5) REDUCED TO BASIS OF 100 IN 1909
1896	90	100	77	89	63.3
1897	90	100	84	90	63.7
1898	93	100	94	93	66.2
1899	102	102	128	104	73.8
1900	111	105	134	113	80.2
1901	109	108	211	118	83.7
1902	113	112	250	125	88.7
1903	114	116	201	122	86.5
1904	113	117	192	120	85.1
1905	116	119	250	128	90.8
1906	123	124	267	136	96.5
1907	130	129	204	137	97.2
1908	123	-	201	130	92.2
1909	127	-	277	141	100.0

The general index number in column (5) is a weighted average of the figures in the three preceding columns, the weights being essentially the same as those used by Professor Kemmerer and for the same reasons.*50 For ease in computation the weights are taken in integers, viz. 30 for column (2), 1 for column (3) and 3 for column (4). This calculation brings the table down through 1907. As column (3) is defective for 1908-1909, these years and 1907 are worked out as averages of columns (2) and (4), the weights being the same as already mentioned. The result is two series of figures, one for all three columns ending in 1907, and the other for two columns beginning in 1907. As in this case it happens that both series have the same figure (137) for 1907, no corrections need be made in 1908 and 1909. The probable errors in the figures for P may be placed as about 5 to 10 per cent.

§ 11 (TO CHAPTER XII, § 7)
Mutual Adjustments of Calculated Values of M, M', V, V', P, T

There are various methods of calculating the best adjustments, involving the theory of least squares. But the problem may be greatly simplified by dividing the process into a few separate steps. First, we ascertain the best adjustments of the calculated values of each side of the equation of exchange considered as a whole. We shall need to exercise judgment in deciding the relative errancy of the two sides, but the total adjustments are so small that differences in judgment could not make much difference in the results.

After a careful weighing of all the evidence, it is believed that the errors in the right side (PT) are liable to be about double those in the left (MV + M'V'). Accordingly, the discrepancy between the two sides is corrected by changing PT twice as much as MV + M'V'; that is, by applying to PT a correction equal to two thirds of the total discrepancy, and by applying the remaining one third to MV + M'V', the two corrections being, of course, opposite and such as to bring the two sides into agreement. Thus, for 1899, the total discrepancy is 5 per cent, of which we assign about a third, say 2 per cent, to MV + M'V', and the remaining 3 per cent to PT. That is, we propose to increase the calculated figures for MV + M'V', by 2 per cent and decrease those of PT by 3 per cent. The result will bring them nearly into agreement at 185 billions. Sometimes the results will not exactly agree, as this method of adding and subtracting percentage corrections is only approximately correct; but any remaining slight discrepancies are readily adjusted by slight empirical changes in the factors. The result is shown in the Figure 20, which gives MV + M'V' and PT (reduced by dividing by 1.11) as originally calculated, and a mean (dotted) curve which is the revised estimate of both MV + M'V' and PT.

The corrections which are thus made in MV + M'V' and PT, by which they are brought into mutual agreement, are small; but the corrections necessary in the individual factors, M, V, M', V', P, T, are smaller still. We assume, for simplicity, that the percentage corrections to be made in M and M' are equal to each other and also that the corrections to be made in V and V' are equal to each other. This is a reasonable assumption; but even if some other assumption were made, the final results would be scarcely changed.

A correction of 1 per cent simultaneously in M and M' will produce a correction of 1 per cent in MV + M'V'. Likewise a correction of 1 per cent simultaneously in V and V' will produce a correction of 1 per cent in MV + M'V'. We may then regard the correction of MV + M'V' as practically consisting of two parts: one, the correction of M and M' and the other, the correction of V and V'. As the M's are more accurately ascertained than the V's, their correction should be smaller. Thus, for 1897, the total correction assigned to MV + M'V' is 3 per cent, of which we assign 1 per cent to M and M', and the remaining 2 per cent to V and V'. That is, we increase the calculated values of M and M' by 1 per cent and those of V and V' by 2 per cent, thus effecting (approximately) the desired increase of 3 per cent in MV + M'V'. In like manner the total correction assigned to PT is distributed over P and T, assigning the major part to T. By thus distributing the corrections over (1) M and M', (2) V and V', (3) P, and (4) T, we find that only very slight individual corrections are needed, the maximum being only 5 per cent and the vast majority (50 out of 56 cases) not exceeding 2 per cent. In fact, a decided majority (35 out of 56 cases) are within 1 per cent. It is really astonishing to think that a correction of only 2 per cent or less is usually required in our calculated values of M, M', V, V', P, T, in order to make them conform perfectly to the equation of exchange. In fact, 2 per cent is less than what might naturally be considered the probable error in most of the figures as calculated. This fact justifies confidence in the general correctness of our results.

Having thus corrected, by mutual adjustment, all the factors in the equation of exchange, we are left with a figure for P which is not 100 per cent for any one year. As we prefer to call 1909 the unit year, the figures for P are adjusted on that basis and the figures for T accordingly. This change disturbs the system of corrections as measured relatively to the original figures. It reduces to zero the correction of P for 1909. In general, it makes smaller the corrections for P and T for years near 1909 and makes correspondingly larger those for years remote from 1909. But, even so, the corrections never exceed 10 per cent for T nor 6 per cent for P. As the entire scheme of corrections thus outlined is a matter of judgment and each figure was frankly "doctored" on its own individual merits in view of all the circumstances in the case, it seems inadvisable to burden these pages by any fuller statement of the voluminous details of the process. The results as shown in Figures 13, 14, 15, and 16, already given in the text, speak for themselves.

§ 12 (TO CHAPTER XII, § 17)
Credit and Cash Transactions. Comparison with Kinley's Estimates

These figures agree surprisingly well with what might be expected from a rougher calculation from Kinley's investigations. For July 1, 1896, he found that money deposits constituted 7.4 per cent of all deposits and, on March 16, 1909, 5.9 per cent. Both of these figures are too low to represent the percentage of money transactions, for the reason that money often circulates more than once before being deposited, whereas checks in general circulate but once. The figure for 1896, especially, is too low, because of the excessive amounts of checks deposited on July 1. In fact, it was largely because the 1896 figures had been criticized in this respect that Kinley made the 1909 investigation. He did not, of course, take the figures of deposits as indicating exactly the ratios of check and money transactions. He recognized the fact that these would give too low a ratio for money and too high a ratio for checks. He expressed the belief that a safe minimum for check transactions in 1896 was 75 per cent*51 and in 1909, 88 per cent, implying that 25 per cent and 12 per cent were safe maxima for monetary circulation. Professor Kinley's purpose seems to be to establish safe maxima rather than to attempt exact estimates. Tabulating Kinley's figures, we have for money transactions expressed in percentage of all transactions:—

(1)	(2)	(3)	(4)	(5)
Year	Maximum (Kinley's estimate)	Minimum (as indicated by deposits)	Mean of two preceding	Present estimate
1896	25	7.4	16½	14
1909	12	5.9	9	9

According to this table, if we take the percentage of money in bank deposits as a lower limit of the percentage of money transactions, and if we take Kinley's estimates as a safe upper limit, and if we split the difference between these two limits, we shall reach almost*52 the same results as already reached by the more exact calculations in this book, which results are given, for comparison, in the last column. Thus the results of this book strikingly confirm those of Professor Kinley. They also agree remarkably well with the prevailing impression among business men that about 90 per cent of trade is now performed by means of checks.

ADDENDUM FOR SECOND EDITION

The figures in this second edition have been brought down to date by adding data for 1910,1911, and 1912 to the tables on pages 304 and 317 and inserting a new diagram between pages 306 and 307. (For full explanations as to these figures see page xxiii of this book and " 'The Equation of Exchange,' 1896-1910," American Economic Review, June, 1911; " 'The Equation of Exchange' for 1911 and Forecast," ibid., June, 1912; and " 'The Equation of Exchange' for 1912 and Forecast," ibid., June, 1913.)

Professor Wesley Clair Mitchell has kindly shown me the sheets of his forthcoming book (University of California Press) on Business Cycles, in which he has reëstimated the deposits subject to check (M') by somewhat different methods and with the aid of some data not available when the present book was written.

If I were rewriting this book, I should adopt Professor Mitchell's more perfect methods and results. But to do so now would involve a disturbance of a large number of plates for the sake of a very small net change in final results. I content myself, therefore, by here giving a table of Professor Mitchell's figures, including columns showing how much mine are larger or smaller.

PROFESSOR MITCHELL'S ESTIMATES OF DEPOSITS SUBJECT TO CHECK AND THE EXTENT TO WHICH THE PRESENT WRITER'S EXCEED OR FALL SHORT OF SAID ESTIMATES.
	MITCHELL'S RESULTS	F.'S EXCESS (OR DEFICIENCY)
		Unadjusted	Adjusted
1896	2.69	-.01	+.02
1897	2.75	+.05	+.11
1898	3.20	-.01	+.02
1899	3.87	+.03	+.01
1900	4.21	+.19	+.23
1901	4.96	+.17	+.17
1902	5.37	+.06	+.03
1903	5.54	+.16	+.19
1904	5.85	-.05	-.08
1905	6.56	-.02	-.02
1906	6.86	-.02	-.05
1907	7.11	+.02	+.02
1908	6.52	+.08	+.05
1909	6.81	-.06	-.13
1910	7.71	-.47	-.48
1911	8.24	-.46	-.46

APPENDIX TO THE SECOND EDITION, ON "STANDARDIZING THE DOLLAR"

THE plan for stabilizing the price level (and therefore the purchasing power of money) sketched in Chapter XIII (pages 340-346) in relation to the gold exchange standard has been more fully and more popularly explained since this book was written. (See, e.g., Report of International Congress Chambers of Commerce, September 26, 1912; Independent, January 2, 1913; New York Times, December 22, 1912; British Economic Journal, December, 1912. The most complete statement is that in The Quarterly Journal of Economics, February, 1913.)

The writer also hopes soon to publish a book devoted to this particular subject.

The following is an extract from an address in Boston before the American Economic Association, December, 1912, printed in the American Economic Review Supplement, March, 1913:—

Briefly stated, the plan is to introduce the multiple standard, in which the unit is a "composite ton" or "composite package" of many staple commodities, not of course by using such a package in any physical way but by employing instead its gold bullion equivalent. In essence it would simply vary the weight of gold in the dollar or rather behind the dollar. The aim is to compensate for losses in the purchasing power of each grain of gold by adding the necessary number of grains of gold to the dollar.

Both on the basis of theory and of facts, we may accept as sound the principle that the lighter the gold dollar the less its purchasing power and the more magnified the scale of prices; and that the heavier the dollar the greater its purchasing power and the more contracted the scale of prices. Evidently if we can find some way to increase the weight of the dollar just fast enough to compensate for the loss in the purchasing power of each grain of gold, we shall have a fully "compensated dollar," that is, a dollar which has constantly restored to it any purchasing power it may lose by gold depreciation.

We now have a dollar of fixed weight (25.8 grains), but varying purchasing power. Under the plan proposed, we should have a dollar of fixed purchasing power, but varying weight.

But how is it possible to have a dollar of varying weight without the annoyance of a constant recoinage of gold coin? Moreover, if this can be done, how can we know at any time what weight the dollar ought to have without leaving this to the tender mercies of some political official? Here are two very vital questions.

As a preparation for answering these two questions, it will be a little easier to explain the principle of the proposal if for a moment we assume that there are no actual gold coins in circulation, but only gold certificates. This supposition is, in fact, not very far from the truth in the United States; for, outside of California, there is very little actual gold coin in circulation. We have instead nearly a billion dollars of gold certificates in circulation, representing gold in the Treasury of the United States. We are supposing for the moment that gold circulates in no other way. Under these circumstances it is evident that the ultimate gold dollar is out of sight in the Treasury of the United States in bars of gold bullion. Every 25.8 grains of this gold bullion is a virtual dollar behind a dollar of gold certificates outstanding. A gold bar (of standard bullion) weighing 25,800 grains virtually contains 1000 gold dollars.

The gold miner takes such bars of standard gold to the mint and deposits them without waiting for their coinage, receiving gold certificates in return, one dollar of gold certificates for each 25.8 grains of standard gold which he deposits. On the other hand, holders of gold certificates may at any time receive gold bullion in return, when they desire this for export, or for use in the arts of jewelry, dentistry, gilding, etc., receiving 25.8 grains of gold for each dollar of gold certificates. Thus the government on demand gives or takes money at the rate of 25.8 grains of bullion per dollar; the virtual, though invisible, dollar being this 25.8 grains of gold bullion, nine-tenths fine.

The proposal here made is to change the weight of the dollar as an offset to changes in value. If there are no gold coins, it is very easy to do this. For example, if there should be a decrease of 1 per cent in the value, that is, purchasing power of gold, then the weight of gold bullion which constitutes the virtual dollar would be declared 1 per cent greater, becoming 26.058 instead of 25.8. If there should be an increase in the purchasing power of gold, the weight of the virtual dollar would be reduced accordingly. Whenever the gold miner took gold to the mint, he would receive a gold certificate not necessarily at the rate of one dollar for each 25.8 grains of standard gold, but for a larger or smaller amount as the case might be, the amount always being that amount which would possess the same purchasing power. Similarly the holder of gold certificates who wishes them redeemed in bullion for export or for the arts, would not always get exactly 25.8 grains for each dollar of certificates, but a larger or smaller sum, as the case might be. Thus the government would be receiving gold from the miner and giving it out to the jeweler just as at present, but in varying weights per dollar, instead of at the arbitrarily fixed weight of 25.8 grains. The weight of gold per dollar in which, at any particular time, gold certificates were redeemable would constitute the virtual and only gold dollar. Under these circumstances it is clear that it would be entirely feasible to change up and down the weight of the gold dollar (that is, the amount of gold bullion interconvertible with a dollar of gold certificates), and without any recoinage or other interference with the outward appearance of the currency in our pockets.

We should familiarize ourselves with another way of stating all this. Instead of saying that the government receives gold bullion at the mint and uses this for redeeming gold certificates, we may, if we prefer, say that the government buys and sells gold. It buys gold from the miner, paying for it in gold certificates; it sells gold to the jeweler, who redeems these certificates. At present, the price at which gold is bought and sold by the government is $18.60 an ounce (for standard gold nine-tenths fine). This is easily figured out from the weight of the gold dollar; for 25.8 grains of gold being our present dollar, each ounce (or 480 grains) of gold bullion contains 480/25.8 or 18.60 virtual dollars. To say, then, that we now have a fixed weight in our gold dollar, 25.8 grains, is the same thing as to say that we have a fixed government price for gold, $18.60 per ounce. To raise the weight of the gold dollar 1 per cent, or from 25.8 grains to 26.058 grains, is the same thing as to lower the government price of gold from $18.60 to $18.42 per ounce.

We come now to the second question: How would it be possible to know the proper adjustments to be made in the weight of the virtual dollar—the gold bullion inter convertible with each dollar of gold certificates—without putting a dangerous power of discretion in the hands of government officials? In other words, how can the adjustment in the weight of the virtual dollar be made automatic? The answer is: By means of statistics called "index numbers of prices." Such statistics are to-day published by the London Economist, the United States Bureau of Labor, the Canadian Department of Labour, and several commercial agencies, such as Bradstreet. The index number of the Bureau of Labor is based on the wholesale prices of 257 commodities, and shows from year to year the extent to which prices on the whole advance or fall,—the average movement of all the 257 prices.

There are various systems of index numbers, but they practically all agree remarkably well with each other. When once a system of index numbers is decided upon, their numerical calculation becomes a purely clerical matter. A statistical bureau (as for instance the present Bureau of Labor or an international statistical office) would compile and publish these statistics periodically and the actual prices on which they were based. If at any time the official index number showed that the price level had risen 1 per cent above par, this would be the signal for an increase of 1 per cent in the virtual dollar.

The plan, then, is: first, to provide for the calculation of an official index number of prices; second, to adjust correspondingly the official weight of the virtual dollar at which the government shall issue gold certificates to miners or redeem them for jewelers, in other words, to adjust the official prices of gold at which the government stands ready to buy or sell at the option of the public.

This, then, is the plan in brief—a plan virtually to mark up or down the weight of the dollar (that is, to mark down or up the price of gold bullion) in exact proportion to the deviations above or below par of the index number of prices.

A few additional details essential to the working of the plan may now be briefly mentioned. You are still waiting to see how actual gold coin could be used in such a system. To be continually recoining the gold in circulation would, of course, be quite impracticable. But this would be unnecessary. Existing gold coin would remain unchanged at 25.8 grains per dollar, and new gold coins would be given the same weight. Gold coins would simply become what silver dollars now are, token coins. Or, better, they would be, like the gold certificates, mere warehouse receipts, or, as it were, "brass checks" for gold bullion on deposit in the Treasury. Otherwise expressed, gold coins would be merely gold certificates printed on gold instead of on paper. They would be used exactly as gold certificates are used—namely, issuable to the gold miner in return for his bullion, and redeemable for those who wished bullion for export or in the arts.

The excess of bullion over the weight of the coined dollar itself would be analogous to what has generally been called "seigniorage"; so that in a sense, the plan may be described as a plan to restore the ancient custom of seigniorage on gold coin. Thus, if the virtual dollar were at any time 35.8 grains, the excess of ten grains above the weight of the coin dollar, 25.8 grains, would be "seigniorage." The gold miner, in return for every 35.8 grains of standard gold bullion taken to the mint, would receive, at his option, a gold certificate on paper, or a gold certificate on gold (that is, a dollar gold coin)—the latter containing, just as at present, 25.8 grains. Any holder of gold coin, old or new, and any holder of gold certificates could receive from the government gold bullion at the official rate declared from time to time. He would thus be receiving a larger quantity of gold bullion than the amount of bullion in the gold dollar. The gold coin would then, like all our other coins, be worth more as coin than as bullion, and its value would be determined just as the value of a gold certificate or any other paper money is to-day determined, by the ultimate bullion with which it would be interconvertible, this bullion being of greater weight than the weight of the dollar itself.

The only real complication which would be introduced by allowing gold coin to remain at its present weight and fineness would be to limit the operation of the system when prices tended to fall below the par or starting point at which the system began. The weight of the virtual gold dollar could never be reduced below the weight of the coin dollar; for, if this were done, the seigniorage would become a minus quantity and all the gold coin would be immediately melted into bullion, being worth more melted than coined. One proviso, therefore, in the system would be that the weight of the virtual dollar should never be less than 25.8 grains and that therefore the government price of gold should never be more than $18.60 per ounce. Perhaps, in view of the present dissatisfaction with high prices, many people would not object to this limitation which permits prices to fall below the present level, but does not permit them to rise further. Yet it is a poor rule that will not work both ways. Consequently, while I personally look forward to an upward tendency of prices in the future, the possibility of a downward movement should be provided for. For this purpose, gold coin could, if desired, be recalled at the outset and recoined in lighter weight, just as the Philippine peso was recalled and reduced in weight when the recent rise in the price of silver threatened to lead to melting the silver pesos. But I do not advocate crossing the bridge until we come to it. It would be sufficient to provide in advance for crossing it in case we should ever come to it. This could be done in one of two ways. It could be provided that, if ever the price level should, in the future, sink more than, say 10 per cent below the original par or price level from which the system started, all gold coins should then be withdrawn from circulation and gold certificates employed instead. In this way we should be rid of any complication from the use of gold coin, and would be at liberty forever after to adjust the weight of the virtual dollar downward as well as upward. Or, if preferred, it could be arranged that when prices should sink more than the suggested limit of 10 per cent below the original level, we should then recoin and reduce our gold coins. This would merely mean that the gold on which we print our gold certificates would be reduced in weight. It would not, of course, reduce the value of the gold coin any more than the reduction in the weight of the Philippine peso which was made for a similar contingency—or, to take an example nearer home, the reduction of 10 per cent in the weight of our subsidiary silver coins half a century ago—had any tendency to reduce the value of these coins.

If the latter plan were chosen, the amount of reduction in the gold coin should be enough to provide a comfortable margin for any similar emergencies in the future. Any subsequent recoinages would thus be deferred a long time and similar provision for them could be made. Personally I should prefer the former method, eliminating gold coins altogether.

Another essential detail is a proviso to avoid speculation in gold disastrous to the government. This would be accomplished by means of a slight government charge, say 1 per cent, for minting. This charge, which existed in former days, is called brassage. It would mean that the price at any particular date at which the government bought gold would be slightly less than the price at which it sold it. Without such a margin to protect the government, it is evident that when the government raised its price, say from $18 to $18.10 an ounce, speculators might, in anticipation of this rise, buy all the gold in the government vaults at $18 in order to sell it back to the government immediately after the change in price, at $18.10, thus profiting ten cents per ounce at the expense of the government.

Similarly, a fall in price, say from $18.10 to $18 per ounce, would encourage the opposite form of speculation. Holders of bullion would then rush it to the government to sell it at the present rate of $18.10, and immediately after the change in price, buy it back at $18, thus profiting again ten cents per ounce at the expense of the government. If, however, the government were protected by a brassage charge of 1 per cent and if it were provided that no single shift in the government pair of prices, whether they were both moved up or both moved down, should exceed the "brassage" or margin between them, it is clear that no such speculation could occur, for there would be a greater loss from the payments of brassage to the government than any speculative gain possible from the change in price.

Other details relate to the provisions for establishing and maintaining a gold reserve at the outset where no such reserve existed in the first place. In the United States we could utilize the 50,000,000 ounces of gold already in the Treasury for the very purpose of redeeming the $900,000,000 of gold certificates outstanding.

We have standardized every other unit in commerce except the most important and universal unit of all, the unit of purchasing power. What business man would consent for a moment to make a contract in terms of yards of cloth or tons of coal, and leave the size of the yard or the ton to chance? Once the yard was the girth of a man. In order to make it constant, we have standardized it. We have standardized even our new units of electricity, the ohm, the kilowatt, the ampere, and the volt. But the dollar is still left to the chances of gold mining. At first we could not standardize units of electricity because we had no adequate instruments for measuring those elusive magnitudes. But as soon as such measuring devices were invented, these units were standardized. We have hitherto had a similar excuse for not standardizing the dollar as a unit of purchasing power, and so a standard for deferred payments; we had no instrument for measuring it or device for putting the results in practice. With the development of index numbers, however, and the device of adjusting the seigniorage according to those index numbers, we now have at hand all the materials for scientifically standardizing the dollar and for realizing the long-coveted ideal of a "multiple standard" of value. In this way it is within the power of society, when it chooses, to create a standard monetary yardstick, a stable dollar.