The Theory of Political Economy
By William Stanley Jevons
THE contents of the following pages can hardly meet with ready acceptance among those who regard the Science of Political Economy as having already acquired a nearly perfect form. I believe it is generally supposed that Adam Smith laid the foundations of this science; that Malthus, Anderson, and Senior added important doctrines; that Ricardo systematised the whole; and, finally, that Mr. J. S. Mill filled in the details and completely expounded this branch of knowledge. Mr. Mill appears to have had a similar notion; for he distinctly asserts that there was nothing; in the Laws of Value which remained for himself or any future writer to clear up. Doubtless it is difficult to help feeling that opinions adopted and confirmed by such eminent men have much weight of probability in their favour. Yet, in the other sciences this weight of authority has not been allowed to restrict the free examination of new opinions and theories; and it has often been ultimately proved that authority was on the wrong side.There are many portions of Economical doctrine which appear to me as scientific in form as they are consonant with facts. I would especially mention the Theories of Population and Rent, the latter a theory of a distinctly mathematical character, which seems to give a clue to the correct mode of treating the whole science. Had Mr. Mill contented himself with asserting the unquestionable truth of the Laws of Supply and Demand, I should have agreed with him. As founded upon facts, those laws cannot be shaken by any theory; but it does not therefore follow, that our conception of Value is perfect and final. Other generally accepted doctrines have always appeared to me purely delusive, especially the so-called Wage Fund Theory. This theory pretends to give a solution of the main problem of the science—to determine the wages of labour; yet, on close examination, its conclusion is found to be a mere truism, namely, that the average rate of wages is found by dividing the whole amount appropriated to the payment of wages by the number of those between whom it is divided. Some other supposed conclusions of the science are of a less harmless character, as, for instance, those regarding the advantage of exchange (see the section on “The Gain by Exchange,” p. 141). [From the Preface to the First Edition]
First Pub. Date
1871
Publisher
London: Macmillan and Co.
Pub. Date
1888
Comments
3rd edition. Includes Preface by Harriet Jevons.
Copyright
The text of this edition is in the public domain. Picture of William Stanley Jevons: Photogravure after a photograph of W. Stanley Jevons, taken by Maull & Co., London., courtesy Liberty Fund, Inc.
Importance of Exchange in Economics.
CHAPTER IV
THEORY OF EXCHANGE
EXCHANGE is so important a process in the maximising of utility and the saving of labour, that some economists have regarded their science as treating of this operation alone. Utility arises from commodities being brought in suitable quantities and at the proper times into the possession of persons needing them; and it is by exchange, more than any other means, that this is effected. Trade is not indeed the only method of economising: a single individual may gain in utility by a proper consumption of the stock in his possession. The best employment of labour and capital by a single person is also a question disconnected from that of exchange, and which must yet be treated in the science. But, with these exceptions, I am perfectly willing to agree with the high importance attributed to exchange.
It is impossible to have a correct idea of the science of Economics without a perfect comprehension
of the Theory of Exchange; and I find it both possible and desirable to consider this subject before introducing any notions concerning labour or the production of commodities. In these words of J. S. Mill I thoroughly concur: “Almost every speculation respecting the economical interests of a society thus constituted, implies some theory of Value: the smallest error on that subject infects with corresponding error all our other conclusions; and anything vague or misty in our conception of it creates confusion and uncertainty in everything else.” But when he proceeds to say, “Happily, there is nothing in the laws of Value which remains for the present or any future writer to clear up; the theory of the subject is complete”
*65—he utters that which it would be rash to say of any of the sciences.
Ambiguity of the term Value.
I must, in the first place, point out the thoroughly ambiguous and unscientific character of the term
value. Adam Smith noticed the extreme difference of meaning between
value in use and
value in exchange; and it is usual for writers on Economics to caution their readers against the confusion of thought to which they are liable. But I do not believe that either writers or readers can avoid the confusion so long as they use the word. In spite of the most acute feeling of the danger, I often detect myself
using the word improperly; nor do I think that the best authors escape the danger.
Let us turn to Mill’s definition of Exchange Value,
*66 and we see at once the misleading power of the term. He tells us—”Value is a relative term. The value of a thing means the quantity of some other thing, or of things in general, which it exchanges for.” Now, if there is any fact certain about exchange value, it is, that it means not an object at all, but a circumstance of an object. Value implies, in fact, a relation; but if so, it cannot possibly be
some other thing. A student of Economics has no hope of ever being clear and correct in his ideas of the science if he thinks of value as at all a
thing or an
object, or even as anything which lies in a thing or object. Persons are thus led to speak of such a nonentity as
intrinsic value. There are, doubtless, qualities inherent in such a substance as gold or iron which influence its value; but the word Value, so far as it can be correctly used, merely expresses
the circumstance of its exchanging in a certain ratio for some other substance.
Value expresses Ratio of Exchange.
If a ton of pig-iron exchanges in a market for an ounce of standard gold, neither the iron is value nor the gold; nor is there value in the iron nor in the gold. The notion of value is concerned only in the
fact or circumstance of one exchanging for the other. Thus it is scientifically incorrect to say that the value of the ton of iron
is the ounce of gold: we thus convert value into a concrete thing; and it is, of course, equally incorrect to say that the value of the ounce of gold is the ton of iron. The more correct and safe expression is, that
the value of the ton of iron is equal to the value of the ounce of gold, or that their values are as one to one.
Value in exchange expresses nothing but a ratio, and the term should not be used in any other sense. To speak simply of the value of an ounce of gold is as absurd as to speak of the
ratio of the number seventeen. What is the ratio of the number seventeen? The question admits no answer, for there must be another number named in order to make a ratio; and the ratio will differ according to the number suggested. What is the value of iron compared with that of gold?—is an intelligible question. The answer consists in stating the ratio of the quantities exchanged.
Popular use of the term Value.
In the popular use of the word value no less than three distinct though connected meanings seem to be confused together. These may be described as
(1) Value in use;
(2) Esteem, or urgency of desire;
(3) Ratio of exchange.
Adam Smith, in the familiar passage already referred
to, distinguished between the first and the third meanings. He said,
*67 “The word value, it is to be observed, has two different meanings, and sometimes expresses the power of purchasing other goods which the possession of that object conveys. The one may be called ‘value in use;’ the other ‘value in exchange.’ The things which have the greatest value in use have frequently little or no value in exchange; and, on the contrary, those which have the greatest value in exchange have frequently little or no value in use. Nothing is more useful than water: but it will purchase scarce anything; scarce anything can be had in exchange for it. A diamond, on the contrary, has scarce any value in use; but a very great quantity of other goods may frequently be had in exchange for it.”
It is sufficiently plain that, when Smith speaks of water as being highly useful and yet devoid of purchasing power, he means
water in abundance, that is to say, water so abundantly supplied that it has exerted its full useful effect, or its
total utility. Water, when it becomes very scarce, as in a dry desert, acquires exceedingly great purchasing power. Thus Smith evidently means by value in use,
the total utility of a substance of which the degree of utility has sunk very low, because the want of such substance has been well nigh satisfied. By purchasing power he clearly means the ratio of exchange for other commodities. But here he fails to point out that the
quantity of goods received in exchange depends just as much upon the nature of the goods received, as on the nature of those given for them. In exchange for a diamond we can get a great quantity of iron, or corn, or paving stones, or other commodity of which there is abundance; but we can get very few rubies, sapphires, or other precious stones. Silver is of high purchasing power compared with zinc, or lead, or iron, but of small purchasing power compared with gold, platinum, or iridium. Yet we might well say in any case that diamond and silver are things of high value. Thus I am led to think that the word value is often used in reality to mean
intensity of desire or esteem for a thing. A silver ornament is a beautiful object apart from all ideas of traffic; it may thus be valued or esteemed simply because it suits the taste and fancy of its owner, and is the only one possessed. Even Robinson Crusoe must have looked upon each of his possessions with varying esteem and desire for more, although he was incapable of exchanging with any other person. Now, in this sense value seems to be identical with the final degree of utility of a commodity, as defined in a previous page (p. 49); it is measured by the intensity of the pleasure or benefit which would be obtained from a new increment of the same commodity. No doubt there is a close connection between value in this meaning, and value as ratio of exchange. Nothing can have a high purchasing power unless it be highly esteemed in itself; but it may be highly esteemed apart from all comparison
with other things; and, though highly esteemed, it may have a low purchasing power. because those things against which it is measured are still more esteemed.
Thus I come to the conclusion that, in the use of the word value, three distinct meanings are habitually confused together, and require to be thus distinguished—
(1) Value in use = total utility;
(2) Esteem = final degree of utility;
(3) Purchasing power = ratio of exchange.
It is not to be expected that we could profitably discuss such matters as economical doctrines, while the fundamental ideas of the subject are thus jumbled up together in one ambiguous word. The only thorough remedy consists in substituting for the dangerous name
value that one of three stated meanings which is intended in each case. In this work, therefore, I shall discontinue the use of the word value altogether, and when, as will be most often the case in the remainder of the book, I need to refer to the third meaning, often called by economists
exchange or exchangeable value, I shall substitute the wholly unequivocal expression
Ratio of exchange, specifying at the same time what are the
two articles exchanged. When we speak of the ratio of exchange of pig-iron and gold, there can be no possible doubt that we intend to refer to the ratio of the number of units of the one commodity to the
number of units of the other commodity for which it exchanges, the units being arbitrary concrete magnitudes, but the ratio an abstract number.
When I proposed, in the first edition of this book, to use Ratio of Exchange instead of the word value, the expression had been so little, if at all, employed by English economists, that it amounted to an innovation. J. S. Mill, indeed, in his chapters on Value, speaks once and again of things exchanging for each other “in the ratio of their cost of production;” but he always omits to say distinctly that exchange value is itself a matter of ratio. As to Ricardo, Malthus, Adam Smith, and other great English economists, although they usually discourse at some length upon the meanings of the word value, I am not aware that they ever explicitly apply the name
ratio to exchange or exchangeable value. Yet ratio is unquestionably the correct scientific term, and the only term which is strictly and entirely correct.
It is interesting, therefore, to find that, although overlooked by English economists, the expression had been used by two or more of the truly scientific French economists, namely, Le Trosne and Condillac. Le Trosne carefully defines value in the following terms:
*68 “La valeur consiste dans le rapport d’échange qui se trouve entre telle chose et telle autre, entre telle mesure d’une production et telle mesure des autres.” Condillac apparently adopts the words of
Le Trosne, saying
*69 of value: “Qu’elle consiste dans le rapport d’échange entre telle chose et telle autre.” Such economical works as those of Baudeau, Le Trosne, and Condillac were almost wholly unknown to English readers until attention was drawn to them by Mr. H. D. Mácleod and Professor Adamson; but I shall endeavour for the future to make proper use of them.
Dimension of Value.
There is no difficulty in seeing that, when we use the word Value in the sense of ratio of exchange, its dimension will be simply zero. Value will be expressed, like angular magnitude and other ratios in general, by abstract number. Angular magnitude is measured by the ratio of a line to a line, the ratio of the are subtended by the angle to the radius of the circle. So value in this sense is a ratio of the quantity of one commodity to the quantity of some other commodity exchanged for it. If we compare the commodities simply as physical quantities, we have the dimensions M divided by M, or MM
-1, or M
0. Exactly the same result would be obtained if, instead of taking the mere physical quantities, we were to compare their utilities, for we should then have MU divided by MU or M
0U
0, which, as it really means
unity, is identical in meaning with M
0.
When we use the word value in the sense of
esteem, or urgency of desire, the feeling with which Oliver Twist must have regarded a few more mouthfuls when he “asked for more,” the meaning of the word, as already explained, is identical with
degree of utility, of which the dimension is U. Lastly, the
value in use of Adam Smith, or the
total utility, is the integral of U
d M, and has the dimensions MU. We may thus tabulate our results concerning the ambiguous uses of the word
value—
| Popular Expression of Meaning. | Scientific Expression. | Dimensions. |
|---|---|---|
| (1) Value in use | Total Utility | MU. |
| (2) Esteem, or Urgency of Desire for more |
Final Degree of Utility | U. |
| (3) Purchasing Power | Ratio of Exchange | M 0. |
Definition of Market.
Before proceeding to the Theory of Exchange, it will be desirable to place beyond doubt the meanings of two other terms which I shall frequently employ.
By a
Market I shall mean much what commercial men use it to express. Originally a market was a public place in a town where provisions and other objects were exposed for sale; but the word has been generalised, so as to mean any body of persons who are in intimate business relations and carry on extensive transactions in any commodity. A great city may contain as many markets as there are important branches of trade, and these markets may or may not be localised. The central point of a market is the
public exchange,—mart or auction rooms, where the traders agree to meet and transact business. In London, the Stock Market, the Corn Market, the Coal Market, the Sugar Market, and many others, are distinctly localised; in Manchester, the Cotton Market, the Cotton Waste Market, and others. But this distinction of locality is not necessary. The traders may be spread over a whole town, or region of country, and yet make a market, if they are, by means of fairs, meetings, published price lists, the post office, or otherwise, in close communication with each other. Thus, the common expression
Money Market denotes no locality: it is applied to the aggregate of those bankers, capitalists, and other traders who lend or borrow money, and who constantly exchange information concerning the course of business.
*70
In Economics we may usefully adopt this term with a clear and well-defined meaning. By a market I shall mean two or more persons dealing in two or more commodities, whose stocks of those commodities and intentions of exchanging are known to all. It is also essential that the ratio of exchange between any
two persons should be known to all the others. It is only so far as this community of knowledge extends that the market extends. Any persons who are not acquainted at the moment with the prevailing ratio of exchange, or whose stocks are not available for want of communication, must not be considered part of the market. Secret or unknown stocks of a commodity must also be considered beyond reach of a market so long as they remain secret and unknown. Every individual must be considered as exchanging from a pure regard to his own requirements or private interests, and there must be perfectly free competition, so that any one will exchange with any one else for the slightest apparent advantage. There must be no conspiracies for absorbing and holding supplies to produce unnatural ratios of exchange. Were a conspiracy of farmers to withhold all corn from market, the consumers might be driven, by starvation, to pay prices bearing no proper relation to the existing supplies, and the ordinary conditions of the market would be thus overthrown.
The theoretical conception of a perfect market is more or less completely carried out in practice. It is the work of brokers in any extensive market to organise exchange, so that every purchase shall be made with the most thorough acquaintance with the conditions of the trade. Each broker strives to gain the best knowledge of the conditions of supply and demand, and the earliest intimation of any change. He is in communication with as many other traders
as possible, in order to have the widest range of information, and the greatest chance of making suitable exchanges. It is only thus that a definite market price can be ascertained at every moment, and varied according to the frequent news capable of affecting buyers and sellers. By the mediation of a body of brokers a complete
consensus is established, and the stock of every seller or the demand of every buyer brought into the market. It is of the very essence of trade to have wide and constant information. A market, then, is theoretically perfect only when all traders have perfect knowledge of the conditions of supply and demand, and the consequent ratio of exchange; and in such a market, as we shall now see, there can only be one ratio of exchange of one uniform commodity at any moment.
So essential is a knowledge of the real state of supply and demand to the smooth procedure of trade and the real good of the community, that I conceive it would be quite legitimate to compel the publication of any requisite statistics. Secrecy can only conduce to the profit of speculators who gain from great fluctuations of prices. Speculation is advantageous to the public only so far as it tends to equalise prices; and it is, therefore, against the public good to allow speculators to foster artificially the inequalities of prices by which they profit. The welfare of millions, both of consumers and producers, depends upon an accurate knowledge of the stocks of cotton and corn; and it would, therefore, be no
unwarrantable interference with the liberty of the subject to require any information as to the stocks in hand. In Billingsgate fish market there was long ago a regulation to the effect that salesmen shall fix up in a conspicuous place every morning a statement of the kind and amount of their stock.
*71 The same principle has long been recognised in the Acts of Parliament concerning the collection of statistics of the quantities and prices of corn sold in English market towns. More recently similar legislation has taken place as regards the cotton trade, in the Cotton Statistics Act of 1868. Publicity, whenever it can thus be enforced on markets by public authority, tends almost always to the advantage of everybody except perhaps a few speculators and financiers.
Definition of Trading Body.
I find it necessary to adopt some expression for any number of people whose aggregate influence in a market, either in the way of supply or demand, we have to consider. By a
trading body I mean, in the most general manner, any body either of buyers or sellers. The trading body may be a single individual in one case; it may be the whole inhabitants of a continent in another; it may be the individuals of a trade diffused through a country in a third. England and North America will be trading bodies if we are considering the corn we receive from
America in exchange for iron and other goods. The continent of Europe is a trading body as purchasing coal from England. The farmers of England are a trading body when they sell corn to the millers, and the millers both when they buy corn from the farmers and sell flour to the bakers.
We must use the expression with this wide meaning, because the principles of exchange are the same in nature, however wide or narrow may be the market considered. Every trading body is either an individual or an aggregate of individuals, and the law, in the case of the aggregate, must depend upon the fulfilment of law in the individuals. We cannot usually observe any precise and continuous variation in the wants and deeds of an individual, because the action of extraneous motives, or what would seem to be caprice, overwhelms minute tendencies. As I have already remarked (p. 15), a single individual does not vary his consumption of sugar, butter, or eggs from week to week by infinitesimal amounts, according to each small change in the price. He probably continues his ordinary consumption until accident directs his attention to a rise in price, and he then, perhaps, discontinues the use of the articles altogether for a time. But the aggregate, or what is the same, the average consumption, of a large community will be found to vary continuously or nearly so. The most minute tendencies make themselves apparent in a wide average. Thus, our laws of Economics will be theoretically true in the case of
individuals, and practically true in the case of large aggregates; but the general principles will be the same, whatever the extent of the trading body considered. We shall be justified, then, in using the expression with the utmost generality.
It should be remarked, however, that the economical laws representing the conduct of large aggregates of individuals will never represent exactly the conduct of any one individual. If we could imagine that there were a thousand individuals all exactly alike in regard to their demand for commodities, and their capabilities of supplying them, then the average laws of supply and demand deduced from the conduct of such individuals would agree with the conduct of any one individual. But a community is composed of persons differing widely in their powers, wants, habits, and possessions. In such circumstances the average laws applying to them will come under what I have elsewhere
*72 called the “Fictitious Mean,” that is to say, they are numerical results which do not pretend to represent the character of any existing thing. But average laws would not on this account be less useful, if we could obtain them; for the movements of trade and industry depend upon averages and aggregates, not upon the whims of individuals.
The Law of Indifference.
When a commodity is perfectly uniform or homogeneous
in quality, any portion may be indifferently used in place of an equal portion: hence, in the same market, and at the same moment, all portions must be exchanged at the same ratio. There can be no reason why a person should treat exactly similar things differently, and the slightest excess in what is demanded for one over the other will cause him to take the latter instead of the former. In nicely-balanced exchanges it is a very minute scruple which turns the scale and governs the choice. A minute difference of quality in a commodity may thus give rise to preference, and cause the ratio of exchange to differ. But where no difference exists at all, or where no difference is known to exist, there can be no ground for preference whatever. If, in selling a quantity of perfectly equal and uniform barrels of flour, a merchant arbitrarily fixed different prices on them, a purchaser would of course select the cheaper ones; and where there was absolutely no difference in the thing purchased, even an excess of a penny in the price of a thing worth a thousand pounds would be a valid ground of choice. Hence follows what is undoubtedly true, with proper explanations, that
in the same open market, at any one moment, there cannot be two prices for the same kind of article. Such differences as may practically occur arise from extraneous circumstances, such as the defective credit of the purchasers, their imperfect knowledge of the market, and so on.
The principle above expressed is a general law of
the utmost importance in Economics, and I propose to call it
The Law of Indifference, meaning that, when two objects or commodities are subject to no important difference as regards the purpose in view, they will either of them be taken instead of the other with perfect indifference by a purchaser. Every such act of indifferent choice gives rise to an equation of degrees of utility, so that in this principle of indifference we have one of the central pivots of the theory.
Though the price of the same commodity must be uniform at any one moment, it may vary from moment to moment, and must be conceived as in a state of continual change. Theoretically speaking, it would not usually be possible to buy two portions of the same commodity
successively at the same ratio of exchange, because, no sooner would the first portion have been bought than the conditions of utility would be altered. When exchanges are made on a large scale, this result will be verified in practice.
*73 If a wealthy person invested £100,000 in the funds in the morning, it is hardly likely that the operation could be repeated in the afternoon at the same price. In any market, if a person goes on buying largely, he will ultimately
raise the price against himself. Thus it is apparent that extensive purchases would best be made gradually, so as to secure the advantage of a lower price upon the earlier portions. In theory this effect of exchange upon the ratio of exchange must be conceived to exist in some degree, however small may be the purchases made. Strictly speaking, the ratio of exchange at any moment is that of
dy to
dx, of an infinitely small quantity of one commodity to the infinitely small quantity of another which is given for it. The ratio of exchange is really a differential coefficient. The quantity of any article purchased is a function of the price at which it is purchased, and the ratio of exchange expresses the rate at which the quantity of the article increases compared with what is given for it.
We must carefully distinguish, at the same time, between the Statics and Dynamics of this subject. The real condition of industry is one of perpetual motion and change. Commodities are being continually manufactured and exchanged and consumed. If we wished to have a complete solution of the problem in all its natural complexity, we should have to treat it as a problem of motion—a problem of dynamics. But it would surely be absurd to attempt the more difficult question when the more easy one is yet so imperfectly within our power. It is only as a purely statical problem that I can venture to treat the action of exchange. Holders of commodities will be regarded not as continuously passing on these commodities in
streams of trade, but as possessing certain fixed amounts which they exchange until they come to equilibrium.
It is much more easy to determine the point at which a pendulum will come to rest than to calculate the velocity at which it will move when displaced from that point of rest. Just so, it is a far more easy task to lay down the conditions under which trade is completed and interchange ceases, than to attempt to ascertain at what rate trade will go on when equilibrium is not attained.
The difference will present itself in this form: dynamically we could not treat the ratio of exchange otherwise than as the ratio of
dy and
dx, infinitesimal quantities of commodity. Our equations would then be regarded as differential equations, which would have to be integrated. But in the statical view of the question we can substitute the ratio of the finite quantities
y and
x. Thus, from the self-evident principle, stated on pp. 91, 92, that there cannot, in the same market, at the same moment, be two different prices for the same uniform commodity, it follows that
the last increments in an act of exchange must be exchanged in the same ratio as the whole quantities exchanged. Suppose that two commodities are bartered in the ratio of
x for
y; then every
mth part of
x is given for the
mth part of
y, and it does not matter for which of the
mth parts. No part of the commodity can be treated differently to any other part. We may carry this division to an indefinite
extent by imagining
m to be constantly increased, so that, at the limit, even an infinitely small part of
x must be exchanged for an infinitely small part of
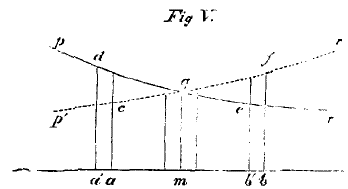
y, in the same ratio as the whole quantities. This result we may express by stating that the increments concerned in the process of exchange must obey the equation
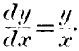
The use which we shall make of this equation will be seen in the next section.
The Theory of Exchange.
The keystone of the whole Theory of Exchange, and of the principal problems of Economics, lies in this proposition—
The ratio of exchange of any two commodities will be the reciprocal of the ratio of the final degrees of utility of the quantities of commodity available for consumption after the exchange is completed. When the reader has reflected a little upon the meaning of this proposition, he will see, I think, that it is necessarily true, if the principles of human nature have been correctly represented in previous pages.
Imagine that there is one trading body possessing only corn, and another possessing only beef. It is certain that, under these circumstances, a portion of the corn may be given in exchange for a portion of the beef with a considerable increase of utility. How are we to determine at what point the exchange will
cease to be beneficial? This question must involve both the ratio of exchange and the degrees of utility. Suppose, for a moment, that the ratio of exchange is approximately that of ten pounds of corn for one pound of beef: then if, to the trading body which possesses corn, ten pounds of corn are less useful than one of beef, that body will desire to carry the exchange further. Should the other body possessing beef find one pound less useful than ten pounds of corn, this body will also be desirous to continue the exchange. Exchange will thus go on until each party has obtained all the benefit that is possible, and loss of utility would result if more were exchanged. Both parties, then, rest in satisfaction and equilibrium, and the degrees of utility have come to their level, as it were.
This point of equilibrium will be known by the criterion, that an infinitely small amount of commodity exchanged in addition, at the same rate, will bring neither gain nor loss of utility. In other words, if increments of commodities be exchanged at the established ratio, their utilities will be equal for both parties. Thus, if ten pounds of corn were of exactly the same utility as one pound of beef, there would be neither harm nor good in further exchange at this ratio.
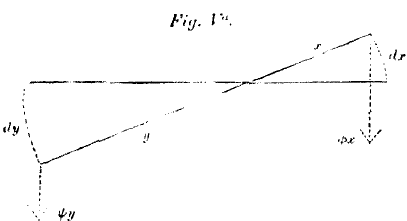
 It is hardly possible to represent this theory completely by means of a diagram, but the accompanying figure may, perhaps, render it clearer. Suppose the line
It is hardly possible to represent this theory completely by means of a diagram, but the accompanying figure may, perhaps, render it clearer. Suppose the line
pqr to be a small portion of the curve
of utility of one commodity, while the broken line
p‘
qr‘ is the like curve of another commodity which has been reversed and superposed on the other. Owing to this reversal, the quantities of the first commodity are measured along the base line from
a towards
b, whereas those of the second must be measured in the opposite direction. Let units of both commodities be represented by equal lengths: then the little line
áa indicates an increase of the first commodity, and a decrease of the second. Assume the ratio of exchange to be that of unit for unit, or 1 to 1: then, by receiving the commodity
áa the person will gain the utility
ad, and lose the utility
ác; or he will make a net gain of the utility corresponding to the mixtilinear figure
cd. He will, therefore, wish to extend the exchange. If he were to go up to the point
b’, and were still proceeding, he would, by the next small exchange, receive the utility
be, and part with
b’f; or he would have a net loss of
ef. He would, therefore, have gone too far; and it is pretty obvious that the point of intersection,
q, defines the place where he would stop with the greatest
advantage. It is there that a net gain is converted into a net loss, or rather where, for an infinitely small quantity, there is neither gain nor loss. To represent an infinitely small quantity, or even an exceedingly small quantity, on a diagram is, of course, impossible; but on either side of the line
mq I have represented the utilities of a small quantity of commodity more or less, and it is apparent that the net gain or loss upon the exchange of these quantities would be trifling.
Symbolic Statement of the Theory.
To represent this process of reasoning in symbols, let
Dx denote a small increment of corn, and
Dy a small increment of beef exchanged for it. Now our Law of Indifference comes into play. As both the corn and the beef are homogeneous commodities, no parts can be exchanged at a different ratio from other parts in the same market: hence, if
x be the whole quantity of corn given for
y, the whole quantity of beef received,
Dy must have the same ratio to
Dx as
y to
x: we have then,
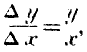 or
or 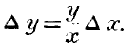
In a state of equilibrium, the utilities of these increments must be equal in the case of each party, in order that neither more nor less exchange would be desirable. Now the increment of beef,
Dy, is
y/
xtimes as great as the increment of corn,
Dx, so that, in order that their utilities shall be equal, the degree of utility of beef must be
x/
y times as great as the degree of utility of corn. Thus we arrive at the principle that
the degrees of utility of commodities exchanged will be in the inverse proportion of the magnitudes of the increments exchanged.
Let us now suppose that the first body, A, originally possessed the quantity
a of corn, and that the second body, B, possessed the quantity
b of beef. As the exchange consists in giving
x of corn for
y of beef, the state of things after exchange will be as follows:—
A holds
a –
x of corn, and
y of beef.
B holds
x of corn, and
b –
y of beef.
Let
f1 (
a –
x) denote the final degree of utility of corn to A, and
f2x the corresponding function for B. Also let
y1y denote A’s final degree of utility for beef, and
y2 (
b –
y) B’s similar function. Then, as explained on p. 96, A will not be satisfied unless the following equation holds true:—
a –
x).
dx =
y1y.dy;

Hence, substituting for the second member by the equation given on p. 95, we have
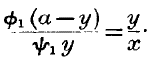
What holds true of A will also hold true of B,
mutatis mutandis. He must also derive exactly equal utility from the final increments, otherwise it will be for his interest to exchange either more or less, and he will disturb the conditions of exchange. Accordingly the following equation must hold true:—
b –
y).
dy =
f2x.dx:
or, substituting as before,
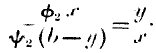
We arrive, then, at the conclusion, that whenever two commodities are exchanged for each other, and
more or less can be given or received in infinitely small quantities, the quantities exchanged satisfy two equations, which may be thus stated in a concise form—

The two equations are sufficient to determine the results of exchange; for there are only two unknown quantities concerned, namely,
x and
y, the quantities given and received.
A vague notion has existed in the minds of economical writers, that the conditions of exchange may be expressed in the form of an equation. Thus, J. S. Mill has said:
*74 “The idea of a
ratio, as between demand and supply, is out of place, and has no concern in the matter: the proper mathematical analogy is that of an
equation. Demand and supply, the quantity demanded and the quantity supplied, will be
made equal.” Mill here speaks of an equation as only a proper mathematical
analogy. But if Economics is to be a real science at all, it must not deal merely with analogies; it must reason by real equations, like all the other sciences which have reached at all a systematic character. Mill’s equation, indeed, is not explicitly the same as any at which we have arrived above. His equation states that the quantity of a commodity given by A is equal to the quantity received by B. This seems at first sight to be a mere truism, for this equality must necessarily exist if any exchange takes place at all. The theory of value, as expounded by Mill, fails to reach the root of the matter, and show how the amount of demand or supply is caused to vary. And Mill does not perceive that, as there must be two parties and two quantities to every exchange, there must be two equations.
Nevertheless, our theory is perfectly consistent with the laws of supply and demand; and if we had the functions of utility determined, it would be possible to throw them into a form clearly expressing the equivalence of supply and demand. We may regard
x as the quantity demanded on one side and supplied on the other; similarly,
y is the quantity supplied on the one side and demanded on the other. Now, when we hold the two equations to be simultaneously true, we assume that the
x and
y of one equation equal those of the other. The laws of supply and demand are thus a result of what seems to me the true theory of value or exchange.
Analogy to the Theory of the Lever.
I have heard objections made to the general character of the equations employed in this book. It is remarked that the equations in question continually involve infinitesimal quantities, and yet they are not treated as differential equations usually are, that is integrated. There is, indeed, no reason why the process of integration should not be applied when it is required, and I will here show that the equations employed do not differ in general character from those which are really treated in many branches of physical science. Whenever, in fact, we deal with continuously varying quantities, the ultimate equations must lie between infinitesimals. The process of integration, if I understand the matter aright, only ascertains other equations, the truth of which follows from the fundamental differential equation.
The mode in which mechanies is usually treated in elementary work tends to disguise the real foundation of the science which is to be found in the so-called
theory of virtual velocities. Let us take the description of the lever of the first order as it is given in some of the best modern elementary works, as, for instance, in Mr. Magnus’s
Lessons in Elementary Mechanics, p. 128. We here read as follows:—
“Let
AB be a lever turning freely about
C, the fulcrum, and let
P be the force applied at
A, and
W the force exerted, or resistance overcome, or weight
raised at
B. Suppose the lever turned through the angle
ACA‘, then the work done by
P equals
P × are
AA‘, and work done by
W equals
W × arc
BB‘, if
P and
W act perpendicularly to the arm. Therefore, by the law of energy,
AA‘ =
W ×
BB‘, and since
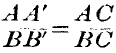 we have
we haveAC =
W ×
BC,
P × its arm =
W × its arm.”
Now, in such a statement as this, we seem to be dealing with plain finite quantities, and there is no apparent difficulty in the matter. In reality the difficulty is only disguised by assuming that
P and
W act perpendicularly to the arm through finite arcs. This condition is, indeed, carried out with approximate exactness in the problem of the wheel and axle,
*75 which may be regarded as combining together an infinite series of straight levers, coming successively into operation. In this machine, therefore, the weights, roughly speaking, always act perpendicularly to arms of invariable length. But, in the generality of cases of the lever, the theory is only true for infinitely small displacements, and no sooner has the lever begun to move through any finite arc
AA‘, than it ceases to be exactly true that the work done by
P equals
P × arc
AA‘. Nevertheless, the theory is quite correct as applied to the lever considered statically, that is, as in a state of
rest and equilibrium, because the finite arcs of displacement, when it really is displaced, are exactly proportional to the infinitely small arcs, known as virtual velocities, through which it would be displaced, if instead of being at rest, it suffered an infinitely small displacement.
It is curious, moreover, that, when we take the theory of the lever treated according to the principle of virtual velocities, we get equations exactly similar in form to those of the theory of value as established above. The general principle of virtual velocities is to the effect that, if any number of forces be in equilibrium at one or more points of a rigid body, and if this body receive an infinitely small displacement, the algebraic sum of the products of each force into its displacement is equal to zero. In the case of a lever of the first order, this amounts to saying that one force multiplied into its displacement will be neutralised by the other force multiplied into its
negative displacement. But inasmuch as the displacements are exactly proportional to the lengths of the arms of the lever, we obtain as a derivative equation, that the forces multiplied each by its own arm are equal to each other. No doubt in the quotation given above,
P ×
AC =
W ×
BC is an equation between finite quantities; but the real equation derived immediately from the principle of virtual velocities, is
P ×
AA‘ =
W ×
BB‘, in which
P and
W are finite, but
AA‘ and
BB‘ are in strictness infinitely small displacements. Let us write this
equation in the form
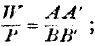
then as we also have
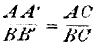
we can substitute; hence
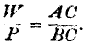
I dwell upon this matter at some length because we here have exactly the forms of the equations of exchange. As we have seen, the original equation is of the general form
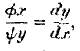
where
fx and
yy represent finite expressions for the degrees of utility of the commodities
Y and
X, as regards some individual, and
dy and
dx are infinitesimal quantities of those commodities exchanged. But these infinitesimals may in this case at least be eliminated, because, in virtue of the Law of Indifference, they are exactly proportional to the whole finite quantities exchanged. Hence for
dy/
dx we substitute
y/
x. We may write the equations one below the other, so as to make the analogy visible—thus
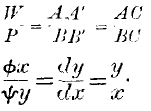
To put this analogy of the theories of exchange and of the lever in the clearest possible light, I give below a diagram, in which the several economic qualities are represented by the parts of the diagram to which they correspond or are proportional.
Now in statical problems no such process as integration is applicable. The equation lies actually
between imaginary infinitesimal quantities, and there is no effect to be summed up. Yet there is no statical problem which is not subject to the principle of virtual velocities, and Poisson, in his
Traité de Mécanique, which commences with statical theorems, asserts explicitly,
*76 “Dans cet ouvrage, j’emploierai exclusivement la méthode
des infiniment petits.“
Impediments to Exchange.
We have hitherto treated the theory of exchange as if the action of exchange could be carried on without trouble or cost. In reality, the cost of conveyance is almost always of importance, and it is sometimes the principal element in the question. To the cost of mere transport must be added a variety of charges of brokers, agents, packers, dock, harbour, light dues, etc., together with any customs duties imposed either on the importation or exportation of commodities. All these charges, whether necessary
or arbitrary, are so many impediments to commerce, and tend to reduce its advantages. The effect of any one such charge, or of the aggregate of the costs of exchange, can be represented in our formulæ in a very simple manner.
In whatever mode the charges are payable, they may be conceived as paid by the surrender on importation of a certain fraction of the commodity received; for the amount of the charges will usually be proportional to the quantity of goods, and, if expressed in money, can be considered as turned into commodity.
Thus, if A gives
x in exchange, this is not the quantity received by B; a part of
x is previously subtracted, so that B receives say
mx, which is less than
x, and the terms of exchange must be adjusted on his part so as to agree with this condition. Hence the second equation will be
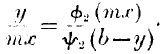
Again, A, though giving
x, will not receive the whole of
y; but say
ny, so that his equation similarly will be
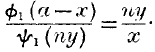
The result is, that there is not one ratio of exchange, but two ratios; and the more these differ, the less advantage will there be in exchange. It is obvious that A has either to remain satisfied with less of the second commodity than before, or has to give more
of his own in purchasing it. By an obvious transfer of the factors
m and
n we may state the equations of impeded exchange in the concise form—
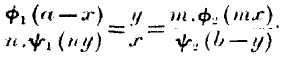
Illustrations of the Theory of Exchange.
As stated above, the Theory of Exchange may seem to be of a somewhat abstract and perplexing character; but it is not difficult to find practical illustrations which will show how it is verified in the actual working of a great market. The ordinary laws of supply and demand, when properly stated, are the practical manifestation of the theory. Considerable discussion has taken place concerning these laws, in consequence of Mr. W. T. Thornton’s writings upon the subject in the
Fortnightly Review, and in his work on the
Claims of Labour. Mill, although he had previously declared the Theory of Value to be complete and perfect (see p. 76), was led by Mr. Thornton’s arguments to allow that modification was required.
For my own part, I think that most of Mr. Thornton’s arguments are beside the question. He suggests that there are no regular laws of supply and demand, because he adduces certain cases in which no regular variation can take place. Those cases might be indefinitely multiplied, and yet the laws in question would not be touched. Of course, laws which assume
a continuity of variation are inapplicable where continuous variation is impossible. Economists can never be free from difficulties unless they will distinguish between a theory and the
application of a theory. Because, in retail trade, in English or Dutch auction, or other particular modes of traffic, we cannot at once observe the operation of the laws of supply and demand, it is not in the least to be supposed that those laws are false. In fact, Mr. Thornton seems to allow that, if prospective demand and supply are taken into account, they become substantially true. But, in the actual working of any market, the influence of future events should never be neglected, neither by a merchant nor an economist.
Though Mr. Thornton’s objections are mostly beside the question, his remarks have served to show that the action of the laws of supply and demand was inadequately explained by previous economists. What constitutes the demand and the supply was not carefully enough investigated. As Mr. Thornton points out, there may be a number of persons willing to buy; but if their highest offer is ever so little short of the lowest price which the seller is willing to take, their influence is
nil. If in an auction there are ten people willing to buy a horse at £20, but not higher, their demand instantly ceases when any one person offers £21. I am inclined not only to accept such a view, but to carry it further. Any change in the price of an article will be determined not with regard to the large numbers who might or might not buy it
at other prices, but by the few who will or will not buy it according as a change is made close to the existing price.
The theory consists in carrying out this view to the point of asserting that it is only comparatively insignificant quantities of supply and demand which are at any moment operative on the ratio of exchange. This is practically verified by what takes place in any very large market—say that of the Consolidated Three Per Cent Annuities. As the whole amount of the English funds is nearly eight hundred millions sterling, the quantity bought or sold by any ordinary purchaser is inconsiderably small in comparison. Even £1000 worth of stock may be taken as an infinitesimally small increment, because it does not appreciably affect the total existing supply. Now the theory consists in asserting that the market price of the funds is affected from hour to hour not by the enormous amounts which
might be bought or sold at extreme prices, but by the comparatively insignificant amounts which
are being sold or bought at the existing prices. A change of price is always occasioned by the overbalancing of the inclinations of those who will or will not sell just about the point at which prices stand. When Consols are at 93½, and business is in a tranquil state, it matters not how many buyers there are at 93, or sellers at 94. They are really off the market. Those only are operative who may be made to buy or sell by a rise or fall of an eighth. The question is, whether the price shall remain at 93½,
or rise to 93 5/8, or fall to 93 3/8. This is determined by the sale or purchase of comparatively very small amounts. It is the purchasers who find a little stock more profitable to them than the corresponding sum of money who make the price rise by 1/8. When the price of the funds is very steady and the market quiescent, it means that the stocks are distributed among holders in such a way that the exchange of more or less at the prevailing price is a matter of indifference.
In practice, no market ever long fulfils the theoretical conditions of equilibrium, because, from the various accidents of life and business, there are sure to be people every day compelled to sell, or having sudden inducements to buy. There is nearly always, again, the influence of prospective supply or demand, depending upon the political intelligence of the moment. Speculation complicates the action of the laws of supply and demand in a high degree, but does not in the least degree arrest their action or alter their nature. We shall never have a Science of Economics unless we learn to discern the operation of law even among the most perplexing complications and apparent interruptions.
Problems in the Theory of Exchange.
We have hitherto considered only one simple case of the Theory of Exchange. In all other cases where the commodities are capable of indefinite subdivision,
the principles will be exactly the same, but the particular conditions may be subject to variation.
We may, firstly, express the conditions of a great market where vast quantities of some stock are available, so that any one small trader will not appreciably affect the ratio of exchange. This ratio is, then, approximately a fixed number, and each trader exchanges at that ratio just so much as suits him. These circumstances may be represented by supposing A to be a trading body possessing two very large stocks of commodities,
a and
b. Let C be a person who possesses a comparatively small quantity
c of the second commodity, and gives a portion of it,
y, which is very small compared with
b, in exchange for a portion
x of
a, which is very small compared with
a. Then, after exchange, we shall find A in possession of the quantities
a –
x and
b +
y, and C in possession of
x and
c –
y. The equations will become
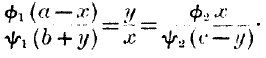
Since
a –
x and
b +
y, by supposition, do not appreciably differ from
a and
b, we may substitute the latter quantities, and we have, for the first equation, approximately,
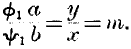
The ratio of exchange being an approximately fixed ratio determined by the conditions of the trading body A, there is, in reality, only one undetermined quantity,
x, the quantity of commodity which C finds
it advantageous to purchase by expending part of
c. This will now be determined by the equation
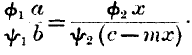
This equation will represent the condition in regard to any one distinct commodity of a very small country trading with a much larger one. It might represent, to some extent, the circumstances of trade between the Channel Islands and the great markets of England, though, of course, it is never absolutely verified, because the smallest purchasers do affect the market in some degree. The equation still more accurately represents the position of an individual consumer with regard to the aggregate trade of a large community, since he must buy at the current prices, which he cannot in an appreciable degree affect.
A still simpler formula, however, is needed to represent the conditions of a large part of our purchases. In many cases we want so little of a commodity, that an individual need not give more than a very small fraction of his possessions to obtain it. We may suppose, then, that
y in the last problem is a very small part of
c, so that
y2 (
c –
y) does not differ appreciably from
y2c. Taking
m as before to be the existing ratio of exchange, we have only one equation—
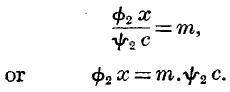
This means that C will buy of the commodity until its degree of utility falls below that of the commodity he gives. A person’s expenditure on salt is in this country an inconsiderable item of expense; what he thus spends does not make him appreciably poorer; yet, if the established price or ratio is one penny for each pound of salt, he buys in any time, say one year, so many pounds of salt that an additional pound would not have so much utility to him as a penny. In the above equation
m.y2c represents the utility to him of a penny, which being an inconsiderable fraction of his possessions, is approximately invariable in utility, and he buys salt until
f2x, which is approximately the utility of the next pound, is equal to, or it may be somewhat less than that of the penny. But this case must not be confused with that of purchases which appreciably affect the possessions of the purchaser. Thus, if a poor family purchase much butchers’-meat, they will probably have to go without something else. The more they buy, the lower the final degree of utility of the meat, and
the higher the final degree of utility of something else; and thus these purchases will be the more narrowly limited.
Complex Cases of the Theory.
We have hitherto considered the Theory of Exchange as applying only to two trading bodies possessing and dealing in two commodities. Exactly the same principles hold true, however numerous and
complicated may be the conditions. The main point to be remembered in tracing out the results of the theory is, that the same pair of commodities in the same market can have only one ratio of exchange, which must therefore prevail between each body and each other, the costs of conveyance being considered as
nil. The equations become rapidly more numerous as additional bodies or commodities are considered; but we may exhibit them as they apply to the case of three trading bodies and three commodities.
Thus, suppose that
A possesses the stock
a of cotton, and gives
x1 of it to B,
x2 to C.
B possesses the stock
b of silk, and gives
y1 to A,
y2 to C.
C possesses the stock
c of wool, and gives
z1 to A,
z2 to B.
We have here altogether six unknown quantities—
x1,
x2,
y1,
y2,
z1,
z2; but we have also sufficient means of determining them. They are exchanged as follows—
A gives
x1 for
y1, and
x2 for
z1.
B gives ‘
y1 for
x1, and
y2 for
z2.
C gives
z1 for
x2, and
z2 for
y2.
These may be treated as independent exchanges; each body must be satisfied in regard to each of its exchanges, and we must therefore take into account the functions of utility or the final degrees of utility of each commodity in respect of each body. Let us express these functions as follows—
| f1, y1, c1 are the respective functions of utility for |
A. |
| f2, y2, c2 are the respective functions of utility for |
B. |
| f3, y3, c3 are the respective functions of utility for |
C. |
Now A, after the exchange, will hold
a –
x1 –
x2 of cotton and
y1 of silk; and B will hold
x1 of cotton and
b –
y1 –
y2 of silk: their ratio of exchange,
y1 for
x1, will therefore be governed by the following pair of equations:—
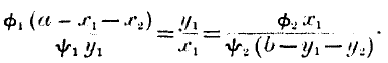
The exchange of A with C will be similarly determined by the ratio of the degrees of utility of wool and cotton on each side subsequent to the exchange; hence we have

There will also be interchange between B and C which will be independently regulated on similar principles, so that we have another pair of equations to complete the conditions, namely—
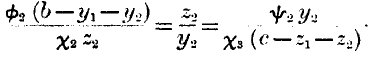
We might proceed in the same way to lay down the conditions of exchange between more numerous bodies, but the principles would be exactly the same. For every quantity of commodity which is given in exchange something must be received; and if portions of the same kind of commodity be received from several distinct parties, then we may conceive the
quantity which is given for that commodity to be broken up into as many distinct portions. The exchanges in the most complicated case may thus always be decomposed into simple exchanges, and every exchange will give rise to two equations sufficient to determine the quantities involved. The same can also be done when there are two or more commodities in the possession of each trading body.
Competition in Exchange.
One case of the Theory of Exchange is of considerable importance, and arises when two parties compete together in supplying a third party with a certain commodity. Thus, suppose that A, with the quantity of one commodity denoted by
a, purchases another kind of commodity both from B and from C, who respectively possess
b and
c of it. All the quantities concerned are as follows—
A gives
x1 of
a to B and
x2 to C,
B gives
y1 of
b to A,
C gives
y2 of
c to A.
As each commodity may be supposed to be perfectly homogeneous, the ratio of exchange must be the same in one case as in the other, so that we have one equation thus furnished—
 |
(1) |
Now, provided that A gets the right commodity in the proper quantity, he does not care whence it
comes, so that we need not, in his equation, distinguish the source or destination of the quantities; he simply gives
x1 +
x2, and receives in exchange
y1 +
y2. Observing, then, that by (1)

we have the usual equation of exchange—
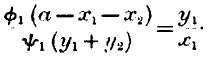 |
(2) |
But B and C must both be separately satisfied with their shares in the transaction. Thus
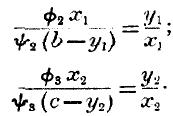 |
(3)
(4) |
There are altogether four unknown quantities—
x1,
x2,
y1,
y2; and we have four equations by which to determine them. Various suppositions might be made as to the comparative magnitudes of the quantities
b and
c, or the character of the functions concerned; and conclusions could then be drawn as to the effect upon the trade. The general result would be, that the smaller holder must more or less conform to the prices of the larger holder.
Failure of the Equations of Exchange.
Cases constantly occur in which equations of the kind set forth in the preceding pages fail to hold
true, or lead to impossible results. Such failure may indicate that no exchange at all takes place, but it may also have a different meaning.
In the first case, it may happen that the commodity possessed by A has a high degree of utility to A, and a low degree to B, and that
vice versâ B’s commodity has a high degree of utility to B and less to A. This difference of utility might exist to such an extent, that though B were to receive very little of A’s commodity, yet the final degree of utility to him would be less than that of his own commodity, of which he enjoys much more. In such a case no benefit can arise from exchange, and no exchange will consequently take place. This failure of exchange will be indicated by a failure of the equations.
It may also happen that the whole quantities of commodity possessed are exchanged, and yet the equations fail. A may have so low a desire for consuming his own commodity, that the very last increment of it has less degree of utility to him than a small addition to the commodity received in exchange. The same state of things might happen to exist with B as regards his commodity: under these circumstances the whole possessions of one might be exchanged for the whole of the other, and the ratio of exchange would of course be defined by the ratio of these quantities. Yet each party might desire the last increment of the commodity received more than he desires the last increment of that given, so that the equations would fail to be true. This case will
hardly occur practically in international trade, since two nations usually trade in many commodities, a fact which would alter the conditions.
Again, the equations of exchange will fail to be possible when the commodity or useful article possessed on one or both sides is indivisible. We have always assumed hitherto that more or less of a commodity may be had, down to infinitely small quantities. This is approximately true of all ordinary trade, especially international trade between great industrial nations. Any one sack of corn or any one bar of iron is practically infinitesimal compared with the quantities exchanged by America and England; and even one cargo or parcel of corn or iron is a small fraction of the whole. But, in exceptional cases, even international trade might involve indivisible articles. We might conceive the British Government giving the Koh-i-noor diamond to the Khedive of Egypt in exchange for Pompey’s Pillar, in which case it would certainly not answer the purpose to break up one article or the other.
*77 When an island or portion of territory is transferred from one possessor to another, it is often necessary to take the whole, or none.
America, in purchasing Alaska from Russia, would hardly have consented to purchase less than the whole. In every sale of a house, factory, or other building, it is usually impracticable to make any division without greatly lessening the utility of the whole. In all such cases our equations must fail to exist, because we cannot contemplate the existence of an increment or a decrement to an indivisible article.
Suppose, for example, that A and B each possess a book: they cannot break up the books, and must therefore exchange them entire, if at all. Under what conditions will they do so? Plainly on the condition that each makes a gain of utility by so doing. Here we deal not with the final degree of utility depending on an infinitesimal quantity, but on the
whole utility of the complete article. Now let us assign the symbols as follows:—
| u1 = the | utility of | A’s book to A, |
| u2 = the | utility of | A’s book to B, |
| v1 = the | utility of | B’s book to A, |
| v2 = the | utility of | B’s book to B. |
Then the conditions of exchange are simply
u1,
u2>
v2.
We might indeed theoretically contemplate the case where the utilities were exactly equal on one side; thus
u1,
u2 =
v2;
B would then be wholly indifferent to the exchange,
and I do not see any means of deciding whether he would or would not consent to it. But we need hardly consider the case, as it could seldom practically occur. Were the utilities exactly equal on both sides in respect to both objects, there would obviously be no motive to exchange. Again, the slightest loss of utility on either side would be a complete bar to the transaction, because we are not supposing, at present, that any other commodities are in possession so as to allow of separate inducements, or that any other motives than such as arise out of simple desire of one’s own convenience enter into the question.
A much more difficult problem arises when we suppose an indivisible article exchanged for a divisible commodity. When Russia sold Alaska this was a practically indivisible thing; but it was bought with money of which more or less might be given to indefinitely small quantities. A bargain of this kind is exceedingly common; indeed it occurs in the case of every house, mansion, estate, factory, ship, or other complete whole, which is sold for money. Our former equations of exchange certainly fail, for they involve increments of commodity on both sides. The theory seems to give a very unsatisfactory answer, for the problem proves to be, within certain limits, indeterminate.
Let X be the indivisible article;
u1 its utility to its possessor A, and
u2 its utility to B. Let
y be the quantity of commodity given for it, a commodity which is supposed to be divisible
ad infinitum; let
v1be the total utility of
y to A, and
v2 its total utility to B. Then it is quite evident that, in order to give rise to exchange,
v1 must be greater than
u1, and
u2 must be greater than
v2; that is, there must, as before, be a gain of utility on each side. The quantity
y must not be so great then as to deprive B of gain, nor so small as to deprive A of gain. The following is an extract from Mr. Thornton’s work which exactly expresses the problem:—
“There are two opposite extremes—one above which the price of a commodity cannot rise, the other below which it cannot fall. The upper of these limits is marked by the utility, real or supposed, of the commodity to the customer; the lower, of its utility to the dealer. No one will give for a commodity a quantity of money or money’s worth, which, in his opinion, would be of more use to him than the commodity itself. No one will take for a commodity a quantity of money or of anything else which he thinks would be of less use to himself than the commodity. The price eventually given and taken may be either at one of the opposite extremes, or may be anywhere intermediate between them.”
*78
Three distinct cases might occur, which can best be illustrated by a concrete example. Suppose we can read the thoughts of the parties in the sale of a house. If A says £1200 is the least price which will satisfy him, and B holds that £800 is the highest price which
it will be profitable for him to give, no exchange can possibly take place. If A should find £1000 to be his lowest limit, while B happens to name the same sum for his highest limit, the transaction can be closed, and the price will be exactly defined. But supposing, finally, that A is really willing to sell at £900, and B is prepared to buy at £1100, in what manner can we theoretically determine the price? I see no mode of solving the question. Any price between £900 and £1100 will leave a profit on each side, and both parties will lose if they do not come to terms. I conceive that such a transaction must be settled upon other than strictly economical grounds. The result of the bargain will greatly depend upon the comparative amount of knowledge of each other’s positions and needs which either bargainer may possess or manage to obtain in the course of the transaction. Thus the power of reading another man’s thoughts is of high importance in business, and the art of bargaining mainly consists in the buyer ascertaining the lowest price at which the seller is willing to part with his object, without disclosing if possible the highest price which he, the seller, is willing to give. The disposition and force of character of the parties, their comparative persistency, their adroitness and experience in business, or it may be feelings of justice or of kindliness, will also influence the decision. These are motives more or less extraneous to a theory of Economics, and yet they appear necessary considerations in this problem. It may be that indeterminate
bargains of this kind are best arranged by an arbitrator or third party.
The equations of exchange may fail again when commodities are divisible, but not to infinitely small quantities. There is always, in retail trade, a convenient unit below which we do not descend in purchases. Paper may be bought in quires, or even in packets, which it may not be desirable to break up. Wine cannot be bought from the wine merchant in less than a bottle at a time. In all such cases exchange cannot, theoretically speaking, be perfectly adjusted, because it will be infinitely improbable that an integral number of units will precisely verify the equations of exchange. In a large proportion of cases, indeed, the unit may be so small compared with the whole quantities exchanged as practically to be infinitely small. But suppose that a person be buying ink which is only to be had, under the circumstances, in one shilling bottles. If one bottle be not quite enough, how will he decide whether to take a second or not? Clearly by estimating the aggregate utility of the bottle of ink compared with the shilling. If there be an excess, he will certainly purchase it, and proceed to consider whether a third be desirable or not.
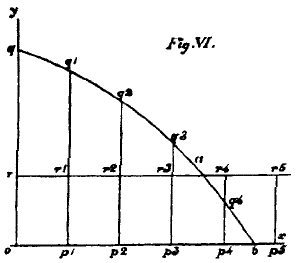 This case might be illustrated by Fig. VI., in which the spaces
This case might be illustrated by Fig. VI., in which the spaces
o q1,
p1q2,
p2q3, etc., represent the total utilities of successive bottles of ink; while the equal spaces
o r1,
p1r2, etc., represent the total utilities of successive shillings, which we may assume to be
practically invariable. There is no doubt that three bottles will be purchased, but the fourth will not be purchased unless the mixtilinear figure
p3q3q4p4 exceed in area the rectangle
p3r3r4p4.
Cases of this kind are similar to those treated in pp. 120-124, where the things exchanged are indivisible, except that the question of exchange or no exchange occurs over and over again with respect to each successive unit, and is decided in respect to each by the excess of the total utility of the unit to be received over the total utility of that to be given. There is indeed perfect harmony between the cases where equations can and where they cannot be established; for we have only to imagine the indivisible units of commodity to be indefinitely lessened in size to enable us to pass gradually down to the case where equality of the increments of utility is ultimately established.
Negative and Zero Value.
Only a few economists, notably Mr. H. D. Macleod in several of his publications, have noticed the fact that there may be such a thing as negative value. Yet there cannot be the least doubt that people often labour, or pay money to other labourers, in order to get rid of things, and they would not do this unless such things were hurtful, that is, had the opposite quality to utility—disutility. Water, when it gets into a mine, is a costly thing to get out again, and many people have been ruined by wet mines. Quarries and mines usually produce great quantities of valueless rock or earth, variously called duff, spoil, waste, rubbish, and no inconsiderable part of the cost of working arises from the need of raising and carrying this profitless mass of matter and then finding land on which to deposit it. Every furnace yields cinders, dross, or slag, which can seldom be sold for any money, and every household is at the expense of getting rid, in one way or another, of sewage, ashes, swill, and other
rejectanea. Reflection soon shows, in short, that no inconsiderable part of the values with which we deal in practical economics must be
negative values.
It will hardly be needful to show at full length that this negative value may be regarded as varying continuously in the same way as positive value. If after a long drought rain begins to fall heavily, it is
at first hailed as a great benefit; the rain-water may be so valuable as to produce a crop, when otherwise successful agriculture would have been impossible. Rain may thus avert famine; but after the rain has fallen for a certain length of time, the farmer begins to think he has had enough of it; more rain will retard his operations, or injure the growing plants. As the rain continues to fall he fears further injury; water begins to flood his land, and there is even danger of the soil and crops being all washed away together. But the rain unfortunately pours down more and more heavily, until at length perhaps the crops, soil, house, stock,—nay, the farmer himself, are all swept bodily away. That same water, then, which in moderate quantity would have been of the greatest possible benefit, has only to be supplied in greater and greater quantities to become injurious, until it ends with occasioning the ruin, and even the death, of the individual. Those acquainted with the floods and droughts of Australia know that this is no fancy sketch.
*79
In many other cases it might be shown similarly that matter, we can hardly call it commodity, acquires a higher and higher degree of
disutility the greater the quantity which has to be disposed of. Such is the case with the sewage of great towns, the foul or poisoned water from mines, dye-works, etc. Any
obstacle, however, may be regarded as so much discommodity, whether it be a mountain which has to be bored through to make a railway, or a hollow which has to be filled up with an expensive embankment. If a building site requires a certain expenditure in levelling and draining before it can be made use of, the cost of this work is, of course, subtracted from the value which the land would otherwise possess. As every advantage in property gives rise to value, so every disadvantage must be set against that value.
We now come to the question how negative value is to be represented in our equations. Let us suppose a person possessing
a of some commodity to find it insufficient: then it has positive degree of utility for him, that is to say
f(
a) is positive. Suppose
x to be added to
a and gradually increased:
f(
a +
x) will gradually decrease. Let us assume that for a certain value of
x it becomes zero; then, if the further increase of
x turns utility into disutility,
f(
a +
x) will become a negative quantity. How will this negative sign affect the validity of the equations which we have been employing in preceding pages, and in which each member has appeared to be both formally and intrinsically positive? It is plain that we cannot equate a positive to a negative quantity; but it will be found that if, at the same time that we introduce negative utility, we also assign to each increment of commodity the positive or negative sign, according as it is added to or subtracted from the exchanger’s
possessions, that is to say, received or given in exchange, no such difficulty arises.
Suppose A and B respectively to hold
a and
b, and to exchange
dx and
dy of the commodities X and Y. Then it will be apparent from the general character of the argument on pp. 98-100, that the fundamental equation there adopted will be included in the more general form—
a±
x).
dx +
y (
b±
y).
dy = 0.
In this equation either factor of either term may be intrinsically negative, while the alternative signs before
x and
y allow for every possible case of giving and receiving in exchange.
Four possible cases will arise. In the first case, both commodities have utility for each person, that is to say,
f and
y are both positive functions; but A gives some of X in return for some of Y. This means that
dx is negative, and
dy positive, while the quantities in possession after exchange are
a –
x, and
b+
y. Thus the equation becomes
f (
a –
x).
dx +
y (
b+
y).
dy = 0.
We should have merely to transpose the negative term to the other side of the equation, and to assume
b = 0, to obtain the equation on p. 99.
As the second case, suppose that Y possesses disutility for A, so that the function
y becomes for him negative; in order to get rid of
y, he must also pay
x with it, and both these quantities as well as
dy and
dx receive the negative sign. Then the equation takes the shape
a–
x) × (-
dx) –
y (
b–
y) × (-
dy) = 0,
or
f(
a–
x).
dx +
y(
b–
y).
dy = 0.
The third case is the counterpart of the last, and represents B’s position, who receives both
x and
y, on the ground that one of these quantities is
discommodity to him. But putting the matter as the case of A, we may assume
f to be positive,
y negative, and giving the positive sign to all of
x,y,dx, and
dy, we obtain the equation—
a +
x).
dx –
y (
b+
y).
dx = 0.
It is possible to conceive yet a fourth case in which people should be exchanging two discommodities; that is to say, getting rid of one hurtful substance by accepting in place of it what is felt to be less hurtful, though still possessing disutility. In this case we have both
f and
y negative, as well as one of the quantities exchanged; taking
x and
dx as positive, and
y and
dy as negative, the equation assumes the form
f (
a +
x).
dx –
y (
b–
y). (-
dy) = 0,
or
f(
a+
x).
dx +
y(
b–
y).
dy = 0.
It might be difficult to discover any distinct cases of this last kind of exchange. Generally speaking, when a person receives assistance in getting rid of some inconvenient possession, he pays in money or
other commodity for the service of him who helps to remove the burden. It must naturally be a very rare case that the remover has some burden which it would suit the other party to receive in exchange. Yet the contingency may, and no doubt does, sometimes occur. Two adjacent landowners, for instance. might reasonably agree that, if A allows B to throw the spoil of his mine on A’s land, then A shall be allowed to drain his mine into B’s mine. It might happen that B was comparatively more embarrassed by the great quantity of his spoil than by water, and that A had room for the spoil, but could not get rid of the water in other ways without great difficulty. An exchange of inconveniences would then be plainly beneficial.
Looking at the equations obtained in the four cases as stated above, it is apparent that the general equation of exchange consists in equating to zero the sum of one positive and one negative term, so that the signs, both of the utility functions and of the increments, may be disregarded. Thus the fundamental equation may be written in the general form
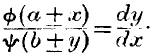
We may express the result of this theory in general terms by saying that the algebraic sum of the utility or disutility received or parted with, as regards the last increments concerned in an act of traffic, will always be zero. It also follows that, without regard to sign, the increments are in magnitude inversely
as their degrees of utility or disutility. The reader will not fail to notice the remarkable analogy between this theory and that of the equilibrium of two forces regarded according to the principle of virtual velocities. A rigid lever will remain in equilibrium under the action of two forces, provided that the algebraic sum of the forces, each multiplied by its infinitely small displacement, be zero. Substitute for force degree of utility, positive or negative, and for infinitely small displacements infinitely small quantities of commodity exchanged, and the principles are identical.
It still remains to consider the imaginary case in which substances possess or are supposed to possess neither utility nor disutility, and are yet exchanged in finite quantities. Substituting the ratio of
y and
x for that of
dy and
dx, the general equation
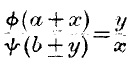
will give the value
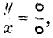
both the functions of utility being zero. This means that the quantities exchanged will be indeterminate so far as the theory of utility goes. If one substance possesses utility, and the other does not, the ratio of exchange becomes either
y/0 or 0/
y, infinity or zero, indicating that there can be no comparison in our theory between things which do and those which do not possess utility. Practically speaking, such cases do not occur except in an approximate manner. Such things as cinders, shavings, night
soil, etc., have either low degrees of utility or disutility. If the dustman takes them away for nothing, they must have utility for him sufficient to pay the cost of removal. When the dust is riddled, one part is usually found to have utility just sufficient to balance the disutility of the remainder, giving us an instance of the second or third form of the equation of exchange according as we regard the matter from the householder’s or the dustman’s point of view.
Equivalence of Commodities.
Much confusion is thrown into the statistical investigation of questions of supply and demand by the circumstance that one commodity can often replace another, and serve the same purposes more or less perfectly. The same, or nearly the same, substance is often obtained from two or three sources. The constituents of wheat, barley, oats, and rye are closely similar, if not identical. Vegetable structures are composed mainly of the same chemical compound in nearly all cases. Animal meat, again, is of nearly the same composition from whatever animal derived. There are endless differences of flavour and quality, but these are often insufficient to prevent one kind from serving in place of another.
Whenever different commodities are thus applicable to the same purposes, their conditions of demand and exchange are not independent. Their mutual ratio of exchange cannot vary much, for it will be
closely defined by the ratio of their utilities. Beef and mutton, for instance, differ so slightly, that people eat them almost indifferently. But the whole-sale price of mutton, on an average, exceeds that of beef in the ratio of 9 to 8, and we must therefore conclude that people generally esteem mutton more than beef in this proportion, otherwise they would not buy the dearer meat. It follows that the final degrees of utility of these meats are in this ratio, or that if
fx be the degree of utility of mutton, and
yy that of beef, we have
fx = 9.
yy.
This equation would doubtless not hold true in extreme circumstances; if mutton became comparatively scarce, there would probably be some persons willing to pay a higher price, merely because it would then be considered a delicacy. But this is certain, that, so long as the equation of utilities holds true, the ratio of exchange between mutton and beef will not diverge from that of 8 to 9. If the supply of beef falls off to a small extent, people will not pay a higher price for it, but will eat more mutton; and if the supply of mutton falls off, they will eat more beef. The conditions of supply will have no effect upon the ratio of exchange; we must, in fact, treat beef and mutton as one commodity of two different strengths, just as gold at eighteen and gold at twenty carats are hardly considered as two but rather as one commodity, of which twenty parts of one are equivalent to eighteen of the other.
It is upon this principle that we must explain, in harmony with Cairnes’ views, the extraordinary permanence of the ratio of exchange of gold and silver, which from the commencement of the eighteenth century up to recent years never diverged much from 15 to 1. That this fixedness of ratio did not depend entirely upon the amount or cost of production is proved by the very slight effect of the Australian and Californian gold discoveries, which never raised the gold price of silver more than about 4 2/3 per cent, and failed to have a permanent effect of more than 1½ per cent. This permanence of relative values may have been partially due to the fact, that gold and silver can be employed for exactly the same purposes, but that the superior brilliancy of gold occasions it to be preferred, unless it be about 15 or 15½ times as costly as silver. Much more probably, however, the explanation of the fact is to be found in the fixed ratio of 15½ to 1, according to which these metals are exchanged in the currency of France and some other continental countries. The French Currency Law of the Year XI. established an artificial equation—
Utility of gold = 15½ × Utility of silver;
and it is probably not without some reason that Wolowski and other recent French economists attributed to this law of replacement an important effect in preventing disturbance in the relations of gold and silver.
Since the first edition of this work was published, the views of Wolowski have received striking verification
in the unprecedented fall in the value of silver which has occurred in the last three or four years. The ratio of equivalent weights of silver and gold, which had never before risen much above 16 to 1, commenced to rise in 1874, and was at one time (July 1876) as high as 22·5 to 1 in the London market. Though it has since fallen, the ratio continues to be subject to frequent considerable oscillations. The great production of silver in Nevada may contribute somewhat to this extraordinary result, but the principal cause must be the suspension of the French Law of the Double Standard, and the demonetisation of silver in Germany, Scandinavia, and elsewhere. As I have treated the subject of the value of silver and the Double Standard elsewhere,
*80 I need not pursue it here.
Acquired Utility of Commodities.
The Theory of Exchange, as explained above, rests entirely on the consideration of quantities of utility, and no reference to labour or cost of production has been made. The
value of a divisible commodity, if I may for a moment use the dangerous
term, is measured, not, indeed, by its total utility, but by its final degree of utility, that is by the intensity of the need we have for
more of it. But the power of exchanging one commodity for another greatly extends the range of utility. We are no longer limited to considering the degree of utility of a commodity as regards the wants of its immediate possessor; for it may have a higher usefulness to some other person, and can be transferred to that person in exchange for some commodity of a higher degree of utility to the purchaser. The general result of exchange is, that all commodities sink, as it were, to the same level of utility in respect of the last portions consumed.
In the Theory of Exchange we find that the possessor of any divisible commodity will exchange such a portion of it, that the next increment would have exactly equal utility with the increment of other produce which he would receive for it. This will hold good however various may be the kinds of commodity he requires. Suppose that a person possesses one single kind of commodity, which we may consider to be money, or income, and that
p,q,r,s,t, etc., are quantities of other commodities which he purchases with portions of his income. Let
x be the uncertain quantity of money which he will desire not to exchange; what relation will exist between these quantities
x,p,q,r, etc.? This relation will partly depend upon the ratio of exchange, partly on the final degree of utility of these commodities. Let us
assume, for a moment, that all the ratios of exchange are equalities, or that a unit of one is always to be purchased with a unit of another. Then, plainly, we must have the degrees of utility equal, otherwise there would be advantage in acquiring more of that possessing the higher degree of utility. Let the sign
f denote the function of utility, which will be different in each case; then we have simply the equations—
f2p =
f3q =
f4r =
f5s = etc.
But, as a matter of fact, the ratio of exchange is seldom or never that of unit for unit; and when the quantities exchanged are unequal, the degrees of utility will not be equal. If for one pound of silk I can have three of cotton, then the degree of utility of cotton must be a third that of silk, otherwise I should gain by exchange. Thus the general result of the facility of exchange prevailing in a civilised country is, that
a person procures such quantities of commodities that the final degrees of utility of any pair of commodities are inversely as the ratios of exchange of the commodities.
Let
x1,
x2,
x3,
x4, etc., be the portions of his income given for
p,q,r,s, etc., respectively, then we must have
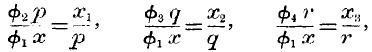
and so on. The theory thus represents the fact, that a person distributes his income in such a way as to equalise the utility of the final increments of all commodities consumed. As water runs into hollows until
it fills them up to the same level, so wealth runs into all the branches of expenditure. This distribution will vary greatly with different individuals, but it is self-evident that the want which an individual feels most acutely at the moment will be that upon which he will expend the next increment of his income. It obviously follows that
in expending a person’s income to the greatest advantage, the algebraic sum of the quantities of commodity received or parted with, each multiplied by its final degree of utility, will be zero.
We can now conceive, in an accurate manner, the utility of money, or of that supply of commodity which forms a person’s income. Its final degree of utility is measured by that of any of the other commodities which he consumes. What, for instance, is the utility of one penny to a poor family earning fifty pounds a year? As a penny is an inconsiderable portion of their income, it may represent one of the infinitely small increments, and its utility is equal to the utility of the quantity of bread, tea, sugar, or other articles which they could purchase with it, this utility depending upon the extent to which they were already provided with those articles. To a family possessing one thousand pounds a year, the utility of a penny may be measured in an exactly similar manner; but it will be much less, because their want of any given commodity will be satiated or satisfied to a much greater extent, so that the urgency of need for a pennyworth more of any article is much reduced.
The general result of exchange is thus to produce a certain equality of utility between different commodities, as regards the same individual; but between different individuals no such equality will tend to be produced. In Economics we regard only commercial transactions, and no equalisation of wealth from charitable motives is considered. The degree of utility of wealth to a very rich man will be governed by its degree of utility in that branch of expenditure in which he continues to feel the most need of further possessions. His primary wants will long since have been fully satisfied; he could find food, if requisite, for a thousand persons, and so, of course, he will have supplied himself with as much as he in the least desires. But so far as is consistent with the inequality of wealth in every community, all commodities are distributed by exchange so as to produce the maximum of benefit. Every person whose wish for a certain thing exceeds his wish for other things, acquires what he wants provided he can make a sufficient sacrifice in other respects. No one is ever required to give what he more desires for what he less desires, so that perfect freedom of exchange must be to the advantage of all.
The Gain by Exchange.
It is a most important result of this theory that the ratio of exchange gives no indication of the real benefit derived from the action of exchange. So
many trades are occupied in buying and selling, and make their profits by buying low and selling high, that there arises a fallacious tendency to believe that the whole benefit of trade depends upon the differences of prices. It is implied that to pay a high price is worse than doing without the article, and the whole financial system of a great nation may be distorted in the effort to carry out a false theory.
This is the result to which some of J. S. Mill’s remarks, in his
Theory of International Trade, would lead. That theory is always ingenious, and as it seems to me, nearly always true; but he draws from it the following conclusion:
*81—”The countries which carry on their foreign trade on the most advantageous terms are those whose commodities are most in demand by foreign countries, and which have themselves the least demand for foreign commodities. From which, among other consequences, it follows that the richest countries,
cœteris paribus, gain the least by a given amount of foreign commerce: since, having a greater demand for commodities generally, they are likely to have a greater demand for foreign commodities, and thus modify the terms of interchange to their own disadvantage. Their aggregate gains by foreign trade, doubtless, are generally greater than those of poorer countries, since they carry on a greater amount of such trade, and gain the benefit of cheapness on a larger consumption: but
their gain is less on each individual article consumed.”
In the absence of any explanation to the contrary, this passage must be taken to mean that the advantage of foreign trade depends upon the terms of exchange, and that international trade is less advantageous to a rich than to a poor country. But such a conclusion involves confusion between two distinct things—the price of a commodity and its total utility. A country is not merely like a great mercantile firm buying and selling goods, and making a profit out of the difference of price; it buys goods in order to consume them. But, in estimating the benefit which a consumer derives from a commodity, it is the total utility which must be taken as the measure, not the final degree of utility on which the terms of exchange depend.
 To illustrate this truth we may employ the curves in Fig. VII. to represent the functions of utility of two commodities. Let the wool of Australia be represented by the line
To illustrate this truth we may employ the curves in Fig. VII. to represent the functions of utility of two commodities. Let the wool of Australia be represented by the line
ob, and its total utility to Australia by the area of the curvilinear figure
obrp. Let the utility of a second commodity, say cotton goods, to Australia be similarly represented in the lower curve, so that the quantity of commodity measured by
o‘
b‘ gives a total utility represented by the figure
o‘
p‘
r‘
b‘. Then, if Australia gives half its wool,
ab, for the quantity of cotton goods represented by
o‘
a‘, it loses the utility
aqrb, but gains that represented by the larger area
o‘
p‘
q‘
a‘. There is
accordingly a considerable net gain of utility, which is the real object of exchange. Even had Australia sold its wool at a lower price, obtaining cotton goods only to the amount of
o‘
c, the utility of this amount,
op‘
sc, would have exceeded that of the wool given for it.
So far is Mill’s statement from being fundamentally correct, that I believe the truth lies in the opposite direction. As a general rule, the greatness of the price which a country is willing and able to pay for the productions of other countries, measures, or at least manifests, the greatness of the benefit which it derives from such imports. He who pays a high price must either have a very great need of that
which he buys, or very little need of that which he pays for it; on either supposition there is gain by exchange. In questions of this sort there is but one rule which can be safely laid down, namely, that no one will buy a thing unless he expects advantage from the purchase; and perfect freedom of exchange, therefore, tends to the maximising of utility.
One advantage of the Theory of Economics, carefully studied, will be to make us very careful in our conclusions when the matter is not of the simplest possible nature. The fact that we can most imperfectly estimate the total utility of any one commodity should prevent us, for instance, from attempting to measure the benefit of any trade. Accordingly, when Mill proceeds from his theory of international trade to that of taxation, and arrives at the conclusion that one nation may, by means of taxes on commodities imported, “appropriate to itself, at the expense of foreigners, a larger share than would otherwise belong to it of the increase in the general productiveness of the labour and capital of the world,”
*82 I venture to question the truth of his results. I conceive that his arguments involve a confusion between the ratio of exchange and the total utility of a commodity, and a far more accurate knowledge of economical laws than any one yet possesses would be required to estimate the true effect of a tax. Customs duties may be requisite as a means of raising revenue, but the time is past when any economist should give the slightest
countenance to their employment for manipulating trade, or for interfering with the natural tendency of exchange to increase utility.
Numerical Determination of the Laws of Utility.
The future progress of Economics as a strict science must greatly depend upon our acquiring more accurate notions of the variable quantities concerned in the theory. We cannot really tell the effect of any change in trade or manufacture until we can with some approach to truth express the laws of the variation of utility numerically. To do this we need accurate statistics of the quantities of commodities purchased by the whole population at various prices. The price of a commodity is the only test we have of the utility of the commodity to the purchaser; and if we could tell exactly how much people reduce their consumption of each important article when the price rises, we could determine, at least approximately, the variation of the final degree of utility—the all-important element in Economics.
In such calculations we may at first make use of the simpler equation given on p. 113. For the first approximation we may assume that the general utility of a person’s income is not affected by the changes of price of the commodity; so that, if in the equation
m.yc
we may have many different corresponding values for
x and
m, we may treat
yc, the utility of money, as
a constant, and determine the general character of the function
fx, the final degree of utility. This function would doubtless be a purely empirical one—a mere aggregate of terms devised so that their sum shall vary in accordance with statistical facts. The subject is too complex to allow of our expecting any simple precise law like that of gravity. Nor, when we have got the laws, shall we be able to give any exact explanation of them. They will be of the same character as the empirical formulæ used in many of the physical sciences—mere aggregates of mathematical symbols intended to replace a tabular statement.
*83 Nevertheless, their determination will render Economics a science as exact as many of the physical sciences; as exact, for instance, as Meteorology is likely to be for a very long time to come.
The method of determining the function of utility explained above will hardly apply, however, to the main elements of expenditure. The price of bread, for instance, cannot be properly brought under the equation in question, because, when the price of bread rises much, the resources of poor persons are strained, money becomes scarcer with them, and
yc, the utility of money, rises. The natural result is, the lessening of expenditure in other directions; that is to say, all the wants of a poor person are supplied to a less degree of satisfaction when food is dear than when it is cheap. When in the long course of scientific
progress a sufficient supply of suitable statistics has been at length obtained, it will become a mathematical problem of no great difficulty how to disentangle the functions expressing the degrees of utility of various commodities. One of the first steps, no doubt, will be to ascertain what proportion of the expenditure of poor people goes to provide food, at various prices of that food. But great difficulty is thrown in the way of all such inquiries by the vast differences in the condition of persons; and still greater difficulties are created by the complicated ways in which one commodity replaces or serves instead of another.
Opinions as to the Variation of Price.
There is no difficulty in finding in works of Economists remarks upon the relation between a change in the supply of a commodity and the consequent rise of price. The general principles of the variation of utility have been familiar to many writers.
As a general rule the variation of price is much more marked in the case of necessaries of life than in the case of luxuries. This result would follow from the fact observed by Adam Smith, that “The desire for food is limited in every man by the narrow capacity of the human stomach; but the desire of the conveniences and ornaments of building, dress, equipage, and household furniture, seems to have no limit or certain boundary.” As I assert that value depends upon desire for more, it follows that any
excessive supply of food will lower its price very much more than in the case of articles of luxury. Reciprocally, a deficiency of food will raise its price much more than would happen in the case of less necessary articles. This conclusion is in harmony with facts; for Chalmers says:
*84 “The necessaries of life are far more powerfully affected in the price of them by a variation in their quantity than are the luxuries of life. Let the crop of grain be deficient by one-third in its usual amount, or rather, let the supply of grain in the market, whether from the home produce or by importation, be curtailed to the same extent, and this will create a much greater addition than of one-third to the price of it. It is not an unlikely prediction that its cost would be more than doubled by the shortcoming of one-third or one-fourth in the supply.”
He goes on to explain, at considerable length, that the same would not happen with such an article as rum. A deficiency in the supply of rum from the West Indies would occasion a rise of price, but not to any great extent, because there would be a substitution of other kinds of spirits, or else a reduction in the amount consumed. Men can live without luxuries, but not without necessaries. “A failure in the general supply of esculents to the extent of one-half would more than quadruple the price of the first necessaries of life, and would fall with very aggravated pressure
on the lower orders. A failure to the same extent in all the vineyards of the world would most assuredly not raise the price of wine to anything near this proportion. Rather than pay four times the wonted price for Burgundy, there would be a general descent to claret, or from that to port, or from that to the home-made wines of our own country, or from that to its spirituous, or from that to its fermented liquors.”
*85 He points to sugar especially as an article which would be extensively thrown out of consumption by any great rise in price,
*86 because it is a luxury, and at the same time forms a considerable element in expenditure. But he thinks that, if an article occasions a total expenditure of very small amount, variations of price will not much affect its consumption.
Speaking of nutmeg, he says: “There is not sixpence a year consumed of it for each family in Great Britain; and perhaps not one family that spends more than a guinea on this article alone. Let the price then be doubled or trebled; this will have no perceptible effect on the demand; and the price will far rather be paid than that the wonted indulgence should in any degree be foregone…. The same holds true of cloves, and cinnamon, and Cayenne pepper, and all the precious spiceries of the East; and it is thus that while, in the general, the price of necessaries differs so widely from that of luxuries, in regard to the extent of oscillation, there is a remarkable
approximation in this matter between the very commonest of these necessaries and the very rarest of these luxuries.”
*87
In these interesting observations Chalmers correctly distinguishes between the effect of desire for the commodity in question and that for other çommodities. The cost of nutmeg does not appreciably affect the general expenditure on other things, and the equation on p. 113 therefore applies. But if sugar becomes scarce, to consume as before would necessitate a reduction of consumption in other directions; and as the degree of utility of more necessary articles rises much more rapidly than that of sugar, it is the latter article which is thrown out of use by preference. This is a far more complex case, which includes also the case of corn and all large articles of consumption.
Chalmers’ remarks on the price of sugar are strongly supported by facts concerning the course of the sugar markets in 1855-6. In the year 1855, as is stated in Tooke’s
History of Prices,*88 attention was suddenly drawn to a considerable reduction which had taken place in the stocks of sugar. The price rapidly advanced, but before it had reached the highest point the demand became almost wholly suspended. Not only did retail dealers avoid replenishing their stocks, but there was an immediate and sometimes entire cessation of consumption among extensive classes. There were instances among the
retail grocers of their not selling a single pound of sugar until prices receded to what the public was satisfied was a reasonable rate.
Variation of the Price of Corn.
As to Chalmers’ ingenious remarks upon the consumption of nutmeg, he seems to be at least partially correct. To a certain extent he brings into view the principle explained above, that when only a small quantity of income is required to purchase a certain kind of commodity in sufficient abundance, the degree of utility of income will not be appreciably affected by the price paid, that is to say (p. 113)
yc remains approximately constant. It follows that
fx/
m is constant, or in other words the final degree of utility of the small commodity purchased must be directly proportional to the price. If then the price rise much, either the consumer must relinquish the use of that commodity almost entirely, or else he must feel such need of it, that a small decrease of consumption is irksome to him; that is to say, looking to our curves of utility, either we must recede to a part of the curve very close to the axis of
y, or else the curve must be one which rises rapidly as we move towards the origin. Now Chalmers assumes that with nutmeg the latter is the case. People accustomed to use it in his time were so fond of it that they would pay a much higher price rather than decrease their consumption considerably.
This means that it possessed a high degree of utility to them, which could only be overbalanced by some serious increase in the value of
yc, which would ultimately mean the need of the necessaries of life.
It is very curious that in this subject, which reaches to the very foundations of Political Economy, we owe more to early than later writers. Before our science could be said to exist at all, writers on Political Arithmetic had got about as far as we have got at present. In a pamphlet of 1737,
*89 it is remarked that “People who understand trade will readily agree with me, that the tenth part of a commodity in a market, more than there is a brisk demand for, is apt to lower the market, perhaps, twenty or thirty per cent, and that a deficiency of a tenth part will cause as exorbitant an advance.” Sir J. Dalrymple,
*90 again, says: “Merchants observe, that if the commodity in market is diminished one-third beneath its mean quantity, it will be nearly doubled in value; and that if it is augmented one-third above its mean quantity, it will sink near one-half in its value; or that, by further diminishing or augmenting the quantity, these disproportions between the quantity and prices vastly increase.” These remarks bear little signs of accuracy, indeed, for the writers have spoken of commodities in general as if they all varied in price in a similar degree. It is probable that they were thinking of
corn or other kinds of the more necessary food. In the
Spectator we find a conjecture,
*91 that the production of one-tenth part more of grain than is usually consumed would diminish the value of the grain one-half. I know nothing more strange and discreditable to statists and economists than that in so important a point as the relations of price and supply of the main article of food, we owe our most accurate estimates to writers who lived from one to two centuries ago.
There is a celebrated estimate of the variation of the price of corn which I have found quoted in innumerable works on Economics. It is commonly attributed to Gregory King, whose name should be held in honour as one of the fathers of statistical science in England. Born at Lichfield in 1648, King devoted himself much to mathematical studies, and was often occupied in surveying. His principal public appointments were those of Lancaster Herald and Secretary to the Commissioners of Public Accounts; but he is known to fame by the remarkable statistical tables concerning the population and trade of England, which he completed in the year 1696. His treatise was entitled
Natural and Political Observations and Conclusions upon the State and Condition of England, 1696. It was never printed in the author’s lifetime, but the contents were communicated in a most liberal manner to Dr. Davenant, who, making suitable acknowledgments as to the source of his information, founded thereupon his
Essay upon the Probable
Methods of making a People gainers in the Balance of Trade.*92 Our knowledge of Gregory King’s conclusions was derived from this and other essays of Davenant, until George Chalmers printed the whole treatise at the end of the third edition of his well-known
Estimate of the Comparative Strength of Great Britain.
The estimate of which I am about to speak is given by Davenant in the following words:
*93 “We take it, that a defect in the harvest may raise the price of corn in the following proportions:—
So that when corn rises to treble the common rate, it may be presumed that we want above 1/3 of the common produce; and if we should want 5/10, or half the common produce, the price would rise to near five times the common rate.”
Though this estimate has always been attributed to Gregory King, I cannot find it in his published treatise; nor does Davenant, who elsewhere makes full acknowledgments of what he owes to King, here attribute it to his friend. It is therefore, perhaps, due to Davenant.
We may re-state this estimate in the following manner, taking the average harvest and the average price of corn as unity:—
| Quantity of Corn | 1.0 | .9 | .8 | .7 | .6 | .5 |
| Price | 1.0 | 1.3 | 1.8 | 2.6 | 3.8 | 5.5 |
Many writers have commented on this estimate. Thornton
*94 observes that it is probably exceedingly inaccurate, and that it is not clear whether the total stock, or only the harvest of a single year, is to be taken as deficient. Tooke,
*95 however, than whom on such a point there is no higher authority, believes that King’s estimate “is not very wide of the truth, judging from the repeated occurrence of the fact that the price of corn in this country has risen from one hundred to two hundred per cent and upwards when the utmost computed deficiency of the crops has not been more than between one-sixth and one-third of an average.”
I have endeavoured to ascertain the law to which Davenant’s figures conform, and the mathematical function obtained does not greatly differ from what we might have expected. It is probable that the price of corn should never sink to zero, as, if abundant, it could be used for feeding horses, poultry, and cattle, or for other purposes for which it is too costly at present. It is said that in America corn, no doubt Indian corn, has been occasionally used as fuel. On
the other hand, when the quantity is much diminished, the price should rise rapidly, and should become infinite before the quantity is zero, because famine would then be impending. The substitution of potatoes and other kinds of food renders the famine point very uncertain; but I think that a total deficiency of corn could not be made up by other food. Now a function of the form
fulfils these conditions; for it becomes infinite when
x is reduced to
b, but for greater values of
x always decreases as
x increases. An inspection of the numerical data shows that
n is about equal to 2, and, assuming it to be exactly 2, I find that the most probable values of
a and
b are
a = .824 and
b = .12. The formula thus becomes
The following numbers show the degree of approximation between the first of these formulæ and the data of Davenant:—
| Harvest | 1.0 | .9 | .8 | .7 | .6 | .5 |
| Price (Davenant) | 1.0 | 1.3 | 1.8 | 2.6 | 3.8 | 5.5 |
| Price calculated | 1.06 | 1.36 | 1.78 | 2.45 | 3.58 | 5.71 |
I cannot undertake to say how nearly Davenant’s estimate agrees with experience; but, considering the close approximation in the above numbers, we may safely substitute the empirical formula for his numbers; and there are other reasons already stated for
supposing that this formula is not far from the truth. Roughly speaking, the price of corn may be said to vary inversely as the square of the supply, provided that this supply be not unusually small. I find that this is nearly the same conclusion as Whewell drew from the same numbers. He says:
*96 “If the above numbers were to be made the basis of a mathematical rule, it would be found that the price varies inversely as the square of the supply, or rather in a higher ratio.”
There is further reason for believing that the price of corn varies more rapidly than in the inverse ratio of the quantity. Tooke estimates
*97 that in 1795 and 1796 the farmers of England gained seven millions sterling in each year by a deficiency of one-eighth part in the wheat crop, not including the considerable profit on the rise of price of other agricultural produce. In each of the years 1799 and 1800, again, farmers probably gained eleven millions sterling by deficiency. If the price of wheat varied in the simple inverse proportion of the quantity, they would neither gain nor lose, and the fact that they gained considerably agrees with our formula as given above.
The variation of utility has not been overlooked by mathematicians, who had observed, as long ago as the early part of last century—before, in fact, there was any science of Political Economy at all—that
the theory of probabilities could not be applied to commerce or gaming without taking notice of the very different utility of the same sum of money to different persons. Suppose that an even and fair bet is made between two persons, one of whom has £10,000 a year, the other £100 a year; let it be an equal chance whether they gain or lose £50. The rich person will, in neither case, feel much difference; but the poor person will receive far more harm by losing £50 than he can be benefited by gaining it. The utility of money to a poor person varies rapidly with the amount; to a rich person less so. Daniel Bernoulli, accordingly, distinguished in any question of probabilities between the
moral expectation and the
mathematical expectation, the latter being the simple chance of obtaining some possession, the former the chance as measured by its utility to the person. Having no means of ascertaining numerically the variation of utility, Bernoulli had to make assumptions of an arbitrary kind, and was then able to obtain reasonable answers to many important questions. It is almost self-evident that the utility of money decreases as a person’s total wealth increases; if this be granted, it follows at once that gaming is, in the long run, a sure way to lose utility; that every person should, when possible, divide risks, that is, prefer two equal chances of £50 to one similar chance of £100; and the advantage of insurance of all kinds is proved from the same theory. Laplace drew a similar distinction between the
fortune physique, or the actual amount of a person’s income, and the
fortune morale, or its benefit to him.”
*98
In answer to the objections of an ingenious correspondent, it may be remarked that when we say gaming is a sure way to lose utility, we take no account of the utility—that is, the pleasure attaching to the pursuit of gaming itself; we regard only the commercial loss or gain. If a person with a certain income prefers to run the risk of losing a portion of it at play, rather than spending it in any other way, it must no doubt be conceded that the political economist, as such, can make no conclusive objection. If the gamester is so devoid of other tastes that to spend money over the gaming-table is the best use he can discover for it, economically speaking, there is nothing further to be said. The question then becomes a moral, legislative, or political one. A source of amusement which, like gaming, betting, dram-drinking, or opium-eating, is not in itself always pernicious, may come to be regarded as immoral, if in a considerable proportion of cases it leads to excessive and disastrous results. But this question evidently leads us into a class of subjects which could not be appropriately discussed in this work treating of pure economic theory.
The Origin of Value.
The preceding pages contain, if I am not mistaken, an explanation of the nature of value which will, for the most part, harmonise with previous views upon the subject. Ricardo has stated, like most other economists, that utility is absolutely essential to value; but that “possessing utility, commodities derive their exchangeable value from two sources: from their scarcity, and from the quantity of labour required to obtain them.”
*99 Senior, again, has admirably defined wealth, or objects possessing value, as “those things, and those things only, which are transferable, are limited in supply, and are directly or indirectly productive of pleasure or preventive of pain.” Speaking only of things which are transferable, or capable of being passed from hand to hand, we find that two of the clearest definitions of value recognise
utility and
scarcity as the essential qualities. But the moment that we distinguish between the total utility of a mass of commodity and the degree of utility of different portions, we may say that it is scarcity which prevents the fall in the final degree of utility. Bread has the almost infinite utility of maintaining life, and when it becomes a question of life or death, a small quantity of food exceeds in value all other things. But when we enjoy our ordinary supplies of food, a loaf of bread has little
value, because the utility of an additional loaf is small, our appetites being satiated by our customary meals.
I have pointed out the excessive ambiguity of the word Value, and the apparent impossibility of using it safely. When intended to express the mere fact of certain articles exchanging in a particular ratio, I have proposed to substitute the unequivocal expression—
ratio of exchange. But I am inclined to believe that a ratio is not the meaning which most persons attach to the word Value. There is a certain sense of esteem or desirableness, which we may have with regard to a thing apart from any distinct consciousness of the ratio in which it would exchange for other things. I may suggest that this distinct feeling of value is probably identical with the final degree of utility. While Adam Smith’s often-quoted
value in use is the total utility of a commodity to us, the
value in exchange is defined by the
terminal utility, the remaining desire which we or others have for possessing more.
There remains the question of labour as an element of value. Economists have not been wanting who put forward labour as the
cause of value, asserting that all objects derive their value from the fact that labour has been expended on them; and it is thus implied, if not stated, that value will be proportional to labour. This is a doctrine which cannot stand for a moment, being directly opposed to facts. Ricardo disposes of such an opinion when he says:
*100 “There
are some commodities, the value of which is determined by their scarcity alone. No labour can increase the quantity of such goods, and therefore their value cannot be lowered by an increased supply. Some rare statues and pictures, scarce books and coins, wines of a peculiar quality, which can be made only from grapes grown on a particular soil, of which there is a very limited quantity, are all of this description. Their value is wholly independent of the quantity of labour originally necessary to produce them, and varies with the varying wealth and inclinations of those who are desirous to possess them.”
The mere fact that there are many things, such as rare ancient books, coins, antiquities, etc., which have high values, and which are absolutely incapable of production now, disperses the notion that value depends on labour. Even those things which are producible in any quantity by labour seldom exchange exactly at the corresponding values.
*101 The market price of corn, cotton, iron, and most other things is, in the prevalent theories of value, allowed to fluctuate above or below its natural or cost value. There may, again, be any discrepancy between the quantity of
labour spent upon an object and the value ultimately attaching to it. A great undertaking like the Great Western Railway, or the Thames Tunnel, may embody a vast amount of labour, but its value depends entirely upon the number of persons who find it useful. If no use could be found for the Great Eastern steamship, its value would be
nil, except for the utility of some of its materials. On the other hand, a successful undertaking, which happens to possess great utility, may have a value, for a time at least, far exceeding what has been spent upon it, as in the case of the Atlantic cable. The fact is, that
labour once spent has no influence on the future value of any article: it is gone and lost for ever. In commerce bygones are for ever bygones; and we are always starting clear at each moment, judging the values of things with a view to future utility. Industry is essentially prospective, not retrospective; and seldom does the result of any undertaking exactly coincide with the first intentions of its promoters.
But though labour is never the cause of value, it is in a large proportion of cases the determining circumstance, and in the following way:—
Value depends solely on the final degree of utility. How can we vary this degree of utility?—By having more or less of the commodity to consume. And how shall we get more or less of it?—By spending more or less labour in obtaining a supply. According to this view, then, there are two steps between labour and value. Labour affects supply, and supply affects the degree
of utility, which governs value, or the ratio of exchange. In order that there may be no possible mistake about this all-important series of relations. I will re-state it in a tabular form, as follows:—
Cost of production determines supply.
Supply determines final degree of utility.
Final degree of utility determines value.
But it is easy to go too far in considering labour as the regulator of value; it is equally to be remembered that labour is itself of unequal value. Ricardo, by a violent assumption, founded his theory of value on quantities of labour considered as one uniform thing. He was aware that labour differs infinitely in quality and efficiency, so that each kind is more or less scarce, and is consequently paid at a higher or lower rate of wages. He regarded these differences as disturbing circumstances which would have to be allowed for; but his theory rests on the assumed equality of labour. This theory rests on a wholly different ground. I hold labour to be
essentially variable, so that
its value must be determined by the value of the produce, not the value of the produce by that of the labour. I hold it to be impossible to compare
à priori the productive powers of a navvy, a carpenter, an iron-puddler, a schoolmaster, and a barrister. Accordingly, it will be found that not one of my equations represents a comparison between one man’s labour and another’s. The equation, if there is
one at all, is between the same person in two or more different occupations. The subject is one in which complicated action and reaction takes place, and which we must defer until after we have described, in the next chapter, the Theory of Labour.
Œuvres Complètes de Condillac, 1803, tom. 6
me, p. 20.
market, with admirable brevity and precision, but exactly to the same effect as the text above. He incidentally says in a footnote (
Récherches sur les Principes Mathématiques de la Théorie des Richesses, Paris, 1838, p. 55), “On sait que les économistes entendent par
marché, non pas un lieu déterminé ou se consomment les achats et les ventes, mais tout un territoire dont les parties sont unies par des rapports de libre commerce, en sorte que les prix s’y nivellent avec facilité et promptitude.”
Cyclopœdia of Commerce, ed. 1846, p. 466.
Lessons, sec. 91.
On Labour; its Wrongful Claims and Rightful Dues (1869), p. 58.
Australian Almanack, Sydney, 1859, p. 61. Also Mr. H. C. Russell’s
Climate of New South Wales.
Investigations in Currency and Finance, 1885).
Money and the Mechanism of Exchange (International Scientific Series), chap. xii. This chapter has been translated by M. H. Gravez, and reprinted in the
Bibliothèque Utile, vol. xliv. (Germer Baillière), Paris, 1878. See also Papers on the Silver Question read before the American Social Science Association at Saratoga, September 5, 1877, Boston, 1877, and
Bankers’ Magazine, December 1877 (reprinted in
Investigations in Currency and Finance, 1884).
Principles of Science, chap. xxii., new ed., pp. 487-489, and the references there given.
Christian and Economic Polity of a Nation, vol. ii. p. 240.
Christian and Economic Polity of a Nation, vol. ii. p. 242.
Christian and Economic Polity of a Nation, vol. ii. p. 252.
Inquiry into the Nature and Origin of Public Wealth, 2d ed., 1819, pp. 51, 52.
History of the Theory of Probability, chap. xi., etc.
Recent Political Economy, 8vo, London, 1867, p. 99, states that contracts have been made to manufacture the Enfield Rifle, of identically the same pattern, at prices ranging from 70s. each down to 20s., or even lower. The wages of the workmen varied from 40s. or 50s. down to 15s. a week. Such an instance renders it obvious that it is scarcity which governs value, and that it is the value of the produce which determines the wages of the producers.
Chapter V
