The Theory of Political Economy
By William Stanley Jevons
THE contents of the following pages can hardly meet with ready acceptance among those who regard the Science of Political Economy as having already acquired a nearly perfect form. I believe it is generally supposed that Adam Smith laid the foundations of this science; that Malthus, Anderson, and Senior added important doctrines; that Ricardo systematised the whole; and, finally, that Mr. J. S. Mill filled in the details and completely expounded this branch of knowledge. Mr. Mill appears to have had a similar notion; for he distinctly asserts that there was nothing; in the Laws of Value which remained for himself or any future writer to clear up. Doubtless it is difficult to help feeling that opinions adopted and confirmed by such eminent men have much weight of probability in their favour. Yet, in the other sciences this weight of authority has not been allowed to restrict the free examination of new opinions and theories; and it has often been ultimately proved that authority was on the wrong side.There are many portions of Economical doctrine which appear to me as scientific in form as they are consonant with facts. I would especially mention the Theories of Population and Rent, the latter a theory of a distinctly mathematical character, which seems to give a clue to the correct mode of treating the whole science. Had Mr. Mill contented himself with asserting the unquestionable truth of the Laws of Supply and Demand, I should have agreed with him. As founded upon facts, those laws cannot be shaken by any theory; but it does not therefore follow, that our conception of Value is perfect and final. Other generally accepted doctrines have always appeared to me purely delusive, especially the so-called Wage Fund Theory. This theory pretends to give a solution of the main problem of the science—to determine the wages of labour; yet, on close examination, its conclusion is found to be a mere truism, namely, that the average rate of wages is found by dividing the whole amount appropriated to the payment of wages by the number of those between whom it is divided. Some other supposed conclusions of the science are of a less harmless character, as, for instance, those regarding the advantage of exchange (see the section on “The Gain by Exchange,” p. 141). [From the Preface to the First Edition]
First Pub. Date
1871
Publisher
London: Macmillan and Co.
Pub. Date
1888
Comments
3rd edition. Includes Preface by Harriet Jevons.
Copyright
The text of this edition is in the public domain. Picture of William Stanley Jevons: Photogravure after a photograph of W. Stanley Jevons, taken by Maull & Co., London., courtesy Liberty Fund, Inc.
Definition of Terms.
CHAPTER III
THEORY OF UTILITY
PLEASURE and pain are undoubtedly the ultimate objects of the Calculus of Economics. To satisfy our wants to the utmost with the least effort—to procure the greatest amount of what is desirable at the expense of the least that is undesirable—in other words,
to maximise pleasure, is the problem of Economics. But it is convenient to transfer our attention as soon as possible to the physical objects or actions which are the source to us of pleasures and pains. A very large part of the labour of any community is spent upon the production of the ordinary necessaries and conveniences of life, such as food, clothing, buildings, utensils, furniture, ornaments, etc.; and the aggregate of these things, therefore, is the immediate object of our attention.
It is desirable to introduce at once, and to define, some terms which facilitate the expression of the Principles of Economics. By a
commodity we shall
understand any object, substance, action, or service, which can afford pleasure or ward off pain. The name was originally abstract, and denoted the quality of anything by which it was capable of serving man. Having acquired, by a common process of confusion, a concrete signification, it will be well to retain the word entirely for that signification, and employ the term
utility to denote the abstract quality whereby an object serves our purposes, and becomes entitled to rank as a commodity. Whatever can produce pleasure or prevent pain
may possess utility. J.-B. Say has correctly and briefly defined utility as “la faculté qu’ont les choses de pouvoir servir à l’homme, de quelque manière que ce soit.” The food which prevents the pangs of hunger, the clothes which fend off the cold of winter, possess incontestable utility; but we must beware of restricting the meaning of the word by any moral considerations. Anything which an individual is found to desire and to labour for must be assumed to possess for him utility. In the science of Economics we treat men not as they ought to be, but as they are. Bentham, in establishing the foundations of Moral Science in his great
Introduction to the Principles of Morals and Legislation (page 3), thus comprehensively defines the term in question: “By utility is meant that property in any object, whereby it tends to produce benefit, advantage, pleasure, good, or happiness (all this, in the present case, comes to the same thing), or (what comes again to the same thing) to prevent the happening of mischief,
pain, evil, or unhappiness to the party whose interest is considered.”
This perfectly expresses the meaning of the word in Economics, provided that the will or inclination of the person immediately concerned is taken as the sole criterion, for the time, of what is or is not useful.
The Laws of Human Want.
Economics must be founded upon a full and accurate investigation of the conditions of utility; and, to understand this element, we must necessarily examine the wants and desires of man. We, first of all, need a theory of the consumption of wealth. J. S. Mill, indeed, has given an opinion inconsistent with this. “Political economy,” he says,
*47 “has nothing to do with the consumption of wealth, further than as the consideration of it is inseparable from that of production, or from that of distribution. We know not of any laws of the consumption of wealth, as the subject of a distinct science; they can be no other than the laws of human enjoyment.”
But it is surely obvious that Economics does rest upon the laws of human enjoyment; and that, if those laws are developed by no other science, they must be developed by economists. We labour to produce with the sole object of consuming, and the kinds and amounts of goods produced must be determined with regard to what we want to consume.
Every manufacturer knows and feels how closely he must anticipate the tastes and needs of his customers: his whole success depends upon it; and, in like manner, the theory of Economics must begin with a correct theory of consumption. Many economists have had a clear perception of this truth. Lord Lauderdale distinctly states,
*48 that “the great and important step towards ascertaining the causes of the direction which industry takes in nations… seems to be the discovery of what dictates the proportion of demand for the various articles which are produced.” Senior, in his admirable treatise, has also recognised this truth, and pointed out what he calls the
Law of Variety in human requirements. The necessaries of life are so few and simple, that a man is soon satisfied in regard to these, and desires to extend his range of enjoyment. His first object is to vary his food; but there soon arises the desire of variety and elegance in dress; and to this succeeds the desire to build, to ornament, and to furnish—tastes which, where they exist, are absolutely insatiable, and seem to increase with every improvement in civilisation.
*49
Many French economists also have observed that human wants are the ultimate subject-matter of Economics; Bastiat, for instance, in his
Harmoniesof Political Economy, says,
*50 ”
Wants, Efforts, Satisfaction—this is the circle of Political Economy.”
In still later years, Courcelle-Seneuil actually commenced his treatise with a definition of
want—”Le besoin économique est un désir qui a pour but la possession et la jouissance d’un objet matériel.”
*51 And I conceive that he has given the best possible statement of the problem of Economics when he expresses its object as “à satisfaire nos besoins avec la moindre somme de travail possible.”
*52
Professor Hearn also begins his excellent treatise, entitled
Plutology, or the Theory of Efforts to supply Human Wants, with a chapter in which he considers the nature of the wants impelling man to exertion.
The writer, however, who seems to me to have reached the deepest comprehension of the foundations of Economics is T. E. Banfield. His course of Lectures delivered in the University of Cambridge in 1844, and published under the title of
The Organisation of Labour, is highly interesting, though not always correct. In the following passage
*53 he profoundly points out that the scientific basis of Economics is in a theory of consumption: I need make no excuse for quoting this passage at full length.
“The lower wants man experiences in common
with brutes. The cravings of hunger and thirst, the effects of heat and cold, of drought and damp, he feels with more acuteness than the rest of the animal world. His sufferings are doubtless sharpened by the consciousness that he has no right to be subject to such inflictions. Experience, however, shows that privations of various kinds affect men differently in degree according to the circumstances in which they are placed. For some men the privation of certain enjoyments is intolerable, whose loss is not even felt by others. Some, again, sacrifice all that others hold dear for the gratification of longings and aspirations that are incomprehensible to their neighbours. Upon this complex foundation of low wants and high aspirations the Political Economist has to build the theory of production and consumption.
“An examination of the nature and intensity of man’s wants shows that this connection between them gives to Political Economy its scientific basis. The first proposition of the theory of consumption is, that
the satisfaction of every lower want in the scale creates a desire of a higher character. If the higher desire existed previous to the satisfaction of the primary want, it becomes more intense when the latter is removed. The removal of a primary want commonly awakens the sense of more than one secondary privation: thus a full supply of ordinary food not only excites to delicacy in eating, but awakens attention to clothing. The highest grade in the scale of wants, that of pleasure derived from the
beauties of nature and art, is usually confined to men who are exempted from all the lower privations. Thus the demand for, and the consumption of, objects of refined enjoyment has its lever in the facility with which the primary wants are satisfied. This, therefore, is the key to the true theory of value. Without relative values in the objects to the acquirement of which we direct our power, there would be no foundation for Political Economy as a science.”
Utility is not an Intrinsic Quality.
My principal work now lies in tracing out the exact nature and conditions of utility. It seems strange indeed that economists have not bestowed more minute attention on a subject which doubtless furnishes the true key to the problem of Economics.
In the first place, utility, though a quality of things, is
no inherent quality. It is better described as
a circumstance of things arising out of their relation to man’s requirements. As Senior most accurately says, “Utility denotes no intrinsic quality in the things which we call useful; it merely expresses their relations to the pains and pleasures of mankind.” We can never, therefore, say absolutely that some objects have utility and others have not. The ore lying in the mine, the diamond escaping the eye of the searcher, the wheat lying unreaped, the fruit ungathered for want of consumers, have no utility at all. The most wholesome and necessary kinds of food are useless
unless there are hands to collect and mouths to eat them sooner or later. Nor, when we consider the matter closely, can we say that all portions of the same commodity possess equal utility. Water, for instance, may be roughly described as the most useful of all substances. A quart of water per day has the high utility of saving a person from dying in a most distressing manner. Several gallons a day may possess much utility for such purposes as cooking and washing; but after an adequate supply is secured for these uses, any additional quantity is a matter of comparative indifference. All that we can say, then, is, that water, up to a certain quantity, is indispensable; that further quantities will have various degrees of utility; but that beyond a certain quantity the utility sinks gradually to zero; it may even become negative, that is to say, further supplies of the same substance may become inconvenient and hurtful.
Exactly the same considerations apply more or less clearly to every other article. A pound of bread per day supplied to a person saves him from starvation, and has the highest conceivable utility. A second pound per day has also no slight utility: it keeps him in a state of comparative plenty, though it be not altogether indispensable. A third pound would begin to be superfluous. It is clear, then, that
utility is not proportional to commodity: the very same articles vary in utility according as we already possess more or less of the same article. The like may be said of other things. One suit of clothes per annum is
necessary, a second convenient, a third desirable, a fourth not unacceptable; but we, sooner or later, reach a point at which further supplies are not desired with any perceptible force, unless it be for subsequent use.
Law of the Variation of Utility.
Let us now investigate this subject a little more closely. Utility must be considered as measured by, or even as actually identical with, the addition made to a person’s happiness. It is a convenient name for the aggregate of the favourable balance of feeling produced—the sum of the pleasure created and the pain prevented. We must now carefully discriminate between the
total utility arising from any commodity and the utility attaching to any particular portion of it. Thus the total utility of the food we eat consists in maintaining life, and may be considered as infinitely great; but if we were to subtract a tenth part from what we eat daily, our loss would be but slight. We should certainly not lose a tenth part of the whole utility of food to us. It might be doubtful whether we should suffer any harm at all.
Let us imagine the whole quantity of food which a person consumes on an average during twenty-four hours to be divided into ten equal parts. If his food be reduced by the last part, he will suffer but little; if a second tenth part be deficient, he will feel the want distinctly; the subtraction of the third tenth
part will be decidedly injurious; with every subsequent subtraction of a tenth part his sufferings will be more and more serious, until at length he will be upon the verge of starvation. Now, if we call each of the tenth parts
an increment, the meaning of these facts is, that each increment of food is less necessary, or possesses less utility, than the previous one. To explain this variation of utility we may make use of space-representations, which I have found convenient in illustrating the laws of Economics in my College lectures during fifteen years past.
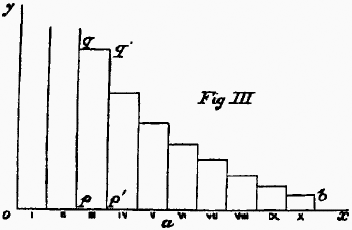 Let the line
Let the line
ox be used as a measure of the quantity of food, and let it be divided into ten equal parts to correspond to the ten portions of food mentioned above. Upon these equal lines are constructed rectangles, and the area of each rectangle may be assumed to represent the utility of the increment of food corresponding to its base. Thus the utility of the last increment is small, being proportional to the small rectangle on x. As we approach towards
o, each increment bears a larger rectangle, that standing upon
III being the largest complete rectangle. The utility of the next increment, II, is undefined, as also that of I, since these portions of food would be indispensable to life, and their utility, therefore, infinitely great.
We can now form a clear notion of the utility of the whole food, or of any part of it, for we have only to add together the proper rectangles. The utility of the first half of the food will be the sum of the rectangles standing on the line
oa; that of the second half will be represented by the sum of the smaller rectangles between
a and
b. The total utility of the food will be the whole sum of the rectangles, and will be infinitely great.
The comparative utility of the several portions is, however, the most important point. Utility may be treated
*54 as
a quantity of two dimensions, one dimension consisting in the quantity of the commodity, and another in the intensity of the effect produced upon the consumer. Now, the quantity of the commodity is measured on the horizontal line
ox, and the intensity of utility will be measured by the length of the upright lines, or
ordinates. The intensity of utility of the third increment is measured either by
pq, or
p’q’, and its utility is the product of the units in
pp’ multiplied by those in
pq.
But the division of the food into ten equal parts is an arbitrary supposition. If we had taken twenty or a hundred or more equal parts, the same general
principle would hold true, namely, that each small portion would be less useful and necessary than the last. The law may be considered to hold true theoretically, however small the increments are made; and in this way we shall at last reach a figure which is undistinguishable from a continuous curve. The notion of infinitely small quantities of food may seem absurd as regards the consumption of one individual; but, when we consider the consumption of a nation as a whole, the consumption may well be conceived to increase or diminish by quantities which are, practically speaking, infinitely small compared with the whole consumption. The laws which we are about to trace out are to be conceived as theoretically true of the individual; they can only be practically verified as regards the aggregate transactions, productions, and consumptions of a large body of people. But the laws of the aggregate depend of course upon the laws applying to individual cases.
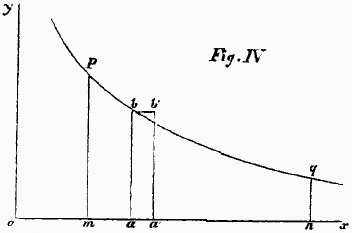 The law of the variation of the degree of utility of food may thus be represented by a continuous curve
The law of the variation of the degree of utility of food may thus be represented by a continuous curve
pbq (Fig. IV.), and the perpendicular height of each point of the curve above the line
ox, represents the degree of utility of the commodity when a certain amount has been consumed.
Thus, when the quantity
oa has been consumed, the degree of utility corresponds to the length of the line
ab; for if we take a very little more food,
aá, its utility will be the product of
aá and
ab very nearly, and more nearly the less is the magnitude of
aá. The degree of utility is thus properly measured by the height of a very narrow rectangle corresponding to a very small quantity of food, which theoretically ought to be infinitely small.
Total Utility and Degree of Utility.
We are now in a position to appreciate perfectly the difference between the
total utility of any commodity and
the degree of utility of the commodity at any point. These are, in fact, quantities of altogether different kinds, the first being represented by an area, and the second by a line. We must consider how we may express these notions in appropriate mathematical language.
Let
x signify, as is usual in mathematical books, the quantity which varies independently,—in this case the quantity of commodity. Let
u denote the
whole utility proceeding from the consumption of
x. Then
u will be, as mathematicians say,
a function of x; that is, it will vary in some continuous and regular,
but probably unknown, manner, when
x is made to vary. Our great object at present, however, is to express the
degree of utility.
Mathematicians employ the sign
D prefixed to a sign of quantity, such as
x, to signify that a quantity of the same nature as
x, but small in proportion to
x, is taken into consideration. Thus
Dx means a small portion of
x, and
x +
Dx is therefore a quantity a little greater than
x. Now, when
x is a quantity of commodity, the utility of
x +
Dx will be more than that of
x as a general rule. Let the whole utility of
x +
Dx be denoted by
u +
Du; then it is obvious that the increment of utility
Du belongs to the increment of commodity
Dx; and if, for the sake of argument, we suppose the degree of utility uniform over the whole of
Dx, which is nearly true owing to its smallness, we shall find the corresponding degree of utility by dividing
Du by
Dx.
We find these considerations fully illustrated by Fig. IV., in which
oa represents
x, and
ab is the degree of utility at the point
a. Now, if we increase
x by the small quantity
aá, or
Dx, the utility is increased by the small rectangle
abb’a’, or
Du; and, since a rectangle is the product of its sides, we find that the length of the line
ab, the degree of utility, is represented by the fraction
Du/
Dx.
As already explained, however, the utility of a commodity may be considered to vary with perfect continuity, so that we commit a small error in assuming
it to be uniform over the whole increment
Dx. To avoid this we must imagine
Dx to be reduced to an infinitely small size,
Du decreasing with it. The smaller the quantities are the more nearly we shall have a correct expression for
ab, the degree of utility at the point
a. Thus the
limit of this fraction
Du/
Dx or, as it is commonly expressed,
du/
dx, is the degree of utility corresponding to the quantity of commodity
x.The degree of utility is, in mathematical language,
the differential coefficient of u considered as a function of x, and will itself be another function of
x.
We shall seldom need to consider the degree of utility except as regards the last increment which has been consumed, or, which comes to the same thing, the next increment which is about to be consumed. I shall therefore commonly use the expression
final degree of utility, as meaning the degree of utility of the last addition, or the next possible addition of a very small, or infinitely small, quantity to the existing stock. In ordinary circumstances, too, the final degree of utility will not be great compared with what it might be. Only in famine or other extreme circumstances do we approach the higher degrees of utility. Accordingly, we can often treat the lower portions of the curves of variation (
pbq, Fig. IV.) which concern ordinary commercial transactions, while we leave out of sight the portions beyond
p or
q. It is also evident that we may know the degree of utility at any
point while ignorant of the total utility, that is, the area of the whole curve. To be able to estimate the total enjoyment of a person would be an interesting thing, but it would not be really so important as to be able to estimate the additions and subtractions to his enjoyment, which circumstances occasion. In the same way a very wealthy person may be quite unable to form any accurate statement of his aggregate wealth; but he may nevertheless have exact accounts of income and expenditure, that is, of additions and subtractions.
Variation of the Final Degree of Utility.
The final degree of utility is that function upon which the Theory of Economics will be found to turn. Economists, generally speaking, have failed to discriminate between this function and the total utility, and from this confusion has arisen much perplexity. Many commodities which are most useful to us are esteemed and desired but little. We cannot live without water, and yet in ordinary circumstances we set no value on it. Why is this? Simply because we usually have so much of it that its final degree of utility is reduced nearly to zero. We enjoy, every day, the almost infinite utility of water, but then we do not need to consume more than we have. Let the supply run short by drought, and we begin to feel the higher degrees of utility, of which we think but little at other times.
The variation of the function expressing the final degree of utility is the all-important point in economic problems. We may state as a general law, that
the degree of utility varies with the quantity of commodity, and ultimately decreases as that quantity increases. No commodity can be named which we continue to desire with the same force, whatever be the quantity already in use or possession. All our appetites are capable of
satisfaction or
satiety sooner or later, in fact, both these words mean, etymologically, that we have had
enough, so that more is of no use to us. It does not follow, indeed, that the degree of utility will always sink to zero. This may be the case with some things, especially the simple animal requirements, such as food, water, air, etc. But the more refined and intellectual our needs become, the less are they capable of satiety. To the desire for articles of taste, science, or curiosity, when once excited, there is hardly a limit.
This great principle of the ultimate decrease of the final degree of utility of any commodity is implied in the writings of many economists, though seldom distinctly stated. It is the real law which lies at the basis of Senior’s so-called “Law of Variety.” Indeed, Senior incidentally states the law itself. He says: “It is obvious that our desires do not aim so much at quantity as at diversity. Not only are there limits to the pleasure which commodities of any given class can afford, but the pleasure diminishes in a rapidly increasing ratio long before those limits are
reached. Two articles of the same kind will seldom afford twice the pleasure of one, and still less will ten give five times the pleasure of two. In proportion, therefore, as any article is abundant, the number of those who are provided with it, and do not wish, or wish but little, to increase their provision, is likely to be great; and, so far as they are concerned, the additional supply loses all, or nearly all, its utility. And, in proportion to its scarcity, the number of those who are in want of it, and the degree in which they want it, are likely to be increased; and its utility, or, in other words, the pleasure which the possession of a given quantity of it will afford, increases proportionally.”
*55
Banfield’s “Law of the Subordination of Wants” also rests upon the same basis. It cannot be said, with accuracy, that the satisfaction of a lower want
creates a higher want; it merely permits the higher want to manifest itself. We distribute our labour and possessions in such a way as to satisfy the more pressing wants first. If food runs short, the all-absorbing question is, how to obtain more, because, at the moment, more pleasure or pain depends upon food than upon any other commodity. But, when food is moderately abundant, its final degree of utility falls very low, and wants of a more complex and less satiable nature become comparatively prominent.
The writer, however, who appears to me to have
most clearly appreciated the nature and importance of the law of utility, is Richard Jennings, who, in 1855, published a small book called the
Natural Elements of Political Economy.*56 This work treats of the physical groundwork of Economics, showing its dependence on physiological laws. It displays great insight into the real basis of Economics; yet I am not aware that economists have bestowed the slightest attention on Jennings’s views.
*57 I give, therefore, a full extract from his remarks on the nature of utility. It will be seen that the law, as I state it, is no novelty, and that careful deduction from principles in our possession is alone needed to give us a correct Theory of Economics.
“To turn from the relative effect of commodities, in producing sensations, to those which are absolute, or dependent only on the quantity of each commodity, it is but too well known to every condition of men, that the degree of each sensation which is produced, is by no means commensurate with the quantity of the commodity applied to the senses…. These effects require to be closely observed, because they are the foundation of the changes of money price, which valuable objects command in times of varied scarcity and abundance; we shall therefore here direct our attention to them for the purpose of
ascertaining the nature of the law according to which the sensations that attend on consumption vary in degree with changes in the quantity of the commodity consumed.
“We may gaze upon an object until we can no longer discern it, listen until we can no longer hear, smell until the sense of odour is exhausted, taste until the object becomes nauseous, and touch until it becomes painful; we may consume food until we are fully satisfied, and use stimulants until more would cause pain. On the other hand, the same object offered to the special senses for a moderate duration of time, and the same food or stimulants consumed when we are exhausted or weary, may convey much gratification. If the whole quantity of the commodity consumed during the interval of these two states of sensation, the state of satiety and the state of inanition, be conceived to be divided into a number of equal parts, each marked with its proper degrees of sensation, the question to be determined will be, what relation does the difference in the degrees of the sensation bear to the difference in the quantities of the commodity?
“First, with respect to all commodities, our feelings show that the degrees of satisfaction do not proceed
pari passu with the quantities consumed; they do not advance equally with each instalment of the commodity offered to the senses, and then suddenly stop; but diminish gradually, until they ultimately disappear, and further instalments can
produce no further satisfaction. In this progressive scale the increments of sensation resulting from equal increments of the commodity are obviously less and less at each step,—each degree of sensation is less than the preceding degree. Placing ourselves at that middle point of sensation, the
juste milieu, the
aurea mediocritas, the
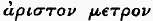 of sages, which is the most usual status of the mass of mankind, and which, therefore, is the best position that can be chosen for measuring deviations from the usual amount, we may say that the law which expresses the relation of degrees of sensation to quantities of commodities is of this character: if the average or temperate quantity of commodities be increased, the satisfaction derived is increased in a less degree, and ultimately ceases to be increased at all; if the average or temperate quantity be diminished, the loss of more and more satisfaction will continually ensue, and the detriment thence arising will ultimately become exceedingly great.”
of sages, which is the most usual status of the mass of mankind, and which, therefore, is the best position that can be chosen for measuring deviations from the usual amount, we may say that the law which expresses the relation of degrees of sensation to quantities of commodities is of this character: if the average or temperate quantity of commodities be increased, the satisfaction derived is increased in a less degree, and ultimately ceases to be increased at all; if the average or temperate quantity be diminished, the loss of more and more satisfaction will continually ensue, and the detriment thence arising will ultimately become exceedingly great.”
*58
Disutility and Discommodity.
A few words will suffice to suggest that as utility corresponds to the production of pleasure, or, at least, a favourable alteration in the balance of pleasure and pain, so negative utility will consist in the production of pain, or the unfavourable alteration of the balance. In reality we must be almost as often
concerned with the one as with the other; nevertheless, economists have not employed any distinct technical terms to express that production of pain, which accompanies so many actions of life. They have fixed their attention on the more agreeable aspect of the matter. It will be allowable, however, to appropriate the good English word
discommodity, to signify any substance or action which is the opposite of
commodity, that is to say,
anything which we desire to get rid of, like ashes or sewage. Discommodity is, indeed, properly an abstract form signifying inconvenience, or disadvantage; but, as the noun
commodities has been used in the English language for four hundred years at least as a concrete term,
*59 so we may now convert discommodity into a concrete term, and speak of
discommodities as substances or things which possess the quality of causing inconvenience or harm. For the abstract notion, the opposite or negative of utility, we may invent the term
disutility, which will mean something different from inutility, or the absence of utility. It is obvious that utility passes through inutility before changing into disutility, these notions being related as +, 0 and -.
Distribution of Commodity in different Uses.
The principles of utility may be illustrated by
considering the mode in which we distribute a commodity when it is capable of several uses. There are articles which may be employed for many distinct purposes: thus, barley may be used either to make beer, spirits, bread, or to feed cattle; sugar may be used to eat, or for producing alcohol; timber may be used in construction, or as fuel; iron and other metals may be applied to many different purposes. Imagine, then, a community in the possession of a certain stock of barley; what principles will regulate their mode of consuming it? Or, as we have not yet reached the subject of exchange, imagine an isolated family, or even an individual, possessing an adequate stock, and using some in one way and some in another. The theory of utility gives, theoretically speaking, a complete solution of the question.
Let
s be the whole stock of some commodity, and let it be capable of two distinct uses. Then we may represent the two quantities appropriated to these uses by
x1 and
y1, it being a condition that
x1 +
y1 =
s. The person may be conceived as successively expending small quantities of the commodity; now it is the inevitable tendency of human nature to choose that course which appears to offer the greatest advantage at the moment. Hence, when the person remains satisfied with the distribution he has made, it follows that no alteration would yield him more pleasure; which amounts to saying that an increment of commodity would yield exactly as much utility in one use as in another. Let
Du1,
Du2, be the increments of
utility, which might arise respectively from consuming an increment of commodity in the two different ways. When the distribution is completed, we ought to have
Du1 =
Du2; or at the limit we have the equation
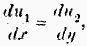
which is true when
x, y are respectively equal to
x1,
y1. We must, in other words, have the
final degrees of utility in the two uses equal.
The same reasoning which applies to uses of the same commodity will evidently apply to any two uses, and hence to all uses simultaneously, so that we obtain a series of equations less numerous by a unit than the number of ways of using the commodity. The general result is that commodity, if consumed by a perfectly wise being, must be consumed with a maximum production of utility.
We should often find these equations to fail. Even when
x is equal to 99/100 of the stock, its degree of utility might still exceed the utility attaching to the remaining 1/100 part in either of the other uses. This would mean that it was preferable to give the whole commodity to the first use. Such a case might perhaps be said to be not the exception but the rule; for, whenever a commodity is capable of only one use, the circumstance is theoretically represented by saying, that the final degree of utility in this employment always exceeds that in any other employment.
Under peculiar circumstances great changes may take place in the consumption of a commodity. In a time of scarcity the utility of barley as food might rise so high as to exceed altogether its utility, even as regards the smallest quantity, in producing alcoholic liquors; its consumption in the latter way would then cease. In a besieged town the employment of articles becomes revolutionised. Things of great utility in other respects are ruthlessly applied to strange purposes. In Paris a vast stock of horses were eaten, not so much because they were useless in other ways, as because they were needed more strongly as food. A certain stock of horses had, indeed, to be retained as a necessary aid to locomotion, so that the equation of the degrees of utility never wholly failed.
Theory of Dimensions of Economic Quantities.
In the recent progress of physical science, it has been found requisite to use notation for the purpose of displaying clearly the natures and relations of the various kinds of quantities concerned. Each different sort of quantity is, of course, expressed in terms of its own appropriate unit—length in terms of yards, or metres; surface, or area, in terms of square yards or square metres; time in terms of seconds, days, or years; and so forth. But the more complicated quantities are evidently related to the simpler ones. Surface is measured by the
square yard—that is to say, the unit of length is involved twice over, and if
by
L we denote one dimension of length, then the dimensions of surface are
LL, or
L2. The dimensions of cubic capacity are in like manner
LLL, or
L3.
In these cases the dimensions all enter
positively, because the number of units in the cubical body, for instance, is found by
multiplying the numbers of units in its length, breadth, and depth. In other cases a dimension enters
negatively. Thus denoting time by
T, it is easy to see that the dimensions of velocity will be
L divided by T, or
LT
-1, because the number of units in the velocity of a body is found by
dividing the units of length passed over by the units of time occupied in passing. In expressing the dimensions of thermal and electric quantities, fractional exponents often become necessary, and the subject assumes the form of a theory of considerable complexity. The reader to whom this branch of science is new will find a section briefly describing it in my
Principles of Science, 3d ed., p. 325, or he may refer to the works there mentioned.
*60
Now, if such a theory of dimensions is requisite in dealing with the precise ideas of physical magnitudes, it seems to be still more desirable as regards the quantities with which we are concerned in Economics. One of the first and most difficult steps in a science is to conceive clearly the nature of the magnitudes
about which we are arguing. Heat was long the subject of discussion and experiment before physicists formed any definite idea how its quantity could be measured and connected with other physical quantities. Yet, until that was done, it could not be considered the subject of an exact science. For one or two centuries economists have been wrangling about wealth, demand and supply, value, production, capital, interest, and the like; but hardly any one could say exactly what were the natures of the quantities in question. Believing that it is in forming these primary ideas that we require to exercise the greatest care, I have thought it well worth the trouble and space to enter fully into a discussion of the dimensions of economic quantities.
Beginning with the easiest and simplest ideas, the
dimensions of commodity regarded merely as a physical quantity will be
the dimensions of mass. It is true that commodities are measured in various ways,—thread by length, carpet by length, corn and liquids by cubic measure, eggs by number, metals and most other goods by weight. But it is obvious that, though the carpet be sold by length, the breadth and the weight of the cloth are equally taken into account in fixing the terms of sale. There will generally be a tacit reference to weight, and through weight to mass of materials in all measurement of commodity. Even if this be not always the case, we may, for the sake of simplifying our symbols in the first treatment of the subject, assume that it is so. We need hardly recede
to any ultimate analysis of the physical conditions of the commodity, but may take it to be measured by
mass, symbolised by
M, the sign usually employed in physical science to denote this dimension.
A little consideration will show, however, that we have really little to do with absolute quantities of commodity. One hundred sacks of corn regarded merely by themselves can have no important meaning for the economist. Whether the quantity is large or small, enough or too much, depends in the first place upon the number of consumers for whom it is intended, and, in the second place, upon the time for which it is to last them. We may perhaps throw out of view the number of consumers in this theory, by supposing that we are always dealing with the single average individual, the unit of which population is made up. Still, we cannot similarly get rid of the element of time. Quantity of supply must necessarily be estimated by the number of units of commodity divided by the number of units in the time over which it is to be expended. Thus it will involve
M positively and
T negatively, and its dimensions will be represented by
MT
-1. Thus in reality
supply should be taken to mean not supply absolutely, but rate of supply.
Consumption of commodity must have the same dimensions. For goods must be consumed in time; any action or effect endures a greater or less time, and commodity which will be abundant for a less time may be scanty for a greater time. To say that
a town consumes fifty million gallons of water is unmeaning
per se. Before we can form any judgment about the statement, we must know whether it is consumed in a day, or a week, or a month.
Following out this course of thought we shall arrive at the conclusion that time enters into all economic questions. We live in time, and think and act in time; we are in fact altogether the creatures of time. Accordingly it is rate of supply, rate of production, rate of consumption, per unit of time that we shall be really treating; but it does not follow that
T
-1 enters into all the dimensions with which we deal.
As was fully explained in Chapter II., the ultimate quantities which we treat in Economics are Pleasures and Pains, and our most difficult task will be to express their dimensions correctly. In the first place, pleasure and pain must be regarded as measured upon the same scale, and as having, therefore, the same dimensions, being quantities of the same kind, which can be added and subtracted; they differ only in sign or direction. Now, the only dimension belonging properly to feeling seems to be
intensity, and this intensity must be independent both of time and of the quantity of commodity enjoyed.
The intensity of feeling must mean, then, the instantaneous state produced by an elementary or infinitesimal quantity of commodity consumed.
Intensity of feeling, however, is only another name for degree of utility, which represents the
favourable effect produced upon the human frame by the consumption of commodity, that is by an elementary or infinitesimal quantity of commodity. Putting
U to indicate this dimension, we must remember that
U will not represent even the full dimensions of the instantaneous state of pleasure or pain, much less the continued state which extends over a certain duration of time. The instantaneous state depends upon the sufficiency or insufficiency of supply of commodity. To enjoy a highly pleasurable condition, a person must want a good deal of commodity, and must be well supplied with it. Now, this supply is, as already explained, rate of supply, so that we must multiply
U by
MT
-1 in order to arrive at the real instantaneous state of feeling. The kind of quantity thus symbolised by
MUT
-1 must be interpreted as meaning
so much commodity producing a certain amount of pleasurable effect per unit of time. But this quantity will not be
quantity of utility itself. It will only be that quantity which, when multiplied by time, will produce quantity of utility. Pleasure, as was stated at the outset, has the dimensions of intensity and duration. It is then this
intensity which is symbolised by
MUT
-1, and we must multiply this last symbol by
T in order to obtain the dimensions of utility or quantity of pleasure produced. But in making this multiplication,
MUT
-1T reduces to
MU, which must therefore be taken to denote the dimensions of
quantity of utility.
We here meet with an explanation of the fact, so
long perplexing to me, that the element of time does not appear throughout the diagrams and problems of this theory relating to utility and exchange. All goes on in time, and time is a necessary element of the question; yet it does not explicitly appear. Recurring to our diagrams, that for instance on p. 46, it is obvious that the dimension
U, or degree of utility, is measured upon the perpendicular axis
oy. The horizontal axis must, therefore, be that upon which rate of supply of commodity or
MT
-1 is measured, strictly speaking. If now we introduce the duration of the utility, we should apparently need a third axis, perpendicular to the plane of the page, upon which to denote it. But were we to introduce this third dimension, we should obtain a solid figure, representing a quantity truly of three dimensions. This would be erroneous, because the third dimension
T enters negatively into the quantity represented by the horizontal axis. Thus time eliminates itself, and we arrive at a quantity of two dimensions correctly represented by a curvilinear area, one dimension of which corresponds to each of the factors in
MU.
This result is at first sight paradoxical; but the difficulty is exactly analogous to that which occurs in the question of interest, and which led so profound a mathematician as Dean Peacock into a blunder, as will be shown in the Chapter upon Capital. Interest of money is proportional to the length of time for which the principal is lent, and also to the amount of money lent and the rate of interest. But this rate of
interest involves time negatively, so that time is ultimately eliminated, and interest emerges with the same dimensions as the principal sum. In the case of utility we begin with a certain absolute stock of commodity,
M. In expending it we must spread it over more or less time, so that it is really rate of supply which is to be considered; but it is this rate
MT
-1, not simply
M, which influences the final degree of utility,
U, at which it is consumed. If the same commodity be made to last a longer time, the degree of utility will be higher, because the necessity of the consumer will be less satisfied. Thus the absolute amount of utility produced will, as a general rule, be greater as the time of expenditure is greater: but this will also be the case with the quantity symbolised by
MU, because the quantity
U will under those circumstances be greater, while
M remains constant.
To clear up the matter still further if possible, I will recapitulate the results we have arrived at.
M means absolute amount of commodity.
MT
-1 means amount of commodity applied, so much per unit of time.
U means the resulting pleasurable effect of any increment of that supply, an infinitesimal quantity supplied per unit of time.
MUT
-1 means therefore so much pleasurable effect produced per unit of commodity per unit of time.
MUT
-1T, or
MU, means therefore so much absolute
pleasurable effect produced by commodity in an unspecified duration of time.
Actual, Prospective, and Potential Utility.
The difficulties of Economics are mainly the difficulties of conceiving clearly and fully the conditions of utility. Even at the risk of being tiresome, I will therefore point out more minutely how various are the senses in which a thing may be said to have utility.
It is quite usual, and perhaps correct, to call iron or water or timber a useful substance; but we may mean by these words at least three distinct facts. We may mean that a particular piece of iron is at the present moment actually useful to some person; or that, although not actually useful, it is expected to be useful at a future time; or we may only mean that it would be useful if it were in the possession of some person needing it. The iron rails of a railway, the iron which composes the Britannia Bridge, or an ocean steamer, is actually useful; the iron lying in a merchant’s store is not useful at present, though it is expected soon to be so; but there is a vast quantity of iron existing in the bowels of the earth, which has all the physical properties of iron, and might be useful if extracted, though it never will be. These are instances of
actual, prospective, and potential utility.
It will be apparent that
potential utility does not
really enter into the science of Economics, and when I speak of
utility simply, I do not mean to include potential utility. It is a question of physical science whether a substance possesses qualities which might make it suitable to our needs if it were within our reach. Only when there arises some degree of probability, however slight, that a particular object will be needed, does it acquire
prospective utility, capable of rendering it a desirable possession. As Condillac correctly remarks:
*61 “On diroit que les choses ne commencent à exister pour eux, qu’au moment o� ils ont un intérêt à savoir qu’elles existent.” But a very large part in industry, and the science of industry, belongs to
prospective utility. We can at any one moment use only a very small fraction of what we possess. By far the greater part of what we hold might be allowed to perish at any moment, without harm, if we could have it re-created with equal ease at a future moment, when need of it arises.
We might also distinguish, as is customary with French economists, between
direct and
indirect utility. Direct utility attaches to a thing like food, which we can actually apply to satisfy our wants. But things which have no direct utility may be the means of procuring us such by exchange, and they may therefore be said to have indirect utility.
*62 To the latter form of utility I have elsewhere applied the name
acquired
utility.*63 This distinction is not the same as that which is made in the Theory of Capital between
mediate and
immediate utility, the former being that of any implement, machine, or other means of procuring commodities possessing
immediate and
direct utility—that is, the power of satisfying want.
*64
Distribution of a Commodity in Time.
We have seen that, when a commodity is capable of being used for different purposes, definite principles regulate its application to those purposes. A similar question arises when a stock of commodity is in hand, and must be expended over a certain interval of time more or less definite. The science of Economics must point out the mode of consuming it to the greatest advantage—that is, with a maximum result of utility. If we reckon all future pleasures and pains as if they were present, the solution will be the same as in the case of different uses. If a commodity has to be distributed over
n days’ use, and
v1,
v2, etc., be the final degrees of utility on each day’s consumption, then we ought clearly to have
v2 =
v3 =…=
vn.
It may, however, be uncertain during how many days we may require the stock to last. The commodity might be of a perishable nature, so that if we were to keep some of it for ten days, it might become unserviceable, and its utility be sacrificed. Assuming
that we can estimate more or less exactly the probability of its remaining good, let
p1,
p2,
p3…
p10, be these probabilities. Then, on the principle (p. 36) that a future pleasure or pain must be reduced in proportion to its want of certainty, we have the equations
r2p2 =… =
v10p10.
The general result is, that as the probability is less, the commodity assigned to each day is less, so that
v, its final degree of utility, will be greater.
So far we have taken no account of the varying influence of an event according to its propinquity or remoteness. The distribution of commodity described is that which should be made and would be made by a being of perfect good sense and foresight. To secure a maximum of benefit in life, all future events, all future pleasures or pains, should act upon us with the same force as if they were present, allowance being made for their uncertainty. The factor expressing the effect of remoteness should, in short, always be unity, so that time should have no influence. But no human mind is constituted in this perfect way: a future feeling is always less influential than a present one. To take this fact into account, let
q1,
q2,
q3, etc., be the undetermined fractions which express the ratios of the present pleasures or pains to those future ones from whose anticipation they arise. Having a stock of commodity in hand, our tendency will be to distribute it so that the following equations will hold true—
v2p2q2 =
v3p3q3 =… =
vnpnqn.
It will be an obvious consequence of these equations that less commodity will be assigned to future days in some proportion to the intervening time.
An illustrative problem, involving questions of prospective utility and probability, is found in the case of a vessel at sea, which is insufficiently victualled for the probable length of the voyage to the nearest port. The actual length of the voyage depends on the winds, and must be uncertain; but we may suppose that it will almost certainly last ten days or more, but not more than thirty days. It is apparent that if the food were divided into thirty equal parts, partial famine and suffering would be certainly endured for the first ten days, to ward off later evils which may not be encountered. To consume one-tenth part of the food on each of the first ten days would be still worse, as almost certainly entailing starvation on the following days. To determine the most beneficial distribution of the food, we should require to know the probability of each day between the tenth and thirtieth days forming part of the voyage, and also the law of variation of the degree of utility of food. The whole stock ought then to be divided into thirty portions, allotted to each of the thirty days, and of such magnitudes that the final degrees of utility multiplied by the probabilities may be equal. Thus, let
v1,
v2,
v3, etc., be the final degrees of utility of the first, second, third, and other days supplied, and
p1,
p2,
p3, etc., the probabilities that the days in
question will form part of the voyage; then we ought to have
p2v2 =
p3v3 =… =
p29v29 =
p30v30.
If these equations did not hold true, it would be beneficial to transfer a small portion from one lot to some other lot. As the voyage is supposed certainly to last the first ten days, we have
p2 =… =
p10 = 1:
hence we must have
v2 =… =
v10:
that is to say, the allotments to the first ten days should be equal. They should afterwards decrease according to some regular law; for, as the probability decreases, the final degree of utility should increase in inverse proportion.
The Character and Logical Method of Political Economy. London, 1857, p. 81. 2d ed. (Macmillan), 1875, pp. 56, 110, 224 App. B.
Voyages.
Illustrations of the Centimetre-gramme-second System of Units, 1875; Fleeming Jenkin’s
Text-Book of Electricity and Magnetism, 1873; Clerk Maxwell’s
Theory of Heat, or the commencement of his great
Treatise on Electricity, vol. i. p. 2.
Le Commerce et le Gouvernement, Seconde Partie, Introduction.
Œuvres Complètes. Paris, 1803. Tom. vii. p. 2.
Traité d’ Economie Politique, 5me ed., p. 11.
Chapter IV
