The Theory of Political Economy
By William Stanley Jevons
THE contents of the following pages can hardly meet with ready acceptance among those who regard the Science of Political Economy as having already acquired a nearly perfect form. I believe it is generally supposed that Adam Smith laid the foundations of this science; that Malthus, Anderson, and Senior added important doctrines; that Ricardo systematised the whole; and, finally, that Mr. J. S. Mill filled in the details and completely expounded this branch of knowledge. Mr. Mill appears to have had a similar notion; for he distinctly asserts that there was nothing; in the Laws of Value which remained for himself or any future writer to clear up. Doubtless it is difficult to help feeling that opinions adopted and confirmed by such eminent men have much weight of probability in their favour. Yet, in the other sciences this weight of authority has not been allowed to restrict the free examination of new opinions and theories; and it has often been ultimately proved that authority was on the wrong side.There are many portions of Economical doctrine which appear to me as scientific in form as they are consonant with facts. I would especially mention the Theories of Population and Rent, the latter a theory of a distinctly mathematical character, which seems to give a clue to the correct mode of treating the whole science. Had Mr. Mill contented himself with asserting the unquestionable truth of the Laws of Supply and Demand, I should have agreed with him. As founded upon facts, those laws cannot be shaken by any theory; but it does not therefore follow, that our conception of Value is perfect and final. Other generally accepted doctrines have always appeared to me purely delusive, especially the so-called Wage Fund Theory. This theory pretends to give a solution of the main problem of the science—to determine the wages of labour; yet, on close examination, its conclusion is found to be a mere truism, namely, that the average rate of wages is found by dividing the whole amount appropriated to the payment of wages by the number of those between whom it is divided. Some other supposed conclusions of the science are of a less harmless character, as, for instance, those regarding the advantage of exchange (see the section on “The Gain by Exchange,” p. 141). [From the Preface to the First Edition]
First Pub. Date
1871
Publisher
London: Macmillan and Co.
Pub. Date
1888
Comments
3rd edition. Includes Preface by Harriet Jevons.
Copyright
The text of this edition is in the public domain. Picture of William Stanley Jevons: Photogravure after a photograph of W. Stanley Jevons, taken by Maull & Co., London., courtesy Liberty Fund, Inc.
Pleasure and Pain as Quantities.
CHAPTER II
THEORY OF PLEASURE AND PAIN
PROCEEDING to consider how pleasure and pain can be estimated as magnitudes, we must undoubtedly accept what Bentham has laid down upon this subject. “To a person,” he says,
*42 “considered
by himself, the value of a pleasure or pain, considered
by itself, will be greater or less according to the four following circumstances:—
(1) Its
intensity.
(2) Its
duration.
(3) Its
certainty or
uncertainty.
(4) Its
propinquity or
remoteness.
These are the circumstances which are to be considered in estimating a pleasure or a pain considered each of them by itself.”
Bentham
*43 goes on to consider three other circumstances which relate to the ultimate and complete result of any act or feeling; these are—
(5)
Fecundity, or the chance a feeling has of being followed by feelings of the same kind: that is, pleasures, if it be a pleasure; pains, if it be a pain.
(6)
Purity, or the chance it has of not being followed by feelings of an opposite kind. And
(7)
Extent, or the number of persons to whom it extends, and who are affected by it.
These three last circumstances are of high importance as regards the theory of morals; but they will not enter into the more simple and restricted problem which we attempt to solve in Economics.
A feeling, whether of pleasure or of pain, must be regarded as having two dimensions, or modes of varying in regard to quantity. Every feeling must last some time, and it may last a longer or shorter time; while it lasts, it may be more or less acute and intense. If in two cases the duration of feeling is the same, that case will produce the greater quantity which is the more intense; or we may say that, with the same duration, the quantity will be proportional to the intensity. On the other hand, if the intensity of a feeling were to remain constant, the quantity of feeling would increase with its duration. Two days of the same degree of happiness are to be twice as much
desired as one day; two days of suffering are to be twice as much feared. If the intensity ever continued fixed, the whole quantity would be found by multiplying the number of units of intensity into the number of units of duration. Pleasure and pain, then, are quantities possessing two dimensions, just as superficies possesses the two dimensions of length and breadth.
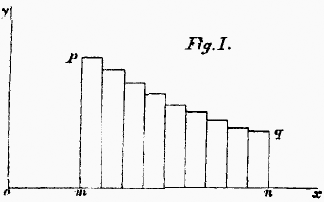 In almost every case, however, the intensity of feeling will change from moment to moment. Incessant variation characterises our states of mind, and this is the source of the main difficulties of the subject. Nevertheless, if these variations can be traced out at all, or any approach to method and law can be detected, it will be possible to form a conception of the resulting quantity of feeling. We may imagine that the intensity changes at the end of every minute, but remains constant in the intervals. The quantity during each minute may be represented, as in Fig. I., by a rectangle whose base is supposed to correspond to the duration of a minute, and whose height is proportional to the intensity of the feeling
In almost every case, however, the intensity of feeling will change from moment to moment. Incessant variation characterises our states of mind, and this is the source of the main difficulties of the subject. Nevertheless, if these variations can be traced out at all, or any approach to method and law can be detected, it will be possible to form a conception of the resulting quantity of feeling. We may imagine that the intensity changes at the end of every minute, but remains constant in the intervals. The quantity during each minute may be represented, as in Fig. I., by a rectangle whose base is supposed to correspond to the duration of a minute, and whose height is proportional to the intensity of the feeling
during the minute in question. Along the line
ox we measure
time, and along parallels to the perpendicular line oy we measure
intensity. Each of the rectangles between
pm and
qn represents the feeling of one minute. The aggregate quantity of feeling generated during the time
mn will then be represented by the aggregate area of the rectangles between
pm and
qn. In this case the intensity of the feeling is supposed to be gradually declining.
But it is an artificial assumption that the intensity would vary by sudden steps and at regular intervals. The error thus introduced will not be great if the intervals of time are very short, and will be less the shorter the intervals are made. To avoid all error, we must imagine the intervals of time to be infinitely short; that is, we must treat the intensity as varying continuously. Thus the proper representation of the variation of feeling is found in a curve of more or less complex character.
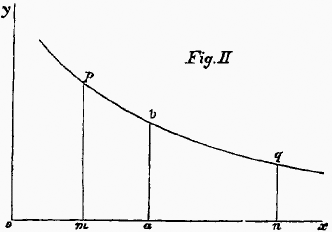 In Fig. II. The height of each point of the curve
In Fig. II. The height of each point of the curve
pq,above the horizontal line
ox, indicates the intensity of feeling in a moment of time; and the whole quantity of feeling generated in the time
mn is measured by the area bounded by the lines
pm,qn,mn, and
pq. The feeling belonging to any other time,
ma, will be measured by the space
mabp cut off by the perpendicular line
ab.
Pain the Negative of Pleasure.
It will be readily conceded that pain is the opposite of pleasure; so that to decrease pain is to increase pleasure; to add pain is to decrease pleasure. Thus we may treat pleasure and pain as positive and negative quantities are treated in algebra. The algebraic sum of a series of pleasures and pains will be obtained by adding the pleasures together and the pains together, and then striking the balance by subtracting the smaller amount from the greater. Our object will always be to maximise the resulting sum in the direction of pleasure, which we may fairly call the positive direction. This object we shall accomplish by accepting everything, and undertaking every action of which the resulting pleasure exceeds the pain which is undergone; we must avoid every object or action which leaves a balance in the other direction.
The most important parts of the theory will turn upon the exact equality, without regard to sign, of the pleasure derived from the possession of an object,
and the pain encountered in its acquisition. I am glad, therefore, to quote the following passage from Mr. Bain’s treatise on
The Emotions and the Will,*44 in which he exactly expresses the opposition of pleasure and pain:—”When pain is followed by pleasure, there is a tendency in the one, more or less, to neutralise the other. When the pleasure exactly assuages the pain, we say that the two are equivalent, or equal in amount, although of opposite nature, like hot and cold, positive and negative; and when two different kinds of pleasure have the power of satiating the same amount of pain, there is fair ground for pronouncing them of equal emotional power. Just as acids are pronounced equivalent when in amount sufficient to neutralise the same portion of alkali, and as heat is estimated by the quantity of snow melted by it, so pleasures are fairly compared as to their total efficacy on the mind, by the amount of pain that they are capable of submerging. In this sense there may be an effective estimate of degree.”
Anticipated Feeling.
Bentham has stated
*45 that one of the main elements in estimating the force of a pleasure or pain is its
propinquity or
remoteness. It is certain that a very large part of what we experience in life depends not on the actual circumstances of the moment so much as on the anticipation of future
events. As Mr. Bain says,
*46 “The foretaste of pleasure is pleasure begun: every actual delight casts before it a corresponding ideal.” Every one must have felt that the enjoyment actually experienced at any moment is but limited in amount, and usually fails to answer to the anticipations which have been formed. “Man never is but always to be blest” is a correct description of our ordinary state of mind; and there is little doubt that, in minds of much intelligence and foresight, the greatest force of feeling and motive arises from the anticipation of a long-continued future.
Now, between the actual amount of feeling anticipated and that which is felt there must be some natural relation, very variable no doubt according to circumstances, the intellectual standing of the race, or the character of the individual; and yet subject to some general laws of variation. The intensity of present anticipated feeling must, to use a mathematical expression, be
some function of the future actual feeling and of the intervening time, and it must increase as we approach the moment of realisation. The change, again, must be less rapid the farther we are from the moment, and more rapid as we come nearer to it. An event which is to happen a year hence affects us on the average about as much one day as another; but an event of importance, which is to take place three days hence, will probably affect us on each of the intervening days more acutely than the last.
This power of anticipation must have a large influence in Economics; for upon it is based all accumulation of stocks of commodity to be consumed at a future time. That class or race of men who have the most foresight will work most for the future. The untutored savage, like the child, is wholly occupied with the pleasures and the troubles of the moment; the morrow is dimly felt; the limit of his horizon is but a few days off. The wants of a future year, or of a lifetime, are wholly unforeseen. But, in a state of civilisation, a vague though powerful feeling of the future is the main incentive to industry and saving. The cares of the moment are but ripples on the tide of achievement and hope. We may safely call that man happy who, however lowly his position and limited his possessions, can always hope for more than he has, and can feel that every moment of exertion tends to realise his aspirations. He, on the contrary, who seizes the enjoyment of the passing moment without regard to coming times, must discover sooner or later that his stock of pleasure is on the wane, and that even hope begins to fail.
Uncertainty of Future Events.
In admitting the force of anticipated feeling, we are compelled to take account of the uncertainty of all future events. We ought never to estimate the value of that which may or may not happen as if it would certainly happen. When it is as likely as not
that I shall receive £100, the chance is worth but £50, because if, for a great many times in succession, I purchase the chance at this rate, I shall almost certainly neither lose nor gain. The test of correct estimation of probabilities is that the calculations agree with fact on the average. If we apply this rule to all future interests, we must reduce our estimate of any feeling in the ratio of the numbers expressing the probability of its occurrence. If the probability is only one in ten that I shall have a certain day of pleasure, I ought to anticipate the pleasure with one-tenth of the force which would belong to it if certain. In selecting a course of action which depends on uncertain events, as, in fact, does everything in life, I should multiply the quantity of feeling attaching to every future event by the fraction denoting its probability. A great casualty, which is very unlikely to happen, may not be so important as a slight casualty which is nearly sure to happen. Almost unconsciously we make calculations of this kind more or less accurately in all the ordinary affairs of life; and in systems of life, fire, marine, or other insurance, we carry out the calculations to great perfection. In all industry directed to future purposes, we must take similar account of our want of knowledge of what is to be.
Essay on the Nature and Conduct of the Passions and Affections, 1728, pp. 34-43, 126, etc.
Chapter III
