The Theory of Political Economy
By William Stanley Jevons
THE contents of the following pages can hardly meet with ready acceptance among those who regard the Science of Political Economy as having already acquired a nearly perfect form. I believe it is generally supposed that Adam Smith laid the foundations of this science; that Malthus, Anderson, and Senior added important doctrines; that Ricardo systematised the whole; and, finally, that Mr. J. S. Mill filled in the details and completely expounded this branch of knowledge. Mr. Mill appears to have had a similar notion; for he distinctly asserts that there was nothing; in the Laws of Value which remained for himself or any future writer to clear up. Doubtless it is difficult to help feeling that opinions adopted and confirmed by such eminent men have much weight of probability in their favour. Yet, in the other sciences this weight of authority has not been allowed to restrict the free examination of new opinions and theories; and it has often been ultimately proved that authority was on the wrong side.There are many portions of Economical doctrine which appear to me as scientific in form as they are consonant with facts. I would especially mention the Theories of Population and Rent, the latter a theory of a distinctly mathematical character, which seems to give a clue to the correct mode of treating the whole science. Had Mr. Mill contented himself with asserting the unquestionable truth of the Laws of Supply and Demand, I should have agreed with him. As founded upon facts, those laws cannot be shaken by any theory; but it does not therefore follow, that our conception of Value is perfect and final. Other generally accepted doctrines have always appeared to me purely delusive, especially the so-called Wage Fund Theory. This theory pretends to give a solution of the main problem of the science—to determine the wages of labour; yet, on close examination, its conclusion is found to be a mere truism, namely, that the average rate of wages is found by dividing the whole amount appropriated to the payment of wages by the number of those between whom it is divided. Some other supposed conclusions of the science are of a less harmless character, as, for instance, those regarding the advantage of exchange (see the section on “The Gain by Exchange,” p. 141). [From the Preface to the First Edition]
First Pub. Date
1871
Publisher
London: Macmillan and Co.
Pub. Date
1888
Comments
3rd edition. Includes Preface by Harriet Jevons.
Copyright
The text of this edition is in the public domain. Picture of William Stanley Jevons: Photogravure after a photograph of W. Stanley Jevons, taken by Maull & Co., London., courtesy Liberty Fund, Inc.
Accepted Opinions concerning Rent.
CHAPTER VI
THEORY OF RENT
THE general correctness of the views put forth in preceding chapters derives great probability from their close resemblance to the Theory of Rent, as it has been accepted by English writers for nearly a century. It has not been usual to state this theory in mathematical symbols, and clumsy arithmetical illustrations have been employed instead; but it is easy to show that the fluxional calculus is the branch of mathematics which most correctly applies to the subject.
The Theory of Rent was first discovered and clearly stated by James Anderson in a tract published in 1777, and called
An Inquiry into the Nature of the Corn Laws, with a view to the Corn Bill proposed for Scotland. An extract from this work may be found in MacCulloch’s edition of the
Wealth of Nations, p. 453, giving a most clear explanation of the effect of the various fertility of land,
and showing that it is not the rent of land which determines the price of its produce, but the price of the produce which determines the rent of the land. The following passage must be given in Anderson’s own words:—
*112
“… In every country there is a variety of soils, differing considerably from one another in point of fertility. These we shall at present suppose arranged into different classes, which we shall denote by the letters A, B, C, D, E, F, etc., the class A comprehending the soils of the greatest fertility, and the other letters expressing different classes of soils, gradually decreasing in fertility as you recede from the first. Now, as the expense of cultivating the least fertile soil is as great or greater than that of the most fertile field, it necessarily follows that if an equal quantity of corn, the produce of each field, can be sold at the same price, the profit on cultivating the most fertile soil must be much greater than that of cultivating the others; and as this continues to decrease as the sterility increases, it must at length happen that the expense of cultivating some of the inferior soils will equal the value of the whole produce.”
The theory really rests upon the principle, which I have called the Law of Indifference, that for the same commodity in the same market there can only be one price or ratio of exchange. Hence, if different qualities of land yield different amounts of produce to the same labour, there must be an excess of profit
in some over others. There will be some land which will not yield the ordinary wages of labour, and which will, therefore, not be taken into cultivation, or if, by mistake, it is cultivated, will be abandoned. Some land will just pay the ordinary wages; better land will yield an excess, so that the possession of such land will become a matter of competition, and the owner will be able to exact as rent from the cultivators the whole excess above what is sufficient to pay the ordinary wages of labour.
There is a secondary origin for rent in the fact, that if more or less labour and capital be applied to the same portion of land, the produce will not increase proportionally to the amount of labour. It is quite impossible that we could go on constantly increasing the yield of one farm without limit, otherwise we might feed the whole country upon a single farm. Yet there is no definite limit; for, by better and better culture, we may always seem able to raise a little more. But the last increment of produce will come to bear a smaller and smaller ratio to the labour required to produce it, so that it soon becomes, in the case of all land, undesirable to apply more labour.
MacCulloch has given, in his edition of the
Wealth of Nations,*113 a supplementary note, in which he explains, with the utmost clearness and scientific accuracy, the nature of the theory. This note contains by far the best statement of the theory, as it
seems to me, and I will therefore quote his recapitulation of the principles which he establishes.
“1. That if the produce of land could always be increased in proportion to the outlay on it, there would be no such thing as rent.
“2. That the produce of land cannot, at an average, be increased in proportion to the outlay, but may be indefinitely increased in a less proportion.
“3. That the least productive portion of the outlay, which, speaking generally, is the last, must yield the ordinary profits of stock. And
“4. That all which the other portions yield more than this, being above ordinary profits, is rent.”
A most satisfactory account of the theory is also given in James Mill’s
Elements of Political Economy, a work which I never read without admiring its brief, clear, and powerful style. James Mill constantly uses the expression
dose of capital. “The time comes,” he says, “at which it is necessary either to have recourse to land of the second quality, or to apply a second dose of capital less productively upon land of the first quality.” He evidently means by a
dose of capital a little more capital, and though the name is peculiar, the meaning is simply that of an
increment of capital. The number of doses or increments mentioned is only three, but this is clearly to avoid prolixity of explanation. There is no reason why we
should not consider the whole capital divided into many more doses. The same general law which makes the second dose less productive than the first, will make a hundredth dose, speaking generally, less productive than the preceding ninety-ninth dose. Theoretically speaking, there is no need or possibility of stopping at any limit. A mathematical law is in theory always continuous, so that the
doses considered are indefinitely small and indefinitely numerous. I consider, then, that James Mill’s mode of expression is exactly equivalent to that which I have adopted in earlier parts of this book. As mathematicians have invented a precise and fully recognised mode of expressing
doses or increments, I know not why we should exclude language from Economics which is found convenient in all other sciences. It is mere pedantry to insist upon calling that a
dose in Economics, which in all the other sciences is called by the perfectly established and expressive term
increment.
The following are James Mill’s general conclusions as to the nature of Rent.
*114 “In applying capital, either to lands of various degrees of fertility, or in successive doses to the same land, some portions of the capital so employed are attended with a greater produce, some with a less. That which yields the least yields all that is necessary for reimbursing and rewarding the capitalist. The capitalist will receive no more than this remuneration for any portion
of the capital which he employs, because the competition of others will prevent him. All that is yielded above this remuneration the landlord will be able to appropriate. Rent, therefore, is the difference between the return yielded to that portion of the capital which is employed upon the land with the least effect, and that which is yielded to all the other portions employed upon it with a greater effect.”
Symbolic Statement of the Theory.
The accepted Theory of Rent, as given above, needs little or no alteration to adapt it to expression in mathematical symbols. For doses or increments of capital I shall substitute increments of labour, partly because the functions of capital remain to be considered in the next chapter, and partly because James Mill, J. S. Mill, and MacCulloch hold the application of capital to be synonymous with the application of labour. This assumption is implied in James Mill’s statement (p. 13); it is expressly stated in J. S. Mill’s
First Fundamental Proposition concerning the Nature of Capital;*115 and MacCulloch adds a footnote
*116 to make it clear, that as all capital was originally produced by labour, the application of additional capital is the application of additional labour. “Either the one phrase or the other may be used indiscriminately.” This doctrine is in itself altogether erroneous, but it will not be erroneous to assume as a mode of
simplifying the problem that the increments of labour applied are equally assisted by capital. It is a separate and subsequent problem to determine how rent or interest arises when the same labour is assisted by different quantities of capital.
I shall suppose that a certain labourer, or, what comes to exactly the same thing, a body of labourers, expend labour on several different pieces of ground. On what principle will they distribute their labour between the several pieces? Let us imagine that a certain amount has been spent upon each, and that another small portion,
Dl, is going to be applied. Let there be two pieces of land, and let
Dx1,
Dx2, be the increments of produce to be expected from the pieces respectively. They will naturally apply the labour to the land which yields the greatest result. So long as there is any advantage in one use of labour over another, the most advantageous will certainly be adopted. Therefore, when they are perfectly satisfied with the distribution made, the increment of produce to the same labour will be equal in each case; or we have
Dx2.
To attain scientific accuracy, we must decrease the increments infinitely, and then we obtain the equation—
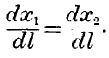
Now
dx/
dl represents the ratio of produce, or the productiveness of labour, as regards the last increment of labour applied. We may say, then, that whenever a
labourer or body of labourers distribute their labour over pieces of land with perfect economy, the
final ratios of produce to labour will be equal.
We may now take into account the general law, that when more and more labour is applied to the same piece of land, the produce ultimately does not increase proportionately to the labour. This means that the function
dx/
dl diminishes without limit towards zero after
x has passed a certain quantity. The whole produce of a piece of land is
x, the whole labour spent upon it is
l; and
x varies in some way as
l varies, never decreasing when
l increases. We may say, then, that
x is a function of
l; let us call it
Pl. When a little more labour is expended, the increment of produce
dx is
dPl, and
dPl/
dl is the final rate of production, the same as was previously denoted by
dx/
dl .
In the Theory of Labour it was shown that no increment of labour would be expended unless there was sufficient recompense in the produce, but that labour would be expended up to the point at which the increment of utility exactly equals the increment of pain incurred in acquiring it. Here we find an exact definition of the amount of labour which will be profitably applied.
It was also shown that the last increment of labour is the most painful, so that if a person is recompensed for the last increment of labour which he applies to
land by the rate of production
dx/
dl, it follows that all the labour he applies might be recompensed sufficiently at the same rate. The whole labour is
l, so that if the recompense were equal over the whole, the result would be
l · (
dx/
dl). Consequently, he obtains more than the necessary return to labour by the amount
l ·
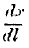;or, as we may write it,
l ·
P‘
l,
in which
P‘
l is the differential coefficient of
Pl, or the final rate of production. This expression represents the advantage he derives from the possession of land in affording him more profit than other methods of employing his labour. It is therefore the rent which he would ask before yielding it up to another person, or equally the rent which he would be able and willing to pay if hiring it from another.
The same considerations apply to every piece of land cultivated. When the same person or body of labourers cultivates several pieces,
P‘
l will be of the same magnitude in each case, but the quantities of labour, and possibly the functions of labour, will be different. Thus with two pieces of land the rent may be represented as
P2l2 – (
l1 +
l2)
P1‘
l1;
or, speaking generally of any number of pieces, it is the sum of the quantities of the form
Pl, minus the sum of the quantities of the form
l.P‘
l.
Illustrations of the Theory.
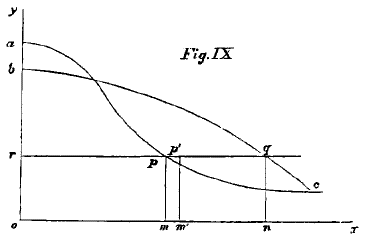It is very easy to illustrate the Theory of Rent by diagrams. For, let distances along the line
ox denote quantities of labour, and let the curve
apc represent the variation of the rate of production, so that the area of the curve will be the measure of the produce. Thus when labour has been applied to the amount
om, the produce will correspond to the area
apmo. Let a small new increment of labour,
mm‘, be applied, and suppose the rate of production equal over the whole of the increment. Then the small parallelogram,
pp‘
m‘
m, will be the produce. This will be proportional in quantity to
pm, so that the height of any point of the curve perpendicularly above a point of the line
ox represents the rate of production at that point in the application of labour.
If we further suppose that the labourer considers his labour,
mm‘, repaid by the produce
pm‘, there is no reason why any other part of his labour should not
be repaid at the same rate. Drawing, then, a horizontal line,
rpq, through the point
p, his whole labour,
om, will be repaid by the produce represented by the area
orpm. Consequently, the overlying area,
rap, is the excess of produce which can be exacted from him as rent, if he be not himself the owner of the land.
Imagining the same person to cultivate another piece of land, we might take the curve,
bqc, to represent its productiveness. The same rate of production will repay the labourer in this case as in the last, so that the intersection of the same horizontal line,
rpq, with the curve, will determine the final point of labour,
n. The area,
rn, will be the measure of the sufficient recompense to the whole labour,
on, spent upon the land; and the excess of produce or rent will be the area,
rbq. In a similar manner, any number of pieces of land might be considered. The figure might have been drawn so that the curves would rise on leaving the initial line
oy, indicating that a very little labour will have a poor rate of production; and that a certain amount of labour is requisite to develop the fertility of the soil. This may often or always be the case, as a considerable quantity of labour is generally requisite in first bringing land into cultivation, or merely keeping it in a fit state for use. The laws of rent depend on the undoubted principle, that the curves always
ultimately decline towards the base line
ox, that is, the final rate of production always
ultimately sinks towards zero.
Chapter VII