The Theory of Political Economy
By William Stanley Jevons
THE contents of the following pages can hardly meet with ready acceptance among those who regard the Science of Political Economy as having already acquired a nearly perfect form. I believe it is generally supposed that Adam Smith laid the foundations of this science; that Malthus, Anderson, and Senior added important doctrines; that Ricardo systematised the whole; and, finally, that Mr. J. S. Mill filled in the details and completely expounded this branch of knowledge. Mr. Mill appears to have had a similar notion; for he distinctly asserts that there was nothing; in the Laws of Value which remained for himself or any future writer to clear up. Doubtless it is difficult to help feeling that opinions adopted and confirmed by such eminent men have much weight of probability in their favour. Yet, in the other sciences this weight of authority has not been allowed to restrict the free examination of new opinions and theories; and it has often been ultimately proved that authority was on the wrong side.There are many portions of Economical doctrine which appear to me as scientific in form as they are consonant with facts. I would especially mention the Theories of Population and Rent, the latter a theory of a distinctly mathematical character, which seems to give a clue to the correct mode of treating the whole science. Had Mr. Mill contented himself with asserting the unquestionable truth of the Laws of Supply and Demand, I should have agreed with him. As founded upon facts, those laws cannot be shaken by any theory; but it does not therefore follow, that our conception of Value is perfect and final. Other generally accepted doctrines have always appeared to me purely delusive, especially the so-called Wage Fund Theory. This theory pretends to give a solution of the main problem of the science—to determine the wages of labour; yet, on close examination, its conclusion is found to be a mere truism, namely, that the average rate of wages is found by dividing the whole amount appropriated to the payment of wages by the number of those between whom it is divided. Some other supposed conclusions of the science are of a less harmless character, as, for instance, those regarding the advantage of exchange (see the section on “The Gain by Exchange,” p. 141). [From the Preface to the First Edition]
First Pub. Date
1871
Publisher
London: Macmillan and Co.
Pub. Date
1888
Comments
3rd edition. Includes Preface by Harriet Jevons.
Copyright
The text of this edition is in the public domain. Picture of William Stanley Jevons: Photogravure after a photograph of W. Stanley Jevons, taken by Maull & Co., London., courtesy Liberty Fund, Inc.
Definition of Labour.
CHAPTER V
THEORY OF LABOUR
ADAM SMITH said, “The real price of everything, what everything really costs to the man who wants to acquire it, is the toil and trouble of acquiring it…. Labour was the first price, the original purchase-money, that was paid for all things.”
*102 If subjected to a very searching analysis, this celebrated passage might not prove to be so entirely true as it would at first sight seem to most readers to be. Yet it is substantially true, and luminously expresses the fact that labour is the beginning of the processes treated by economists, as consumption is the end and purpose. Labour is the painful exertion which we undergo to ward off pains of greater amount, or to procure pleasures which leave a balance in our favour. Courcelle-Seneuil
*103 and Hearn have stated the problem of Economics with
the utmost truth and brevity in saying, that it is
to satisfy our wants with the least possible sum of labour.
In defining
labour for the purposes of the economist we have a choice between two courses. In the first place, we may, if we like, include in it
all exertion of body or mind. A game of cricket would, in this case, be labour; but if it be undertaken solely for the sake of the enjoyment attaching to it, the question arises whether we need take it under our notice. All exertion not directed to a distant and distinct end must be repaid simultaneously. There is no account of good or evil to be balanced at a future time. We are not prevented in any way from including such cases in our Theory of Economics; in fact, our Theory of Labour will, of necessity, apply to them. But we need not occupy our attention by cases which demand no calculus. When we exert ourselves for the sole amusement of the moment, there is but one rule needed, namely, to stop when we feel inclined—when the pleasure no longer equals the pain.
It will probably be better, therefore, to take the second course and concentrate our attention on such exertion as is not completely repaid by the immediate result. This would give us a definition nearly the same as that of Say, who defined labour as
“Action suivée, dirigée vers un but.” Labour, I should say, is
any painful exertion of mind or body undergone partly or wholly with a view to future good.*104 It is
true that labour may be both agreeable at the time and conducive to future good; but it is only agreeable in a limited amount, and most men are compelled by their wants to exert themselves longer and more severely than they would otherwise do. When a labourer is inclined to stop, he clearly feels something that is irksome, and our theory will only involve the point where the exertion has become so painful as to nearly balance all other considerations. Whatever there is that is wholesome or agreeable about labour before it reaches this point may be taken as a net profit of good to the labourer; but it does not enter into the problem. It is only when labour becomes effort that we take account of it, and, as Hearn truly says,
*105 “such effort, as the very term seems to imply, is more or less troublesome.” In fact, we must, as will shortly appear, measure labour by the amount of pain which attaches to it.
Quantitative Notions of Labour.
Let us endeavour to form a clear notion of what we mean by amount of labour. It is plain that duration will be one element of it; for a person labouring
uniformly during two months must be allowed to labour twice as much as during one month. But labour may vary also in intensity. In the same time a man may walk a greater or less distance; may saw a greater or less amount of timber; may pump a greater or less quantity of water; in short, may exert more or less muscular and nervous force. Hence amount of labour will be a quantity of two dimensions, the product of intensity and time when the intensity is uniform, or the sum represented by the area of a curve when the intensity is variable.
But intensity of labour may have more than one meaning; it may mean the quantity of work done, or the painfulness of the effort of doing it. These two things must be carefully distinguished, and both are of great importance for the theory. The one is the reward, the other the penalty, of labour. Or rather, as the produce is only of interest to us so far as it possesses utility, we may say that there are three quantities involved in the theory of labour—the amount of painful exertion, the amount of produce, and the amount of utility gained. The variation of utility, as depending on the quantity of commodity possessed, has already been considered; the variation of the
amount of produce will be treated in the next chapter; we will here give attention to the variation of the painfulness of labour.
Experience shows that as labour is prolonged the effort becomes as a general rule more and more painful. A few hours’ work per day may be considered agreeable rather than otherwise; but so soon as the overflowing energy of the body is drained off, it becomes irksome to remain at work. As exhaustion approaches, continued effort becomes more and more intolerable. Jennings has so clearly stated this law of the variation of labour, that I must quote his words.
*106 “Between these two points, the point of incipient effort and the point of painful suffering, it is quite evident that the degree of toilsome sensations endured does not vary directly as the quantity of work performed, but increases much more rapidly, like the resistance offered by an opposing medium to the velocity of a moving body.
“When this observation comes to be applied to the toilsome sensations endured by the working classes, it will be found convenient to fix on a middle point, the average amount of toilsome sensation attending the average amount of labour, and to measure from this point the degrees of variation. If, for the sake of illustration, this average amount be assumed to be of ten hours’ duration, it would follow that, if at any period the amount were to be supposed to be reduced to five hours, the sensations of labour
would be found, at least by the majority of mankind, to be almost merged in the pleasures of occupation and exercise, whilst the amount of work performed would only be diminished by one-half; if, on the contrary, the amount were to be supposed to be increased to twenty hours, the quantity of work produced would only be doubled, whilst the amount of toilsome suffering would become insupportable. Thus, if the quantity produced, greater or less than the average quantity, were to be divided into any number of parts of equal magnitude, the amount of toilsome sensation attending each succeeding increment would be found greater than that which would attend the increment preceding; and the amount of toilsome sensation attending each succeeding decrement would be found less than that which would attend the decrement preceding.”
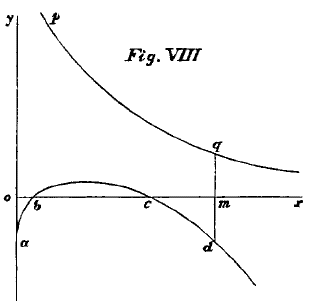There can be no question of the general truth of the above statement, although we may not have the data for assigning the exact law of the variation. We may imagine the painfulness of labour in proportion to produce to be represented by some such curve as
abcd in Fig. VIII. In this diagram the height of points above the line
ox denotes pleasure, and depth below it pain. At the moment of commencing labour it is usually more irksome than when the mind and body are well bent to the work. Thus, at first, the pain is measured by
oa. At
b there is neither pain nor pleasure. Between
b and
c an excess of pleasure is represented as due to the exertion itself.
But after
c the energy begins to be rapidly exhausted, and the resulting pain is shown by the downward tendency of the line
cd.
We may at the same time represent the degree of utility of the produce by some such curve as
pq, the amount of produce being measured along the line
ox. Agreeably to the theory of utility, already given, the curve shows that, the larger the wages earned, the less is the pleasure derived from a further increment. There will, of necessity, be some point
m such that
qm =
dm, that is to say, such that the pleasure gained is exactly equal to the labour endured. Now, if we pass the least beyond this point, a balance of pain will result: there will be an ever-decreasing motive in favour of labour, and an ever-increasing motive against it. The labourer will evidently cease, then, at the point
m. It would be inconsistent with human nature for a man to work when the pain of work
exceeds the desire of possession, including all the motives for exertion.
We must consider the duration of labour as measured by the number of hours’ work per day. The alternation of day and night on the earth has rendered man essentially periodic in his habits and actions. In a natural and wholesome condition a man should return each twenty-four hours to exactly the same state; at any rate, the cycle should be closed within the seven days of the week. Thus the labourer must not be supposed to be either increasing or diminishing his normal strength. But the theory might also be made to apply to cases where special exertion is undergone for many days or weeks in succession, in order to complete work, as in collecting the harvest. Adequate motives may lead to and warrant overwork, but, if long continued, excessive labour reduces the strength and becomes insupportable; and the longer it continues the worse it is, the law being somewhat similar to that of periodic labour.
Symbolic Statement of the Theory.
In attempting to represent these conditions of labour with accuracy, we shall find that there are no less than four quantities concerned; let us denote them as follows:—
t = time, or duration of labour.
l = amount of labour, as meaning the aggregate balance of pain accompanying it, irrespective of the produce.
x = amount of commodity produced.
v = total utility of that commodity.
The amount of commodity produced will be very different in different cases. In any one case the rate of production will be determined by dividing the whole quantity produced by the time of production, provided that the rate of production has been uniform; it will then be
x/
y. But if the rate of production be variable, it can only be determined at any moment by comparing a small quantity of produce with the small portion of time occupied in its production. More strictly speaking, we must ascertain the ratio of an infinitely small quantity of produce to the corresponding infinitely small portion of time. Thus
the rate of production is properly denoted by
Dx/
Dt or at the limit by
dx/
dt.
Again, the degree of painfulness of labour would be
l/
t if it remained invariable; but as it is highly variable, we must again compare small increments, and
Dl/
Dt or, at the limit,
dx/
dt correctly represents the
degree of painfulness of labour. But we must also take into account the fact that the utility of commodity is not constant. If a man works regularly twelve hours a day, he will produce more commodity than in ten hours; therefore the final degree of utility of his commodity, whether he consume it himself or whether he exchange it, will not be quite so high as
when he produced less. This degree of utility is denoted, as before, by
du/
dx the ratio of the increment of utility to the increment of commodity.
The amount of reward of labour can now be expressed; for it is
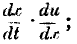
that is to say, it is the product of the ratio of the commodity produced to the time, multiplied by the ratio of the utility to the amount of produce. Thus, the last two hours of work in the day generally gives less reward, both because less produce is then created in proportion to the time spent, and because that produce is less necessary and useful to one who makes enough to support himself in the other ten hours.
We can now ascertain the length of time which should be selected as the most advantageous term of labour. A free labourer endures the irksomeness of work because the pleasure he expects to receive, or the pain he expects to ward off, by means of the produce, exceeds the pain of exertion. When labour itself is a worse evil than that which it saves him from, there can be no motive for further exertion, and he ceases. Therefore he will cease to labour just at the point when the pain becomes equal to the corresponding pleasure gained; and we thus have
t defined by the equation
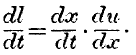
In this, as in the other questions of Economics, all
depends upon the final increments, and we have expressed in the above formula
the final equivalence of labour and utility. A man must be regarded as earning all through his hours of labour an excess of utility; what he produces must be considered not merely the exact equivalent of the labour he gives for it, for it would be, in that case, a matter of indifference whether he laboured or not. As long as he gains, he labours, and when he ceases to gain, he ceases to labour.
In some cases, as in some kinds of machine labour, the rate of production is uniform, or nearly so, and by choice of suitable units may be made equal to unity; the result may then be put more simply in this way. Labour may be considered as expended in successive small quantities,
Dl, each lasting, for instance, for a quarter of an hour; the corresponding benefit derived from the labour will then be denoted by
Du. Now, so long as
Du exceeds in amount of pleasure the negative quantity or pain of
Dl, the difference of sign being disregarded, there will be gain inducing to continued labour. Were
Du to fall below
Dl, there would be more harm than good in labouring; therefore, the boundary between labour and inactivity will be defined by the equality of
Du and
Dl, and at the limit we have the equation
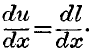
Dimensions of Labour.
If I have correctly laid down, in preceding chapters, the Theory of Dimensions of Utility and Value, there ought not to be much difficulty in stating the similar theory as regards Labour. We might in fact treat labour as simply one case of
disutility or negative utility, that is as pain, or at any rate as a generally painful balance of pleasure and pain, endured in the action of acquiring commodity. Thus its dimensions might be described as identical with those of utility; U would then denote intensity of labour, or degree of labour, just as it was used to denote degree of utility. If we measure labour with respect to the quantity of commodity produced, that is, if we make commodity the variable, then total amount of labour will be the integral of U
dM, and the dimensions of amount of labour will be MU, identical with those of total utility.
If for any reasons of convenience we prefer to substitute a new symbol, specially appropriated to express the dimensions of labour, and say that
intensity of labour is represented by E (Endurance), and
total quantity of labour incurred in the production of certain commodity by ME, it must be remembered that the change is one of convenience only; U and E are essentially quantities of the same nature, and the difference, so far as there is any, arises from the fact that quantities symbolised by E will
usually be negative as compared with those symbolised by U. Labour, however, is often measured and bought and sold by
time, instead of by piecework or commodity produced; in this case, while E continues to express intensity of labour, ET will express the dimensions of amount of labour.
Rate of production will obviously possess the same dimensions as rate of consumption (p. 64), namely, MT
-1, and this quantity forms a link between labour as measured by time and by produce; for ET × MT
-1 = ME. It would be possible to invent various other economic quantities, such as
acceleration of production, with the dimensions MT
-2; but, until it is apparent how such quantities enter into economic theorems, it seems needless to consider them further.
Balance between Need and Labour.
In considering this Theory of Labour an interesting question presents itself. Supposing that circumstances alter the relation of produce to labour, what effect will this have upon the amount of labour which will be exerted? There are two effects to be considered. When labour produces more commodity, there is more reward, and therefore more inducement to labour. If a workman can earn ninepence an hour instead of sixpence, may he not be induced to extend his hours of labour by this increased result? This would doubtless be the case were it not that the very
fact of getting half as much more than he did before, lowers the utility to him of any further addition. By the produce of the same number of hours he can satisfy his desires more completely; and if the irksomeness of labour has reached at all a high point, he may gain more pleasure by relaxing that labour than by consuming more products. The question thus depends upon the direction in which the balance between the utility of further commodity and the painfulness of prolonged labour turns.
In our ignorance of the exact form of the functions either of utility or of labour, it will be impossible to decide this question in an
à priori manner; but there are a few facts which indicate in which direction the balance does usually turn. Statements are given by Porter, in his
Progress of the Nation,*107 which show that when a sudden rise took place in the prices of provisions in the early part of this century, workmen increased their hours of labour, or, as it is said, worked double time, if they could obtain adequate employment. Now, a rise in the price of food is really the same as a decrease of the produce of labour, since less of the necessaries of life can be acquired in exchange for the same money wages. We may conclude, then, that English labourers enjoying little more than the necessaries of life, will work harder the less the produce; or, which comes to the same thing, will work less hard as the produce increases.
Evidence to the like effect is found in the general
tendency to reduce the hours of labour at the present day, owing to the improved real wages now enjoyed by those employed in mills and factories. Artisans, mill-hands, and others, seem generally to prefer greater ease to greater wealth, thus proving that the painfulness of labour varies so rapidly as easily to overbalance the gain of utility. The same rule seems to hold throughout the mercantile employments. The richer a man becomes, the less does he devote himself to business. A successful merchant is generally willing to give a considerable share of his profits to a partner, or to a staff of managers and clerks, rather than bear the constant labour of superintendence himself. There is also a general tendency to reduce the hours of labour in mercantile offices, due to increased comfort and opulence.
It is obvious, however, that there are many intricacies in a matter of this sort. It is not always possible to graduate work to the worker’s liking; in some businesses a man who insisted on working only a few hours a day would soon have no work to do. In the professions of law, medicine, and the like, it is the reputation of enjoying a large practice which attracts new clients. Thus a successful barrister or physician generally labours more severely as his success increases. This result partly depends upon the fact that the work is not easily capable of being performed by deputy. A successful barrister, too, soon begins to look forward to the extrinsic rewards of a high judicial or parliamentary position. But the case of
an eminent solicitor, architect, or engineer is one where the work is to a great extent done by employees, and done without reference to social or political rewards, and where yet the most successful man endures the most labour, or rather is most constantly at work. This indicates that the irksomeness of the labour does not increase so as to over-balance the utility of the increment of reward. In some characters and in some occupations, in short, success of labour only excites to new exertions, the work itself being of an interesting and stimulating nature. But the general rule is to the contrary effect, namely, that a certain success disinclines a man to increased labour. It may be added that in the highest kinds of labour, such as those of the philosopher, scientific discoverer, artist, etc., it is questionable how far great success is compatible with ease; the mental powers must be kept in perfect training by constant exertion, just as a racehorse or an oarsman needs to be constantly exercised.
It is evident that questions of this kind depend greatly upon the character of the race. Persons of an energetic disposition feel labour less painfully than their fellowmen, and, if they happen to be endowed with various and acute sensibilities, their desire of further acquisition never ceases. A man of lower race, a negro for instance, enjoys possession less, and loathes labour more; his exertions, therefore, soon stop. A poor savage would be content to gather the almost gratuitous fruits of nature, if they were sufficient
to give sustenance; it is only physical want which drives him to exertion. The rich man in modern society is supplied apparently with all he can desire, and yet he often labours unceasingly for more. Bishop Berkeley, in his
Querist,*108 has very well asked, “Whether the creating of wants be not the likeliest way to produce industry in a people? And whether, if our (Irish) peasants were accustomed to eat beef and wear shoes, they would not be more industrious?”
Distribution of Labour.
We now come to consider the conditions which regulate the comparative amounts of different commodities produced in a country. Theoretically speaking, we might regard each person as capable of producing various commodities, and dividing his labour according to certain rules between the different employments; it would not be impossible, too, to mention cases where such division does take place. But the result of commerce and the division of labour is usually to make a man find his advantage in performing one trade only; and I give the formulæ as they would apply to an individual, only because they are identical in general character with those which apply to a whole nation.
Suppose that an individual is capeble of producing two kinds of commodity. His sole object, of course, is to produce the greatest amount of utility; but this
will depend partly upon the comparative degrees of utility of the commodities, and partly on his comparative facilities for producing them. Let
x and
y be the respective quantities of the commodities already produced, and suppose that he is about to apply more labour; on which commodity shall he spend the next increment of labour?—Plainly, on that which will yield most utility. Now, if an increment of labour,
Dl, will yield either of the increments of commodity
Dx and
Dy, the ratios of produce to labour, namely,
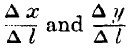
will form one element in the problem. But to obtain the comparative utilities of these commodities, we must multiply respectively by
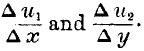
For instance,
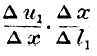
expresses the amount of utility which can be obtained by producing a little more of the first commodity; if this be greater than the same expression for the other commodity, it would evidently be best to make more of the first commodity until it ceased to yield any excess of utility. When the labour is finally distributed, we must have the increments of utility from the several employments equal, and at the limit we have the equation—
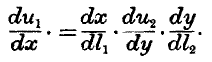
When this equation holds, there can be no motive for altering or regretting the distribution of labour, and the utility produced is at its maximum.
There are in this problem two unknown quantities, namely, the two portions of labour appropriated to the two commodities. To determine them, we require one other equation in addition to the above. If we put
l1 +
l2,
we have still an unknown quantity to determine, namely,
l; but the principles of labour (pp. 172-177) now give us an equation. Labour will be carried on until the increment of utility from any of the employments just balances the increment of pain. This amounts to saying that
du, the increment of utility derived from the first employment of labour, is equal in amount of feeling to
dl1, the increment of labour by which it is obtained. This gives us then the further equation—
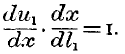
If we pay regard to sign, indeed, we must remember that
dl is, when measured in the same scale as
du, intrinsically negative, but inasmuch as it is given in exchange for
du, which is received, it will in this respect be taken negatively, and thus the above equation holds true.
*109
Relation of the Theories of Labour and Exchange.
It may tend to give the reader confidence in the preceding theories when he finds that they lead directly to the well-known law, as stated in the ordinary language of economists, that value is proportional to the cost of production. As I prefer to state the same law, it is to the effect that the ratio of exchange of commodities will conform in the long run to the
ratio of productiveness, which is the reciprocal of the ratio of the costs of production. The somewhat perplexing relations of these quantities will be fully explained in the next section, but we may now proceed to prove the above result symbolically.
To simplify our expressions, let us substitute for the
rate of productiondx/
dl the symbol
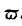. Then
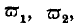express the relative quantities of two different commodities produced by an increment of labour, and we have the following equation, identical with that on page 184.
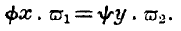
Let us suppose that the person to whom it applies is in a position to exchange with other persons. The conditions of production will now, in all probability, be modified. For
x the quantity of our commodity may perhaps be increased to
x +
x1, and
y diminished to
y –
y1, by an exchange of the quantities
x1 and
y1. If this be so, we shall, as shown in the Theory of Exchange, have the equation
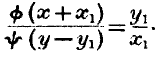
Our equation of production will now be modified, and become
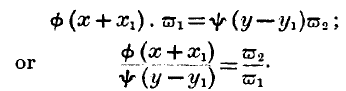
But this equation has its first member identical with the first member of the equation of exchange given above, so that we may at once deduce the all-important equation
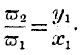
The reader will remember that
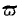expresses the ratio of produce to labour; thus we have proved that commodities will exchange in any market in the ratio of the quantities produced by the same quantity of labour. But as the increment of labour considered is always the final one, our equation also expresses the truth, that
articles will exchange in quantities inversely as the costs of production of the most costly portions, i.e. the last portions added. This result will prove of great importance in the theory of Rent.
Let it be observed that, in uniting the theories of exchange and production, a complicated double adjustment takes place in the quantities of commodity involved. Each party adjusts not only its consumption of articles in accordance with their ratio of exchange, but it also adjusts its production of them. The ratio
of exchange governs the production as much as the production governs the ratio of exchange. For instance, since the Corn Laws have been abolished in England, the effect has been, not to destroy the culture of wheat, but to lessen it. The land less suitable to the growth of wheat has been turned to grazing or other purposes more profitable comparatively speaking. Similarly the importation of hops or eggs or any other article of food does not even reduce the quantity raised here, but prevents the necessity for resorting to more expensive modes of increasing the supply. It is not easy to express in words how the ratios of exchange are finally determined. They depend upon a general balance of producing power and of demand as measured by the final degree of utility. Every additional supply tends to lower the degree of utility; but whether that supply will be forthcoming from any country depends upon its comparative powers of producing different commodities.
Any very small tract of country cannot appreciably affect the comparative supply of commodities: it must therefore adjust its productions in accordance with the general state of the market. The county of Bedford, for instance, would not appreciably affect the markets for corn, cheese, or cattle, whether it devoted every acre to corn or to grazing. Therefore the agriculture of Bedfordshire will have to be adapted to circumstances, and each field will be employed for arable or grazing land according as prevailing prices render one employment or the other more profitable.
But any large country will affect the markets as well as be affected. If the whole habitable surface of Australia, instead of producing wool, could be turned to the cultivation of wine, the wool market would rise, and the wine market fall. If the Southern States of America abandoned cotton in favour of sugar, there would be a revolution in these markets. It would be inevitable for Australia to return to wool and the American States to cotton. These are illustrations of the reciprocal relation of exchange and production.
Relations of Economic Quantities.
I hope that I may sometime be able, in a future and much larger work, to explain in detail the results which can be derived from the mathematical theory expounded in the previous pages. This essay gives them only in an implicit manner. But, before leaving the subject of exchange, it may be well without delay to point out how the results so far set forth connect themselves with the recognised doctrines of political economy. For the sake of accuracy I have avoided the use of the word
value; the expression
cost of production, so continually recurring in most economical treatises, is also here conspicuous by its absence. The reader then, unless he be very careful, may be thrown into some perplexity, when he proceeds to compare my results with those familiar to him elsewhere. I will therefore proceed to trace out the connections between the several quantitative expressions, which
most commonly occur in discussions concerning value, exchange, and production.
In the first place, the ratio of exchange is the actual numerical ratio of the quantities given and received. Let X and Y be the names of the commodities:
x and
y the quantities of them respectively exchanged. Then the ratio of exchange is that of
y to
x. But the value of a commodity in exchange is greater as the quantity received is less, so that the ratio of the quantities dealt with must be the reciprocal of the ratio of the values of the substances, meaning by value the value per unit of the commodity. Thus we may say
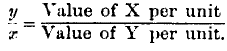
Value is of course very frequently estimated by
price, that is, by the quantity of legal money for which the commodity may be exchanged. Price is indeed ambiguous in the same way as value; it means either the
price of the whole quantity, or the
price per unit of the quantity. Let
p1 be the price per unit of X, and
p2 the similar price of Y. Then it is apparent that
y ×
p2 will be the whole price of
y, and
x ×
p1 will be the whole price of
x. These two must be equal to each other, so that we get
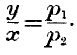
Thus we find that, when price means price per unit, the quantities exchanged are reciprocally as the prices. When price means price of the whole quantity,
the quantities given and received are always of equal price.
Turning now to the production of commodity, it is sufficiently obvious that the cost of production, so far as this expression can be accurately interpreted, varies as the reciprocal of the degree of productiveness. The rate of wages remaining constant, the cost per unit of commodity must of course be lower as the quantity produced in return for a certain amount of wages is greater. Thus we may lay down the equation
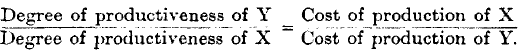
Now, it was shown in pp. 186, 187 that the quantities exchanged are directly proportional to the degrees of productiveness,
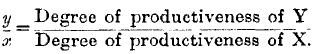
But the ratio of the values is the reciprocal of
y/
x and the ratio of the costs of production is the reciprocal of the other member of the above equation. Thus it follows that
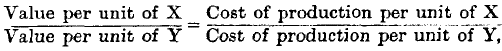
or, in other words,
value is proportional to cost of production. As, moreover, the final degrees of utility of commodities are inversely as the quantities exchanged, it follows that the values per unit are directly proportional to the final degrees of utility.
As it is quite indispensable that the student of political economy should keep the relations of these quantities before his mind with perfect clearness, I repeat the results in several forms of statement. Thus we may group the ratios together—
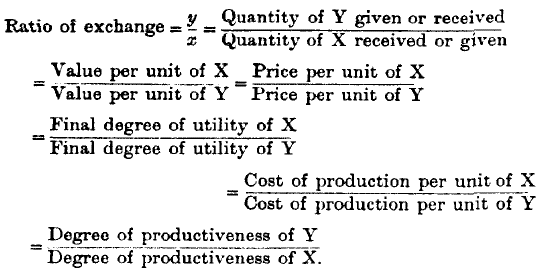
We may state the matter more briefly in the following words:—
The quantities of commodity given or received in exchange are directly proportional to the degrees of productiveness of labour applied to their production, and inversely proportional to the values and prices of those commodities and to their costs of production per unit, as well as to their final degrees of utility. I will even repeat the same statements once more in the form of a diagram—
| Quantities of Commodity exchanged vary | |
|---|---|
| directly as the quantities | inversely as their |
| produced by the same labour. | (1) Values. |
| (2) Prices. | |
| (3) Costs of production. | |
| (4) Final degrees of utility. | |
Various Cases of the Theory.
As we have now reached the principal question in Economics, it will be well to consider the meaning and results of our equations in some detail.
It will, in the first place, be apparent that the absolute facility of producing commodities will not determine the character and amount of trade. The ratio of exchange
y1/
x1 is not determined by
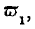nor by
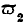separately, but by their comparative magnitudes. If the producing power of a country were doubled, no direct effect would be produced upon the terms of its commerce provided that the increase were equal in all branches of production. This is a point of great importance, which was correctly conceived by Ricardo, and has been fully explained by J. S. Mill.
But though there is no such direct effect, it may happen that there will be an indirect effect through the variation in the degree of utility of different articles. When an increased amount of every commodity can be produced, it is not likely that the increase will be equally desired in each branch of consumption. Hence the degree of utility will fall in some cases more than in others. An alteration of the ratios of exchange must result, and the production of the less needed commodities will not be extended so much as in the case of the more needed ones. We might find in such instances new proofs that value depends not upon labour but upon the degree of utility.
It will also be apparent that nations possessing exactly similar powers of production cannot gain by mutual commerce, and consequently will not have any such commerce, however free from artificial restrictions. We get this result as follows:—Taking
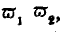as before, to be the final ratios of productiveness in one country, and
m1m2 in a second, then, if the conditions of production are exactly similar, we have
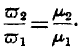
But when a country does not trade at all, its labour and consumption is distributed according to the condition
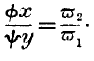
Now, from these equations, it follows necessarily that
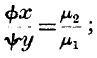
that is to say, the production and consumption already conform to the conditions of production of the second country, and will not undergo any alteration when trade with this country becomes possible.
This is the doctrine usually stated in works on Political Economy, and for which there are good grounds. But I do not think the statement will hold true if the conditions of consumption be very different in two countries. There might be two countries exactly similar in regard to their powers of producing beef and corn, and if their habits of consumption were
also exactly similar, there would be no trade in these articles. But suppose that the first country consumed proportionally more beef, and the second more corn; then, if there were no trade, the powers of the soil would be differently taxed, and different ratios of exchange would prevail. Freedom of trade would cause an interchange of corn for beef. Thus I conclude that it is only where the habits of consumption, as well as the powers of production, are alike, that trade brings no advantage.
The general effect of foreign commerce is to disturb, to the advantage of a country, the mode in which it distributes its labour. Excluding from view the cost of carriage, and the other expenses of commerce, we must always have true
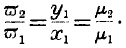
If, then,
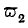was originally less in proportion to
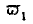than is in accordance with these equations, some labour will be transferred from the production of
y to that of
x until, by the increased magnitude of
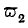and the lessened magnitude of
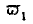equality is brought about.
As in the theory of exchange, so in the theory of production, any of the equations may fail, and the meaning is capable of interpretation. Thus, if the equation
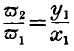
cannot be established, it is impossible that the production
of both commodities,
y and
x, can go on. One of them will be produced at an expenditure of labour constantly out of proportion to that at which it may be had by exchange. If we could not, for instance, import oranges from abroad, part of the labour of the country would probably be diverted from its present employment to raise them; but the cost of production would be always above that of getting them indirectly by exchange, so that free trade necessarily destroys such a wasteful branch of industry It is on this principle that we import the whole of our wines, teas, sugar, coffee, spices, and many other articles from abroad.
The ratio of exchange of any two commodities will be determined by a kind of struggle between the conditions of consumption and production; but here again failure of the equations may take place. In the all-important equations
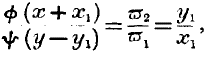
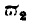expresses the ease with which we may make additions to
y. If we find any means, by machinery or otherwise, of increasing
y without limit, and with the same ease as before, we must, in all probability, alter the ratio of exchange
y1/
x1 in a corresponding degree. But if we could imagine the existence of a large population, within reach of the supposed country, whose desire to consume the quantity
y1 never decreased, however large was the quantity available,
then we should never have
y1/
x1 equal to
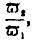
and the producers of
y would make large gains of the nature of rent.
Joint Production.
In one of the most interesting chapters of his
Principles of Political Economy, Book III., chap. xvi., John Stuart Mill has treated of what he calls “Some peculiar Cases of Value.” Under this title he refers to those commodities which are not produced by separate processes, but are the concurrent or joint results of the same operations. “It sometimes happens,” he says, “that two different commodities have what may be termed a joint cost of production. They are both products of the same operation, or set of operations, and the outlay is incurred for the sake of both together, not part for one and part for the other. The same outlay would have to be incurred for either of the two, if the other were not wanted or used at all. There are not a few instances of commodities thus associated in their production. For example, coke and coal-gas are both produced from the same material, and by the same operation. In a more partial sense, mutton and wool are an example; beef, hides, and tallow; calves and dairy produce; chickens and eggs. Cost of production can have nothing to do with deciding the values of the associated commodities relatively to each other. It only decides their joint value…. A principle is wanting
to apportion the expenses of production between the two.” He goes on to explain that, since the cost of production principle fails us, we must revert to a law of value anterior to cost of production, and more fundamental, namely, the law of supply and demand.
On some other occasion I may perhaps more fully point out the fallacy involved in Mill’s idea that he is reverting to
an anterior law of value, the law of supply and demand, the fact being that in introducing the cost of production principle, he had never quitted the laws of supply and demand at all. The cost of production is only one circumstance which governs supply, and thus indirectly influences values.
Again, I shall point out that these cases of joint production, far from being “some peculiar cases,” form the general rule, to which it is difficult to point out any clear or important exceptions. All the great staple commodities at any rate are produced jointly with minor commodities. In the case of corn, for instance, there are the straw, the chaff, the bran, and the different qualities of flour or meal, which are products of the same operations. In the case of cotton, there are the seed, the oil, the cotton waste, the refuse, in addition to the cotton itself. When beer is brewed the grains regularly return a certain price. Trees felled for timber yield not only the timber, but the loppings, the bark, the outside cuts, the chips, etc. No doubt the secondary products are often nearly valueless, as in the case of cinders, slag from blast furnaces, etc. But even these cases go to show all the
more impressively that it is not cost of production which rules values, but the demand and supply of the products.
The great importance of these cases of joint production renders it necessary for us to consider how they can be brought under our theory. Let us suppose that there are two commodities, X and Y, yielded by one same operation, which always produces them in the same ratio, say of
m of X to
n of Y. It might seem at first sight as if this ratio would correspond to the ratio of the degrees of productiveness, as shown a few pages above, that we might say
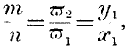
and thus arrive at the conclusion that things jointly produced would always exchange in the ratio of productiveness. But this would be entirely false, because
that equation can only be established when there is freedom of producing one or the other, at each application of a new increment of labour. It is the freedom of varying the quantities of each that allows of the produce being accommodated to the need of it, so that the ratio of the degrees of utility, of the degrees of productiveness, and of the quantities exchanged are brought to equality. But in cases of joint production there is no such freedom; the one substance cannot be made without making a certain fixed proportion of the other, which may have little or no utility.
It will easily be seen, however, that such cases are brought under our theory by simply aggregating
together the utilities of the increments of the joint products. If
dx cannot be produced without
dy, these being the products of the same increment of labour,
dl, then the ratio of produce to labour cannot be written otherwise than as
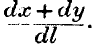
It is impossible to divide up the labour and say that so much is expended on producing X, and so much on Y. But we must estimate separately the utilities of
dx and
dy, by multiplying by their degrees of utility
du1/
dx and
du2/
dx and we then have the aggregate ratio of utility to labour as
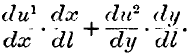
It is plain that we have no equation arising out of these conditions of production, so that the ratio of exchange of X and Y will be governed only by the degrees of utility. But if we compare X and Y with a third commodity Z, as regards its production, we shall arrive at the equation
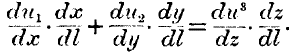
In other words, the increment of utility obtained by applying an increment of labour to the production of Z, must equal the sum of the increments of utility which would be obtained if the same increment of labour were applied to the joint production of X and Y. It is evident that the above equation taken alone
gives us no information as to the ratios existing between the quantities
dx,dy, and
dz. Before we can obtain any ratios of exchange we must have the further equation between the degrees of utility of X and Y, namely,
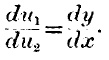
As a general rule, however, any two processes of production will both yield joint products, so that the equation of productiveness will take the form of a sum of increments of utility on both sides, which we may thus write briefly—
du2 +… =
dun +
dun+1 +…
Such an equation becomes then a kind of equation of condition of which the influence may be very slight regarding the ratio of exchange of any two of the commodities concerned. And if in some cases the terms on one side of such an equation are reduced to one or two, it is probably because the other increments of produce are nearly or quite devoid of utility. As in the cases of cinders, chips, sawdust, spent dyes, potato stalks, chaff, etc. etc., almost every process of industry yields refuse results, of which the utility is zero or nearly so. To solve the subject fully, however, we should have to admit negative utilities, as elsewhere explained, so that the increment of utility from any increment
dl of labour would really take the form
du2 ±
du3 ±…
The waste products of a chemical works, for instance,
will sometimes have a low value; at other times it will be difficult to get rid of them without fouling the rivers and injuring the neighbouring estates; in this case they are discommodities and take the negative sign in the equations.
Over-production.
The theory of the distribution of labour enables us to perceive clearly the meaning of
over-production in trade. Early writers on Economics were always in fear of a supposed
glut, arising from the powers of production surpassing the needs of consumers, so that industry would be stopped, employment fail, and all but the rich would be starved by the superfluity of commodities. The doctrine is evidently absurd and self-contradictory. As the acquirement of suitable commodities is the whole purpose of industry and trade, the greater the supplies obtained the more perfectly industry fulfils its purpose. To bring about a universal glut would be to accomplish completely the aim of the economist, which is to maximise the products of labour. But the supplies must be
suitable—that is, they must be in proportion to the needs of the population. Over-production is not possible in all branches of industry at once, but it is possible in some as compared with others. If, by miscalculation, too much labour is spent in producing one commodity, say silk goods, our equations will not hold true. People will be more satiated with silk goods than cotton,
woollen, or other goods. They will refuse, therefore, to purchase them at ratios of exchange corresponding to the labour expended. The producers will thus receive in exchange goods of less utility than they might have acquired by a better distribution of their labour.
In extending industry, therefore, we must be careful to extend it proportionally to all the requirements of the population. The more we can lower the degree of utility of all goods by satiating the desires of the purchasers the better; but we must lower the degrees of utility of different goods in a corresponding manner, otherwise there is an apparent glut and a real loss of labour.
Limits to the Intensity of Labour.
I have mentioned (p. 170) that labour may vary either in duration or intensity, but have yet paid little attention to the latter circumstance. We may approximately measure the intensity of labour by the amount of physical force undergone in a certain time, although it is the pain attending that exertion of force which is the all-important element in Economics. Interesting laws have been or may be detected connecting the amount of work done with the intensity of labour. Even where these laws have not been ascertained, long experience has led men, by a sort of unconscious process of experimentation and inductive reasoning, to select that rate of work which is most advantageous.
Let us take such a simple kind of work as digging. A spade may be made of any size, and if the same number of strokes be made in the hour, the requisite exertion will vary nearly as the cube of the length of the blade. If the spade be small the fatigue will be slight, but the work done will also be slight. A very large spade, on the other hand, will do a great quantity of work at each stroke, but the fatigue will be so great that the labourer cannot long continue at his work. Accordingly, a certain medium-sized spade is adopted, which does not overtax a labourer and prevent him doing a full day’s work, but enables him to accomplish as much as possible. The size of a spade should depend partly upon the tenacity and weight of the material, and partly upon the strength of the labourer. It may be observed that, in excavating stiff clay, navvies use a small strong spade; for ordinary garden purposes a larger spade is employed; for shovelling loose sand or coals a broad capacious shovel is used; and a still larger instrument is employed for removing corn, malt, or any loose light powder.
In most cases of muscular exertion the weight of the body or of some limb is of great importance. If a man be employed to carry a single letter, he really moves a weight of say a hundred and sixty pounds for the purpose of conveying a letter weighing perhaps half an ounce. There will be no appreciable increase of labour if he carries twenty letters, so that his efficiency will be multiplied twenty times. A
hundred letters would probably prove a slight burden, but there would still be a vast gain in the work done. It is obvious, however, that we might go on loading a postman with letters until the fatigue became excessive; the maximum useful result would be obtained with the largest load which does not severely fatigue the man, and trial soon decides the weight with considerable accuracy.
The most favourable load for a porter was investigated by Coulomb, and he found that most work could be done by a man walking upstairs without any load, and raising his burden by means of his own weight in descending. A man could thus raise four times as much in a day as by carrying bags on his back with the most favourable load. This great difference doubtless arises from the muscles being perfectly adapted to raising the human body, whereas any additional weight throws irregular or undue stress upon them. Charles Babbage, also, in his admirable
Economy of Manufactures, has remarked on this subject, and has pointed out that the weight of some limb of the body is an element in all calculations of human labour.
“The fatigue produced on the muscles of the human frame,” says Babbage, “does not altogether depend on the actual force employed in each effort, but partly on the frequency with which it is exerted. The exertion necessary to accomplish every operation consists of two parts: one of these is the expenditure of force which is necessary to drive the tool or instrument;
and the other is the effort required for the motion of some limb of the animal producing the action. In driving a nail into a piece of wood, one of these is lifting the hammer, and
propelling its head against the nail; the other is
raising the arm itself, and moving it in order to use the hammer. If the weight of the hammer is considerable, the former part will cause the greatest portion of the exertion. If the hammer is light, the exertion of
raising the arm will produce the greatest part of the fatigue. It does therefore happen that operations requiring very trifling force, if frequently repeated, will tire more effectually than more laborious work. There is also a degree of rapidity beyond which the action of the muscles cannot be pressed.”
*110
It occurred to me, some time since, that this was a subject admitting of interesting inquiry, and I tried to determine, by several series of experiments, the relation between the amount of work done by certain muscles and the rate of fatigue. One series consisted in holding weights varying from one pound to eighteen pounds in the hand while the arm was stretched out at its full length. The trials were two hundred and thirty-eight in number, and were made at intervals of at least one hour, so that the fatigue of one trial should not derange the next. The average number of seconds during which each weight could be sustained was found to be as follows:—
| Weight in pounds . . | 18 | 14 | 10 | 7 | 4 | 2 | 1 |
| Time in seconds… | 15 | 32 | 60 | 87 | 148 | 219 | 321. |
If the arm had been thus employed in any kind of useful work, we should have estimated the useful effect by the product of the weight sustained and the time. The results would be as follows, in pounds- seconds:—
| Weight… | 18 | 14 | 10 | 7 | 4 | 2 | 1 |
| Useful effect… | 266 | 455 | 603 | 612 | 592 | 438 | 321. |
The maximum of useful effect would here appear to be about seven pounds, which is about the weight usually chosen for dumb-bells and other gymnastic instruments. Details of the other series of experiments are described in an article in
Nature (30th June 1870, vol. ii. p. 158).
I undertook these experiments as a mere illustration of the mode in which some of the laws forming the physical basis of Economics might be ascertained. I was unaware that Professor S. Haughton had already, by experiment, arrived at a theory of muscular action, communicated to the Royal Society in 1862. I was gratified to find that my entirely independent results proved to be in striking agreement with his principles, as was pointed out by Professor Haughton in two articles in
Nature.*111
I am not aware that any exact experiments upon walking or marching have been made, but, as Professor Haughton has remarked to me, they might easily be carried out in the movements of an army. It would only be necessary, on each march which is carried up to the limits of endurance, to register the time and distance passed over. Had we a determination of the exact relations of time, space, and fatigue, it would be possible to solve many interesting problems. For instance, if one person has to overtake another, what should be their comparative rates of walking? Assuming the fatigue to increase as the square of the velocity multiplied by the time, we easily obtain an exact solution, showing that the total fatigue will be least when one person walks twice as quickly as he whom he wishes to overtake.
In different cases of muscular exertion we shall find different problems to solve. The most advantageous rate of marching will greatly depend upon whether the loss of time or the fatigue is the most important. To march at the rate of four miles an hour would soon occasion enormous fatigue, and could only be resorted to under circumstances of great urgency. The distance passed over would bear a much higher ratio to the fatigue at the rate of three, or even two and a half miles an hour. But, if the speed were still further reduced, a loss of strength would again arise, owing to that expended in merely sustaining the body, as distinguished from that of moving it forward.
The Economics of Labour will constantly involve questions of this kind. When a work has to be completed in a brief space of time, workmen may be incited by unusual reward to do far more than their usual amount of work; but so high a rate would not be profitable in other circumstances. The fatigue always rapidly increases when the speed of work passes a certain point, so that the extra result is far more costly in reality. In a regular and constant employment the greatest result will always be gained by such a rate as allows a workman each day, or each week at the most, to recover all fatigue and recommence with an undiminished store of energy.
partly or wholly, and I only give it now as provisionally the best I can suggest. The subject presents itself to me as one of great difficulty, and it is possible that the true solution will consist in treating labour as a case of negative utility, or negative mingled with positive utility. We should thus arrive at a higher generalisation which appears to be foreshadowed in the remarkable work of Hermann Heinrich Gossen described in the preface to this edition. Every act, whether of production or of consumption, may be regarded as producing what Bentham calls a
lot both of pleasures and pains, and the distinction between the two processes will consist in the fact that the algebraic value of the lot in the case of consumption yields a balance of positive utility, while that of production yields a negative or painful balance, at least in that part of the labour involving most effort. In a happy life the negative balance involved in production is more than cleared off by the positive balance of pleasure arising from consumption.
for ‘in this respect be taken negatively,’
read ‘in this respect be taken positively.’ “.—Econlib Editor.]
On the Economy of Machinery and Manufactures, sec. 32, p. 30.
Principles of Animal Mechanics, 1873, pp. 444-450. The subject has since been followed up with much care and ability by Professor Francis E. Nipher, of the Washington University, St. Louis, Missouri, U.S. Details of his experiments will be found in the
American Journal of Science, vol. ix. pp. 130-137; vol. x., etc.;
Nature, vol. xi. pp. 256, 276, etc.
Chapter VI