The Theory of Political Economy

CHAPTER VII
THEORY OF CAPITAL

The Function of Capital.

IN considering the nature and principles of Capital, we enter a distinct branch of our subject. There is no close or necessary connection between the employment of capital and the processes of exchange. Both by the use of capital and by exchange we are enabled vastly to increase the sum of utility which we enjoy; but it is conceivable that we might have the advantages of capital without those of exchange. An isolated man like Alexander Selkirk might feel the benefit of a stock of provisions, tools, and other means of facilitating industry, although cut off from traffic with other men. Economics, then, is not solely the science of Exchange or Value: it is also the science of Capitalisation.

The views which I shall endeavour to establish on this subject are in fundamental agreement with those adopted by Ricardo; but I shall try to put the Theory of Capital in a more simple and consistent manner than has been the case with some later economists. We are told, with perfect truth, that capital consists of wealth employed to facilitate production; but when economists proceed to enumerate the articles of wealth constituting capital, they obscure the subject. "The capital of a country," says Mac-Culloch,*117 "consists of those portions of the produce of industry existing in it which may be directly employed either to support human beings, or to facilitate production." Professor Fawcett again says:*118 "Capital is not confined to the food which feeds the labourers, but includes machinery, buildings, and, in fact, every product due to man's labour which can be applied to assist his industry; but capital which is in the form of food does not perform its functions in the same way as capital that is in the form of machinery: the one is termed circulating capital, the other fixed capital."

The notion of capital assumes a new degree of simplicity as soon as we recognise that what has been called a part is really the whole. Capital, as I regard it, consists merely in the aggregate of those commodities which are required for sustaining labourers of any kind or class engaged in work. A stock of food is the main element of capital; but supplies of clothes, furniture, and all the other articles in common daily use are also necessary parts of capital. The current means of sustenance constitute capital in its free or uninvested form. The single and all-important function of capital is to enable the labourer to await the result of any long-lasting work,—to put an interval between the beginning and the end of an enterprise.

Not only can we, by the aid of capital, erect large works which would otherwise have been impossible, but the production of articles which would have been very costly in labour may be rendered far more easy. Capital enables us to make a great outlay in providing tools, machines, or other preliminary works, which have for their sole object the production of some important commodity, and which will greatly facilitate production when we enter upon it.

Capital is concerned with Time.

Several economists have clearly perceived that the time elapsing between the beginning and end of a work is the difficulty which capital assists us to surmount. Thus James Mill has said: "If the man who subsists on animals cannot make sure of his prey in less than a day, he cannot make sure of his prey in less than a day, he cannot have less than a whole day's subsistence in advance. If hunting excursions are undertaken which occupy a week or a month, subsistence for several days may be required. It is evident, when men come to live upon those productions which their labour raises from the soil, and which can be brought to maturity only once in the year, that subsistence for a whole year must be laid up in advance."*119

Much more recently, Professor Hearn has said, in his admirable work entitled Plutology:*120 "The first and most obvious mode in which capital directly operates as an auxiliary of industry is to render possible the performance of work which requires for its completion some considerable time. In the simplest agricultural operations there is the seed-time and the harvest. A vineyard is unproductive for at least three years before it is thoroughly fit for use. In gold mining there is often a long delay, sometimes even of five or six years, before the gold is reached. Such mines could not be worked by poor men unless the storekeepers gave the miners credit, or, in other words, supplied capital for the adventure. But, in addition to this great result, capital also implies other consequences which are hardly less momentous. One of these is the steadiness and continuity that labour thus acquires. A man, when aided by capital, can afford to remain at his work until it is finished, and is not compelled to leave it incomplete while he searches for the necessary means of subsistence. If there were no accumulated fund upon which the labourer could rely, no man could remain for a single day exclusively engaged in any other occupation than those which relate to the supply of his primary wants. Besides these wants, he should also from time to time search for the materials on which he was to work."

These passages imply, as it seems to me, a clear insight into the nature and purposes of capital, except that the writers have not with sufficient boldness followed out the consequences of their notion. If we take a comprehensive view of the subject, it will be seen that not only the chief but the sole purpose of capital is as above described. Capital simply allows us to expend labour in advance. Thus, to raise corn we need to turn over the surface of the soil. If we proceed straight to the work, and use the implements with which nature has furnished us—our fingers—we should spend an enormous amount of painful labour with very little result. It is far better, therefore, to spend the first part of our labour in making a spade or other implement to assist the rest of our labour. This spade represents so much labour which has been invested, and so far spent; but if it lasts three years, its cost may be considered as repaid gradually during those three years. This labour, like that of digging, has for its object the raising of corn, and the only essential difference is that it has to precede the production of corn by a longer interval. The average interval of time for which labour will remain invested in the spade is half of the three years. Similarly, if we possess a larger capital, and expend it in making a plough, which will last for twenty years, we invest at the beginning a great deal of labour which is only gradually repaid during those twenty years, and which is therefore, on the average, invested for about ten years.

It is true that in modern industry we should seldom or never find the same man making the spade or plough, and afterwards using the implement. The division of labour enables me, with much advantage, to expend a portion of my capital in purchasing the implement from some one who devotes his attention to the manufacture, and probably expends capital previously in facilitating the work. But this does not alter the principles of the matter. What capital I give for the spade merely replaces what the manufacturer had already invested in the expectation that the spade would be needed. Exactly the same considerations may be applied to much more complicated applications of capital. The ultimate object of all industry engaged with cotton is the production of cotton goods. But the complete process of producing those goods is divided into many parts; and it is necessary to begin the spending of labour a long time before any goods can be finished.

In the first place, labour will be required to till the land which is to bear the cotton plants, and probably two years at least will elapse between the time when the ground is first broken and the time when the cotton reaches the mills. A cotton mill, again, must be a very strong and durable structure, and must contain machinery of a very costly character, which can only repay its owner by a long course of use. We might spin and weave cotton goods as in former times, or as it is done in Cashmere, with a very small use of capital; but then the labour required would be enormously greater in proportion to the produce. It is far more economical in the end to spend a vast amount of labour and capital in building a substantial mill and filling it with the best machinery, which will then go on working with unimpaired efficiency for thirty years or more. This means that, in addition to the labour spent in superintending the machines at the moment when goods are produced, a great quantity of labour has been spent from one to thirty years in advance, or, on the average, fifteen years in advance. This expenditure is repaid by an annuity of profit extending over those thirty years.

The interval elapsing between the first exertion of labour and the enjoyment of the result is further increased by any time during which the raw material may lie in warehouses before reaching the machines; and by the time employed in distributing the goods to retail dealers, and through them to the consumers. It may even happen that the consumer finds it desirable to keep a certain stock on hand, so that the time when the real object of the goods is fulfilled becomes still further deferred. During this time, also, capital seems to me to be invested, and only as actual utilisation takes place is expenditure repaid by corresponding utility enjoyed.

I would say, then, in the most general manner, that whatever improvements in the supply of commodities lengthen the average interval between the moment when labour is exerted and its ultimate result or purpose accomplished, such improvements depend upon the use of capital. And I would add that this is the sole use of capital. Whenever we overlook the irrelevant complications introduced by the division of labour and the frequency of exchange, all employments of capital resolve themselves into the fact of time elapsing between the beginning and the end of industry.

Quantitative Notions concerning Capital.

One main point which has to be clearly brought before the mind in this subject is the difference between the amount of capital invested and the amount of investment of capital. The first is a quantity of one dimension only—the quantity of capital; the second is a quantity of two dimensions, namely, the quantity of capital, and the length of time during which it remains invested. If one day's labour remains invested for two years, the capital is only that equivalent to one day; but it is locked up twice as long as if it were invested for only one year. Now all questions in which we consider the most advantageous employment of capital turn upon the length of investment quite as much as upon the amount. The same capital will serve for twice as much industry if it be absorbed or invested for only half the time.

The amount of investment of capital will evidently be determined by multiplying each portion of capital invested at any moment by the length of time for which it remains invested. One pound invested for five years gives the same result as five pounds invested for one year, the product being five pound-years. Most commonly, however, investment proceeds continuously or at intervals, and we must form clear notions on the subject. Thus, if a workman be employed during one year on any work, the result of which is complete, and enjoyed at the end of that time, the absorption of capital will be found by multiplying each day's wages by the days remaining till the end of the year, and adding all the results together. If the daily wages be four shillings, then we have

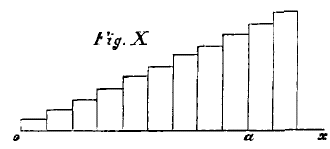We may also represent the investment by a diagram such as Fig. X. The length along the line ox indicates the duration of investment, and the height attained at any point, a, is the amount of capital invested. But it is the whole area of the rectangles up to any point, a, which measures the amount of investment during the time oa.

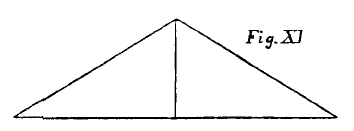The whole result of continued labour is not often consumed and enjoyed in a moment; the result generally lasts for a certain length of time. We must then conceive the capital as being progressively uninvested. Let us, for sake of simple illustration, imagine the labour of producing the harvest to be continuously and equally expended between the first of September in one year and the same day in the next. Let the harvest be then completely gathered, and its consumption begin immediately and continue equally during the succeeding twelve months. Then the amount of investment of capital will be represented by the area of an isosceles triangle, as in Fig. XI., the base of which corresponds to two years of duration. Now the area of a triangle is equal to the height multiplied by half the base; and as the height represents the greatest amount invested, that upon the first of September, when the harvest is gathered; half the base, or one year, is the average time of investment of the whole amount.

In the 37th proposition of the first book of Euclid it is proved that all triangles upon the same base and between the same parallels are equal in area. Hence we may draw the conclusion that, provided capital be invested and uninvested continuously and in simple proportion to the time, we need only regard the greatest amount invested and the greatest time of investment. Whether it be all invested suddenly, and then gradually withdrawn; or gradually invested and suddenly withdrawn; or gradually invested and gradually withdrawn; the amount of investment will be in every case the greatest amount of capital multiplied by half the time elapsing from the beginning to the end of the investment.

Expression for Amount of Investment.

To render our notions of the subject still more exact and general, let us resort once more to mathematical symbols.

Let Dp = amount of capital supposed to be invested in the time Dt; let t = time elapsing before its result is enjoyed, the enjoyment taking place in an interval of time Dt, which may be disregarded in comparison with t. Then t · Dp is the amount of investment; and if the investment is repeated, the sum of the quantities of the nature of t · Dp, or, in the customary mode of expression, St · Dp is the total amount of investment. But it will seldom be possible to assign each portion of result to an exactly corresponding portion of labour. Cotton goods are due to the aggregate industry of those who tilled the ground, grew the cotton, plucked, transported, cleaned, spun, wove, and dyed it; we cannot distinguish the moment when each labourer's work is separately repaid. To avoid this difficulty, we must fix on some moment of time when the whole transaction is closed, all labour upon the ground repaid, the mill and machinery worn out and sold, and the cotton goods consumed. Let t now denote the time elapsing from any moment up to this final moment of closing the accounts. Let Dp be as before an increment of capital invested, and let Dq be an increment of capital uninvested by the sale of the products and their enjoyment by the consumer. Thus it will be pretty obvious that the sum of the quantities t · Dp, less by the sum of the quantities t · Dq will be the total investment of capital, or expressed in symbols St · Dp - St · Dq.

Dimensions of Capital, Credit and Debit.

As the subject presents itself to me at present, I apprehend that capital is to be regarded simply as commodity. If so, the dimension of capital will be represented by M, and the amount of investment of capital, possessing the additional dimension of time, will have the symbol MT. How then are we to determine the quantitative nature of what Senior called Abstinence, that temporary sacrifice of enjoyment which is essential to the existence of capital? Senior thus explicitly defined what he meant by the word:*121 "By the word Abstinence, we wish to express that agent, distinct from labour and the agency of nature, the concurrence of which is necessary to the existence of capital, and which stands in the same relation to profit as labour does to wages." He goes on to explain that abstinence, though usually accompanying labour, is distinct from it. A careful consideration of Senior's remarks shows that in reality abstinence is the endurance of want, the abstaining from the enjoyment of utility which might be enjoyed. Now the degree or intensity of want is measured by the degree of utility of commodity if it were consumed. Great degree of utility simply means great want, so that one dimension of abstinence must be U, and time being also obviously an element of abstinence, the required symbolic statement of its dimensions will be UT. This result satisfactorily corresponds with Senior's definition, for he says that abstinence is to profit as labour is to wages. Now profit or interest is clearly symbolised by M, and wages also by M, both consisting simply of quantities of commodity. Thus UT bears just the same relation to M that ET does to M, for E signifies the degree of painfulness of labour, and can barely be distinguished from U, except in sign.

The relation of abstinence, UT, to total utility, MU, also confirms our result. For if we convert abstinence into satisfaction, by giving a supply of commodity for consumption, this action is symbolically represented by multiplying UT into MT^-1, which yields MU, or utility.

It will need no argument to show that the dimension of debit and credit, having regard only to what is borrowed and owed, will be the dimension of commodity simply, or M. According to the practice of commerce, a contract of debt is a contract to return a certain physically defined quantity of a specified substance, such as an ounce of gold, a ton of pig-iron, a hogshead of palm oil. No attempt is made to define quantities of utility, so that the debt when repaid shall yield utility equal to what it possessed when lent. The borrower and lender either take their chance about this, or provide for it in the rate of interest to be paid. It is equally obvious that in another sense the amount of credit or debit will be proportional to the duration of the operation, and will have the dimensions MT.

Effect of the Duration of Work.

Perhaps the most interesting point in the Theory of Capital is the advantage arising from the rapid performance of work, if it is capable of being done with convenience and with the same ultimate result. To investigate this point, suppose that w = the whole amount of wages which it is requisite to pay in building a house, and that this does not alter when we vary, within certain limits, the time employed in the work, denoted by t. If the work goes on continuously, we shall, during each unit of time, have an amount invested equal to the t^th part of w. The whole amount of investment of capital will therefore be represented by the area of a triangle whose base is t and height w; that is, the investment is ½ tw. Thus when the whole expenditure is ultimately the same, the amount of investment is simply proportional to the time. The result would be more serious if the accumulation of compound interest during the time were taken into account; but the consideration of compound interest would render the formulæ very complex, and is not requisite for the purpose in view.

We must clearly distinguish the case treated above, in which the amount of labour is the same, but spread over a longer time, from other cases where the labour increases in proportion to the time. The investment of capital, then, grows in an exceedingly rapid manner. Neglecting the first cost of tools, materials, and other preparations, let the first day's labour cost a; during the second day this remains invested, and the amount of capital a is added; on each following day a like addition is made. The amount of capital invested is evidently

At beginning	of second	day	a,
At beginning	of third	day	a + a,
At beginning	of fourth	day	a + a + a;

and so on. If the work lasts during n + 1 days, the total amount of investment of capital will be

The sum of the series is

which increases by a term involving the square of the time. The employment of capital thus grows in proportion to the triangular numbers

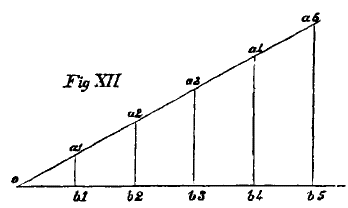If we regard the investment as taking place continuously, the whole absorption of capital is represented by the area of a right-angled triangle (Fig. XII.), in which ob₁, b₁, b₂, b₂ b₃, etc., are the successive units of time. The heights of the lines a₁ b₁, a₂ b₂ represent the amounts invested at the ends of the times. The daily investment being a, the total amount of investment will be a(n²/2), increasing as the square of the time.

Cases of this kind continually occur, as in sinking a deep mine, of which the requisite depth cannot be previously known with accuracy. Any large work, such as a breakwater, an embankment, the foundations of a great bridge, a dock, a long tunnel, the dredging of a channel, involves a problem of a similar nature; for it is seldom known what amount of labour and capital will be required; and if the work lasts much longer than was expected, the result is usually a financial disaster.

Illustrations of the Investment of Capital.

The time during which capital remains invested, and the circumstances of its investment and reproduction, are exceedingly various in different employments. If a person plants cabbages, they will be ready in the course of a few months, and the labour of planting and tending them, together with a part of the labour of preparing and manuring the soil, yields its results with very little delay. In planting a forest tree, however, a certain amount of labour is expended, and no result obtained until after the lapse of thirty, forty, or fifty years. The first cost of enclosing, preparing, and planting a plantation is considerable; and though, after a time, the loppings and thinnings of the trees repay the cost of superintendence and repairs, yet the absorption of capital is great, and we may thus account for the small amount of planting which goes on. The ageing of wine is a somewhat similar case. A certain amount of labour is expended without result for ten or fifteen years, and the cost of storage is incurred during the whole time. To estimate the real cost of the articles at the end of the time, we must, in all such cases, add compound interest, and this grows in a rapid manner. Every pound invested at the commencement of a business becomes 1·63 pounds at the end of ten years, 11·47 pounds at the end of fifty years, and no less than 131·50 pounds at the end of a century, the rate of interest being taken at five per cent. Thus it cannot be profitable to store wine for fifty years, unless it become about twelve times as valuable as it was when new. It cannot pay to plant an oak and let it live a century, unless the timber then repays the cost of planting 132 times.

If an annual charge, however small, has to be incurred (for instance, the cost of storage and superintendence), the expense mounts up in a still more alarming manner. Thus, if the cost of any investment is one pound per annum, the amount invested, with compound interest at five per cent, becomes 12·58 pounds at the end of ten years, 209·35 pounds at the end of fifty years, and the enormous amount of 2610·03 at the end of a century. We shall almost always have to take into account both the original and continuous cost of an investment. Thus if a stock of wine worth £100 be laid by for fifty years, and the cost of storage be £1 per annum, the total cost at the end of the time will be £1147·0 on account of original cost, and £209·35 for storage, or in all £1356·35.

It is to be feared that the rapid accumulation of compound interest is often overlooked in estimating the cost of public works and other undertakings of considerable duration. A great fort, breakwater, or canal (the Caledonian Canal, for instance) is often not completed for twenty years after its commencement, and in the meantime it may be of little or no use. Suppose that its cost has been £10,000 each year; then the aggregate cost would seem to be £200,000, but allowing for interest at five per cent it is really £330,000. The French engineer and economist, Minard,*122 fully understood this point of finance, and showed that in the case of some public works, such as the great digue of Cherbourg harbour, and canals, the execution of which is allowed sometimes to drag on for half a century before any adequate result is returned, the real cost is incomparably greater than it is represented to be by merely stating the sums of money expended. In some cases, such as the first canal of Saint Quentin, a work, after being long prosecuted, is abandoned, and the loss by first cost and interest becomes enormous. The Guernsey Harbour is a case in point, and the English dockyards would supply abundance of similar facts.

An interesting example of the investment of capital occurs in the case of gold and silver, a large stock of which is maintained either in the form of money, or plate and jewellery. Labour is spent in the digging or mining of the metals, which is gradually repaid by the use or satisfaction arising from the possession of the metals during the whole time for which they continue in use. Hence the investment of capital extends over the average duration of the metals. Now, if the stock of gold requires one per cent of its amount to maintain it undiminished, it will be apparent that each particle of gold remains in use 100 years on the average; if ½ per cent is sufficient, the average duration will be 200 years. We may state the result thus:

Loss of gold or silver annually.	Average duration of each particle in use.
1 per cent	100 years
½ per cent	200 years
¼ per cent	400 years
1/10 per cent	1000 years

The wear and loss of the precious metals in a civilised country is probably not more than 1/200 part annually, including plate, jewellery, and money in the estimate, so that the average investment will be for 200 years. It is curious that, if we regard a quantity of gold as wearing away annually by a fixed percentage of what remains, the duration of some part is infinite, and yet the average duration is finite. Some of the gold possessed by the Romans is doubtless mixed with what we now possess; and some small part of it will be handed down as long as the human race exists.

Fixed and Circulating Capital.

Economists have long been accustomed to distinguish capital into the two kinds, fixed and circulating. Adam Smith called that circulating which passes from hand to hand, and yields a revenue by being parted with. The fact of being frequently exchanged is, however, an accidental circumstance which leads to no results of importance. Ricardo altered the use of the terms, applying the name circulating to that which is frequently destroyed and has to be reproduced. He says unequivocally:*123 "In proportion as fixed capital is less durable, it approaches to the nature of circulating capital. It will be consumed, and its value reproduced in a shorter time, in order to preserve the capital of the manufacturer." Accepting this doctrine, and carrying it out to the full extent, we must say that no precise line can be drawn between the two kinds. The difference is one of amount and degree. The duration of capital may vary from a day to several hundred years; the most circulating is the least durable; the most fixed the most durable.

Free and Invested Capital.

I believe that the clear explanation of the doctrine of capital requires the use of a term free capital, which has not been hitherto recognised by economists. By free capital I mean the wages of labour, either in its transitory form of money, or its real form of food and other necessaries of life. The ordinary sustenance requisite to support labourers of all ranks when engaged upon their work is really the true form of capital. It is quite in agreement with the ordinary language of commercial men to say, not that a factory, or dock, or railway, or ship, is capital, but that it represents so much capital sunk in the enterprise. To invest capital is to spend money, or the food and maintenance which money purchases, upon the completion of some work. The capital remains invested or sunk until the work has returned profit, equivalent to the first cost, with interest.

Much clearness would result from making the language of Economics more nearly coincident with that of commerce. Accordingly, I would not say that a railway is fixed capital, but that capital is fixed in the railway. The capital is not the railway, but the food of those who made the railway. Abundance of free capital in a country means that there are copious stocks of food, clothing, and every article which people insist upon having—that, in short, everything is so arranged that abundant subsistence and conveniences of every kind are forth-coming without the labour of the country being much taxed to provide them. In such circumstances it is possible that a part of the labourers of the country can be employed on works of which the utility is distant, and yet no one will feel scarcity in the present.

Uniformity of the Rate of Interest.

A most important principle of this subject is, that free capital can be indifferently employed in any branch or kind of industry. Free capital, as we have just seen, consists of a suitable assortment of all kinds of food, clothing, utensils, furniture, and other articles which a community requires for its ordinary sustenance. Men and families consume much the same kind of commodities, whatever may be the branch of manufacture or trade by which they earn a living. Hence there is nothing in the nature of free capital to determine its employment to one kind of industry rather than another. The very same wages, whether we regard the money wages, or the real wages purchased with the money, will support a man whether he be a mechanic, a weaver, a coal miner, a carpenter, a mason, or any other kind of labourer.

The necessary result is, that the rate of interest for free capital will tend to and closely attain uniformity in all employments. The market for capital is like all other markets: there can be but one price for one article at one time. It is a case of the Law of Indifference (p. 90). Now the article in question is the same, so that its price must be the same. Accordingly, as is well known, the rate of interest, when freed from considerations of risk, trouble, and other interfering causes, is the same in all trades; and every trade will employ capital up to the point at which it just yields the current interest. If any manufacturer or trader employs so much capital in supporting a certain amount of labour that the return is less than in other trades, he will lose; for he might have obtained the current rate by lending it to other traders.

General Expression for the Rate of Interest.

We may obtain a general expression for the rate of interest yielded by capital in any employment provided that we may suppose the produce for the same amount of labour to vary as some continuous function of the time elapsing between the expenditure of the labour and the enjoyment of the result. Let the time in question be t, and the produce for the same amount of labour the function of t denoted by Ft, which may be supposed always to increase with t. If we now extend the time to t + Dt, the produce will be F (t + Dt), and the increment of produce F (t + Dt) - Ft. The ratio which this increment bears to the increment of investment of capital will determine the rate of interest. Now, at the end of the time t, we might receive the product Ft, and this is the amount of capital which remains invested when we extend the time by Dt. Hence the amount of increased investment of capital is Dt · Ft; and, dividing the increment of produce by this last expression, we have

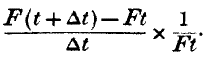
When we reduce the magnitude of Dt infinitely, the limit of the first factor of the above expression is the differential coefficient of Ft, so that we find the rate of interest to be represented by

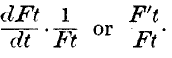
The interest of capital is, in other words, the rate of increase of the produce divided by the whole produce; but this is a quantity which must rapidly approach to zero, unless means can be found of continually maintaining the rate of increase. Unless a body moves with a rapidly increasing speed, the space it moves over in any unit of time must ultimately become inconsiderable compared with the whole space passed over from the commencement. There is no reason to suppose that industry, generally speaking, is capable of returning any such vastly increasing produce from the greater application of capital. Every new machine or other great invention will usually require a fixation of capital for a certain average time, and may be capable of paying interest upon it; but when this average time is reached, it fails to afford a return to more prolonged investments.

To take an instance, let us suppose that the produce of labour in some case is proportional to the interval of abstinence t; then we have say Ft = a · t, in which a is an unknown constant. The differential coefficient F't is now a; and the rate of interest a/Ft or a/at or 1/t; or the rate of interest varies inversely as the time of investment.

Dimension of Interest.

The formula which we obtained in the preceding section has been subjected to close criticism by an eminent mathematician, who proposed several alternative formulæ, but finally accepted my solution of the question as correct. As Professor Adamson, however, has also raised some objections to the formula, it seems desirable to explain its meaning and mode of derivation more fully than was done in the first edition.

In the first place, as regards the theory of dimensions the formula is clearly correct. The rate of interest expresses the ratio which the annual sum paid per annum for the loan of capital bears to the capital. The interest and the capital are quantities of the same nature, their ratio being an abstract number. Dividing by length of time rate of interest will have the dimension T ^-1.

Or we may put it in this way—Interest is paid per annum, or per month, or per other unit of time, and the less the magnitude of this unit, the less must be the numerical expression of the rate of interest. Simple interest at five per cent per annum is 0.416... per cent per month, and so on. Hence time enters negatively, and the dimension of the rate of interest will be T ^-1. Or, again, we may state it thus symbolically—The capital advanced may be taken as having the dimension M; the annual return has the dimensions MT. Dividing the former by the latter we obtain

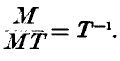
Now the formula F't/Ft clearly agrees with this result; for the denominator is a certain unknown function of the time of advance of the capital t. We may assume that it can be expressed in a finite series of the powers of t, and the numerator, being the differential coefficient of the same function, will be of one degree of power less than Ft. Hence the dimensions of the formula will be

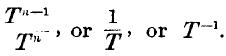
It must be carefully remembered that it is the rate of interest which has the dimension T ^-1, not interest itself, which, being simply commodity of some kind, has the dimension of commodity, namely M, of the same nature, and having the same dimensions.

The function of capital is simply this, that labour which would produce certain commodity m₁, if that commodity were needed immediately for the satisfaction of wants, is applied so as to produce m₂ after the lapse of the time t. The reason for this deferment is that m₂ usually exceeds m₁, and the difference or interest m₂ - m₁ is commodity having the same dimensions as m₁. Hence the rate of interest, apart from the question of time, would be m₂ - m₁ divided by m₁, and the quantities being of the same nature, the ratio will be an abstract number devoid of dimensions. But the time for which the results of labour are foregone is as important a matter as the quantity of commodity. The amount of deferment is m₁t, so that the rate of interest is m₂ - m₁ divided by m₁t, which will have the dimension T ^-1.

Exactly the same result would be obtained, however, if we regarded the use of capital from a different point of view. Capital and deferment of consumption are not needed only in order to increase production, that is to say, the manufacture of goods; they are needed also to equalise consumption, and to allow commodity to be consumed when its utility is at the highest point. Now, when certain commodity is consumed within an interval of time, the utility produced will, as we have seen, possess the dimensions MUT ^-1 T, or MU. Suppose that instead of being consumed within that interval, the commodity is held in hand for a time before being consumed at all. Then the amount of deferment of utility will be proportional both to the interval of time over which it is deferred, and to the utility which is deferred. Thus the amount of deferment will have the dimensions MUT. The increase of utility due to deferment will clearly have the same dimensions as were previously determined, namely MU. Hence the ratio of this increase to the amount of deferment will have the dimensions MU/MUT or T ^-1, and this result corresponds with the dimension of the rate of interest as otherwise reached.

Peacock on the Dimensions of Interest.

The need of some care in forming our conceptions of these quantities is strikingly illustrated by the fact that not quite fifty years ago so profound and philosophic a mathematician as the late Dean Peacock completely misapprehended the matter. In the first edition of his celebrated and invaluable Treatise on Algebra, published in 1830, he gives (§111, p. 91) the interest of money as an example of a quantity of three dimensions, and one which may be represented by a solid. He says: "If p represent the principal or sum of money lent or forborne, r the rate of interest (of £1 for one year), and t the number of years, then the interest accumulated or due will be represented by prt; for if r be the interest of £1 for one year, pr will be the interest of a sum of money denoted by p for one year, and therefore prt will be the amount of this interest in t years, no interest being reckoned upon interest due: such would be the result according to the principles of Arithmetical Algebra.

"If we now suppose prt represented respectively by lines which form the adjacent edges of a parallelopipedon, the solid thus formed will represent the interest accumulated or due: in other words, it will represent whatever is represented by the general formula prt when specific values and significations are given to its symbols: for in whatever manner we may suppose any one of the symbols of prt to vary, the solid will vary in the same proportion.

"The lines which we assume to represent units of p, r, and t, are perfectly arbitrary, whether they are made equal to each other or not: this is clearly the case with p and t, which are quantities of a different nature: and the third quantity is likewise different from the other two, being an abstract numerical quantity: for it expresses the relation between the interest of £1 and £1, or between the interest of £100 and £100, which is the quotient of the division of one quantity by another of the same nature: thus, if the interest be five per cent, then r = 5/100 or 1/20: if four per cent, then r = 4/100 or 1/25: and similarly in other cases: the line, therefore, which is assumed to represent the abstract unit to which r is referred, is independent of the lines which represent units of p and of t, and may therefore be assumed at pleasure, equally with those lines.

"The lines which represent p and t form a rectangular area, which is the geometrical representation of their product: the third quantity r, being merely numerical, may either be represented by a line, as in the case just considered, when a solid parallelopipedon is made the representative of prt: or we may consider the area pt as representing the product prt when r = 1, and that this product in any other case is represented by a rectangle which bears to the rectangle pt the ratio of r to 1: this may be effected by increasing or diminishing one of the sides of the rectangle in the required ratio: the product prt may therefore be correctly represented either by a solid or an area, when one of the factors is an abstract number."

The conclusion at which he arrives is a lame one, for he thinks that the same kind of quantity may be represented indifferently by a solid or an area. The fact is that Peacock confused a product of three factors with a quantity of three dimensions. He took these dimensions as if they were, say M = money, R = rate of interest, and T = time. If we simply multiply these together, as Peacock first does, we get a quantity apparently of three dimensions, MRT. If, according to Peacock's subsequent idea, we take R to be an abstract numerical quantity, then we have two dimensions left, namely, MT. He overlooks the fact that the rate of interest involves time negatively, although he describes r as "the rate of interest (of £1 for one year)." Correctly stated, the dimensions of prt, the quantity of interest are M × T ^-1 × T or M, that is simply the dimension of the money advanced.

If you say, for instance, that the simple interest of £300 at five per cent per annum for five years is £75, there remains no reference in this result to time: £75 is simply £75, and is of exactly the same nature as the £300 which bore the interest.

That Peacock subsequently discovered error, or at least difficulty, in this section, is rendered probable by the fact that he omitted the illustration altogether in his second edition; but he does not, so far as I have observed, give any explanation.

Tendency of Profits to a Minimum.

It is one of the favourite doctrines of economists since the time of Adam Smith, that as society progresses and capital accumulates, the rate of profit, or more strictly speaking, the rate of interest, tends to fall. The rate will always ultimately sink so low, they think, that the inducements to further accumulation will cease. This doctrine is in striking agreement with the result of the somewhat abstract analytical investigation given above. Our formula for the rate of interest shows that unless there be constant progress in the arts, the rate must tend to sink towards zero, supposing accumulation of capital to go on. There are sufficient statistical facts, too, to confirm this conclusion historically. The only question that can arise is as to the actual cause of this tendency.

Adam Smith vaguely attributed it to the competition of capitalists, saying: "The increase of stock which raises wages, tends to lower profit. When the stocks of many rich merchants are turned into the same trade, their mutual competition naturally tends to lower its profit; and when there is a like increase of stock in all the different trades carried on in the same society, the same competition must produce the same effect in them all."*124

Later economists have entertained different views. They attributed the fall of interest to the rise in the cost of labour. The produce of labour, they said, is divided between capitalists and labourers, and if it is necessary to give more to labour, there must be less left to capital, and the rate of profit will fall. I shall discuss the validity of this theory in the final chapter, and will only remark here, that it is not in agreement with the view which I have ventured to take concerning the origin of interest. I consider that interest is determined by the increment of produce which it enables a labourer to obtain, and is altogether independent of the total return which he receives for this labour. Our formula (p. 245) shows that the rate of interest will be greater as the whole produce Ft is less, if the advantage of more capital, measured by F't, remains unchanged. In many ill-governed countries, where the land is wretchedly tilled, the average produce is small, and yet the rate of interest is high, simply because the want of security prevents the due supply of capital: hence more capital is urgently needed, and its price is high. In America and the British Colonies the produce is often high, and yet interest is high, because there is not sufficient capital accumulated to meet all the demands. In England and other old countries the rate of interest is generally lower because there is an abundance of capital, and the urgent need of more is not actually felt.

I conceive that the returns to capital and labour are independent of each other. If the soil yields little, and capital will not make it yield more, then both wages and interest will be low, provided that the capital be not attracted away to more profitable employment. If the soil yields much, and capital will make it yield more, then both wages and interest will be high; if the soil yields much, and capital will not make it yield more, then wages will be high and interest low, unless the capital finds other investments. But the subject is much complicated by the interference of rent. When we speak of the soil yielding much, we must distinguish between the whole yield and the final rate of yield. In the Western States of America the land yields a large total, and all at a high final rate, so that the labourer enjoys the result. In England there is a large total yield, but a small final yield, so that the landowner receives a large rent and the labourer small wages. The more fertile land having here been long in cultivation, the wages of the labourer are measured by what he can earn by cultivating sterile land which it only just pays to take into cultivation.

Advantage of Capital to Industry.

We must take great care not to confuse the rate of interest on capital with the whole advantage which it confers on industry. The rate of interest depends on the advantage of the last increment of capital, and the advantages of previous increments may be greater in almost any ratio. In considering the laws of utility, we found that an article possessing an immensely great total utility, for instance corn or water, might have a very low final degree of utility, because our need of it was almost entirely satisfied; yet the ratio of exchange always depends upon the final, not the previous degree of utility. The case is the same with capital. Some capital may be indispensable to a manufacture; hence the benefit conferred by the capital is indefinitely great, and were there no more capital to be had, the rate of interest which could be demanded, assuming the article manufactured to be necessary, would be almost unlimited. But as soon as ever a larger supply of capital becomes available, the prior benefit of capital is overlooked. As free capital is always the same in quality, the second portion may be made to replace the first if needful: hence capitalists can never exact from labourers the whole advantages which their capital confers—they can exact only a rate determined by the advantage of the last increment. A lender of capital cannot say to a borrower who wants £3000: "I know that £1000 is indispensable to your business, and therefore will charge you 100 per cent interest upon it; for the second £1000, which is less necessary, I will charge twenty per cent; and as upon the third £1000 you can only earn the common profit, I will only ask five percent." The answer would be, that there are many people only earning five per cent on their capital who would be glad to lend enough at a small advance of interest; and it is a matter of indifference who is the lender.

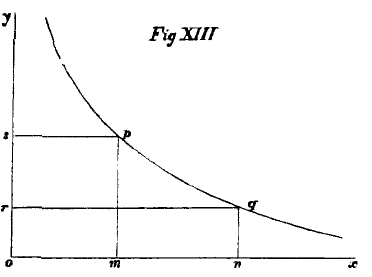The general result of the tendency to uniformity of interest is, that employers of capital always get it at the lowest prevailing rate; they always borrow the capital which is least necessary to others, and either the labourers themselves, or the public generally as consumers, gather all the excess of advantage. To illustrate this result, let distances along the line ox, in Fig. XIII., mark quantities of capital employing in any branch of industry a fixed number of labourers. Let the area of the curve denote the whole produce of labour and capital. Thus to the capital, on, results a produce measured by the area of the curvilinear figure between the upright lines oy and qn. But the amount of increased produce which would be due to an increment of capital would be measured by the line qn, so that this will represent F't (p. 245). The interest of the capital will be its amount, on, multiplied by the rate qn, or the area of the rectangle oq. The remainder of the produce, pqry, will belong to the labourer. But had less capital been available, say not more than om, its rate of interest would have been measured by pm, the amount of interest by the rectangle op, while the labourer must have remained contented with the smaller share, psy. I will not say that the above diagram represents with strict accuracy the relations of capital, produce, wages, rate of interest, and amount of interest; but it may serve roughly to illustrate their relations. I see no way of representing exactly the theory of capital in the form of a diagram.

Are Articles in the Consumers' hands Capital?

The views of the nature of capital expressed in this chapter generally agree with those entertained by Ricardo and various other economists; but there is one point in which the theory leads me to a result at variance with the opinions of almost all writers. I feel quite unable to adopt the opinion that the moment goods pass into the possession of the consumer they cease altogether to have the attributes of capital. This doctrine descends to us from the time of Adam Smith, and has generally received the undoubting assent of his followers. The latter, indeed, have generally omitted all notice of such goods, treating them as if no longer under the view of the economist. Adam Smith, although he denied the possessions of a consumer the name of capital, took care to enumerate them as part of the stock of the community. He divides into three portions the general stock of a country, and while the second and third portions are fixed and circulating capital, the first is described as follows:—*125

"The first is that portion which is reserved for immediate consumption, and of which the characteristic is, that it affords no revenue or profit. It consists in the stock of food, clothes, household furniture, etc., which have been purchased by their proper consumers, but which are not yet entirely consumed. The whole stock of mere dwelling-houses too subsisting at any one time in the country make a part of this first portion. The stock that is laid out in a house, if it is to be the dwelling-house of the proprietor, ceases from that moment to serve in the function of a capital, or to afford any revenue to its owner. A dwelling-house, as such, contributes nothing to the revenue of its inhabitant; and though it is, no doubt, extremely useful to him, it is as his clothes and household furniture are useful to him, which, however, make a part of his expense, and not of his revenue."

MacCulloch, indeed, in his edition of the Wealth of Nations, p. 121, has remarked upon this passage, that "the capital laid out in building houses for such persons is employed as much for the public advantage as if it were vested in the tools or instruments they make use of in their respective businesses." He appears, in fact, to reject the doctrine, and it is surprising that economists have generally acquiesced in Adam Smith's view, though it leads to manifest contradictions. It leads to the absurd conclusion that the very same thing fulfilling the very same purposes will be capital or not according to its accidental ownership. To procure good port wine it is necessary to keep it for a number of years, and Adam Smith would not deny that a stock of wine kept in the wine merchant's possession for this purpose is capital, because it yields him revenue. If a consumer buys it when new, and keeps it to improve, it will not be capital, although it is evident that he gains the same profit as the merchant by buying it at a lower price. If a coal merchant lays in a stock of coal when cheap, to sell when dear, it is capital; but if a consumer lays in a stock, it is not.

Adam Smith's views seem to be founded upon a notion that capital ought to give an annual revenue or increase of wealth like a field yields a crop of corn or grass. Speaking of a dwelling-house, he says: "If it is to be let to a tenant for rent, as the house itself can produce nothing, the tenant must always pay the rent out of some other revenue, which he derives either from labour, or stock, or land. Though a house, therefore, may yield a revenue to its proprietor, and thereby serve in the function of a capital to him, it cannot yield any to the public, nor serve in the function of a capital to it, and the revenue of the whole body of the people can never be in the smallest degree increased by it. Clothes and house-hold furniture, in the same manner, sometimes yield a revenue, and thereby serve in the function of a capital to particular persons. In countries where masquerades are common, it is a trade to let out mas-querade dresses for a night. Upholsterers frequently let furniture by the month or by the year. Undertakers let the furniture of funerals by the day and by the week. Many people let furnished houses, and get a rent, not only for the use of the house, but for that of the furniture. The revenue, however, which is derived from such things, must always be ultimately drawn from some other source of revenue."*126

This notion that people live upon a kind of net revenue flowing in to them appears to be derived from the old French economists, and plays no part in modern Economics. Nothing is more requisite than a dwelling-house, and if a person cannot hire a house at the required spot, he must find capital to build it. I think that no economist would refuse to count among the fixed capital of the country that which is sunk in dwelling-houses. Capital is sunk in farming that we may have bread, in cotton mills that we may be clothed, and why not in houses that we may be lodged? If land yields an annual revenue of corn and wool, milk, beef, and other necessaries, houses yield a revenue of shelter and comfort. The sole end of all industry is to satisfy our wants; and if capital is requisite to supply shelter, and furniture and useful utensils, as it undoubtedly is, why refuse it the name which it bears in all other employments?

Can we deny that the property of a hotel-keeper is capital and yields a revenue to its owner? Yet it is invested in pots and pans, and beds, and all kinds of common furniture. In America it is not uncommon for people to live all their lives in hotels or boarding-houses; and we might readily conceive the system to advance until no one would undertake housekeeping except as a profession. Now if we allow to what is invested in hotels, hired furnished houses, lodgings, and the like, the nature of capital, I do not see how we can refuse it to common houses. We should thus be led into all kinds of absurdities.

For instance, if two people live in their own houses, these are not, according to present opinion, capital; if they find it convenient to exchange houses and pay rent each to the other, the houses are capital. At great watering-places like Brighton it is a regular business to lease houses, fill them with furniture, and then let them for short periods as furnished houses: surely it is capital which is embarked in the trade. If a private individual happens to own a furnished house which he does not at the time want, and lets it, can we refuse to regard his house and furniture as capital? Whenever one person provides the articles and another uses them and pays rent, there is capital. Surely, then, if the same person uses and owns them, the nature of the things is not fundamentally different. There is no need for a money payment to pass; but every person who keeps accurate accounts should debit those accounts with an annual charge for interest and depreciation on what he has invested in house and furniture. Housekeeping is an occupation involving wages, capital and interest, like any other business, except that the owner consumes the whole result.

By accepting this view of the subject, we shall avoid endless difficulties. What, for instance, shall we say to a theatre? Is it not the product of capital? Can it be erected without capital? Does it not return interest, if successful, like any cotton mill or steam vessel? If the economist agrees to this, he must allow, on similar grounds, that a very large part of the aggregate capital of the country is invested in theatres, hotels, schools, lecture rooms, and institutions of various kinds which do not belong to the industry of the country, taken in a narrow sense, but which none the less contribute to the wants of its inhabitants, which is the sole object of all industry.

I may add that even the food, clothes, and many other possessions of extensive classes are often indubitable capital; they are bought upon credit, and interest is undoubtedly paid for the capital sunk in them by the dealers. There is hardly, I suppose, a man of fashion in London who walks in his own clothes, and the tailors find in the practice a very profitable investment for capital. Except among the poorer classes, and often among them, food is seldom paid for until after it is consumed. Interest must be paid one way or another upon the capital thus absorbed. Whether or not these articles in the consumers' hands are capital, at any rate they have capital invested in them—that is, labour has been spent upon them of which the whole benefit is not enjoyed at once.

I might also point out at almost any length, that the stock of food, clothing, and other requisite articles of subsistence in the country are a main part of capital according to the statements of J. S. Mill, Professor Fawcett, and most other economists. Now what does it really matter if these articles happen to lie in the warehouses of traders or in private houses, so long as there is a stock? At present it is the practice for farmers and corn merchants to hold the produce of the harvest until the public buys and consumes it. Surely the stock of corn is capital. But if it were the practice of every housekeeper to buy up corn in the autumn and keep it in a private granary, would it not serve in exactly the same way to subsist the population? Would not everything go on exactly the same, except that every one would be his own capitalist in regard to corn in place of paying farmers and corn merchants for doing the business?