The Demand and Supply of Public Goods
By James M. Buchanan
First Pub. Date
1968
Publisher
Indianapolis, IN: Liberty Fund, Inc.
Pub. Date
1999
Comments
First published in 1968 by Rand McNally & Company. Foreword by Geoffrey Brennan.
Copyright
The text of this edition is copyright ©: 1999 Liberty Fund, Inc. Picture of James M. Buchanan: File photo detail, courtesy Liberty Fund, Inc. James M. Buchanan, Charlottesville, Virginia, 1964.
- Foreword
- Ch. 1, A Methodological Introduction
- Ch. 2, Simple Exchange in a World of Equals
- Ch. 3, Simple Exchange in a World of Unequals
- Ch. 4, Pure and Impure Public Goods
- Ch. 5, Many Private Goods, Many Persons
- Ch. 7, The Publicness of Political Decisions
- Ch. 8, The Institutions of Fiscal Choice
- Ch. 9, Which Goods Should Be Public
- Ch. 10, Toward a Positive Theory of Public Finance
- Supplementary Reading Materials
 Simple Exchange in a World of Unequals
Simple Exchange in a World of Unequals
The several simplifying assumptions that have been imposed on the models of simple exchange have been aimed at laying bare the essentials of the trading process. The characteristics of equilibrium can be generalized since these do not depend on the particular restrictions imposed on the models. Complexities have been obscured in the elementary treatment, however, and it is time to commence the laborious, but fascinating, task of dismantling the simplifications one by one.
The most vulnerable of these involves the complete identity of our two potential traders. Let us start the dismantling process by dropping only the restriction that the two persons in the model have identical preference functions, identical tastes. How will this single change modify our analysis? We adopt methodological partial differentiation here, and keep all of our other assumptions inviolate. We remain in the two-person, two-good world; we assume identity in productive capacity, with simple linear transformation functions. We assume away strategic behavior, and neglect income-effect feedbacks.
 |
| Figure 3.1 |
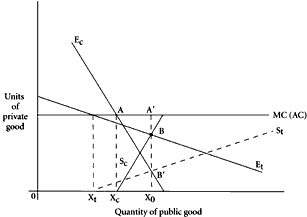
In reference to the tools previously introduced, we shall start here in reverse order, with the Marshallian geometry. The construction developed in
Figure 2.3 can be readily adjusted to allow for differences in tastes between the two persons in the group. Figure 3.1 illustrates this. Two marginal evaluation curves must now be drawn, one for each person. The curve for Tizio is labeled
E
t; that for Caio is labeled
E
c.
In ignorance of the public-goods interdependence, Tizio would aim at producing the quantity 0
X
t anticipating a private consumption of like amount. Caio would, in the same situation, aim at producing the quantity 0
X
c. Let us again assume as we did in the earlier illustration, that Tizio recognizes and acts on the interdependence sooner than Caio. As he does so, he will be motivated to reduce his public-goods production to zero. He will enjoy his “free ride” from the spillover benefits, the external economy, generated by Caio’s production. Caio, waking up somewhat later to the essential interdependence, will find himself at
A, precisely where he expected to find himself in the absence of the interdependence.
The prospects for trade and the position of final trading equilibrium can be shown as in the discussion of Figure 2.3. Beyond the quantity 0
X
c, Tizio will stand ready to subsidize Caio for additional production in the maximum amounts indicated by the curve,
E
t, to the right of
A. Caio in turn will be willing to supply additional units of the public good, for joint consumption, at marginal supply prices indicated by the curve
S
c. This curve is derived by subtracting vertically Caio’s own evaluation curve,
E
c, from the marginal cost curve,
MC. Trading equilibrium is attained at position
B, or at public-goods quantity 0
X0. At the margin, Tizio pays
BX0 in exchange for Caio’s agreement to produce the indicated extension in quantity of the commonly shared good. Caio, in accepting this subsidy which is lower than the marginal cost of production, is himself “paying for” the public good, at the margin, a marginal “price” of
A‘
B.
This construction can be modified without difficulty to allow Tizio to become the marginal producer of the public good. His supply curve, in the marginal sense, becomes
S
t, and the point of intersection between this curve and the evaluation curve for Caio,
E
c, determines trading equilibrium, shown at
B‘. This is precisely the same public-goods output as that shown at
B; only the roles of the two traders have been reversed. At the margin, Tizio is now paying
A‘
B‘, which, by construction, is equal to
BX0. Caio is paying
B‘
X0, which is equal to
A‘
B.
Under the assumption that neglects income-effect feedbacks, the quantity of the public good is not modified by the way in which the two traders grope their way toward final equilibrium. If this income-effect feedback is introduced, the distribution of the net gains to be made from trade over inframarginal units will shift marginal evaluations, and the final position may depend, to a degree, on the precise manner that equilibrium is approached. Again this modification would not change the essential characteristics of the final equilibrium position.
The basic difference between the outcome that emerges in this world-of-unequals and that which was shown to emerge in the world-of-equals is found in the distribution of costs at the margin between the two traders. In the world-of-equals, the model showed the obvious; the cost of the public good must be shared equally at the equilibrium margin of adjustment. This remains true regardless of the possible differentials in the distribution of total costs due to bargaining luck over the inframarginal trading ranges. If we should allow the income-effect feedbacks, this result would not have been forthcoming, since these effects alone would make for differences in the two traders, and would, in one sense, violate the world-of-equals model even with the assumed identity of tastes and productive capacities.
When tastes are allowed to differ, even if we disregard the income effects, this symmetry in marginal-cost shares no longer holds, nor should we expect it to hold. As the construction suggests, shares in the costs of producing the public good at the margin where all trading gains are exhausted will be dependent on the respective marginal evaluations that are placed on the quantity of the good.
Differential Marginal Prices for Public Goods
Only in this unequals model does one of the important differences between equilibrium characteristics in an economy with public goods and those in an economy where all goods are purely private become crystal clear. In the standard neoclassical setting where all goods are privately divisible, all purchasers face the same marginal prices when full equilibrium has been established. What is the basis for this important difference?
With privately divisible goods, a difference in marginal price as between any two persons represents a trading opportunity that remains unexploited. The person confronted with the higher of two prices can gain by purchasing the good through the offices of the person who confronts the lower price. The former will gladly pay something for this unexploited avenue for trade, over and above the external price confronting the latter. And the latter will gladly undertake the indirect purchase for some payment beneath the price that confronts the former. In such situations, price differentials cannot exist except insofar as they reflect genuine “equalizing” differences, in which case they should not be called differentials.
In the case of public goods, no such retrading is possible. By definition, these goods are not privately divisible. Individually, persons cannot adjust their own purchases over varying quantities. The same quantity must be available for each member of the relevant group. But different persons will place different marginal values on any given quantity. If each person is to be in equilibrium in the sense that, for him, the quantity supplied is that which he prefers, differentials in marginal prices must be introduced. And, as the simplified analysis has already indicated, such differentials will come to be established through the processes of trade or exchange.
This interesting difference between equilibrium states in the world of private goods and the world of public goods is worth further examination. What are the dimensions of the quantity units in each case?
Units of Consumption and Units of Production
With privately divisible goods, as these are ordinarily conceived, it is not necessary to answer the question posed above. The unit that is produced or supplied is dimensionally equivalent to the unit that is consumed by some ultimate buyer. A single unit of production implies the availability of a single unit for consumption, by some one person. And this person’s ultimate act in consuming the unit removes all possibility of others’ like consumption of the same unit. It is the absence of this one-to-one relationship that is the basis of the public-goods distinction. With a pure public good, a unit that is produced or supplied is, by definition, simultaneously available for the consumption of all members of the relevant group. Hence, a unit that is supplied is wholly different in dimension from a unit that is consumed. The consumption of a unit by one person does not reduce or remove the possibility of consumption by another person.
This may be put in terms of our simple illustration. A single unit of public-goods supply, mosquito repellent, amounts to two units of consumption, one for Tizio and one for Caio. Care must be taken to keep this dimensional difference in mind; otherwise confusion can easily arise when we discuss some of the complexities in later parts of this book. For example, many economists have referred to the public-goods interdependence as an example of extreme external economies
in consumption. This usage is misleading for the standard illustrations. There need be no external economy stemming from the
act of consuming the good on the part of one individual or the other. The spillover benefit, the external economy, may arise wholly from the act of
producing the good that is
commonly consumed. Note that genuine external economies in consumption can arise, and some of these will be discussed briefly at a later point, but these are not the standard examples for pure public goods. At this early juncture, our interest is restricted to the classic illustrations, e.g., lighthouses, police and fire protection, mosquito control.
Marshall’s Theory of Joint Supply
When it is recognized that the unique element in a public good, as contrasted with a purely private good, is the common sharing of a
jointly supplied unit, we can examine neoclassical economic theory to see what analogies to the modern theory of public goods might have been developed. The theory of joint supply that is found in Marshall’s
Principles is, in its fundamental respects, equivalent to the theory of public goods. This suggests that there may be precious few principles in economics after all.
Marshall conceived his theory in application to physical commodities that could be privately consumed, and there was no joint sharing of final consumption units in his models. For the Marshallian theory the jointness of supply arises because of the technological conditions of producing, not because of the technological conditions of consuming, as in the public goods case. However, as we shall demonstrate, the results that emerge from analysis are identical in the two models.
His classic example involved the joint supply of meat and leather, to which he added wool and mutton, wheat and straw. (The relevant discussion here is found in Alfred Marshall,
Principles of Economics, 8th Edition, pp. 388-390, and Mathematical Note XVIII, p. 854.) The producer or supplier of bullocks simultaneously meets two separate demands, that for meat and that for leather or hides. These final products, desired by different demanders, are jointly supplied in the process of breeding and growing steers, necessarily so, under Marshall’s initial assumption that the relative proportions of the final products in each unit of supply are fixed. Meat and leather are, of course, demonstrably different products at the stage of final demand, different in a superficially descriptive sense. The single unit of supply embodies two separate units of consumption. And no observing economist would predict that the equilibrium price for the meat contained in one bullock (the unit of supply) need be equal to the equilibrium price for the hides contained in the same bullock.
We can review Marshall’s analysis by converting it into our own, Tizio-Caio model of two-person, two-good exchange. Assume, as before, that both persons produce and consume coconuts privately. For our second good, however, let us now substitute bullocks for mosquito repellent. Tizio, we shall say, uses hides for clothing; Caio has no use for hides at all. On the other hand, Caio eats meat; Tizio does not. Under these assumptions, the jointly supplied unit is, in effect, a purely public good because of the technology of production. Strictly speaking, we should also require the additional restriction that withholding of unused product is somehow impossible. Note that the problem in this converted Marshallian supply situation has become in almost all respects identical to that discussed in the earlier mosquito repellent illustration. The fact that, at the final or ultimate stage of consumption, the consumption units appear descriptively different in one model and similar in the other is irrelevant. In equilibrium, Tizio’s demand price for leather or hides plus Caio’s demand price for meat, both defined in terms of the quantities contained in the unit of supply, must just be equal to the marginal supply price of the jointly-produced unit.
This example can be readily discussed in terms of the geometry of Figure 3.1. In that construction, we did not draw in a combined or aggregate demand curve, derived by a vertical summation of the two separate marginal evaluation curves, but, had we done so, this aggregate curve would have cut the marginal cost curve at A’; the position of equilibrium determined in this way would have been identical with that previously discussed. If we think of the public good as being produced by third parties, external to our two persons (or two groups of demanders) this alternative construction which employs the summed marginal evaluation curves becomes somewhat more meaningful. In such a model, Tizio and Caio trade, not with each other alone, but with some external supplier of the public good, and the analysis becomes almost purely Marshallian.
Concentration on the Marshallian theory of joint supply allows several features of the public-goods problem to be clarified. First of all, Marshall’s treatment, in its strict sense, depends for its validity on the assumption that supply is genuinely joint. If the proportions of meat and hides can be modified by the producers of steers, the analysis becomes considerably more difficult. With the public-goods model, however, this requirement of technological jointness in production is not required. If we define a good to be purely public, the analogue to fixity in proportions is guaranteed. The equal availability of the
same quantity of the good, measured in units of supply, to all persons precludes any shifting in proportions. The relevance of this characteristic of public goods, which we may call extreme nonexclusion, may be questioned. As we shall demonstrate in a later chapter, however,
any good or service can be treated as a purely public good, provided that it is organized through an institutional structure embodying the extreme publicness features. Technological characteristics of production or consumption need not be present for the analysis to be germane to the real-world fiscal structure as this structure, in fact, operates.
Marshall used his theory of joint supply to make predictions. He predicted that, under the restrictions of his model, a decrease in the demand for meat would tend to increase the equilibrium price for hides. We can do precisely the same thing with our public-goods model. In the two-person case, let us suppose that Caio becomes partially immune to mosquito bites; his demand for the commonly shared good falls. As a result, in any new equilibrium position, Tizio must contribute a larger cost of producing the good at the margin of adjustment. Or, conversely, suppose that Caio’s demand should increase. Here, equilibrium output of the public good will increase and Tizio will find himself paying a somewhat lower marginal price.
Predictions of this nature have relevance beyond the oversimplified models that we have introduced. For instance, assume that the demand for publicly financed education on the part of one social group decreases. Pressures will be generated toward reducing the quantity of publicly supported educational services, and those groups whose demands have not fallen will find themselves subjected to pressures to pay increased school district rates. In such real-world settings, of course, “full trading equilibrium” may never be achieved or even approximated for many reasons. Nonetheless, the analysis of such equilibria is helpful in enabling the competent theorist to identify those political pressures that will arise concerning changes in the size of the budget and in the distribution of the tax burden.
Marginal Prices, Average Prices and Interpersonal Discrimination
There is one difference between the Marshallian model of joint supply and the public-goods model that is of some significance. As presented by Marshall, and as normally discussed, the joint-supply analysis is illustrated with reference to final-product components that are subject to retrade or resale among potential purchasers. Because the jointness arises in the technological process of production itself and not in the absence of divisibility or possibility of exclusion in the consumption of final products, the purchaser of a component of the jointly supplied composite may undertake resale to a third party if this offers opportunity for profit. This characteristic insures that an element of determinacy is present in the Marshallian model which is lacking in the public-goods model. Since resale is possible, prices of final product components must be uniform both over varying quantities of purchase for any one buyer and over separate persons as buyers. This implies that the attainment of a set of equilibrium marginal prices also determines average prices for the products that have been jointly produced. That is to say, the solution depicted at equilibrium determines a unique distribution of the
total costs of production between the purchasers of the separate consumption components, as well as the indicated unique distribution of the marginal costs.
In the public-goods case, the jointness arises only because of the indivisibility or the nonexclusion in consumption. Resale of consumption units among separate demanders is impossible by definition. Therefore, the attainment of equilibrium determines uniquely only
marginal prices confronting the several demanders. This equilibrium may be consistent with almost an infinite number of sharing schemes for the costs over inframarginal units. The prices need not be uniform either over varying quantities or as among separate persons. The average supply price for consumption units need not be equal to marginal price.
In orthodox price theory, the distinction between price discrimination among separate buyers and among separate quantities that may be purchased by a single buyer is noted, but seldom does it warrant particular attention. The reason for the underemphasis is simple; if resale of a good is possible without undue costs, neither type of discrimination can long exist. With public goods, however, resale is wholly impossible, either directly or indirectly. Differences in prices paid by separate persons have been demonstrated to emerge from ordinary motivations in trading. In this case, the distinction between price discrimination over quantity and price discrimination among persons becomes an important one. To clarify this point, consider the sale of a private service rather than a good, say nursing care. It is probable that a firm supplying this service will discriminate among separate buyers; this is standard practice in the pricing of most elements of medical care. Prices tend to be charged in some direct relationship to predicted income levels of the buyers. In addition, the firm may or may not discriminate in its charges to a single buyer over varying quantities of purchase. Its price per day of nursing care may be unchanged whether the single buyer takes one day’s care, one week’s, one month’s or more. Or, perhaps more commonly, the firm may charge a lower price per day for longer periods; it may allow quantity discounts.
When goods and services are made available to a single buyer at differing prices for different quantities, the average price differs from the marginal price at each quantity. The buyer’s choice will be distorted; he will be led by the conditions of the offer to purchase a total quantity either greater or less than that quantity which he would purchase at the same average price but with a uniform, and equal, marginal price. It is this phenomenon of possible price discrimination over quantity to a single buyer that requires discussion in some detail here. As the analysis above has indicated, discrimination in marginal prices among separate demanders or consumers of purely public goods emerges as the outcome of any efficiently organized trading process. In fact, as we have shown, the results in this respect are wholly analogous to Marshall’s theory of joint supply; the use of the very term “price discrimination” in this instance seems itself to be questionable.
Beyond this acknowledged interpersonal differentiation in marginal prices, there remains open the question as to the relation between marginal prices and average prices confronted by the single buyer. What structure will emerge in this respect from the processes of trade? And what will be the effects of this structure on the equilibrium outcome? Methodologically, the analysis here is important. The repeated references to income-effect feedbacks in the earlier discussion may have seemed insignificant. But these feedbacks become of vital importance at this point. What we are confronted with is the appropriateness of such a notion as an individual marginal evaluation schedule or curve for a purely public good.
Individual Demand for a Public Good
Both in this chapter and in the one preceding we have introduced individual demand and/or marginal evaluation curves for a public good without careful definition. This gap must now be filled. The derivation of an individual demand curve or schedule for a private good is straightforward. The potential buyer is confronted, conceptually, with a set of all possible prices, and the maximum quantity that he stands ready to purchase at each price becomes a point in the schedule. In such a derivation, we assume that each offer embodies an equality between average and marginal price. That is to say, the individual demander is assumed to be faced with a series of supply schedules or curves, each of which allows him to vary quantity purchased without modifying average price. Without this critical assumption, no demand schedule for the individual could be derived, even for a purely private good. If, instead of uniform average-marginal prices, the buyer should be confronted with a set of separate “price offers” that contain varying relations between average and marginal price, no single-valued demand relationship between quantity demanded and either average or marginal price would exist. There would be no individual demand curve. Here the individual buyer would be in a position analogous to the monopolistic seller. In the latter case, there is no supply curve that may be derived. The monopolist faces, not a set of demand prices that are uniform over quantity (such as confront the competitive seller) but, instead, a set of demand schedules in the relevant market.
What has all of this to do with the derivation of an individual demand schedule for a purely public good? Can we not, at least conceptually, derive such a schedule in the same way that we derive the demand schedule for a private good? Can we not imagine that we confront the individual with a series of prices, uniform over the quantity range, and ask him what quantity he would prefer at each of these prices? Clearly such a procedure is possible, and we shall employ it in the following section. With public goods, however, this procedure is much more arbitrary than in the comparable private-goods model, and its usage may suggest apparent determinacy where none exists. In the world of private goods, most buyers of final products do face horizontal supply curves. The market economy operates to prevent the emergence of monopolistic quantity discounts or quantity premiums save in rare instances. For this reason an individual demand curve derived in the orthodox manner becomes a relevant tool of analysis. With public goods, by contrast, there are no institutions that prevent price discrimination over quantities, and such quantity differentials may well emerge from an open trading process. To analyze the demand for public goods, therefore, we need something akin to the orthodox demand curve but which possesses more general applicability.
There are three courses of action open. The first is the one already mentioned. We can quite arbitrarily assume that the individual is to be confronted with a set of uniform prices (tax-prices) for a public good. Given this device, a unique relationship between price and quantity demanded can be established. A second method has also been referred to in the simple exchange models of Chapter 2. Discrepancies between average and marginal prices over quantities exert an influence on the behavior of the buyer only because different offers extract from him different amounts of consumer’s (taxpayer’s) surplus. If such real-income effects can be assumed to be negligible or nonexistent, each marginal price must generate a uniquely preferred quantity, regardless of its relationship to average supply price. This procedure might be labeled the Marshallian escape route. In the standard indifference map construction, it amounts to assuming that the individual’s indifference contours have the same slope along any vertical line, provided that we measure private goods (income) along the ordinate and public goods along the abscissa.
This neglect of income-effect feedbacks on individual marginal evaluation is helpful in presenting the elementary theory, but, like the initial method that involves marginal-price uniformity, it remains a device designed for didactic purpose. Income effects must be incorporated in any reasonably sophisticated analysis, and possible departures from marginal-price uniformity must also be allowed. This suggests resort to a third procedure, one that retains most of the pedagogic usefulness of the orthodox demand curve. This involves the introduction of the
marginal evaluation schedule or
marginal evaluation curve, which we have already used without careful definition or discussion.
The basic idea behind this construction is simple. The marginal evaluation schedule indicates the evaluations (in terms of a numeraire) placed on successive units of quantity as seriatim purchases are made by the individual. These evaluations will depend on the average price paid over inframarginal ranges. For every price offer, therefore, a different marginal evaluation schedule may be derived.
Geometrically, a marginal evaluation curve for an individual is derived by taking the slopes of successive indifference curves as these curves intersect a single opportunity curve over varying quantities of the public good. The curve embodies, therefore, the possible effects on the individual’s choice behavior that are exerted by the sacrifice of real income over inframarginal ranges. The rate of required payment is determined by the specific shape of the opportunity curve over the relevant quantity range. The successive slopes of the opportunity curve provide a schedule of marginal prices, and this schedule can take any form. Marginal price may be equal to, greater than, or less than, average price through all or any part of the quantity range.
 |
| Figure 3.2 |
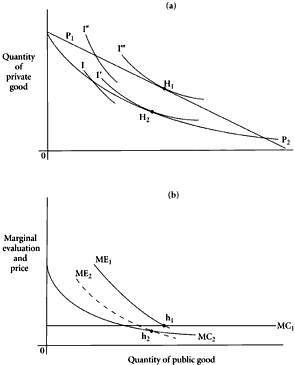
The deficiency of the marginal evaluation schedule or curve as an analytical tool lies in its dependence on the uniqueness of the opportunity curve or offer schedule. For each price offer represented by a single curve there can be derived a different marginal evaluation curve or schedule. This is illustrated in Figure 3.2(a)-(b). Assume that a person is faced with a standard uniform price offer represented geometrically by the linear opportunity line,
P1, in Figure 3.2(a). Given this offer, we derive a marginal evaluation curve by tracing the slopes of the successive indifference curves as they cut this opportunity line. Such a curve is drawn in Figure 3.2(b) and is labeled,
ME1. Marginal cost or marginal supply price is simply the slope of
P1, which in this case is constant over quantity. The curve of marginal cost is shown as
MC1. Equilibrium is shown at
H1 and
h1 on the two parts of Figure 3.2.
Note that the marginal evaluation curve,
ME1,
does not tell us anything at all about how much the person would purchase at any other supply price or price offer. It is not, therefore, analogous to the demand curve in this general sense. The construction does enable us, with facsimiles of the Marshallian tools, to depict the characteristics of the final equilibrium position for the individual. Only in this sense does the marginal evaluation construction resemble that of the orthodox demand curve in the absence of further qualifying assumptions.
If the individual whose choice is examined should be confronted with an alternative supply price offer or opportunity, a different marginal evaluation curve and a different marginal supply price must be derived. One such alternative offer is shown as curve
P2, in Figure 3.2(a). Here the buyer is faced with an opportunity to purchase the good at a quantity discount. Marginal price falls below average price throughout the quantity range. In the same way as before, we can construct a marginal evaluation curve by plotting the slopes of the successive indifference curves as they cut
P2. This curve is drawn as
ME2 in Figure 3.2(b). The marginal cost or marginal supply price curve now becomes
MC2. Equilibrium is again shown at
H2 and
h2. Note that the marginal evaluation curve cannot be employed “to locate” the equilibrium position, given changing offers or supply price. To use the curve in this fashion would involve circular reasoning. The construction does, however, present a picture of equilibrium, once attained.
Determinacy Restored by Marginal-Price Uniformity
The discussion in the preceding section may seem unduly tedious, but it is fundamental to an understanding of the theory of public goods. At equilibrium, the marginal rates of substitution between the public good and the numeraire private good, summed over all persons in the group, must equal the marginal cost of supplying the public good, again expressed in units of the numeraire. This statement of the necessary marginal conditions for equilibrium in a world that contains a public good is fully general, and holds without qualification. It is erroneous, however, to infer from this statement of the necessary marginal conditions that an external observer can locate or find the equilibrium supply of public goods by summing individual marginal evaluation curves or schedules and comparing these sums with observed marginal costs. In geometric terms, it is erroneous to sum vertically the separate individual marginal evaluation schedules and then to locate the equilibrium or optimal supply of the public good at the point where the aggregate curve cuts the curve of marginal cost.
 |
| Figure 3.3 |
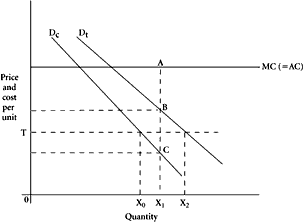
This conclusion need not imply that we dispense with the simple Marshallian geometry. It does suggest that we handle the tools properly and with due caution. Does there exist a methodologically legitimate means of utilizing the familiar constructions to find equilibrium in the supply of public goods, given individuals’ utility functions and the costs of the good to the community of persons? As is indicated above, in the general case where marginal-price uniformity cannot be assumed present and where income effects cannot be neglected, there is no such means. If used with proper caution, however, the arbitrary convention regarding marginal-price uniformity revitalizes the geometrical construction. Refer now to Figure 3.3. As before, assume that the public good is available to the community at constant marginal cost, indicated by the curve
MC. We adopt the convention that tax-prices per unit of the good are to be uniform over various quantities for each person, although, of course, these need not be uniform as among separate persons. This step allows us to derive demand curves for the public good in the orthodox fashion. Conceptually, we simply confront each individual with the opportunity to “purchase” or to “vote for” a most preferred quantity at each price (marginal = average). These curves for Tizio and Caio are labeled
D
t and
D
c in Figure 3.3. (Note specifically that these are
not marginal evaluation curves.) The information contained in these demand curves and the cost curve allows us to determine uniquely the efficient supply of the public good and the equilibrium set of marginal tax-prices that each person must confront. 0
X1 represents this quantity, and
BX and
CX the equilibrium marginal-average tax-prices. The determinacy here is introduced through our assumption as to the uniformity in tax-price over quantity. This assumption or convention, which is admittedly an arbitrary even if a reasonable one, allows income effects to be included in the model, but it does so only by guaranteeing one particular division of the gains-from-trade that are secured in producing the public good.
This particular sharing scheme is directly analogous to that which ordinary trading processes generate in the private-goods world where resale possibilities exist. Since these do not exist, by definition, in the public-goods world, such a sharing scheme must be arbitrarily introduced or “constitutionally” agreed upon by all participants. Once accepted, and given a set of initial resource endowments, and given the utility and cost functions, equilibrium is uniquely determined.
The manner in which our two-person group could grope its way toward a final equilibrium adjustment under this convention of marginal-price uniformity can be shown readily. Suppose that the two traders initially agree that tax-prices for units of the public good to be confronted by each person are to remain uniform over quantities. Suppose further that each person recognizes the publicness of the good at the outset, but that no strategic behavior takes place. This latter assumption is useful in that we want to utilize the small-number model as an analogue for large-number situations where strictly strategic behavior may be absent. Tizio takes it upon himself to propose various sharing schemes, all within the price-uniformity convention. Initially, he proposes that each person should pay one-half of the marginal cost per unit of the public good, represented on Figure 3.3 by the tax-price 0
T. At this level, Caio will agree to finance only a quantity, 0
X0, whereas Tizio will desire to finance an amount, 0
X2. Since the two persons must agree on a single quantity, the initial proposal fails and Tizio then makes an alternative proposal, increasing his own tax-price and,
pari passu, reducing that confronting Caio. He will proceed to modify the offer in this fashion until Caio agrees on the same desired quantity that he himself prefers. And, as the construction indicates, only the amount, 0
X1, fits this requirement under the price-uniformity constraint that we have imposed.
In utilizing this convention or assumption as a means of shoring up the usefulness of Marshallian geometry, we are implicitly selecting the final position on the Pareto welfare surface. Other positions of final equilibrium embodying different distributions of the taxpayers’ surplus may be equally relevant in any given real-world situation, and no “efficiency” attributes characterize the arbitrary position that the convention produces. There is, nonetheless, something more than mere analytical convenience in the price-uniformity convention. Uniformity in tax-price over quantity is characteristic of any tax-sharing scheme that maintains constant share progressivity. Since many major revenue producers in real-world fiscal systems meet this requirement, the model warrants analytical distinction, provided that its limitations are kept in mind.
Bibliographical Appendix
The separate demanders of a purely public good must be charged different marginal prices if the necessary conditions for efficiency are attained. This has been recognized, with varying degrees of precision, by almost all contributors to the voluntary exchange theory of public finance from Sax down to the present day. The requirement is implicit in Wicksell’s early treatise. It becomes quite explicit in Lindahl, and it is also stressed in Howard Bowen’s early modern formulation [“The Interpretation of Voting in the Allocation of Resources,”
Quarterly Journal of Economics, LVIII (November 1943), 27-48]. It is contained in both Musgrave’s and Samuelson’s statements of the theory, but it is not emphasized. In his valuable survey paper, J. G. Head states the requirement for differential marginal prices concisely [“Public Goods and Public Policy,”
Public Finance, XVII (No. 3, 1962), 197-221]. Essentially the same problem arises in the theory of public-utility pricing under joint costs. An early and important statement was made by Donald H. Wallace [“Joint and Overhead Costs and Railway Rate Policy,”
Quarterly Journal of Economics, XLVIII (August 1934), 583-619]. Recent contributions have concentrated on peak-load adjustments and have stressed the necessity of differing marginal prices in separate periods; these include papers by H. S. Houthakker, Peter Steiner, Jack Hirschleifer, and Oliver Williamson [Houthakker, “Electricity Tariffs in Theory and Practice,”
Economic Journal, LXI (March 1951), 1-25; Steiner, “Peak Loads and Efficient Pricing,”
Quarterly Journal of Economics, LXXI (November 1957), 585-610; Hirschleifer, “Peak Loads and Efficient Pricing: Comment,”
Quarterly Journal of Economics, LXXII (August 1958), 451-62; Williamson, “Peak-Load Pricing and Optimal Capacity Under Indivisibility Constraints,”
American Economic Review, LVI (September 1966), 810-27].
In the monograph cited previously, Milton Z. Kafoglis noted the distinction between those external economies that arise from the act of producing a good or service for common consumption and those that arise from the act of consuming as such [
Welfare Economics and Subsidy Programs, University of Florida Monographs in Social Science, No. 11, Summer 1961].
The joint-supply characteristic of public goods has been specifically treated, in general terms, by Carl Shoup [“Public Goods and Joint Production,”
Rivista internazionale di scienze economiche e commerciali, XII (1965), 254-64]. In the valuable survey paper cited in the preceding paragraph, Head has also developed this aspect of the theory. Geometrical models based on Marshallian joint-supply analysis were extended to apply to an impure public good in a paper by James M. Buchanan and Milton Z. Kafoglis [“A Note on Public Goods Supply,”
American Economic Review, LIII (June 1963), 403-14]. The distinction between units of production and units of consumption was discussed in my 1966 paper [“Joint Supply, Externality, and Optimality,”
Economica, XXXIII (November 1966), 404-15].
The difficulties raised by income-effect feedbacks on allocative outcomes in public-goods models were noted by Paul A. Samuelson in his two basic papers [“The Pure Theory of Public Expenditure,”
Review of Economics and Statistics, XXXVI (November 1954), 387-89; “Diagrammatic Exposition of a Theory of Public Expenditure,”
Review of Economics and Statistics, XXXVII (November 1955), 350-56]. The implications of this relationship were emphasized by Robert H. Strotz in his note [“Two Propositions Related to Public Goods,”
Review of Economics and Statistics, XL (November 1958), 329-31]. The importance of the feedback income effects on allocative solutions in the related peak-load pricing problem was the main point of my comment [“Peak Loads and Efficient Pricing: Comment,”
Quarterly Journal of Economics, LXXX (August 1966), 563-71]. André Gabor provided a more rigorous analysis of this application [“Further Comment,”
Quarterly Journal of Economics, LXXX (August 1966), 512-80].
The derivation of marginal evaluation curves was discussed by J. R. Hicks in an early paper [“The Four Consumer Surpluses,”
Review of Economic Studies, XI (1943), 31-42]. In a 1952 paper, I developed this construction in a particular application [“The Theory of Monopolistic Quantity Discounts,”
Review of Economic Studies, XX (1952-53), 199-208].

