The Demand and Supply of Public Goods

Many Private Goods, Many Persons:

The “Free-Rider” Problem

The assumptions of our initial models have been progressively relaxed, and the theory of public goods has become more general in the process. The generalization remains incomplete in essential respects, however, due to the two-person, two-good limitation. Extension to the
n-person,
n-good cases must now be introduced. Should these final steps prove impossible, some of the earlier simplifications would be of negative rather than positive explanatory value.

From One to
N Private Goods

One stage of this remaining generalization is simple. No difficulties arise in shifting our attention from a world where
one private good and
one public good exist to a world where there are
n private goods and
one public good. This is the model within which much of the theoretical discussion of public goods demand-supply has taken place. The results are equivalent to those reached in the simplified two-good model. All that is required here is the selection of one from among the
n private goods as a
numeraire, that is, as a money commodity. Once this is done the model reduces to the two-good case as before, with the numeraire becoming a common denominator for all private goods. Actual and potential exchanges can be treated as transfers in the numeraire. In this respect, the “market” for the single public good is not different from that for any single selected nonnumeraire private good. All trades reduce to two-good dimensions. This acknowledged function of the money commodity has been emphasized for its efficiency-promoting results. The costs of exchange in a money economy are drastically lower than those in any comparable barter system. The dimensional aspect here has not, however, been so fully appreciated for its facilitation of elementary theorizing about the market processes. The use of money allows the economist, who has normally been concerned almost exclusively with private-goods exchange, to possess a “magic number,” two, despite all of his sophisticated models covering many commodities.

From One to Many Public Goods

So long as there is one purely private good to serve as a numeraire, no problem arises in generalizing the model to include any number of public goods. Each of the latter can be treated separately and “trade” in this good and the numeraire can be discussed in the same terms as before. Complexities emerge when complementarity and substitutability relationships among public goods are strong, or when institutional arrangements for provision (e.g., general-fund budgeting) force joint considerations. These complexities need not be disturbing for elementary analysis, however, and the standard professional tools of economics can be employed.

The model cannot be generalized to cover the case where
all goods are public. Here no numeraire private good is available to reduce the analytics to our magic two dimensions, and trade becomes much more complex, both in reality and in analysis. We must resort to something like a generalized barter model. Such a model does have relevance to certain real-world problems, notably those encountered when the theory is applied to certain political-choice situations. This particular extension will be developed separately in Chapter 6. At this point, our analysis will be limited to models that contain at least one numeraire private good.

From Two to Many Persons

The major part of this chapter concerns the dropping of the other half of the restriction on models introduced to this point, that which is imposed on the number of persons or potential trading entities. Here, once again, no problem arises in analyzing trade in private goods, at least no problem that is not thoroughly familiar to the trained economist. As we know, shifting from two-person to
n-person models facilitates analysis in many respects. In two-person exchange, neither trader confronts alternatives outside the exchange nexus. Each person finds it advantageous to behave strategically, to bargain, since the terms of trade as well as the extent of trade are determined internally to the exchange process. If, however, there exist alternative buyers and sellers, the terms of trade tend to be imposed externally on both parties to any specific exchange. These terms are fixed by all participants indirectly in a large-number market process, and they exogenously set the respective shares in the total gains derived by two traders in any single exchange. Their own decisions, within the narrow confines of this exchange, reduce to agreeing on quantities to be transferred on these given terms. The necessary conditions for full trading equilibrium are identical in
n-person and in two-person models. But because all traders adjust to common price ratios the
n-person model is more determinate.

Figure 5.1

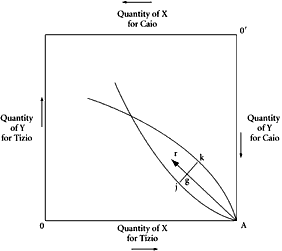
This distinction is illustrated in Figure 5.1, which is again the familiar Edgeworth-box diagram. Under two-person trade in isolation, the contract locus,
jk, represents the set of all possible final equilibrium positions, given
A as the initial point. At each position on this locus, the necessary marginal equalities hold; all gains-from-trade are exhausted. In shifting from
A toward the contract locus, each trader is motivated to bargain, to behave strategically, in order to secure more favorable distribution of the available spoils. In an
n-person situation the same two traders would tend to move swiftly along the single ray,
r, to a unique point,
g, on the contract locus, the slope of this ray being the price ratio between the two goods. This price is set externally, and, once set, it determines uniquely the solution to the “bargaining game” in which these two players would engage if they were isolated. The price ratio exerts this stabilizing and efficiency-generating influence because it represents the terms upon which each trader may exchange with outsiders, that is with alternative sellers-buyers. Clearly, neither trader will ordinarily give his direct opposite number much better terms than he can secure from others. Most of the structure of neoclassical price theory consists of inferential predictions about characteristics of rays along which exchanges take place; that is, with predictions about prices that will come to be established through the interplay of all the demand-supply elements in
n-person,
n-commodity markets.

Perfect Competition

The extension of the model analyzing trade in private goods from two persons to many persons has been oversimplified in the above summary. Full determinateness in the model emerges only when all of the requirements for perfect competition are satisfied. Much of modern analysis assumes at the outset that competition is perfect and then proceeds to derive inferential predictions about the characteristics of equilibrium. Interesting and important questions concerning the path toward final trading equilibrium have been relatively neglected. While there is no doubt but that this methodological procedure has facilitated analysis in many respects, its value in contributing to our understanding of the way market institutions may be predicted to function seems questionable. A more fruitful approach is one in which competitive organization
emerges as a result of the interaction of demanders and suppliers in markets, instead of being superimposed, as it were, by assumption. This latter approach is necessarily more cumbersome and complex, and all ideas about uniqueness of solution must be jettisoned. There exist many paths toward final equilibrium; there is some scope for bargaining behavior in almost every trading situation. Prices come to be established in a process of moving toward an ever-changing equilibrium; they are not “solved for,” computer-style, exogenous of behavior in markets and then subsequently “announced.”

This approach concentrates on exchange as such. And even in a world where many persons mutually trade among themselves in many private goods, all exchange is still two-sided. The economist can still call up his magic number, two. In each exchange, there is one selling unit and one buying unit; each trade is bilateral. In this sense, usage of the term “multilateral” by economists is often misleading. The emergence of a money commodity, a numeraire, allows the whole trading process, however many persons and many goods it may involve, to be factored down, so to speak, into an intersecting set of two-person, two-good exchanges.

The limitation on strategic behavior, on bargaining, is imposed by the availability of alternatives, actual and potential. To the extent that effective alternatives exist, the prospects of productive returns from investment in strategy are reduced. In the extreme, expected returns do not equal costs even at the zero margin. Each of us faces this situation in standard American retail markets. We confront single sellers, but we do not normally find it worthwhile to bargain over prices. The seller, because he has alternative buyers, will not readily respond to below-list offers. However, because buyers also have access to alternative sellers, the single seller cannot readily put his own prices above those charged by others. Alternatives impose external limits on the two-person, two-good trade in private goods, and the effectiveness of these alternatives measures the efficiency of the market structure.

The purpose of all this is not to present a discourse on the theory of markets. The point emphasized is that so long as we restrict analysis to trade in private goods, we do not effectively change dimensions in shifting from the grossly simplified two-person, two-commodity model to one that contains many persons and many goods. Such a shift adds determinateness to the results because the terms of trade are affected by potential as well as actual exchange. Since each trader can independently adjust his quantities of private goods, as demander or supplier, there is no necessity of introducing
n-party exchange models explicitly.

N Persons and “Trade” in a Single Public Good

This characteristic of independent quantity adjustment greatly facilitates both trade and theorizing about trade. When a public good is introduced, parties can no longer adjust quantities independently. As the analysis of earlier chapters has shown, we can define the characteristics of trading equilibrium, even here, so long as we stay in the two-person model. As we add more parties to such a model, however, and as we shift from the two-person toward an
n-person case, we do not secure the same efficiency as in the world where trade is limited exclusively to private goods. With public-goods exchange,
all relevant parties must be brought directly into the contract. The economist’s magic number fails, and no amount of sophisticated theorizing can really factor down the trading process into a set of intersecting two-party exchanges. Genuine
n-person trade must be analyzed for the first time, and the “solution” must reflect agreement among all of the
n trading partners.

The problem may be discussed in terms of agreement. Return to trade in purely private goods. This trade requires explicit agreement between only two persons in each exchange, a buyer and a seller, along with the implicit agreement or acquiescence on the part of the other
n-2 members of the group. Private goods trade involves
implicit unanimity, in the sense that parties external to each particular exchange allow the two traders involved to remain undisturbed in their dealings. Institutional arrangements are, of course, designed to prevent such interference by external parties, but these institutions themselves emerge from a recognition of the underlying realities of most exchanges. Unless such implicit unanimity is present, external parties can prevent any proposed exchange by offering more attractive terms to one of the two traders. It is this particular characteristic of competitive economic order that allows it to satisfy the familiar necessary marginal conditions for Pareto optimality. Trade in private goods will proceed so long as mutual gains remain unexploited, and so long as this requirement of implicit unanimity is met. Implicit unanimity is not imposed, however, on private-goods trade; it is a characteristic of such trade.

In our previous analysis of Tizio-Caio trades, the motivation for agreement on supplying the public good was shown to be equivalent to that for engaging in ordinary private-goods trade. Mutual gains can be secured through mutual agreement. The same motivation holds when we add more persons to the model; unexploited gains-from-trade will be present so long as persons who place any positive marginal evaluation on the public good remain outside the range of agreement. To show this in a three-person case, let us add Sempronio to the Tizio-Caio illustration. Suppose that Sempronio desires to migrate to the island, and that he, like the others, will share equally in the benefits of any mosquito repelling activity. Tizio and Caio will not be willing to allow Sempronio to join them unless he contributes some share in the costs of this public good, either through direct production on his own account or indirectly through transfers to them of private goods. Sempronio will, presumably, be prepared to make some contribution toward this end. He cannot, however, simply engage in ordinary exchange with either Tizio or Caio. The two-party agreement between Tizio and Caio on the quantity of public good to be jointly supplied must now become a genuine three-party agreement in a direct and explicit sense. Each person will now have to consider his own contribution in relation to each of the other two persons and to both combined. The extension to four, five and on to
n persons similarly will require further inclusion in the range of
explicit agreement. Such agreement is necessary in all instances where decisions are made on the amount of public good to be supplied jointly for all relevant members of the group.

The most obvious inference to be drawn from this preliminary discussion concerns the predicted increase in the costs of reaching agreement as the number of parties in contract expands. Two-party bargains may be difficult enough, especially when the gains-from-trade are large. Three-party bargains are probably proportionately more difficult still to arrange. As the size of the inclusive group becomes large, explicit agreement among all members may actually become almost prohibitively costly. It is essential to understand precisely why this is true. Herein lies the explanation of the failure of market-like or exchange organization to function effectively in supplying public goods that jointly supply large groups. Also here is provided the explanation for the emergence of indirect trade via the mechanism of collective-coercive arrangements.

Strictly Strategic Behavior—The Small-Number Case

When
all members of a group must reach agreement, and there is no external contact with others outside the group, there are no external limitations on the terms of trade among these members. This holds for two-person, few-person and many-person groups. It is necessary, however, to distinguish carefully the behavior of the individual participant in a small-number setting and that of the same individual in a large-number setting. Rational behavior will be quite different in these two cases, despite the presence of the same general sort of mutual interdependence. In small-group situations, each potential trader is motivated to behave strategically, to bargain, in an attempt to secure for himself differentially favorable terms. At the same time, he will also seek to promote general agreement so as to secure the advantages of the acknowledged mutual gains. Here the trader expects through his own action to modify the behavior of fellow traders in the group. He will try to predict as best he can the response of these others to his own action, and he will then select that combination of action and predicted response that maximizes his expected utility. He is in an acknowledged gaming situation. He may deliberately resort to strategic “antisocial” behavior even though he recognizes that mutual gains can be secured from cooperative behavior. It is in this small-number model that strictly strategic behavior on the part of the participant becomes fully rational. Here the individual will find it to his advantage to conceal his true preferences and to give false signals about those preferences to his opponents-partners.

This small-number case has been exhaustively analyzed by game theorists, although wholly satisfying results have not extended beyond the level of two-person, constant-sum games. The several approaches need not be elaborated here since these models are
not those most appropriate for analyzing
n-person “trades” in public goods. Normally, political groups are organized so as to include many persons. Our analysis must, therefore, be confined primarily to the large-number case.

General Interdependence—The Large-Number Case

The individual, as a member of a large group characterized by general interdependence among all of its members, will not expect to influence the behavior of other individuals through his own actions. He will not behave strategically; he will not bargain; he will not “game.” Instead, he will simply adjust his own behavior to the behavior of “others,” taken as a composite unit without the anticipation that their behavior may change. He accepts the totality of others’ action as a parameter for his own decisions, as a part of his environment, a part of nature, so to speak, and he does not consider this subject to variation as a result of his own behavior, directly or indirectly.

A familiar reference to orthodox price theory will make the distinction between the small-number and the large-number case clear. In a duopoly or oligopoly situation, the rational firm tries to predict the response of its rivals to its own actions. In a competitive setting, by contrast, the firm accepts the behavior of its “rivals,” as a datum, and simply reacts to its environment. The underlying interdependence through the market is the same in both instances, but the difference in numbers generates basic differences in the behavior patterns of rational decision makers. In the large-number model, the individual considers the influence of his own action, relative to the totality of action generated by the group within which he operates to be so small as not to affect at all the aggregative results. Hence, he reasons, and correctly, that he had best ignore altogether the reactions of others (separately or as a subgroup) to his own possible “antisocial” behavior.

The psychology of behavior differs in the two situations. In small-group interaction, the individual recognizes interdependence in a specifically personalized sense. He will be directly conscious of rivalry; he will (in situations where the numbers exceed two) be motivated to form coalitions. He will recognize the productivity of joint action with one or more of his fellows.
Vis-à-vis each other person in the group, the individual will sense a relationship of both competition and cooperation. All of this disappears in the large-number situation. The individual may fully acknowledge the mutual interdependence among all members at some logical, analytical level of discourse. But he will not find it productive to seek out and form coalitions with his fellows to the extent evidenced in the small-number case. He will not consider himself either competing or cooperating with other members of the group. There is no personalized relationship of interdependence here, no scope for bargaining to obtain favorable terms of trade since, for each person, these terms are exogenously fixed. This removal of bargaining opportunities has its obverse, however, in that no trades will be arranged either. The small-number case provides the individual with motivation both to initiate trade and to bargain over terms. The effective large-number case, where interdependence is general and cannot be factored down, tends to eliminate both trading and bargaining behavior.

In the large-number setting, individuals find it rational to act independently, despite the fact that the composite result of individual and independent action is nonoptimal for each and every person in the group, and this may well be recognized as such.

Public-Goods Supply and “Free Riders”

When the large-number dilemma summarized above exists, the natural processes of trade, the emergence of market-like institutions, cannot be predicted to generate shifts toward optimality. Gains from
n-person trade or agreement are clearly present, and these potentialities may be universally recognized. But market-like arrangements cannot readily materialize due to the absence of notable gains from two-person or small-number exchanges.

In such situations, individuals will suggest
n-person “rules” or “arrangements” aimed explicitly at reducing or eliminating the inefficiencies generated by independent behavior. In a very broad sense, agreements on such rules can also be classified as “trades.” It may prove almost impossible, however, to secure agreement among a large number of persons, and to enforce such agreements as are made. The reason for this lies in the “free-rider” position in which each individual finds himself. While he may recognize that similar independent behavior on the part of everyone produces undesirable results, it is not to his own interest to enter voluntarily into an agreement since, for him, optimal results can be attained by allowing others to supply the public good to the maximum extent while he enjoys a “free ride”; that is, secures the benefits without contributing toward the costs. Even if an individual should enter into such a cost-sharing agreement, he will have a strong incentive to break his own contract, to chisel on the agreed terms.

It is worth noting that there are no personal elements in the individual’s calculus of decision here, and, for this reason, the “free-rider” terminology so often used in public-goods theory is itself somewhat misleading. The individual is caught in a dilemma by the nature of his situation; he has no sensation of securing benefits at the expense of others in any personal manner. And to the extent that all persons act similarly, no one does secure such benefits. Free rider, literally interpreted, more closely describes the small-number model, in which the individual does compete explicitly with others in a personal sense. Here, “let George do it” means just that, with George fully identified. But the small-number model is not appropriate for analyzing the theory of public goods. In the relevant large-number setting, the individual does not really say to himself, “let George do it”; he simply treats others as a part of nature. The “prisoners’ dilemma,” which has been analyzed at length in game theory, is more descriptive of the large-number behavioral setting, but, even here, this dilemma has normally been developed in two-person models. In such models, nonoptimality arises because of the mutual distrust and noncommunication between the prisoners, which are once again personal relationships. In the large-number or
n-person dilemma, the failure to attain desirable results through independent action is analytically equivalent to the orthodox prisoners’ dilemma, but without the personal overtones. Full communication among all persons in a large-number dilemma will still not remove the inefficiency in results.

The organization and enforcement of efficient institutional arrangements will rarely be possible unless
all persons are somehow brought into potential agreement. The alternative of remaining outside the agreement, or remaining a free rider, must be effectively eliminated before the individual can appropriately weigh the comparative advantages of independent behavior on the one hand and cooperative action on the other. It is because they facilitate the elimination of this free-rider alternative that coercive arrangements, governmental in nature, tend to emerge from the preferences of individuals themselves, at least on some conceptual level of constitution-making. Once the possibility or opportunity of behaving as a free rider is removed from an individual’s range of effective choice, he can then select among the remaining alternatives on more meaningful terms of comparative efficiency, at least in an ideal sense. His behavior under these more restricted conditions will be discussed more fully later in the chapter. Before this, however, it will be useful to show why, in the large-number case, the individual will not contribute voluntarily to the costs of public goods, at least not in an amount sufficiently large to generate optimal levels of provision. The analysis in the following section is redundant in one sense, but, as suggested earlier, varied iteration can serve pedagogic purpose.

A Probabilistic Approach to the Free Rider’s Choice

Consider first a community of 1000 persons in which it is widely known that a fixed-facility purely public good, if constructed, will yield benefits valued at $10 per person, or $10,000 in total. It is also widely known that the facility can be constructed for $5000.

Each individual examines his choice alternatives, which he considers as: (1) contribute a share in the joint cost of the undertaking, or (2) contribute nothing. How will he rank these alternatives? If he predicts that others in the group will contribute an amount sufficient to finance the facility, he can obviously gain from not contributing. If he predicts that others in the group will not contribute, he gains nothing by contributing himself because of the indivisibility of the benefits. In view of the large-number setting, the individual does not predict that his own behavior can influence others in the group. There will be no difference in his predictions as to the aggregate behavior of others whether or not he contributes a share of his own. In this sort of situation, regardless of how the individual estimates the behavior of others, he must always rationally choose the free-rider alternative. Since all individuals will tend to act similarly, the facility will not be constructed from proceeds of wholly voluntary contributions of potential beneficiaries.

Figure 5.2

This situation may be illustrated in the simple matrix shown as Figure 5.2. Values to the individual under the different combinations are taken from the numerical example. The terms in brackets represent probabilities assigned to each of the possible behavior patterns of others. The important thing to note is that these probabilities do not change from one row to the other. This being the case, any set of probability coefficients will give the same result. The highest expected value will always be assigned to the row labeled “Not Contribute.”

Figure 5.3

This situation, relevant to the large-number setting, may be sharply contrasted with that present in a small-number case. Under the same general conditions as before, assume now that the community contains 10 persons. Each person now anticipates a total benefit of $1000 and a
pro rata cost share of $500. He will face the same alternatives as before; he can contribute or he can refrain from contributing. However, in this small-number setting, where personal interaction is recognized, the individual may consider that his own action will exert some influence on the behavior of others in the group. If he contributes nothing, he may assess the probability of noncooperation on the part of others higher than if he contributes some share. This change alone may be sufficient, on rational grounds, to cause him to contribute. In terms of the small-number example introduced above, the situation is summarized in Figure 5.3. Note that the probability assignments do vary from row to row; the individual predicts that his own behavior will influence that of others. This is why, as shown in this example, the expected value is higher when the individual contributes than when he does not. Whether or not this result will be forthcoming depends, of course, on the specific assignment of probabilities. The individual may consider that his own action in contribution will lower, not increase, the probability of others’ making contributions of their own. In this case, the shift in probabilities between rows would be the reverse of that indicated in Figure 5.3. This situation is illustrated in Figure 5.4, which indicates that the individual attains a higher expected value by not making than by making voluntary contribution to the cost of the public-goods facility. Here the individual is quite specifically acting like a free rider. He anticipates that others will offset or compensate for his own antisocial behavior. Whether or not conditions are like those shown in Figure 5.3 or Figure 5.4 will depend, in part, on the power of sanction that the group exerts over the individual. Since the whole analysis applies only for
small groups, the interaction is likely to be personal, and the possibility of excluding genuine nonconformists will normally be present. This suggests that the situation depicted in Figure 5.3 is more likely to occur than that depicted in Figure 5.4.

Figure 5.4

In both the large-number and the small-number examples, we have assumed a certain lumpiness or indivisibility in the public-goods facility. This insures that no production will be forthcoming under wholly voluntary behavior in the large-number case, and perhaps none in the small-number case. In order to make the analysis fully comparable to the models introduced earlier, this assumption of lumpiness must be dropped. If we now assume that the public good can be produced in fully divisible units, some quantity may be forthcoming even in the large-number setting. An independent-adjustment equilibrium will be established with some positive production even if this remains small relative to the Pareto-optimal output under normal circumstances.

The probabilistic approach makes the distinction between individual behavior in the large-number and the small-number setting clear. There is, of course, no
a priori means of determining just what size a group must be in order to bring about the basic shift in any individual’s behavior pattern. This will vary from one individual to another, even for members of the same group. The critical limit is imposed by the personal relationship that the individual feels with his fellows in negotiation. During periods of extreme stress, such as was apparently evidenced by the British during World War II, behavior characteristic of small groups may have extended over almost the whole population. In other situations, when such cohesive forces do not exist, and when commonly shared goals are not apparent, individuals may behave as they would in large groups, even for quite limited community actions. Variations in custom, tradition, in ethical standards; all these serve to shift the critical limits between small-group and large-group behavior. This has, of course, been recognized by economists. The number of firms necessary to insure genuine competition is acknowledged to vary widely with many relevant determining variables.

Wicksell’s Unanimity Rule

When there exists general public-goods interdependence among many persons, the independent behavior of separate individuals will not generate shifts toward Pareto-efficient outcomes. The rules for behavior must somehow be modified. Knut Wicksell was the first scholar to recognize this, and he proposed specific changes in the setting within which individual choices are made. The free-rider motivation is eliminated only when the individual is made aware that this own choice among alternatives
does affect, and in some positive and measurable sense, the outcomes for
others in the group, even if the membership is large. To accomplish this, Wicksell proposed that group decisions on public-goods supply be made
unanimously.

Note precisely what the requirement of unanimity does. Knowing that
all persons in the group must agree before a decision becomes effective, the individual now chooses an outcome, not only for himself, but also for each and all of his fellows. He is confronted with the stark fact that remaining a free rider is impossible. He cannot behave independent of the group. If he refuses to agree to a specific proposal, he cannot expect others to proceed with its implementation. His refusal to accept a proffered scheme for the whole group means that this particular scheme will not come into being; he cannot expect the benefits without their corresponding costs.

In its practical effect on the individual’s behavior, the unanimity rule converts the large-number case into a small-number case. Under this requirement, the effective size of the group is reduced to two parties; the individual considers himself to be trading with “all others” as a unit. The free rider is wholly eliminated, but the difficulties that arise in the small-number case are reintroduced to an extent. There is scope for bargaining, for strategic behavior, for gaming, in the explicit sense, behavior that is wholly missing from the
n-person situation under independent action. Despite these problems, strong motivation exists for the individual to engage in trade, and some approach to the Paretian efficiency frontier may be predicted to take place.

Let us examine somewhat more carefully the situation of the individual under an effective rule of unanimity. A proposal is made, let us say, to supply
X units of a public good at a total tax charge of
Y dollars on each person. Assume for the moment that the benefits of this proposed quantity exceed the costs for the reference person whose calculus we are considering. He will secure some net taxpayer’s surplus if the proposal is adopted by the group. He may, however, vote against the proposal under certain conditions. He will do so if he anticipates that, after defeat of the proposal (which his own vote can insure), a different proposal will be presented that will yield him higher net benefits and which stands some chance of being adopted. Each person is, in a sense, involved in an ordinary two-party bargaining game with all others, whom he considers as a unit.

Important elements of the large-number case remain in this situation, however, elements that reduce substantially the motivation for strictly strategic behavior. Shifts toward the Pareto frontier are, therefore, more predictable here than in genuine two-party bargaining situations. To an extent, the individual must consider any proposal to be exogenously presented. He will not attribute the proposal to a specific bargaining party, as a person, since the party he confronts exists only in the “all others” form. The individual will not predict that his own strategy will exert much, if any, influence on the behavior of his “trading partner.” He remains, in this sense, in the large-number case. By refusing to accept the terms implicit in a proposal, he will not consider himself to be influencing substantially the terms of subsequent proposals that will be put forward. He will not think that he is necessarily empowered, through his refusal to accept a proposal, to suggest alternative ones that provide him with more favorable terms. He may think of proposals as being advanced almost at random with the order quite independent of his own actions. There will always remain the probability that a proposal subsequently introduced would be more favorable than the one under consideration, but this probability will not be significantly changed by his own refusal to accept any particular proposal that is presented.

In view of these characteristics of the situation, the individual will tend to vote favorably on proposals that provide him with net benefits, and which also allocate total costs among all persons in a manner that he considers to be “fair,” “just” or “equitable.” These essentially ethical considerations become important for the individual’s own calculus of choice here because they influence his own predictions as to the success or failure of subsequent proposals. Assume, for example, that a collective group is composed of individuals roughly equivalent in economic position. A proposal is advanced to finance, from the proceeds of a head tax, a public good known to provide general benefits. Assume further that each person will secure some net benefits. In this situation, an individual is likely to vote for the proposal. If he places all others in his own position, he will recognize that symmetry or fairness in the distribution of costs is a relevant factor in his choice.

Note that the behavior here is not the same as that discussed under the generalization principle in ethics. This latter principle states that an individual should act favorably on a proposal if he considers the results to be favorable should all others act similarly. What the unanimity requirement does is to force all others to act, if not similarly, at least as laid down in the specifics of the proposal presented. The distribution of costs among all persons is specified in the proposition. The generalization principle in ethics, as a norm for voluntary behavior, fails in large-number groups for precisely free-rider reasons. Wicksell’s emendation takes the form of a general rule, to be imposed on everyone, that the individual may rationally support.

While the elements of the large-number case that remain under an effective unanimity rule tend to make the average or representative individual choose among alternatives in some nonstrategic sense, such behavior cannot be generalized to
all members of a large group. However, the nature of the unanimity rule is such that group decisions are impossible unless
all persons agree. A single negative vote blocks a proposal, even if all others in the group approve it. To the extent that participants fully appreciate their own individual blocking power, some negative votes could be predicted with almost any conceivable proposal that might be put forward, regardless of the net benefits provided to each person and regardless of symmetry or fairness properties. Practically speaking, the rule of unanimity would result in few, if any, decisions being made.

Again Wicksell recognized this, and he modified his scheme to allow for some departure from complete unanimity, for which he substituted “relative unanimity,” relatively unanimous approval, by which he seems to have meant some five-sixths of the total membership. Note precisely what this qualification of the rule accomplishes. So long as the individual knows, in advance, that his own vote, standing alone, cannot effectively block a proposal, he will not be motivated to exploit others for his own uniquely differential benefit. If a proposal is presented for a vote that embodies net benefits for him, he will tend to accept it, even if under a rule of full unanimity, he would be tempted to block the same issue. Under relative unanimity, it seems probable that a sufficient number of individuals would behave nonstrategically to allow collective decisions on public goods to be reached. Interestingly, under relative unanimity we might predict that proposals embodying symmetry in solution would, on occasion, be adopted unanimously, whereas the same proposals, under full unanimity as the voting rule, would be rejected. This suggests that Wicksell’s purpose in partially relaxing the unanimity rule was not that of allowing for the overruling of a recalcitrant or “nonsocial” minority. Instead the purpose was that of modifying the conditions for choice for each member of the group in a way that eliminates from serious consideration the possibility of securing uniquely discriminatory benefits.

The Unanimity Rule and Pareto Optimality

The opportunities for bargaining, for strategic behavior, under the rule of unanimity, or relative unanimity, arise only for inframarginal proposals supplying-financing public goods. To relate our discussion of individual choice behavior in large groups operating under a unanimity rule to that of the earlier two-person trading model, we must assume that the public good or service can be provided in continuously variable quantities and that proposals will be made which allow for such continuous variation. On inframarginal units, net taxpayers’ surplus arises, and this provides the scope for bargaining behavior. The final distribution of the gains among separate persons will depend, in part, on the order of presentation of proposals. There is nothing in the institution of unanimity to determine the distribution of these gains analogous to the working of markets. As the margin is approached, the net surplus tends to be squeezed out, and at the margin itself no gains-from-trade remain. The number of proposals that can secure relatively unanimous approval is continually reduced as the margin is approached, and, at the last stage, only
one proposal for distributing the costs of an incremental addition to the quantity of a public good (given the manner of distribution of net gains over inframarginal units) can secure genuine unanimity. When the Pareto conditions are satisfied, by definition, no proposal for change can secure the consent of all parties. The converse also applies. From any position that does not satisfy the Pareto conditions, there must exist changes that can secure the approval of all persons in the group, bargaining difficulties aside.

The necessary relaxation of the unanimity rule in the strict sense and its replacement by the rule of relative unanimity or qualified majority involves some cost in efficiency. Strictly speaking, there is no assurance that the Pareto frontier will be attained under any rule short of full unanimity if side payments in money are not allowed. Proposals which must secure the support of only five-sixths of the total number of persons in a group may be adopted and still be nonoptimal, and departures from Pareto positions may take place under such a rule.

Only a partial escape from this dilemma seems possible. If the rule for making decisions is separated from the observer’s evaluation of collective decision-making, it becomes possible to rank all such decisions in terms of their efficiency. As shown above, some departure from strict unanimity is necessary to reduce the scope for strategic bargaining behavior by the individual and to insure that group decisions do, in fact, get made. Once the rule for decision-making is chosen, however, the relative efficiency of different collective outcomes can be measured in terms of the percentage of total membership that agrees. If, under some relative unanimity or qualified majority rule (or even under simple-majority rule) a proposal receives unanimous support of all parties, the observer can label the move as “efficient” in the full Pareto sense. In this way, given any decision rule, he can array various voting outcomes in terms of the percentage of votes cast in their favor. The proportion of positive votes becomes an acceptable criterion for the efficiency of separate proposals.

The Unanimity Rule and Real-World Institutions

Knut Wicksell produced an escape from the free-rider dilemma inherent in the large-number, public-goods interdependence. If the rule of unanimity should be applied, even in a relative or qualified sense, public goods will tend to be supplied efficiently. Analytically, this Wicksellian contribution provides a major step toward the development of a theory of the demand and the supply of public goods and services. In terms of the institutions through which choices are made in the real world, however, more relevant theory is yet required. To some extent, the Wicksellian contribution serves much the same function here as the economist’s assumption of perfect competition in the theory of private-goods demand and supply. There is a major difference between the two devices, however, and this must be recognized. Again to an extent, something approaching the descriptive meaning of perfect competition can be shown to emerge from the interaction of individuals engaged in private market processes. Rarely will Wicksellian choice-making institutions emerge naturally from the rational decisions of individuals, even when we consider the appropriate stages of constitutional choice. Real-world observations suggest that considerations other than simple efficiency must loom large in dictating the rules for collective decision-making. The Wicksellian device is helpful, however, in establishing a benchmark from which possible sacrifices of first-order economic efficiency can be measured, at least conceptually. Subsequent chapters will explore some of the issues involved in developing a theory of public goods that seems better for explaining real-world events.

Bibliographical Appendix

In his fundamental contribution to the theory of public finance, Knut Wicksell noted the predicted failure of voluntary individual behavior to generate efficient outcomes in the presence of public-goods phenomena. [
Finanztheoretische Untersuchungen (Jena: Gustav Fischer, 1896). A major portion of this essay is translated as: “A New Principle of Just Taxation,” and included in
Classics in the Theory of Public Finance, edited by R. A. Musgrave and A. T. Peacock (London: Macmillan, 1958), pp. 72-118.] In his later model, Erik Lindahl was perhaps less perceptive than Wicksell concerning the difficulties in any voluntaristic solution. [
Die Gerechtigkeit des Besteuerung (Lund, 1919). A major portion of this essay is translated as: “Just Taxation—A Positive Solution,” and included in
Classics in the Theory of Public Finance, pp. 168-76.] Later essays by Lindahl should also be noted [“Some Controversial Questions in the Theory of Taxation,” originally written in German and published in 1928, and published in translation and included in,
Classics in the Theory of Public Finance, pp. 214-32; also, “Tax Principles and Tax Policy,”
International Economic Papers, No. 10 (London: Macmillan, 1959), pp. 7-23].

In his early critical review of Lindahl’s model, R. A. Musgrave stressed the failure of the voluntary-exchange mechanism [“The Voluntary Exchange Theory of Public Economy,”
Quarterly Journal of Economics, LIII (February 1939), 213-37]. In his later, and somewhat more favorable, treatment of the Lindahl model, Musgrave emphasized the difficulties in getting individuals to reveal their true preferences in voluntary exchanges involving genuinely public goods [
The Theory of Public Finance (New York: McGraw-Hill, 1959), Ch. 4]. This aspect of the problem was also stressed by Paul A. Samuelson in his initial paper [“The Pure Theory of Public Expenditure,”
Review of Economics and Statistics, XXXVI (November 1954), 387-89]. Some of the ambiguities involved in the whole “free-rider” notion are sensed by Ansel M. Sharp and Donald R. Escarraz although they do not fully succeed in removing them [“A Reconsideration of the Price or Exchange Theory of Public Finance,”
Southern Economic Journal, XXXI (October 1964), 132-39].

The analysis of the free-rider problem was clarified by Otto A. Davis and Andrew Whinston, especially as concerns the failure of individuals to reveal their preferences [“Some Foundations of Public Expenditure Theory” (Mimeographed, Carnegie Institute of Technology, November 1961)]. Mancur Olson discussed the free-rider problem in some detail and extended the analysis to the problem of the viability of organizations [
The Logic of Collective Action (Cambridge: Harvard University Press, 1965)]. Olson and Richard Zeckhauser have also applied essentially the same analysis to international sharing problems [“An Economic Theory of Alliances,”
Review of Economics and Statistics, XLVII (August 1966), 266-79]. J. F. Besson has applied the analysis to issues of centralized versus decentralized planning, and he has also provided a good general summary of existing public-goods theory [“Centralisation et decentralisation: Le problème des biens collectifs,”
Revue Economique (No. 4, 1966), 560-602]. Albert Breton has also attempted to relate the theory of public goods to the theory of collective decision-making [“A Theory of Demand for Public Goods,”
Canadian Journal of Economics and Political Science, XXXII (November 1966), 455-67].

The problems of deriving norms for behavior in a voluntaristic ethics are closely related to those discussed in this chapter. M. A. Singer provided a modern discussion of the generalization principle [
Generalization in Ethics (New York: Alfred A. Knopf, 1961)]. The necessity of distinguishing between the generalization argument and the argument in favor of establishing general rules was pointed out by Neil A. Dorman [“The Refutation of the Generalization Argument,”
Ethics, LXXIV (January 1964), 150-54]. Some of the specific relationships between the ethical discussion and the economic one were treated, along with the necessity of distinguishing behavior in the small-number and the large-number cases, in my own paper [“Ethical Rules, Expected Values, and Large Numbers,”
Ethics, LXXVI (October 1965), 1-13].

The free-rider problem in public-goods theory is an example of what may properly be called a “large-number prisoners’ dilemma,” a problem that is pervasive in many areas of economic theory. For a good general discussion of the prisoners’ dilemma in the two-person model, the treatment by R. Duncan Luce and Howard Raiffa is recommended [
Games and Decisions (New York: John Wiley and Sons, 1957), pp. 94-101]. Much of the analysis concerned with the competitiveness of alternative industrial structures is devoted, directly or indirectly, to the same issue. The “theory of chiseling” on cartel agreements is essentially the “theory of the free rider” in reverse. [For an interesting discussion on the former, see G. Warren Nutter, “Duopoly, Oligopoly, and Emerging Competition,”
Southern Economic Journal, XXX (April 1964), 342-52).]

In two separate works, independently and jointly written, I have examined some of the implications of Wicksell’s proposals for institutional reform, notably his proposal for the rule of unanimity or near-unanimity [“Positive Economics, Welfare Economics, and Political Economy,” included in
Fiscal Theory and Political Economy (Chapel Hill: University of North Carolina Press, 1960), pp. 105-24, and the book written jointly with Gordon Tullock,
The Calculus of Consent (Ann Arbor: University of Michigan Press, 1962)].