The Demand and Supply of Public Goods
By James M. Buchanan
First Pub. Date
1968
Publisher
Indianapolis, IN: Liberty Fund, Inc.
Pub. Date
1999
Comments
First published in 1968 by Rand McNally & Company. Foreword by Geoffrey Brennan.
Copyright
The text of this edition is copyright ©: 1999 Liberty Fund, Inc. Picture of James M. Buchanan: File photo detail, courtesy Liberty Fund, Inc. James M. Buchanan, Charlottesville, Virginia, 1964.
- Foreword
- Ch. 1, A Methodological Introduction
- Ch. 2, Simple Exchange in a World of Equals
- Ch. 3, Simple Exchange in a World of Unequals
- Ch. 4, Pure and Impure Public Goods
- Ch. 5, Many Private Goods, Many Persons
- Ch. 7, The Publicness of Political Decisions
- Ch. 8, The Institutions of Fiscal Choice
- Ch. 9, Which Goods Should Be Public
- Ch. 10, Toward a Positive Theory of Public Finance
- Supplementary Reading Materials
 The Publicness of Political Decisions
The Publicness of Political Decisions
Introduction
Individuals demand certain goods and services that they supply publicly through political rather than market organization. These goods enter as arguments in individual utility functions, and a theory of demand can be derived. The modern theory of public goods has been largely devoted to such derivation. If interpreted properly, this theory provides predictive hypotheses concerning the outcomes of collective decision processes under certain highly restrictive assumptions. At the same time and in a more familiar context, the theory provides allocative or efficiency norms for the provision of these goods and services. In either usage, the theory applies to
any goods and services that are, for any reason, organized publicly. The technical characteristics of goods may and should influence the decisions on the appropriate organization of supply. This will be discussed more fully in Chapter 9. But the theory, as such, is appropriate to
public organization for any good or service.
This “publicness” in the organization of supply requires further discussion. To the extent that decisions are made politically, regardless of their specific content, there are “public-goods” elements present. It is in this context that the theoretical exercises of Chapter 6 provide a useful bridge between the analysis of private demand and that of “public supply.” In a world without a private-good numeraire, all decisions are necessarily public, whether these be concerned with the supply of particular goods or with rules that govern behavior. For this reason, in Chapter 6, quantities of public goods, issues and even candidates for elective office were often used interchangeably as the objects of collective choice; deliberate ambiguity was employed as a means of stressing the identity of the analysis in each case.
Public goods and private goods are indistinguishable as they enter individual utility functions. Individuals want different things. With privately supplied goods, market exchange facilitates individual adjustments to preferred quantities, within limits imposed by resource constraints, in total and in individually divisible shares. The outcome of a private-goods trade is a changed allocation or distribution of commodities among individual traders. The situation is quite different with public goods. The outcome of “exchange,” through some collective decision rule, is “agreement” on the same quantity of good, to be shared by all traders and
commonly consumed. There is no individual quantity adjustment. Individual adjustments must be made in “prices,” not in quantities, if the outcomes are to be classified as efficient in the standard sense.
Earlier chapters have shown that the required differentiation in the structure of prices for public goods may emerge as a result of “trades” among individuals when the number in the trading process remains small. Adjustments in the cost-shares measured in money, a perfectly divisible numeraire, will take place until agreement is reached on a quantity of the common good. When the number of persons is large, the autonomous emergence of such a “pricing” pattern cannot be predicted. In the real world where public goods are shared by large numbers of persons, the “pricing structure” must be agreed on in much the same manner as the quantity of good to be provided. This aspect of public-goods theory has been relatively neglected, perhaps largely because the emphasis has been placed on the derivation of efficiency norms rather than on the processes of collective agreement. In the strictly formal sense, the satisfaction of the necessary conditions for efficiency or optimality implies the presence of a structure of marginal prices. When this level of formalism is dropped and the process of reaching agreement among persons is analyzed, the problem becomes two-dimensional at best. Agreement must be reached on the quantity of the public goods to be supplied and on the sharing of the cost, both in total and at the margin, among separate members of the group.
To an individual, these are clearly related decisions. The amount of any public good that he will prefer will depend on the share in its cost that he individually must bear. Most persons would prefer a larger quantity the lower their own share in the payment. This is a simple application of the first law of demand which, when combined with commonality in consumption, provides the basis for the free-rider problem already discussed in Chapter 5. It is misleading, however, in the large-number model to attempt to derive a structure of individual shares from an analysis of offers and counter-offers. Conceptually, this sort of analysis is possible, because individuals can make such offers differentially in the private-goods or money numeraire, which is fully divisible among persons, but it is relevant only when very small numbers are involved. And, in these cases, strategic elements of behavior tend to be unduly stressed. A different analytical framework is required for large-number settings.
At one level of analysis, there seems nothing public about the individual’s own tax-share. Different individuals may be subjected to different tax-prices; there seems to be no common sharing in the ordinary sense. However, this approach overlooks the necessary publicness of the decision over the sharing of public-goods cost among persons. Individuals can express their preferences, through some voting scheme, only on tax-sharing
schemes or
structures. They can vote on a whole set of tax-prices or tax-shares, total and marginal, and this set necessarily includes not only their own liability but those for all other members of the group. It is impossible for an individual to “offer” his own desired payment, independent of payments to be made by all others. It is in this sense that alternative sharing schemes are “purely public.” Each person must adjust his own behavior to the
same scheme of payment; the fact that this is chosen and enforced politically insures its publicness, despite the fact that individual payments are to be made in a fully divisible numeraire. The scheme, or schemes when alternatives are considered, may contain widely differing shares for different persons. Descriptively, any alternative here is a vector with characteristics of individual tax shares as components.
The General Nature of Tax-Sharing Schemes
As the small-number trading models as well as the more formal mathematical ones suggest, “price” differentials among separate demanders of public goods must reflect differentials in preferences, even down to the individual level, if the necessary conditions for optimality are to be satisfied. In large-number situations appropriate to real-world fiscal decisions, the fine discrimination dictated by such conditions can hardly be achieved. Not only would great difficulties be encountered in reaching agreement, but the large number of sharing possibilities cannot even be considered. Alternatives presented for political decision must be severely limited. This suggests that, almost necessarily, the sharing arrangements presented will reflect objectively determinate criteria for “price differentials.” At best, therefore, alternative tax-sharing vectors among which choice is possible will subdivide individuals into broad groups, classified not in terms of their privately expressed public-goods preferences but in terms of general characteristics that are presumably related to such preferences in some representative or average sense.
General criteria will be employed to establish classificatory systems, and the satisfaction of the necessary conditions for efficiency in public-goods supply will be approached only to the extent that actual preferences of individuals are arrayed roughly in accord with these general criteria.
One common and almost universally used general classification relies on the relative economic positions of individuals (families) as defined by appropriate income-wealth measures. Personal income or wealth is taken as an externally selected criterion for imposing relative tax-shares, and the more sophisticated fiscal theorists have supported this procedure on the ground that this criterion does correspond roughly to relative demands for public goods. This relationship is likely to hold only for general-benefit goods, and only to the extent that they exhibit positive income elasticities of demand. This seems to be one general presumption underlying modern fiscal structures.
Any general classification in which tax liabilities are related to variables that individuals can control creates difficulties. Individuals will attempt to reduce their relative shares in the costs of public goods by shifting their position as defined by the basis of the sharing scheme. Such shifting can take place only within limits, however, and the underlying classification in accordance with income-wealth criteria is also presumed to remain relevant. Given a general income-wealth criterion, more explicit definition of the relative shares will depend on the predicted shifts in individual behavior, and, this aside, specific allocation of shares will arouse disagreement, but this aspect of the problem need not be discussed at this point.
Within an income-wealth classification and given some specific rate structure, an individual’s tax-share will finally be determined, not by his own particular demand for or evaluation of the public good (or public-goods bundles) but by his position in the private economy after he has made his tax-base adjustments. He is never in a position where he can react to the “offers” of others in any direct sense. He cannot express his public-goods preferences explicitly. He can, however, express these indirectly through the political process. He can, directly or through his participation (or nonparticipation) in electing representatives, approve or disapprove various tax-share vectors and various proposals for public-spending programs. Preferring high levels of public-goods supply, he will vote for larger spending projects and, perhaps, for tax-sharing arrangements that place higher shares on his own income-wealth class. As the analysis below will indicate, however, there is much less likelihood that individuals will positively approve increases in their own tax-shares.
A Simplified Two-Person Model
To analyze collective agreement on both public-goods quantity and tax-sharing arrangements, it will once again be helpful to resort to the simple two-person model because much of the analysis carries over into the relevant many-person models. We want to examine the behavior of two persons, High and Low, as they adjust to two public variables: first, the quantity of public goods, and, secondly, the specific tax-sharing scheme to finance this quantity. For simplicity in presentation, we shall assume initially that all tax-sharing alternatives to be considered embody marginal tax-prices to individual taxpayers that are constant over quantity.
The individuals are assumed to be independently classified by their relative economic positions. High stands high by income-wealth criteria and Low stands low. The single public good is assumed to be beneficial to both and to have a positive income elasticity of demand for both.
 |
| Figure 7.1 |
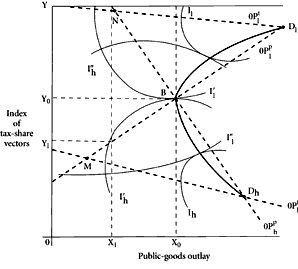
The situation can be shown in Figure 7.1, which is related to the constructions introduced in Chapter 6. The quantity of the public good is shown along the horizontal axis, and is measured in dollars worth of outlay. This allows us to incorporate the costs of the good in this variable. We assume that the unit cost of the good is fixed. Tax-share vectors are arrayed along the vertical axis. To accomplish this, some index must be selected. Given the various simplifications imposed on this model, the index can be a relatively simple one measuring “share progressivity” in the tax structure. At the origin, we locate that tax-sharing scheme which assigns to Low 100 per cent of the total cost of the public good, regardless of the amount to be financed. At
Y, the other extreme, we locate the tax-sharing plan that assigns 100 per cent of the cost of the public good to High, regardless of the amount to be financed. All possible sharing schemes are arrayed between these limits.
The preferences of the two individuals can be mapped onto Figure 7.1 in the standard fashion. Low’s most desired combination is likely to be located at some point,
D
l, where there is a large quantity of the good supplied but where this is almost wholly financed by taxes levied on High. The most preferred combination for High is less predictable, but presumably at some point,
D
h, he will desire a relatively large quantity of the public good that is financed through a tax-sharing scheme that keeps his own share relatively low. The probable presence of certain equity considerations in High’s utility function insures that his optimally preferred position will lie somewhere above the horizontal axis.
Following the construction of Chapter 6, lines of optima may be drawn in Figure 7.1. The shapes of these under our set of assumptions seem predictable. Low’s line of public-goods optima will take the general shape shown by 0
P
lp. This indicates the amount of public good which Low will optimally prefer at all possible tax-share arrangements arrayed in accordance with the share progressivity index. Clearly, this line will be positively sloped, indicating that Low will desire a larger quantity of the public good as his own share in the cost is reduced and High’s share increased. It also seems reasonable to expect that this line of optima for Low will have some positive intercept on the vertical axis. This indicates that, at some level of the tax-share index, he will prefer to forego completely the benefits of the public good because his own payment becomes too large, and competing demands on his resources make him unwilling to pay for the public good at these levels of taxation.
High’s comparable public-goods line of optima will tend to be negatively sloped, but the absolute value of the slope will perhaps be somewhat higher than that for Low. The line of optima may not intersect the vertical axis below
Y, suggesting that High may be willing to finance a certain quantity of the good even if he is forced to bear the full costs. As his cost-shares fall below this level, he will prefer larger amounts of the good, but, as the absolute slope indicates, he will be less sensitive than Low to his share in the payment.
Lines of tax-share optima can also be derived from the indifference contours and these are drawn in as 0
P
lt and 0
P
ht on Figure 7.1. Low will clearly prefer a tax-sharing scheme that will at all levels of provision impose the predominant share of the cost on High. High may accept larger shares of public-goods costs at lower budgetary levels than at higher ones. To indicate this possibility his line of tax-share optima is drawn with a slight downslope.
If one of the two persons should be assigned the decision authority over tax shares and the other over public-goods quantity, the resulting equilibrium would be either at
M or at
N. In either case, the result would be extremely inefficient and would allow for a relatively small total outlay.
Significant differences are to be noted in the relative positions of the two lines of optima in each case, and this is important for the theory of collective agreement. Note that the lines of optima for the two persons, with respect to the preferred quantities of public goods, intersect at
B. There is no comparable intersection of the tax-share lines of optima. At the tax-sharing scheme,
Y0, both parties will agree on a most desired public outlay. This defines a Pareto-optimal solution, given the limitations imposed on this model. Note that, at
B, the public-goods lines of optima intersect and also cut the contract locus. All points on this locus are, of course, Pareto-optimal in the larger sense. These include the extreme limits,
D
h and
D
l, one of which would prevail should all decision power be vested in one man. The position shown at
B, however, seems to embody “reasonableness” characteristics for a solution not possessed by other positions on the locus. If the two persons commence at the origin, where none of the public good is being provided,
B seems to be a reasonable outcome of negotiations on both variables, since it is the maximum public-goods quantity upon which the two persons can reach agreement given a unique tax-sharing scheme. This scheme reflects the precise structure of “price differentials” to bring public-goods preferences into agreement.
Note that at
B, the lines of tax-share optima remain widely separated. There is no comparable agreement on this variable subject to collective choice. The reason is that this variable is almost purely distributional; an increase in one person’s tax-share reduces that of the other. At any level of outlay, either person would prefer to secure that outlay at a lower rather than at a higher cost to himself.
It is interesting to examine Wicksell’s unanimity proposals within this framework. He suggested that for each expenditure proposal advanced, an array of tax-sharing schemes should be considered, and unless at least one such scheme could secure unanimous approval the expenditure should not be made. Suppose that, in terms of Figure 7.1, an initial proposal is made to spend an amount
X1 on the public good. Tax-sharing schemes are presented along with this spending proposal. In this context, any tax-sharing scheme falling between
Y1 and
Y may be approved by both parties, ignoring purely strategic behavior. For an amount of spending,
X1, High would, if necessary, finance the whole cost. Similarly, Low would, if necessary, pay a major share as indicated in the scheme at
Y1. Agreement becomes possible, on some tax-sharing arrangement
and on the spending proposal, anywhere between these limits. Having adopted this initial spending proposal, suppose that a further proposal is made in the second round to expand the level of outlay incrementally. Agreement remains possible, with many alternative sharing schemes on such increments, but the multiplicity of possible arrangements diminishes rapidly as
X0 is approached. At the margin, at
X0, only one sharing scheme can command the approval of both parties, that shown by
Y0. For all proposals to expand spending beyond
X0, no sharing scheme will command the approval of both parties.
The position shown at
B is, therefore, the uniquely determinate Wicksellian solution to the problem of public-goods allocation and tax-sharing, given the restrictions of our model. These restrictions include constant marginal tax-shares over quantity. This particular restriction can be relaxed; the construction remains useful, but only if income-effect feedbacks on individual preferences are neglected. In this case, the solution is determinate in terms of
marginal tax-shares and public-goods outlay. Any number of sharing schemes over inframarginal units becomes possible. If income-effects are taken into consideration, no such determinacy can be represented diagrammatically.
It may also be useful to compare, in a general way, these results with those suggested in the familiar set of efficiency norms advanced by Samuelson. These are stated as marginal conditions that must be satisfied for optimality and do not include explicit reference to total conditions. A uniquely determinate result is attained only by resort to an externally derived “social welfare function” which does, of course, specify the final distribution of “welfare.” Almost by definition, the necessary marginal conditions are satisfied at any point on the contract locus between
D
h and
D
l in Figure 7.1. Samuelson then calls upon the social welfare function to select from among these points. He does not deal with the processes of reaching agreement on specific outcomes.
Extension to Three-Person Models
Only within two-person limits is the analysis of collective agreement on the two fiscal variables wholly free of complexities which would tend to obscure the essential elements under discussion if introduced too early. These complexities arise in three-person models and are compounded as the analysis is extended to larger groups.
As shown in the exercises of Chapter 6, no problem arises in adding utility-function mappings for other persons onto a construction similar to Figure 7.1,
provided that the variables are treated as purely collective or public goods. We have argued above that all individuals must adjust to a common tax-sharing arrangement or tax structure and that, despite the divisibility of individual tax-shares, these structures can best be analyzed as if they are public goods (or public bads). This creates no problems in a purely formal sense, but serious difficulties arise in any analysis of a group decision process.
These stem from attempts to array tax-share vectors on the vertical axis in such a way that, as between this variable and the public-goods variable measured along the horizontal axis, individual preference mappings exhibit the standard properties of convexity. This task of arraying tax-share vectors is greatly simplified in the two-person case. Here individual shares in cost must be strictly related, one to the other. Since the total must sum to unity, an increase in the share of one person can only mean a decrease,
pari passu, in the share of the second. The utility functions of both persons defined on the two variables, public-goods outlay and an index of tax-share vectors, can be expected to exhibit the standard properties.
With three persons, no such one-to-one correspondence among individual shares can exist; an increase in the tax-share for one person may be accompanied by a decrease in the share of
either one or
both of the other two persons. For any one person, it is possible to array tax-share vectors in such a way that a utility mapping will exhibit convexity. But it will not be possible, in the general case, that this same index will allow for convexity in the mappings for all three persons.
To resolve this difficulty let us first place one additional restriction on the set of tax-sharing arrangements to be considered. Plausibly, we impose the requirement that cost-shares shall not be related inversely to the external criterion that is used to classify persons or groups. If income is used here, this restriction suggests only that those persons with lower incomes shall not be required to contribute cost-shares higher than persons standing above them on the independent income scale, regardless of relative preferences for public goods. In any real-world context, no tax-sharing arrangement is likely to violate this additional restriction, although, in a formal sense, particular configurations of public-goods preferences may make adherence to this restriction produce inefficient results
per se. These latter possibilities have, however, already been ruled out by our earlier assumption that for each person there is a positive income elasticity of demand for the public good. The practical effect of this restriction is that the alternative standing lowest on the tax-vector index is defined by equal sharing among all persons in the group.
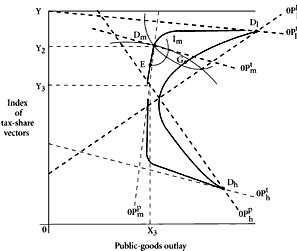
(a) Symmetry with respect to median income With this restriction, we can now examine the three-person model first under an extremely helpful, and not implausible, simplifying assumption that further limits the set of tax-sharing arrangements to be considered as alternatives. We assume that the share of the median-income person in the three-person group shall remain unchanged over all possible arrangements. In an earlier work, I have referred to this characteristic as symmetry with respect to the median-income person. An arithmetical example will clarify the precise meaning here. As suggested, the lowest point on the index will represent a vector indicating equal tax-shares, or vector (1/3, 1/3, 1/3) . As we move up the index or scale, the share of the low-income man decreases and the share of the high-income man increases, but the share of the median man remains unchanged at one-third. The highest point on the index is represented by the vector (0, 1/3, 2/3) . This simplification, in effect, converts the three-person model into the two-person one.
 |
| Figure 7.2 |
Geometrical representation is in Figure 7.2. The situations of two of the three persons, Low and High, are substantially identical with those in Figure 7.1. For the third man, Median, only one of the two dimensions is intensively relevant. Since he will, under our assumption, pay one-third of the cost of the public good, regardless of the distribution of the remaining two-thirds among his two colleagues, he will tend to prefer approximately the same level of public-goods outlay at all tax-sharing schemes. If we allow him to exhibit some concern for distributional consequences, we may locate his most preferred single combination at
D
m, somewhat nearer to the upper bound of the tax-vector set than to the lower. At best, however, we should expect his indifference contours to be elongated, and his public-goods line of optima to be steep, as shown by 0
P
mp. If Median is concerned exclusively with his own share, there will be no tax-share line of optima, but, again, if we allow for some distributional motivation, this line may lie roughly as shown by 0
P
mt in Figure 7.2.
With this setting, what can be predicted to emerge as a result of collective-choice processes? The contract surface takes the shape enclosed by the heavy solid lines of Figure 7.2. Let us initially consider the predicted outcome when the two variables are decided upon separately and by simple-majority voting rules. As the analysis of Chapter 6 showed, the solution in this case is given by the intersection of middle lines of optima, shown at
D
m. In the configuration as drawn, this process of decision effectively allows Median to dictate the community outcome for both variables. He attains his “peak” level of preference. At this solution, there will be widespread disagreement concerning the most preferred public-goods outlay. With a tax-sharing scheme presented at
Y2, High will prefer a much smaller budget, while Low will prefer a much larger one. Wicksellian unanimity is far from being achieved in the shift to this solution.
Consider now a modification in the decision rules that allows for simultaneous consideration of both variables, again under simple-majority voting rules. Suppose that the solution at
D
m has been provisionally stabilized and that a coalition between High and Low forms and proposes a shift to
G. Clearly, both men will benefit, Low accepting a somewhat larger share in cost in exchange for High’s agreement for an expanded public-goods outlay. This position, at
G, will not, of course, be majority-stable. Cyclical shifts can take place within and upon the bounds of the contract surface. Certain plausible restrictions can be placed on such moves in the particular configuration of Figure 7.2. Median is primarily if not exclusively interested in shifting horizontally; he is relatively indifferent as between vertical alternatives, at any level. Accordingly, High is much more likely to succeed in forming a new coalition with Median to organize shifts away from
G. If he does so, some shift to a new position, say
E, will take place. This will be somewhat closer to a Wicksellian solution in that the disagreement over public-goods quantity will be substantially less intense at this point than at
D
m or at
G. However, this position,
E, is not majority-stable either, and further shifts can be made.
A similar analysis could, of course, be carried out no matter where the lines of optima should be located for Median with respect to those for the other two persons.
The construction suggests that majority-decision rules, whether these involve separate consideration of issues or simultaneous consideration, will not produce solutions that will be accepted by all parties, save in some constitutional sense of acquiescence. The result produced by majority voting may, as in the above examples, qualify as a Pareto-optimal position once it is attained, but it cannot be
attained Pareto-optimally. Distributional elements will necessarily be present in the decision process. These are, of course, likely to be omnipresent in real-world fiscal choices and to this extent the model is highly realistic, but it will be useful to examine the Wicksellian unanimity rule as an alternative in this particular submodel.
As drawn, there is no Wicksellian solution in the strictly marginal sense as discussed in connection with Figure 7.1. For public-goods outlay proposals up to
X3, there are many tax-sharing schemes that will be accepted. Beyond
X3, disagreement appears; Median objects to further outlay, and given the limits on the tax-sharing vectors imposed by our symmetry assumption, no further moves can be made with general consent. A proximate Wicksellian solution is, therefore, attainable at an outlay,
X3, and a tax-sharing scheme,
Y3.
(b) Lexicographic ordering Symmetry in share progressivity with respect to median income is unduly restrictive. Some attempt must be made to construct an index of tax-share vectors without this crutch. We propose to construct an index that will reflect a lexicographic ordering of the vectors. As before, we retain the restriction that the lowest vector on the scale will be that which indicates equal sharing among all members of the community. Above this, we first array all possible vectors in subsets classified Low’s share, in ascending order as this share falls. The vectors in each of these subsets will represent different means of residual sharing between Median and High. Within each of these subsets, we then array vectors in ascending order as Median’s share falls. This type of ordering can be extended to any number of persons and can include all possible tax-sharing schemes, given the initial restrictions imposed on all of the models.
An arithmetical illustration of this ordering will be helpful. Assume that a possible set of tax-share vectors to be ordered is:
(.1, .3, .6) (.2, .4, .4) (.1, .2, .7) (.1, .4, .5) (.2, .3, .5) (.1, .1, .8) (.2, .2, .6)
Arraying these along a vertical scale we get:
| g | (.1, .1, .8) |
| f | (.1, .2, .7) |
| e | (.1, .3, .6) |
| d | (.1, .4, .5) |
| c | (.2, .2, .6) |
| b | (.2, .3, .5) |
| a | (.2, .4, .4) |
This procedure generates a systematic ordering of all possible vectors, but it does not eliminate the convexity problem. Consider the limited array above. Note that Median pays a larger tax-share in both
d and
e than he does in
c, while High pays a lower tax-share in
d than he does in
c. For both Median and High, preference mappings will exhibit nonconvexity.
 |
| Figure 7.3 |
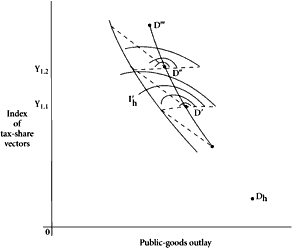
Figure 7.3 depicts the likely pattern of indifference contours for High. His optimally preferred combination is shown at
D
h, located roughly in the same position as before. Note, however, that local peaks will occur at
D‘,
D”, and
D‴. As abrupt shifts are made from one subset to another, High’s utility is increased, locally, despite the general decline in his utility as his position is moved northwestward. For example, at
D”, because of the shift of subset, he may be brought suddenly back to a level of utility equal to that attained on the contour
I‘. The public-goods line of optima for High will roughly follow the pattern shown by the dotted line on Figure 7.3. This lies within an area confined by the two solid lines, and the width of this area progressively widens as we move vertically up the figure. This is because of the greater range of distributional splits between Median and High as Low’s share is reduced.
 |
| Figure 7.4 |
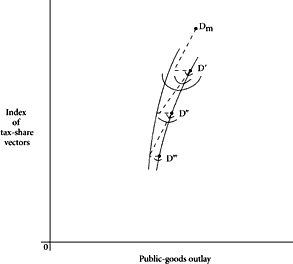
Figure 7.4 depicts, in similar way, the utility mapping for Median. As shifts are made between subsets classified by Low’s share, Median will also confront “cliffs,” and his preference surface will exhibit local peaks at
D‘,
D”, and
D‴. Because of the ordering scheme used, these local cliffs will be facing opposite to those of High. This can be noted in the arithmetical array. As a shift is made from
c to
d, Median’s share
increases despite the decrease in his minimal share as we shift up the scale. By contrast, High’s share
decreases, despite the increase in his maximum share as we move up the same scale.
 |
| Figure 7.5 |
The whole analysis is combined in Figure 7.5. As drawn, there is a broad range of possible intersections between the public-goods lines of optima for High and Median. Positions in the shaded area will not insure agreement between these two persons. But a position in this intersection does suggest that agreement may be produced by appropriately organized, and possibly minimal, changes in the tax-sharing arrangements. These can be of a localized sort and Low’s tax-share need not be modified. If Low’s line of public-goods optima cuts through this broad intersection, general agreement among all three parties seems possible. Some approximation to a Wicksellian solution can be realized in such cases.
Note that there is not likely to be agreement on tax-sharing schemes, even given a possible agreement on public-goods outlay. This conclusion resembles that reached in the earlier and simpler models. Also, if the two decisions, one on public-goods outlay and the other on the tax-sharing arrangement, should be taken separately and if majority rule prevails, the result may tend to be in the vicinity of
D
m, also suggested by the earlier models.
This model should not be treated with great respect for its helpfulness, but neither should its suggestiveness be wholly neglected. The complexities that arise in the analysis of agreement should not obscure the underlying need to analyze the agreement processes. The problem to be analyzed is surely present under some circumstances. Agreement must be reached on both of the variables and many more besides, and these surely contain “publicness” elements in that all members of the community must adjust to the result.
As additional persons are added to the model, the ordering becomes more difficult, although the lexicographic method can formally be used for any number. Geometrical representation becomes messy, but the essentials of the analysis are not changed. As additional public goods, rules or institutions are taken into account, the prospects for agreement tend to increase in the relative sense discussed in Chapter 6.
Perhaps the test of usefulness for the models of this chapter is the question: Are hypotheses implied that can be tested by observations? Conceptually, tests can be made to determine to what extent the real-world solutions meet Wicksellian criteria. If, given the budgetary level and the tax-sharing scheme in existence, there is observed to be widespread disagreement concerning budgetary size and if this disagreement tends to be inversely related to level of income, this would provide strong evidence that a solution approximated by
D
m is present. On the other hand, if the disagreement over budgetary size should be unrelated to income level, and if this disagreement should, in some relative sense, be minor, strong evidence is provided that some approximation to the Wicksellian results is achieved. Such evidence could never be conclusive, of course, because of the many alternative explanatory models that could be developed. It is worth recalling at this point that J. K. Galbraith, in his famous argument over the poverty of the public sector, implicitly assumed that the sustained budgetary position was of the sort depicted at
D
m on the figures. The tax-sharing arrangement in being was held to prevent majority approval for the expanded spending programs that he considered to be desirable. His remedy was fully consistent with the analysis of this chapter. He proposed a substantial downward shift in the scale of tax-sharing in order to achieve the required approval for larger spending programs.
Private Decisions and Public Goods
This chapter draws attention to an important element of individual participation in collective choice that tends to be neglected in the theory of public goods in the standard sense. This neglect is evidenced in earlier chapters of this book as well as in the works of other scholars. Individual demand for a public good is derived from a utility function that does not include arguments for the cost-shares or tax-shares to be paid by other members of the community. Conceptually, an individual marginal evaluation schedule (or demand schedule under the appropriately restricted assumptions) is related to tax-prices or tax-price offers. This schedule allows us to talk about the behavior of the individual in “voting for” or “voting against” particular spending proposals. In this analysis, it is acknowledged that individuals cannot privately select preferred outcomes and that these must be determined by some group decision rule. But the analysis does purport to explain individual participation in this process, and, in this elementary explanation, individual demands are related only to tax-prices or tax-price offers in the direct and explicit sense.
The neglected element is the “publicness” of the tax-share choice. The individual chooses public-goods quantities, not only in relation to the total and marginal tax-prices that he expects to be confronted with, but also in some relation to the whole tax-sharing scheme or arrangement which allocates tax-shares between himself and other members of the group. Introspective experiment can make the importance of this element clear. Consider your own possible participation in, say, a community referendum on a proposed public outlay for improvement in municipal park facilities. Suppose that your own share in the tax-cost is equivalent under two separate financing alternatives. Suppose, however, that one of these alternatives exempts all high-income persons from taxation while the other scheme exempts all low-income persons. It seems evident that you will have some definite preferences as between the two tax-sharing schemes, a preference which you are required to express if these alternatives are themselves presented for group choice.
The publicness of tax-sharing arrangements requires that the individual pay some attention to the whole structure of payments. Recognition of the possible influence of this element on his behavior should not, however, blind us to the primary significance of his own tax-share in determining his behavior pattern. The theory of public goods remains incomplete when this element is wholly neglected, but such neglect is justified in the preliminary stages of inquiry when the purpose is that of isolating the most important influence on the demand for public goods.
In choosing both a quantity of public goods and a tax-sharing scheme for financing this quantity, the individual participates in a collective decision process that he recognizes as such. He is choosing
for others as well as for himself. This very setting will tend to make him consider the relative positions of others. This situation may be compared with that faced by the individual in competitive market organization. In the latter, he does not explicitly recognize the indirect effect that his behavior will exert on others in the community. He tends to behave as if his actions exert no such influence. There is no explicit publicness in his choice calculus. The distinction between individual positions in these two situations provides the basis for some of the traditional socialist criticism of market order. The argument here, in summary, is that individuals, if forced to choose
for the group, will surely widen their range of consideration. An acknowledgement of
some difference in probable motivation for behavior in the two cases is not the same thing, however, as an acknowledgement of
categorical difference. If, in fact, individuals could be predicted to choose among “public” alternatives on the basis of their own versions of group rather than an individual interest, we could discard much of the theory of public goods and of welfare economics, and devote time exclusively to analyses of the sort contained in Chapters 7 and 8. Conflicts would arise to the extent that personal definitions of group interest differ, and utility functions of the standard variety simply would not exist.
Bibliographical Appendix
The geometrical constructions of Chapter 7 are derived, generally, from the works cited previously in connection with Chapter 6, primarily those of Duncan Black. For the particular applications to the simultaneous choice of public-goods outlay and tax-sharing schemes, the constructions for the two-person model closely parallel those presented by Leif Johansen [“Some Notes on the Lindahl Theory of Determination of Public Expenditures,”
International Economic Review, IV (September 1963), 346-58]. Figure 7.1, in the text, is substantially equivalent to Johansen’s Figure 3. Although Johansen does not extend his formal analysis beyond the two-person (two-group) model, some of his critical comments on the Lindahl model, generally, are also relevant to the discussion of this chapter. In his book [
Public Economics (Chicago: Rand McNally, 1965)], notably Chapter 6, Johansen’s geometrical construction is less detailed, although other comments are expanded beyond those in his paper.
Johansen’s point of departure is Erik Lindahl’s classic work [
Die Gerechtigkeit der Besteuerung (Lund, 1919), relevant portions of which are translated as: “Just Taxation—A Positive Solution,” and published in
Classics in the Theory of Public Finance, edited by R. A. Musgrave and A. T. Peacock (London: Macmillan, 1958), pp. 168-76]. Lindahl’s later papers are also relevant [“Some Controversial Questions in the Theory of Taxation,” as translated into English from the German and also published in
Classics in the Theory of Public Finance; also see, “Tax Principles and Tax Policy,”
International Economic Papers, No. 10 (London: Macmillan, 1959), pp. 7-23]. R. A. Musgrave summarizes the basic Lindahl contribution in his treatise [
The Theory of Public Finance (New York: McGraw-Hill, 1959), pp. 74-78]. In an earlier paper, Musgrave discussed the Lindahl theory in some detail [“The Voluntary Exchange Theory of Public Economy,”
Quarterly Journal of Economics, LIII (February 1938), 213-37]. A more recent and more exhaustive discussion of Lindahl’s contribution, along with consideration of possible criticisms, has been published by J. G. Head [“Lindahl’s Theory of the Budget,”
Finanzarchiv, Band 23, Heft 4 (October 1964), 422-54].
As several critics have noted, Lindahl’s theory suffers in its extension to the political decision process. It is in this respect that Wicksell’s seminal contribution seems superior. Wicksell was concerned with potentially applicable rules for making political choices on both public-goods outlay and on tax-sharing arrangements, and he did not develop his theory in an explicit two-person bargaining context.
Howard Bowen, in his early contribution to the modern theory, set the whole problem in a political context [“Voting and the Allocation of Resources,”
Quarterly Journal of Economics, LVIII (November 1943), 27-48, substantially reprinted in
Toward Social Economy (New York: Rinehart, 1948), pp. 172-98]. In his treatise, Musgrave devotes a chapter to “Budget Determination Through Voting” [
The Theory of Public Finance, Ch. 6]. Some parts of Musgrave’s discussion are directly relevant to the material covered in Chapter 7.
The most complete treatment of tax systems, considered as “public,” is contained in the work of Charles J. Goetz [
Tax Preferences in a Collective Decision-Making Context (Ph.D. dissertation, University of Virginia, 1965, available through University Microfilms, Ann Arbor, Michigan)]. Goetz examines group agreement on tax systems largely independent of group agreement on public-goods outlay, except as the recognition of underlying interdependence affects individual preference patterns. One portion of Goetz’s argument was published earlier [“A Variable-Tax Model of Intersectoral Allocation,”
Public Finance, XIX (No. 1, 1964), 29-41].
The possible differences between individual behavior in the choice of private goods and in the choice of public “goods” was stressed by William J. Baumol [
Welfare Economics and the Theory of the State (Cambridge: Harvard University Press, 1952; Second revised edition, 1965)]. In an early paper of my own, I attempted to examine these differences in some detail [“Individual Choice in Voting and the Market,”
Journal of Political Economy, LXII (August 1954), 334-43, reprinted in
Fiscal Theory and Political Economy (Chapel Hill: University of North Carolina Press, 1960), pp. 90-104]. The indirectness of the effects of individual behavior in the market process and its effect is discussed in the book by Robert A. Dahl and C. E. Lindblom [
Politics, Economics, and Welfare (New York: Harper, 1953)]. In a relatively recent paper, I have discussed some of the consequences for modern welfare economics arising out of the presumed categorical differences in individual behavior in voting and market processes [“Politics, Policy, and the Pigovian Margins,”
Economica, XXIX (February 1962), 17-28].
Recent works, in preliminary form, by Robert Dorfman and by Martin Shubik examine aspects of public-goods theory in a collective-choice setting [Dorfman, “General Equilibrium with Public Goods,” Working Paper No. 95, Institute of Business and Economic Research, University of California at Berkeley, June 1966; Shubik, “Notes on the Taxonomy of Problems Concerning Public Goods,” AD 633 546, Defense Documentation Center, April 1966]. Albert Breton has attempted to relate the theory of public goods to the theory of collective decision-making [“A Theory of the Demand for Public Goods,”
Canadian Journal of Economics and Political Science, XXXII (January 1966), 455-67].

